16.4: La energía de Gibbs
- Page ID
- 1927
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Habilidades para desarrollar
- La energía de Gibbs
- Definir la energía libre de Gibbs y describir su relación con la espontaneidad
- Calcular el cambio de energía libre para un proceso usando energías libres de formación para sus reactivos y productos
- Calcular el cambio de energía libre para un proceso usando las entalpías de formación y las entropías de sus reactivos y productos
- Explicar cómo la temperatura afecta la espontaneidad de algunos procesos
- Relacionar los cambios de energía libre estándar con las constantes de equilibrio.
Uno de los desafíos de usar la segunda ley de la termodinámica para determinar si un proceso es espontáneo es que debemos determinar el cambio de entropía del sistema y el cambio de entropía del entorno. Un enfoque alternativo que involucra una nueva propiedad termodinámica definida en términos de propiedades del sistema fue introducido a fines del siglo XIX por el matemático estadounidense Josiah Willard Gibbs. Esta nueva propiedad se llama el cambio de energía libre de Gibbs (G) (o simplemente energía libre) y se define en términos de la entalpía y la entropía de un sistema como sigue:
\[G=H−TS \label{1}\]
La energía libre es una función de estado y, a temperatura y presión constantes, el cambio de energía libre estándar (ΔG°) se puede expresar así:
\[ΔG=ΔH−TΔS \label{2}\]
(En aras de la simplicidad, el subíndice "sys" se omitirá de ahora en adelante). Podemos entender la relación entre esta propiedad del sistema y la espontaneidad de un proceso recordando la expresión de la segunda ley de la termodinámica derivada previamente:
\[ΔS_\ce{univ}=ΔS+\dfrac{q_\ce{surr}}{T} \label{3}\]
La primera ley requiere que qsurr = −qsys, y a presión constante qsys = ΔH, por eso esta expresión se puede reescribir como:
\[ΔS_\ce{univ}=ΔS−\dfrac{ΔH}{T} \label{4}\]
ΔH es el cambio de entalpía del sistema. Al multiplicar ambos lados de esta ecuación por −T y reorganizar, se obtiene lo siguiente:
\[−TΔS_\ce{univ}=ΔH−TΔS \label{5}\]
La comparación de esta ecuación con la anterior para el cambio de energía libre muestra la siguiente relación:
\[ΔG=−TΔS_\ce{univ} \label{6}\]
El cambio de energía libre es un indicador fiable de la espontaneidad de un proceso, es directamente relacionado con el indicador de espontaneidad previamente identificado, \(ΔS_{univ}\). La tabla \(\PageIndex{1}\) resume la relación entre la espontaneidad de un proceso y los signos aritméticos de estos indicadores.
| ΔSuniv > 0 | ΔG < 0 | espontáneo |
| ΔSuniv < 0 | ΔG > 0 | no espontáneo |
| ΔSuniv = 0 | ΔG = 0 | reversible (a equilibrio) |
Calculando el cambio de energía libre
La energía libre es una función de estado, por eso su valor depende solo de las condiciones de los estados inicial y final del sistema que han pasado por algún cambio. Un enfoque conveniente y común para el cálculo de los cambios de energía libre para las reacciones físicas y químicas es por el uso de las varias compilaciones disponibles de datos termodinámicos de estado estándar. Un método involucra el uso de las entalpías y las entropías estándar para calcular los cambios de energía libre estándar de acuerdo con la siguiente relación como se demuestra en el Ejemplo \(\PageIndex{1}\).
\[ ΔG°=ΔH°−TΔS° \label{7}\]
Ejemplo \(\PageIndex{1}\): La evaluación de ΔG°
Cambio de ΔH° y ΔS°: Utilice los datos de entalpía y entropía estándar de Tablas T1 o T2 para calcular el cambio de energía libre estándar para la vaporización del agua a temperatura ambiente (298 K). ¿Qué nos dice el valor calculado para ΔG ° sobre la espontaneidad de este proceso?
Solución
El proceso de interés es el siguiente:
\[\ce{H2O}(l)⟶\ce{H2O}(g) \label{\(\PageIndex{8}\)} \nonumber\]
El cambio estándar de energía libre se puede calcular utilizando la siguiente ecuación:
\[ΔG^\circ_{298}=ΔH°−TΔS° \label{\(\PageIndex{9}\)} \nonumber\]
De las Tablas T1 o T2, aquí están los datos:
| Sustancia | \(ΔH^\circ_\ce{f}\ce{(kJ/mol)}\) | \(S^\circ_{298}\textrm{(J/K⋅mol)}\) |
|---|---|---|
| H2O(l) | −286.83 | 70.0 |
| H2O(g) | −241.82 | 188.8 |
Combinando a 298 K:
\[ΔH°=ΔH^\circ_{298}=ΔH^\circ_\ce{f}(\ce{H2O}(g))−ΔH^\circ_\ce{f}(\ce{H2O}(l)) \nonumber\\
=\mathrm{[−241.82\: kJ−(−285.83)]\:kJ/mol=44.01\: kJ/mol} \nonumber\]
\[ΔS°=ΔS^\circ_{298}=S^\circ_{298}(\ce{H2O}(g))−S^\circ_{298}(\ce{H2O}(l)) \nonumber\\
=\mathrm{188.8\:J/mol⋅K−70.0\:J/K=118.8\:J/mol⋅K} \nonumber\]
\[ΔG°=ΔH°−TΔS° \nonumber\]
Convierta todo a kJ y calcule a 298 K:
\[ΔG^\circ_{298}=ΔH°−TΔS° \nonumber\]
\[\mathrm{=44.01\: kJ/mol−(298\: K×118.8\:J/mol⋅K)×\dfrac{1\: kJ}{1000\: J}} \nonumber\]
\[\mathrm{44.01\: kJ/mol−35.4\: kJ/mol=8.6\: kJ/mol} \nonumber\]
A 298 K (25 °C) \(ΔG^\circ_{298}>0\), por eso la ebullición no es espontánea (no espontánea).
Ejercicio \(\PageIndex{1}\)
Utilice los datos de la entalpía y la entropía estándar de las Tablas T1 o T2 para calcular el cambio de energía libre estándar para la reacción que se muestra aquí (298 K). ¿Qué nos dice el valor calculado para ΔG ° sobre la espontaneidad de este proceso?
\[\ce{C2H6}(g)⟶\ce{H2}(g)+\ce{C2H4}(g) \nonumber\]
Answer
\(ΔG^\circ_{298}=\mathrm{102.0\: kJ/mol}\); la reacción no es espontánea (no espontánea) a 25 °C.
Los cambios de energía libre también pueden usar la energía libre estándar de formación \((ΔG^\circ_\ce{f})\), para cada uno de los reactivos y productos involucrados en la reacción. La energía libre estándar de formación es el cambio de energía libre que acompaña a la formación de un mol de una sustancia a partir de sus elementos en sus estados estándar. Similar a las entalpías estándar de formación, \((ΔG^\circ_\ce{f})\) es por definición cero para las sustancias elementales en condiciones de estado estándar. El enfoque para calcular el cambio de energía libre para una reacción usando este enfoque es el mismo que se demostró anteriormente para los cambios de entalpía y entropía. Para la reacción
\[m\ce{A}+n\ce{B}⟶x\ce{C}+y\ce{D},\]
el cambio de energía libre estándar a temperatura ambiente se puede calcular así
\[ΔG^\circ_{298}=ΔG°=∑νΔG^\circ_{298}(\ce{products})−∑νΔG^\circ_{298}(\ce{reactants})\]
\[=[xΔG^\circ_\ce{f}(\ce{C})+yΔG^\circ_\ce{f}(\ce{D})]−[mΔG^\circ_\ce{f}(\ce{A})+nΔG^\circ_\ce{f}(\ce{B})].\]
Ejemplo \(\PageIndex{2}\): La calculación de \(ΔG^\circ_{298}\)
Considere la descomposición del óxido de mercurio (II) amarillo.
\[\ce{HgO}(s,\,\ce{yellow})⟶\ce{Hg}(l)+\dfrac{1}{2}\ce{O2}(g) \nonumber\]
Calcule el cambio de energía libre estándar a temperatura ambiente, \(ΔG^\circ_{298}7\), usando (a) las energías libres estándar de formación y (b) las entalpías estándar de formación y entropías estándar. ¿Los resultados indican que la reacción es espontánea o no espontánea en condiciones estándar?
Solución
Los datos requeridos están disponibles en las Tablas T1 o T2 y se muestran aquí.
| Compuesto | \(ΔG^\circ_\ce{f}\:\mathrm{(kJ/mol)}\) | \(ΔH^\circ_\ce{f}\:\mathrm{(kJ/mol)}\) | \(S^\circ_{298}\:\textrm{(J/K⋅mol)}\) |
|---|---|---|---|
| HgO (s, amarillo) | −58.43 | −90.46 | 71.13 |
| Hg(l) | 0 | 0 | 75.9 |
| O2(g) | 0 | 0 | 205.2 |
(a) Usando las energías libres de formación:
\[ΔG^\circ_{298}=∑νGS^\circ_{298}(\ce{products})−∑νΔG^\circ_{298}(\ce{reactants}) \nonumber\]
\[=\left[1ΔG^\circ_{298}\ce{Hg}(l)+\dfrac{1}{2}ΔG^\circ_{298}\ce{O2}(g)\right]−1ΔG^\circ_{298}\ce{HgO}(s,\,\ce{yellow}) \nonumber\]
\[\mathrm{=\left[1\:mol(0\: kJ/mol)+\dfrac{1}{2}mol(0\: kJ/mol)\right]−1\: mol(−58.43\: kJ/mol)=58.43\: kJ/mol} \nonumber\]
(b) Usando las entalpías y las entropías de formación:
\[ΔH^\circ_{298}=∑νΔH^\circ_{298}(\ce{products})−∑νΔH^\circ_{298}(\ce{reactants}) \nonumber\]
\[=\left[1ΔH^\circ_{298}\ce{Hg}(l)+\dfrac{1}{2}ΔH^\circ_{298}\ce{O2}(g)\right]−1ΔH^\circ_{298}\ce{HgO}(s,\,\ce{yellow}) \nonumber\]
\[\mathrm{=[1\: mol(0\: kJ/mol)+\dfrac{1}{2}mol(0\: kJ/mol)]−1\: mol(−90.46\: kJ/mol)=90.46\: kJ/mol} \nonumber\]
\[ΔS^\circ_{298}=∑νΔS^\circ_{298}(\ce{products})−∑νΔS^\circ_{298}(\ce{reactants}) \nonumber\]
\[=\left[1ΔS^\circ_{298}\ce{Hg}(l)+\dfrac{1}{2}ΔS^\circ_{298}\ce{O2}(g)\right]−1ΔS^\circ_{298}\ce{HgO}(s,\,\ce{yellow}) \nonumber\]
\[\mathrm{=\left[1\: mol(75.9\: J/mol\: K)+\dfrac{1}{2}mol(205.2\: J/mol\: K)\right]−1\: mol(71.13\: J/mol\: K)=107.4\: J/mol\: K} \nonumber\]
\[ΔG°=ΔH°−TΔS°=\mathrm{90.46\: kJ−298.15\: K×107.4\: J/K⋅mol×\dfrac{1\: kJ}{1000\: J}} \nonumber\]
\[ΔG°=\mathrm{(90.46−32.01)\:kJ/mol=58.45\: kJ/mol} \nonumber\]
Ambas formas de calcular el cambio de energía libre estándar a 25 °C nos dan el mismo valor numérico (a tres cifras significativas) y ambas predicen que el proceso es no espontáneo (no espontáneo) a temperatura ambiente.
Ejercicio \(\PageIndex{2}\)
Calcule ΔG° usando (a) las energías libres de formación y (b) las entalpías de formación y las entropías (Tablas T1 o T2). ¿Los resultados indican que la reacción es espontánea o no espontánea a 25 ° C?
\[\ce{C2H4}(g)⟶\ce{H2}(g)+\ce{C2H2}(g) \nonumber\]
Respuesta:
−141.5 kJ/mol, no espontánea
La dependencia de la espontaneidad en la temperatura
Como se demostró previamente en la sección de este capítulo sobre la entropía, la espontaneidad de un proceso puede depender de la temperatura del sistema. Las transiciones de fase, por ejemplo, se desarrollarán espontáneamente en una u otra dirección dependiendo de la temperatura de la sustancia en cuestión. Asimismo, algunas reacciones químicas también pueden exhibir espontaneidades dependientes de la temperatura. Para ilustrar este concepto, se considera la ecuación que relaciona el cambio de energía libre con los cambios de la entalpía y la entropía para el siguiente proceso:
\[ ΔG=ΔH−TΔS \]
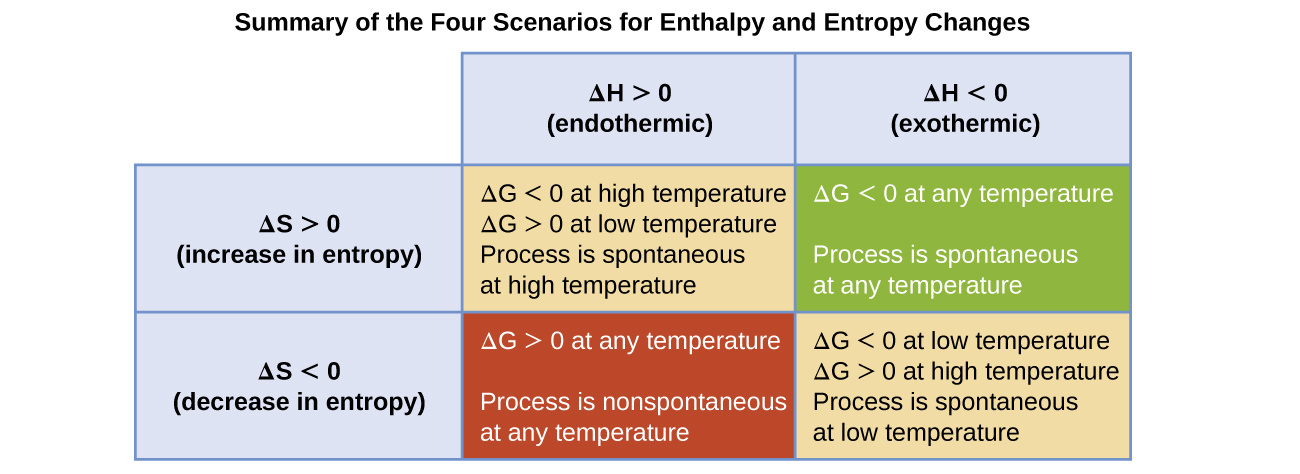
La espontaneidad de un proceso, mostrada por el signo aritmético de su cambio de energía libre, está determinada por los signos de los cambios de la entalpía y la entropía y, en algunos casos, la temperatura absoluta. Dado que T es la temperatura absoluta (kelvin), solo puede tener valores positivos. Por lo tanto, existen cuatro posibilidades con respecto a los signos de los cambios de la entalpía y la entropía:
- Ambos ΔH y ΔS son positivos. Esta condición describe un proceso endotérmico que involucra un aumento en la entropía del sistema. En este caso, ΔG será negativo si la magnitud del término TΔS es mayor que ΔH. Si el término TΔS es menor que ΔH, el cambio de energía libre será positivo. Este proceso es espontáneo a temperaturas altas y no espontáneo a temperaturas bajas.
- Ambos ΔH y ΔS son negativos. Esta condición describe un proceso exotérmico que involucra una disminución en la entropía del sistema. En este caso, ΔG será negativo si la magnitud del término TΔS es menor que ΔH. Si la magnitud del término TΔS es mayor que ΔH, el cambio de energía libre será positivo. Este proceso es espontáneo a temperaturas bajas y no espontáneo a temperaturas altas.
- ΔH es positivo y ΔS es negativo. Esta condición describe un proceso endotérmico que involuca una disminución en la entropía del sistema. En este caso, ΔG será positivo independientemente de la temperatura. Tal proceso no es espontáneo a todas las temperaturas.
- ΔH es negativo y ΔS es positivo. Esta condición describe un proceso exotérmico que involucra un aumento en la entropía del sistema. En este caso, ΔG será negativo independientemente de la temperatura. Tal proceso es espontáneo a todas las temperaturas.
Estos cuatro escenarios se resumen en la Figura \(\PageIndex{1}\).
Ejemplo \(\PageIndex{3}\): Predecir la dependencia de la espontaneidad en la temperatura
La combustión incompleta del carbono se describe usando la siguiente ecuación:
\[\ce{2C}(s)+\ce{O2}(g)⟶\ce{2CO}(g) \nonumber\]
¿Cómo depende la espontaneidad de este proceso en la temperatura?
Solución
Los procesos de combustión son exotérmicos (ΔH <0). Esta reacción en particular involucra un aumento en la entropía debido al aumento acompañante en la cantidad de especies gaseosas (una ganancia neta de un mol de gas, ΔS> 0). Por eso, la reacción es espontánea (ΔG <0) a todas las temperaturas.
Ejercicio \(\PageIndex{3}\)
Los calentadores populares de mano químicos producen calor mediante la oxidación del hierro con el aire:
¿Cómo depende la espontaneidad de este proceso de la temperatura?
Respuesta:
ΔH y ΔS son negativos; la reacción es espontánea a temperaturas bajas.
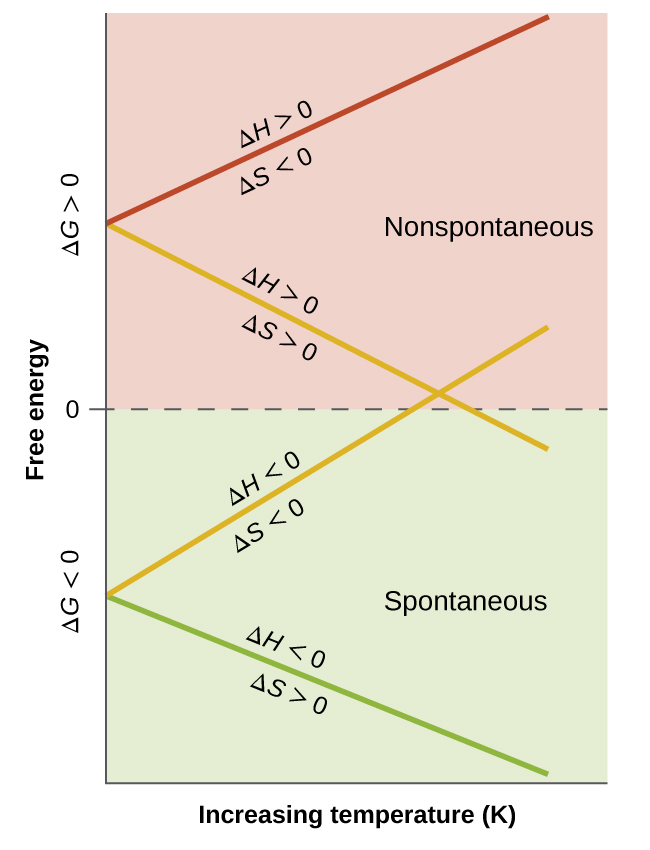
Al considerar las conclusiones hechas con respecto a la dependencia de la espontaneidad de la temperatura, es importante tener en cuenta lo que significan los términos "alta" y "baja". Dado que estos términos son adjetivos, las temperaturas en cuestión se consideran altas o bajas en relación con alguna temperatura de referencia. Un proceso que no es espontáneo a una temperatura, pero espontáneo a otra pasará por un cambio en la "espontaneidad" (como se refleja en su ΔG) a medida que varía la temperatura. Esto se ilustra claramente con una presentación gráfica de la ecuación de cambio de energía libre, en la que ΔG se representa en el eje y versus T en el eje x:
\[ΔG=ΔH−TΔS\]
\[y=b+mx\]
Este gráfico se muestra en la Figura \(\PageIndex{2}\). Un proceso cuyos cambios de entalpía y entropía son del mismo signo aritmético exhibirá una espontaneidad dependiente de la temperatura como se muestra en las dos líneas amarillas en el gráfico. Cada línea cruza de un dominio de espontaneidad (ΔG positivo o negativo) al otro a una temperatura que es característica del proceso en cuestión. Esta temperatura está representada por la intersección con el eje x de la línea, es decir, el valor de T para el cual ΔG es cero:
\[ΔG=0=ΔH−TΔS\]
\[T=\dfrac{ΔH}{ΔS}\]
Entonces, decir que un proceso es espontáneo a temperaturas “altas” o “bajas” significa que la temperatura está por encima o por debajo, respectivamente, de la temperatura a la que ΔG para el proceso es cero. Como se describió anteriormente, esta condición describe un sistema en equilibrio.
Ejemplo \(\PageIndex{4}\): Temperatura de equilibrio para una transición de fase
Como se explicó en el capítulo sobre los líquidos y los sólidos, el punto de ebullición de un líquido es la temperatura a la que sus fases sólida y líquida están en equilibrio (es decir, cuando la vaporización y la condensación ocurren a velocidades iguales). Utilice la información en las Tables T1 o T2 para estimar el punto de ebullición del agua.
Solución
El proceso de interés es el siguiente cambio de fase:
Cuando este proceso está en equilibrio, ΔG = 0, lo siguiente es cierto:
Usando los datos termodinámicos estándar de las Tablas T1 o T2,
ΔH°&=ΔH^\circ_\ce{f}(\ce{H2O}(g))−ΔH^\circ_\ce{f}(\ce{H2O}(l)) \nonumber\\
&=\mathrm{−241.82\: kJ/mol−(−285.83\: kJ/mol)=44.01\: kJ/mol} \nonumber
\end{align}\]
ΔS°&=ΔS^\circ_{298}(\ce{H2O}(g))−ΔS^\circ_{298}(\ce{H2O}(l)) \nonumber\\
&=\mathrm{188.8\: J/K⋅mol−70.0\: J/K⋅mol=118.8\: J/K⋅mol} \nonumber
\end{align}\]
El valor aceptado para el punto de ebullición normal del agua es 373.2 K (100.0 ° C), por eso este cálculo concuerda razonablemente. Tenga en cuenta que los valores de los datos de cambios de la entalpía y la entropía usados se derivaron de los datos estándar a 298 K (Tablas T1 o T2.). Si lo desea, puede obtener los resultados más precisos usando los cambios de la entalpía y la entropía determinados en (o al menos más cerca) del punto de ebullición real.
Ejercicio \(\PageIndex{4}\)
Use la informacion en las Tablas T1 o T2 para estimar el punto de ebullición de CS2.
Respuesta
313 K (valor aceptado de 319 K)
Energía libre y equilibrio
El cambio de energía libre de un proceso se puede ver como una medida de su fuerza impulsora. Un valor negativo para ΔG representa una fuerza impulsora finita para el proceso en la dirección de avance, mientras que un valor positivo representa una fuerza impulsora para el proceso en la dirección inversa. Cuando ΔG es cero, las fuerzas impulsoras de avance y la dirección inversa son iguales, por eso el proceso ocurre en ambas direcciones a la misma velocidad (el sistema está en equilibrio).
En el capítulo sobre el equilibrio, se introdujo el cociente de reacción, Q, como una medida conveniente del estado de un sistema de equilibrio. Recuerde que Q es el valor numérico de la expresión de acción de masas para el sistema, y se puede usar su valor para identificar la dirección en la que se desarrollará una reacción para lograr el equilibrio. Cuando Q es menor que la constante de equilibrio, K, la reacción procederá en la dirección de avance hasta que se alcance el equilibrio y Q = K. Por el contrario, si Q> K, el proceso procederá en la dirección inversa hasta que se alcance el equilibrio.
El cambio de energía libre para un proceso que ocurre con reactivos y productos presentes en condiciones no estándar, ΔG, está relacionado con el cambio de energía libre estándar, ΔG°, de acuerdo con esta ecuación:
R es la constante de gas (8.314 J/K mol), T es el kelvin o temperatura absoluta y Q es el cociente de reacción. Podemos usar esta ecuación para predecir la espontaneidad de un proceso bajo cualquier conjunto de condiciones, como se ilustra en el Ejemplo \(\PageIndex{1}\).
Ejemplo \(\PageIndex{5}\): Cálculo de ΔG en condiciones no estándar
¿Cuál es el cambio de energía libre para el proceso que se muestra aquí en las condiciones especificadas?
T = 25 °C, \(P_{\ce{N2}}=\mathrm{0.870\: atm}\), \(P_{\ce{H2}}=\mathrm{0.250\: atm}\), and \(P_{\ce{NH3}}=\mathrm{12.9\: atm}\)
Solución
La ecuación que relaciona el cambio de energía libre con el cambio de energía libre estándar y el cociente de reacción se puede usar directamente:
ΔG&=ΔG°+RT\ln Q=\mathrm{33.0\:\dfrac{kJ}{mol}+\left(8.314\:\dfrac{J}{mol\: K}×298\: K×\ln\dfrac{(0.250^3)×0.870}{12.9^2}\right)}\\
&=\mathrm{9680\:\dfrac{J}{mol}\:or\: 9.68\: kJ/mol}
\end{align}\]
Dado que el valor calculado para ΔG es positivo, la reacción no es espontánea en estas condiciones.
Ejercicio \(\PageIndex{5}\)
Calcule el cambio de energía libre para esta misma reacción a 875 °C en una mezcla de 5.00 L que contiene 0.100 moles de cada gas. ¿Es la reacción espontánea en estas condiciones?
Respuesta: ΔG = −47 kJ; sí
\[0=ΔG°+RT\ln K \hspace{40px} \textrm{(at equilibrium)}\]
Esta forma de la ecuación proporciona un vínculo útil entre estas dos propiedades termodinámicas esenciales y se puede usar para derivar las constantes de equilibrio a partir de los cambios de energía libre estándar y viceversa. Las relaciones entre los cambios de energía libre estándar y las constantes de equilibrio se resumen en la Tabla \(\PageIndex{1}\).
| K | ΔG° | Comentarios |
|---|---|---|
| < 1 | > 0 | Los reactivos son mas abundantes a equilibrio. |
| = 1 | = 0 | Los reactivos y productos son igualmente abundantes a equilibrio. |
| > 1 | < 0 | Los productos son mas abundantes a equilibrio. |
Ejemplo \(\PageIndex{6}\): La constante de equilibrio usando el cambio de energía libre estándar
Dado que las energías libres estándar de formación de Ag+(aq), Cl−(aq) y AgCl(s) son 77.1 kJ/mol, −131.2 kJ/mol y −109.8 kJ / mol, respectivamente, calcule el producto de solubilidad , Ksp, para AgCl.
Solución
La reacción de interés es la siguiente:
El cambio de energía libre estándar para esta reacción se calcula primero usando las energías libres de formación estándar para sus reactivos y productos:
\[ΔG°=ΔG^\circ_{298}=[ΔG^\circ_\ce{f}(\ce{Ag+}(aq))+ΔG^\circ_\ce{f}(\ce{Cl-}(aq))]−[ΔG^\circ_\ce{f}(\ce{AgCl}(s))]\]
La constante de equilibrio para la reacción se puede entonces derivar de su cambio de energía libre estándar:
K_\ce{sp}&=e^{−\dfrac{ΔG°}{RT}}=\exp\left(−\dfrac{ΔG°}{RT}\right)
=\mathrm{\exp\left(−\dfrac{55.7×10^3\:J/mol}{8.314\:J/mol⋅K×298.15\:K}\right)}\\
&=\mathrm{\exp(−22.470)=e^{−22.470}=1.74×10^{−10}}
\end{align}\]
Ejercicio \(\PageIndex{6}\)
Use los datos termodinámicos dados en las Tablas T1 o T2 para calcular la constante de equilibrio para la disociación del tetróxido de dinitrógeno a 25 °C.
\[\ce{NO}_{2(g)} \rightleftharpoons \ce{N_2O}_{4(g)}\]
Respuesta:K = 6.9
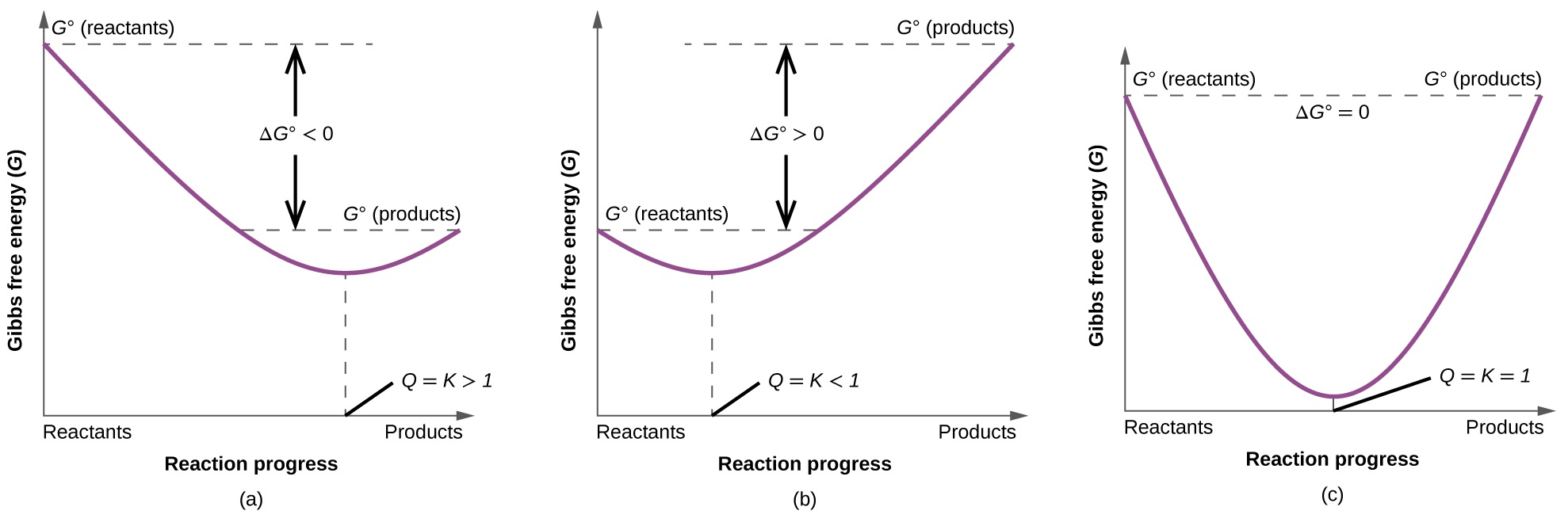
Para ilustrar aún más la relación entre estos dos conceptos termodinámicos esenciales, considere la observación de que las reacciones proceden espontáneamente en una dirección que finalmente establece el equilibrio. Como se puede mostrarse al graficar el cambio de energía libre frente a la extensión de la reacción (por ejemplo, como se refleja en el valor de Q), el equilibrio se establece cuando la energía libre del sistema se minimiza (Figura \(\PageIndex{3}\) ). Si un sistema está presente con los reactivos y los productos presentes en cantidades fuera de equilibrio (Q ≠ K), la reacción procederá espontáneamente en la dirección necesaria para establecer el equilibrio.
Resumen
La energía libre de Gibbs (G) es una función de estado definida con respecto a las cantidades del sistema únicamente y se puede usar para predecir la espontaneidad de un proceso. Un valor negativo para ΔG indica un proceso espontáneo; un ΔG positivo indica un proceso no espontáneo; y un valor de cero para ΔG indica que el sistema está en equilibrio. Son posibles varios enfoques para el cálculo de los cambios de energía libre.
Ecuaciones Clave
- ΔG = ΔH − TΔS
- ΔG = ΔG° + RT ln Q
- ΔG° = −RT ln K
Glosario
- Cambio de energía libre de Gibbs (G)
- propiedad termodinámica definida en términos de la entalpía y la entropía del sistema; todos los procesos espontáneos involucran una disminución de G
- cambio de energía libre estándar (ΔG °)
- cambio en la energía libre para un proceso que ocurre en condiciones estándar (1 bar de presión para gases, 1 M de concentración para soluciones)
- energía libre estándar de formación \((ΔG^\circ_\ce{f})\)
- cambio en la energía libre que acompaña la formación de un mol de sustancia a partir de sus elementos en sus estados estándar
Contribuyentes
Paul Flowers (Universidad de Carolina del Norte - Pembroke), Klaus Theopold (Universidad de Delaware) y Richard Langley (Stephen F. Austin Universidad del Estado) con autores contribuyentes. Contenido del libro de texto producido por la Universidad de OpenStax tiene licencia de Atribución de Creative Commons Licencia 4.0 licencia. Descarge gratis en http://cnx.org/contents/85abf193-2bd...a7ac8df6@9.110)."
Ana Martinez (amartinez02@saintmarys.edu) contribuyó a la traducción de este texto.


