5.7: Problemas

1. Supongamos que usa una dilución en serie para preparar 100 mL cada uno de una serie de estándares con concentraciones de\(1.00 \times10^{-5}\)\(1.00 \times10^{-4}\),\(1.00 \times10^{-3}\), y\(1.00 \times10^{-2}\) M a partir de una solución madre de 0.100 M. Calcule la incertidumbre para cada solución usando una propagación de incertidumbre, y compárela con la incertidumbre si prepara cada solución como una dilución única de la solución madre. Encontrará tolerancias para diferentes tipos de cristalería volumétrica y pipetas digitales en el Cuadro 4.2.1 y el Cuadro 4.2.2. Supongamos que la incertidumbre en la molaridad de la solución madre es ±0.0002.

2. Tres determinaciones replicadas de S _total para una solución estándar que es 10.0 ppm en analito dan valores de 0.163, 0.157 y 0.161 (unidades arbitrarias). La señal para el reactivo en blanco es 0.002. Calcular la concentración de analito en una muestra con una señal de 0.118.

3. Una muestra de 10.00 g que contiene un analito se transfiere a un matraz aforado de 250 ml y se diluye a volumen. Cuando una alícuota de 10.00 mL de la solución resultante se diluye a 25.00 mL da una señal de 0.235 (unidades arbitrarias). Una segunda porción de 10.00 mL de la solución se agrega con 10.00 mL de una solución estándar de 1.00-ppm del analito y se diluye a 25.00 mL. La señal para la muestra con picos es 0.502. Calcular el porcentaje en peso de analito en la muestra original.

4. Una muestra de 50.00 mL que contiene un analito da una señal de 11.5 (unidades arbitrarias). Una segunda alícuota de 50 mL de la muestra, a la que se le añade 1.00 mL de una solución estándar de 10.0-ppm del analito, da una señal de 23.1. ¿Cuál es la concentración del analito en la muestra original?

5. Una curva de calibración de adiciones estándar basada en la Ecuación 5.3.10 se coloca\(S_{spike} \times (V_o + V_{std})\) en el eje y y\(C_{std} \times V_{std}\) en el eje x. Derivar ecuaciones para la pendiente y la intercepción y y explicar cómo se puede determinar la cantidad de analito en una muestra a partir de la curva de calibración. Además, explique claramente por qué no se puede trazar el _pico S en el eje y y\(C_{std} \times \{V_{std}/(V_o + V_{std})\}\) en el eje x.

6. Una muestra estándar contiene 10.0 mg/L de analito y 15.0 mg/L de estándar interno. El análisis de la muestra da señales para el analito y el estándar interno de 0.155 y 0.233 (unidades arbitrarias), respectivamente. Se agrega suficiente patrón interno a una muestra para hacer su concentración 15.0 mg/L, el análisis de la muestra arroja señales para el analito y el estándar interno de 0.274 y 0.198, respectivamente. Reporte la concentración del analito en la muestra.

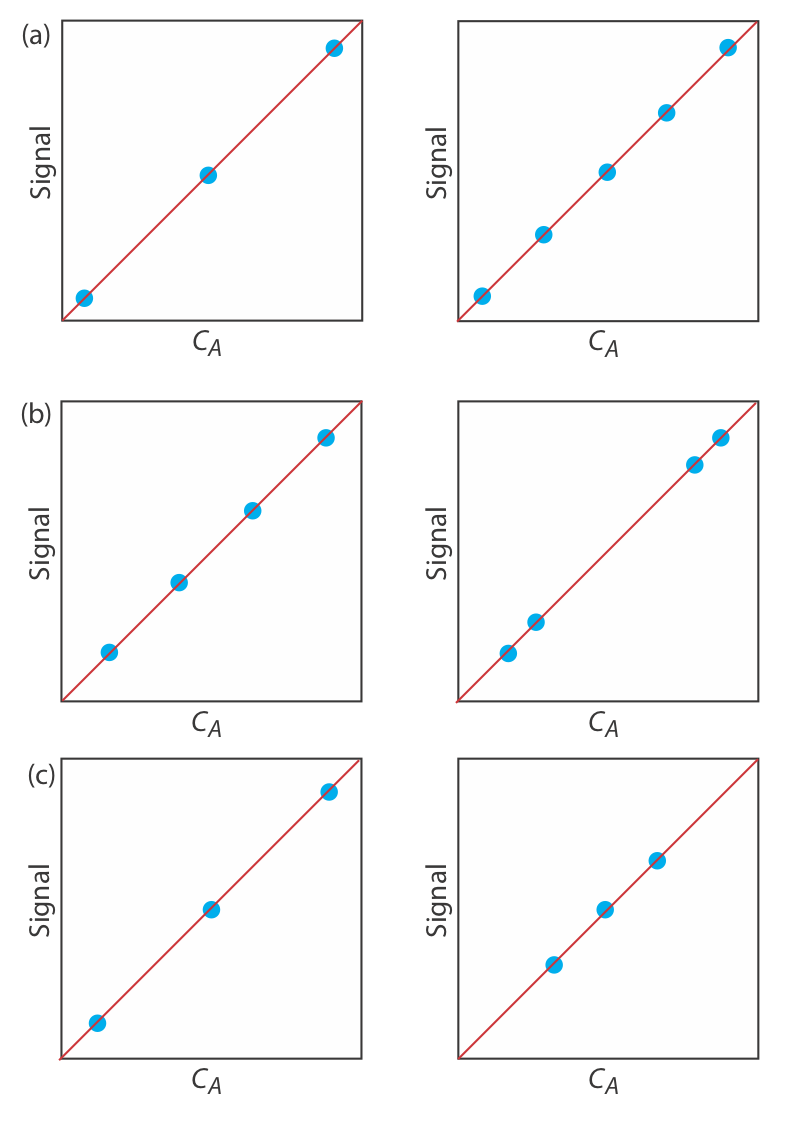
7. Para cada uno de los pares de curvas de calibración que se muestran a continuación, seleccione la curva de calibración que utilice el conjunto de estándares más apropiado. Explica brevemente los motivos de tus selecciones. Las escalas para el eje x y el eje y son las mismas para cada par.

8. Los siguientes datos son para una serie de estándares externos de Cd ^{2 +} tamponados a un pH de 4.6.

[Cd ^2+] (nM)	15.4	30.4	44.9	59.0	72.7	86.0
\(S_{spike}\)(nA)	4.8	11.4	18.2	26.6	32.3	37.7

(a) Utilizar un análisis de regresión lineal para determinar la ecuación para la curva de calibración y reportar intervalos de confianza para la pendiente y la intercepción y.

b) Construir una parcela de los residuos y comentar su significación.

A un pH de 3.7 se registraron los siguientes datos para el mismo conjunto de estándares externos.

[Cd ^2+] (nM)	15.4	30.4	44.9	59.0	72.7	86.0
\(S_{spike}\)(nA)	15.0	42.7	58.5	77.0	101	118

(c) ¿Cuánto más o menos sensible es este método al pH más bajo?

(d) Una sola muestra es tamponada a un pH de 3.7 y analizada para cadmio, produciendo una señal de 66.3 nA. Reportar la concentración de Cd ^{2 +} en la muestra y su intervalo de confianza del 95%.

Los datos en este problema son de Wojciechowski, M.; Balcerzak, J. Anal. Chim. Acta 1991, 249, 433—445.

9. Para determinar la concentración de analito en una muestra, se realiza una adición estándar. Se analiza una porción de 5.00-mL de muestra y luego se agregan espigas sucesivas de 0.10 mL de un estándar de 600.0 ppb del analito, analizando después de cada espiga. En la siguiente tabla se muestran los resultados de este análisis.

\(V_{spike}\)(mL)	0.00	0.10	0.20	0.30
\(S_{total}\)(unidades arbitrarias)	15.0	42.7	58.5	77.0

Construir una curva de calibración de adiciones estándar apropiada y usar un análisis de regresión lineal para determinar la concentración de analito en la muestra original y su intervalo de confianza del 95%.

10. Troost y Olavsesn investigaron la aplicación de una estandarización interna al análisis cuantitativo de hidrocarburos aromáticos polinucleares. Se obtuvieron los siguientes resultados para el análisis de fenantreno utilizando fenantreno marcado isotópicamente como patrón interno. Cada solución se analizó dos veces.

\(C_A/C_{IS}\)	0.50	1.25	2.00	3.00	4.00
\(S_A/S_{IS}\)	0.514 0.522	0.993 1.024	1.486 1.471	2.044 2.080	2.342 2.550

(a) Determinar la ecuación para la curva de calibración utilizando una regresión lineal, y reportar intervalos de confianza para la pendiente y la intercepción y. Promedio de las señales replicadas para cada estándar antes de completar el análisis de regresión lineal.

(b) Con base en sus resultados explique por qué los autores concluyeron que la estandarización interna era inapropiada.

Los datos en este problema son de Troost, J. R.; Olavesen, E. Y. Anal. Chem. 1996, 68, 708—711.

11. En el Capítulo 4.6. se utilizó una prueba t pareada para comparar dos métodos analíticos que se utilizaron para analizar independientemente una serie de muestras de composición variable. Un enfoque alternativo es graficar los resultados para un método versus los resultados para el otro método. Si los dos métodos arrojan resultados idénticos, entonces la parcela debe tener una pendiente esperada,\(\beta_1\), de 1.00 y una interseccion y esperada,\(\beta_0\), de 0.0. Podemos usar una prueba t para comparar la pendiente y la intercepción y de una regresión lineal a los valores esperados. El estadístico de prueba apropiado para la intercepción y se encuentra reordenando la Ecuación 5.4.10.

\[t_{exp} = \frac {|\beta_0 - b_0|} {s_{b_0}} = \frac {|b_0|} {s_{b_0}} \nonumber\]

Reordenando la Ecuación 5.4.9 da el estadístico de prueba para la pendiente.

\[t_{exp} = \frac {|\beta_1 - b_1} {s_{b_1}} = \frac {|b_1|} {s_{b_1}} \nonumber\]

Reevaluar los datos del Problema 25 del Capítulo 4 usando el mismo nivel de significancia que en el problema original.

Aunque este es un enfoque común para comparar dos métodos analíticos, sí viola uno de los requisitos para una regresión lineal no ponderada, que los errores indeterminados afectan a y solo. Debido a que los errores indeterminados afectan a ambos métodos analíticos, el resultado de una regresión lineal no ponderada es sesgado. Más específicamente, la regresión subestima la pendiente, b ₁, y sobreestima la intercepción y, b ₀. Podemos minimizar el efecto de este sesgo colocando el método analítico más preciso en el eje x, usando más muestras para aumentar los grados de libertad y usando muestras que cubren uniformemente el rango de concentraciones.

Para mayor información, véase Miller, J. C.; Miller, J. N. Statistics for Analytical Chemistry, 3a ed. Ellis Horwood PTR Prentice-Hall: Nueva York, 1993. Se encuentran enfoques alternativos en Hartman, C.; Smeyers-Verbeke, J.; Penninckx, W.; Massart, D. L. Anal. Chim. Acta 1997, 338, 19—40, y Zwanziger, H. W.; Sarbu, C. Anal. Chem. 1998, 70, 1277—1280.

12. Considere los siguientes tres conjuntos de datos, cada uno de los cuales da valores de y para los mismos valores de x.

x	y 1	y 2	y 3
10.00	8.04	9.14	7.46
8.00	6.95	8.14	6.77
13.00	7.58	8.74	12.74
9.00	8.81	8.77	7.11
11.00	8.33	9.26	7.81
14.00	9.96	8.10	8.84
6.00	7.24	6.13	6.08
4.00	4.26	3.10	5.39
12.00	10.84	9.13	8.15
7.00	4.82	7.26	6.42
5.00	5.68	4.74	5.73

(a) Un análisis de regresión lineal no ponderada para los tres conjuntos de datos da resultados casi idénticos. A tres cifras significativas, cada conjunto de datos tiene una pendiente de 0.500 y una intercepción y de 3.00. Las desviaciones estándar en la pendiente y la intercepción y son 0.118 y 1.125 para cada conjunto de datos. Las tres desviaciones estándar sobre la regresión son 1.24. Con base en estos resultados para un análisis de regresión lineal, comente la similitud de los conjuntos de datos.

(b) Completar un análisis de regresión lineal para cada conjunto de datos y verificar que los resultados de la parte (a) sean correctos. Construya una gráfica residual para cada conjunto de datos. ¿Estas parcelas cambian tu conclusión de la parte (a)? Explique.

(c) Trace cada conjunto de datos junto con la línea de regresión y comente sus resultados.

d) El conjunto de datos 3 parece contener un valor atípico. Elimine el valor atípico aparente y reanalice los datos usando una regresión lineal. Comenta tu resultado.

(e) Comente brevemente la importancia de examinar visualmente sus datos.

Estos tres conjuntos de datos son tomados de Anscombe, F. J. “Gráficos en Análisis Estadístico”, Amer. Statis. 1973, 27, 17-21.

13. Fanke y sus compañeros evaluaron un método estándar de adiciones para una determinación voltamétrica de Tl. En la siguiente tabla se presenta un resumen de sus resultados.

ppm Tl agregado	Respuesta del instrumento (\(\mu\)A)
0.000	2.53	2.50	2.70	2.63	2.70	2.80	2.52
0.387	8.42	7.96	8.54	8.18	7.70	8.34	7.98
1.851	29.65	28.70	29.05	28.30	29.20	29.95	28.95
5.734	84.8	85.6	86.0	85.2	84.2	86.4	87.8

Utilice una regresión lineal ponderada para determinar la relación de estandarización de estos datos.

Los datos en este problema son de Franke, J. P.; de Zeeuw, R. A.; Hakkert, R. Anal. Chem. 1978, 50, 1374—1380.