13.2: Cinética química

Los primeros métodos analíticos basados en la cinética química, que aparecen por primera vez a finales del siglo XIX, aprovecharon la actividad catalítica de las enzimas. En un método típico de esa época, se añadió una enzima a una solución que contenía un sustrato adecuado y se monitoreó su reacción por un tiempo fijo. La actividad de la enzima se determinó por el cambio en la concentración del sustrato. También se utilizaron enzimas para el análisis cuantitativo de peróxido de hidrógeno y carbohidratos. El desarrollo de métodos cinéticos químicos continuó en la primera mitad del siglo XX con la introducción de catalizadores no enzimáticos y reacciones no catalíticas.

A pesar de la diversidad de métodos cinéticos químicos, para 1960 ya no eran de uso común. La principal limitación de su aceptación más amplia fue la susceptibilidad a errores significativos de variables incontroladas o mal controladas —la temperatura y el pH son dos de estos ejemplos— y la presencia de interferentes que activan o inhiben reacciones catalíticas. Para la década de 1980, las mejoras en los métodos de instrumentación y análisis de datos compensaron estas limitaciones, asegurando un mayor desarrollo de métodos cinéticos químicos de análisis [Pardue, H. L. Anal. Chim. Acta 1989, 216, 69—107].

Teoría y Práctica

Cada reacción química ocurre a una velocidad finita, lo que la convierte en un candidato potencial para un método de análisis cinético químico. Para ser efectiva, sin embargo, la reacción química debe cumplir tres condiciones necesarias: (1) la reacción no debe ocurrir demasiado rápido o demasiado lento; (2) debemos conocer la ley de velocidad de la reacción; y (3) debemos ser capaces de monitorear el cambio de concentración para al menos una especie. Echemos un vistazo más de cerca a cada uno de estos requisitos.

El material de esta sección asume cierta familiaridad con la cinética química, que forma parte de la mayoría de los cursos de química general. Para una revisión de las velocidades de reacción, las leyes de velocidad y las leyes de tasas integradas, consulte el material en el Apéndice 17.

Velocidad de reacción

La velocidad de reacción química —qué tan rápido cambian las concentraciones de reactivos y productos durante la reacción— debe ser lo suficientemente rápida como para que podamos completar el análisis en un tiempo razonable, pero también lo suficientemente lenta como para que la reacción no alcance el equilibrio mientras los reactivos están mezcla. Como límite práctico, no es fácil estudiar una reacción que alcanza el equilibrio en varios segundos sin la ayuda de un equipo especial para mezclar rápidamente los reactivos.

Consideraremos dos ejemplos de instrumentación para estudiar reacciones con cinética rápida más adelante en este capítulo.

Ley de tarifas

El segundo requisito es que debemos conocer la ley de velocidad de la reacción —la ecuación matemática que describe cómo las concentraciones de reactivos afectan la tasa— para el periodo en el que estamos realizando mediciones. Por ejemplo, la ley de velocidad para una reacción que es de primer orden en la concentración de un analito, A, es

\[\text { rate }=-\frac{d[A]}{d t}=k[A] \label{13.1}\]

donde k es la constante de velocidad de la reacción.

Debido a que la concentración de A disminuye durante las reacciones, d [A] es negativa. El signo menos en la Ecuación\ ref {13.1} hace que la tasa sea positiva. Si elegimos seguir un producto, P, entonces d [P] es positivo porque la concentración del producto aumenta a lo largo de la reacción. En este caso omitimos el signo menos.

Una ley de tasa integrada a menudo es una forma más útil de la ley de velocidad porque es una función de la concentración inicial del analito. Por ejemplo, la ley de tasa integrada para la Ecuación\ ref {13.1} es

\[\ln{[A]_t} = \ln{[A]_0} - kt \label{13.2}\]

o

\[[A]_{t}=[A]_{0} e^{-k t} \label{13.3}\]

donde [A] ₀ es la concentración inicial del analito y [A] _t es la concentración del analito en el tiempo t.

Desafortunadamente, la mayoría de las reacciones de interés analítico no siguen una simple ley de tasas. Consideremos, por ejemplo, la siguiente reacción entre un analito, A, y un reactivo, R, para formar un solo producto, P

\[A + R \rightleftharpoons P \nonumber\]

donde _kf es la constante de velocidad para la reacción directa, y k _r es la constante de velocidad para la reacción inversa. Si las reacciones hacia adelante y hacia atrás ocurren como pasos simples, entonces la ley de velocidad es

\[\text { rate }=-\frac{d[A]}{d t}=k_{f}[A][R]-k_{r}[P] \label{13.4}\]

El primer término, k _f [A] [R] da cuenta de la pérdida de A ya que reacciona con R para hacer P, y el segundo término, k _r [P] da cuenta de la formación de A como P se convierte de nuevo a A y a R.

Aunque conocemos la ley de velocidad de reacción, no existe una forma integrada simple que podamos usar para determinar la concentración inicial del analito. Podemos simplificar la Ecuación\ ref {13.4} restringiendo nuestras medidas al inicio de la reacción cuando la concentración de producto es insignificante.

Bajo estas condiciones podemos ignorar el segundo término en la Ecuación\ ref {13.4}, lo que simplifica a

\[\text { rate }=-\frac{d[A]}{d t}=k_{f}[A][R] \label{13.5}\]

La ley de tasa integrada para la Ecuación\ ref {13.5}, sin embargo, sigue siendo demasiado complicada para ser analíticamente útil. Podemos simplificar aún más la cinética haciendo más ajustes a las condiciones de reacción [Mottola, H. A. Anal. Chim. Acta 1993, 280, 279—287]. Por ejemplo, podemos asegurar una cinética de pseudo-primer orden mediante el uso de un gran exceso de R para que su concentración permanezca esencialmente constante durante el tiempo que monitoreamos la reacción. Bajo estas condiciones, la ecuación\ ref {13.5} simplifica a

\[\text { rate }=-\frac{d[A]}{d t}=k_{f}[A][R]_{0}=k^{\prime}[A] \label{13.6}\]

donde k ′ = k _f [R] ₀. La ley de tasa integrada para la Ecuación\ ref {13.6} entonces es

\[\ln{[A]_t} = \ln{[A]_0} - k’t \label{13.7}\]

o

\[[A]_{t}=[A]_{0} e^{-k^{\prime} t} \label{13.8}\]

Incluso puede ser posible ajustar las condiciones para que usemos la reacción bajo condiciones de orden pseudo-cero.

\[\text { rate }=-\frac{d[A]}{d t}=k_{f}[A]_{0}[R]_{0}=k^{\prime \prime} t \label{13.9}\]

\[[A]_{t}=[A]_{0}-k^{\prime \prime} t \label{13.10}\]

donde\(k^{\prime \prime}\) = k _f [A] ₀ [R] ₀.

Decir que la reacción es pseudo-de primer orden en A significa que la reacción se comporta como si fuera de primer orden en A y de orden cero en R a pesar de que las cinéticas subyacentes son más complicadas. Llamamos constante\(k^{\prime}\) de velocidad de pseudo-primer orden. Decir que una reacción es de orden pseudo-cero significa que la reacción se comporta como si fuera de orden cero en A y de orden cero en R aunque la cinética subyacente sea más complicada. Llamamos a\(k^{\prime \prime}\) la constante de tasa de pseudo-orden cero.

Monitoreo de la Reacción

El requisito final es que debemos ser capaces de monitorear el progreso de la reacción siguiendo el cambio de concentración para al menos una de sus especies. Qué especies elegimos monitorear no es importante: puede ser el analito, un reactivo que reacciona con el analito, o un producto. Por ejemplo, podemos determinar la concentración de fosfato haciéndola reaccionar primero con Mo (VI) para formar ácido 12-molibdofosfórico (12-MPA).

\[\mathrm{H}_{3} \mathrm{PO}_{4}(a q)+6 \mathrm{Mo}(\mathrm{VI})(a q) \longrightarrow 12-\mathrm{MPA}(a q)+9 \mathrm{H}^{+}(a q) \label{13.11}\]

A continuación, reducimos 12-MPA a azul de heteropolifosfomolibdeno, PMB. La tasa de formación de PMB se mide espectrofotométricamente, y es proporcional a la concentración de 12-MPA. La concentración de 12-MPA, a su vez, es proporcional a la concentración de fosfato [ver, por ejemplo, (a) Crouch, S. R.; Malmstadt, H. V. Anal. Chem. 1967, 39, 1084—1089; b) Crouch, S. R.; Malmstadt, H. V. Anal. Chem. 1967, 39, 1090—1093; c) Malmstadt, H. V.; Cordos, E. A.; Delaney, C. J. Anal. Chem. 1972, 44 (12), 26A—41A]. También podemos seguir espectrofotométricamente la reacción 13.11 monitoreando la formación del 12-MPA de color amarillo [Javier, A. C.; Crouch, S. R.; Malmstadt, H. V. Anal. Chem. 1969, 41, 239—243].

La reacción\ ref {13.11} está, por supuesto, desequilibrada; los hidrógenos adicionales en el lado derecho de la reacción provienen de los seis Mo (VI) que aparecen en el lado izquierdo de la reacción donde se cree que Mo (VI) está presente como el dímero de molibdato HMo ₂ O ₆ ⁺.

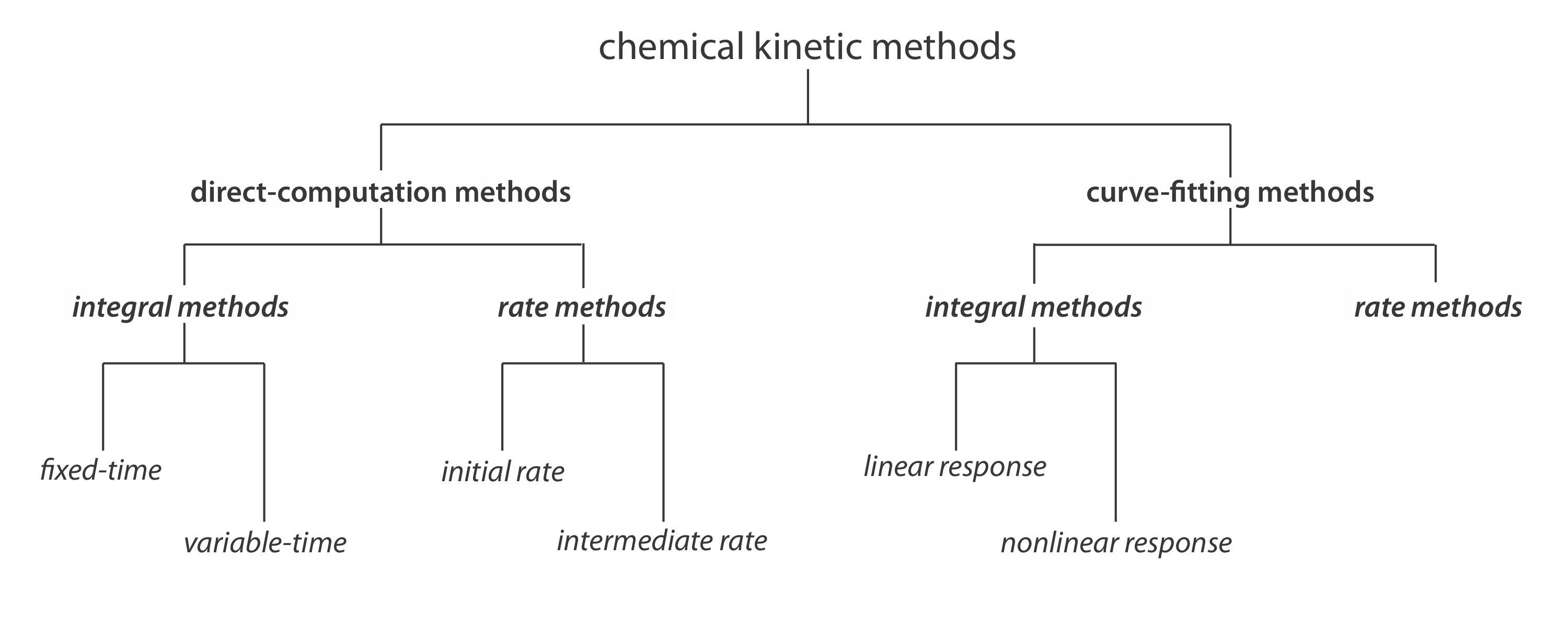
Clasificación de métodos cinéticos químicos

La Figura 13.2.1 proporciona un esquema útil para clasificar los métodos cinéticos químicos de análisis. Los métodos se dividen en dos amplias categorías: métodos de cálculo directo y métodos de ajuste de curvas. En un método de cálculo directo calculamos la concentración inicial del analito, [A] ₀, utilizando la ley de tasa apropiada. Por ejemplo, si la reacción es de primer orden en analito, podemos usar la Ecuación\ ref {13.2} para determinar [A] ₀ valores dados para k, t, y [A] _t. Con un método de ajuste de curvas, utilizamos la regresión para encontrar el mejor ajuste entre los datos, por ejemplo, [A] _t en función del tiempo y el modelo matemático conocido para la ley de tasas. Si la reacción es de primer orden en analito, entonces ajustamos la Ecuación\ ref {13.2} a los datos usando k y [A] ₀ como parámetros ajustables.

Figura 13.2.1 . Clasificación de métodos cinéticos químicos de análisis adaptados de Pardue, H. L. “Aspectos cinéticos de la química analítica”, Anal. Chim. Acta 1989, 216, 69—107.

Métodos Integrales de Tiempo Fijo de Computación Directa

Un método integral de cómputo directo utiliza la forma integrada de la ley tarifaria. En un método integral de tiempo fijo de un punto, por ejemplo, determinamos la concentración del analito en un solo tiempo y calculamos la concentración inicial del analito, [A] ₀, usando la ley de velocidad integrada apropiada. Para determinar la constante de velocidad de la reacción, k, realizamos un experimento separado usando una solución estándar de analito. Alternativamente, podemos determinar la concentración inicial del analito midiendo [A] _t para varios estándares que contienen concentraciones conocidas de analito y construir una curva de calibración.

Ejemplo 13.2.1

La concentración de nitrometano, CH ₃ NO ₂, se determina a partir de la cinética de su reacción de descomposición. En presencia de exceso de base la reacción es de pseudo-primer orden en nitrometano. Para una solución estándar de nitrometano 0.0100 M, la concentración de nitrometano después de 2.00 s es\(4.24 \times 10^{-4}\) M. Cuando se analiza una muestra que contiene una cantidad desconocida de nitrometano, la concentración de nitrometano restante después de 2.00 s es\(5.35 \times10^{-4}\) M. ¿Cuál es la concentración inicial de nitrometano en la muestra?

Solución

Primero, determinamos el valor para la constante de velocidad de pseudo-primer orden,\(k^{\prime}\). Usando la ecuación\ ref {13.7} y el resultado para el estándar, encontramos que su valor es

\[k^{\prime} = \frac {\ln{[A]_0} - \ln{[A]_t}} {t} = \frac {\ln{(0.0100)} - \ln{(4.24 \times 10^{-4})}} {2.00 \text{ s}} = 1.58 \text{ s}^{-1} \nonumber\]

A continuación utilizamos la Ecuación\ ref {13.8} para calcular la concentración inicial de nitrometano en la muestra.

\[[A]_0 = \frac {[A]_t} {e^{-k^{\prime}t}} = \frac {5.35 \times 10^{-4} \text{ M}} {e^{-(1.58 \text{ s}^{-1})(2.00 \text{ s})}} = 0.0126 \text{ M} \nonumber\]

La ecuación\ ref {13.7} y la ecuación\ ref {13.8} son leyes de velocidad integradas igualmente apropiadas para una reacción de pseudo-primer orden. La decisión de utilizar la Ecuación\ ref {13.7} para calcular\(k^{\prime}\) y la Ecuación\ ref {13.8} para calcular [A] ₀ es cuestión de conveniencia.

Ejercicio 13.2.1

En una determinación separada para nitrometano, una serie de estándares externos da las siguientes concentraciones de nitrometano después de una descomposición de 2.00 s bajo condiciones de pseudo-primer orden.

[CH 3 NO 2] 0 (M)	[CH 3 NO 2] t = 2.00 s (M)
0.0100	\(3.82 \times 10^{-4}\)
0.0200	\(8.19 \times 10^{-3}\)
0.0300	\(1.15 \times 10^{-3}\)
0.0400	\(1.65 \times 10^{-3}\)
0.0500	\(2.14 \times 10^{-3}\)
0.0600	\(2.53 \times 10^{-3}\)
0.0700	\(3.21 \times 10^{-3}\)
0.0800	\(3.35 \times 10^{-3}\)
0.0900	\(3.99 \times 10^{-3}\)
0.100	\(4.13 \times 10^{-3}\)

El análisis de una muestra en las mismas condiciones da una concentración de nitrometano de\(2.21 \times 10^{-3}\) M después de 2 s. ¿Cuál es la concentración inicial de nitrometano en la muestra?

Contestar

La curva de calibración y la ecuación de calibración para los estándares externos se muestran a continuación. Sustituyendo\(2.21 \times 10^{-3}\) M por [CH ₃ NO ₂] _{t = 2s} da [CH ₃ NO ₂] ₀ como\(5.21 \times 10^{-2}\) M.

En el Ejemplo 13.2.1 determinamos la concentración inicial del analito midiendo la cantidad de analito que no ha reaccionado. A veces es más conveniente medir la concentración de un reactivo que reacciona con el analito, o medir la concentración de uno de los productos de la reacción. Podemos usar un método integral de tiempo fijo de un punto si conocemos la estequiometría de la reacción. Por ejemplo, si medimos la concentración del producto, P, en la reacción

\[A+R \rightarrow P \nonumber\]

entonces la concentración del analito en el tiempo t es

\[[A]_{t}=[A]_{0}-[P]_{t} \label{13.12}\]

porque la estequiometría entre el analito y el producto es 1:1. Si la reacción es pseudo-de primer orden en A, entonces sustituyendo la Ecuación\ ref {13.12} en la Ecuación\ ref {13.7} da

\[\ln \left([A]_{0}-[P]_{t}\right) = \ln{[A]_{0}} - k^{\prime} t \label{13.13}\]

que simplificamos escribiendo en forma exponencial.

\[[A]_0 - [P]_t = [A]_0 e^{-k^{\prime}t} \label{13.14}\]

Finalmente, resolver la Ecuación\ ref {13.14} para [A] ₀ da la siguiente ecuación.

\[[A]_{0}=\frac{[P]_{t}}{1-e^{-k^{\prime}t}} \label{13.15}\]

Ejemplo 13.2.2

La concentración de tiocianato, SCN ^—, se determina a partir de la cinética de pseudo-primer orden de su reacción con exceso de Fe ^{3 +} para formar un complejo de color rojizo de Fe (SCN) ²⁺. El progreso de la reacción se monitorea midiendo la absorbancia de Fe (SCN) ²⁺ a una longitud de onda de 480 nm. Cuando se usa una solución estándar de SCN 0.100 M ^—, la concentración de Fe (SCN) ²⁺ después de 10 s es 0.0516 M. La concentración de Fe (SCN) ²⁺ en una muestra que contiene una cantidad desconocida de SCN ^— es 0.0420 M después de 10 s. Cuál es la concentración inicial de SCN ^— en la muestra?

Solución

Primero, debemos determinar un valor para la constante de velocidad de pseudo-primer orden,\(k^{\prime}\). Usando la ecuación\ ref {13.13}, encontramos que su valor es

\[k^{\prime} = \frac{\ln{[A]_{0}} - \ln \left([A]_{0} - [P]_{1}\right)}{t}= \frac {\ln(0.100) - \ln(0.100 - 0.0516)} {10.0 \text{ s}} = 0.0726 \text{ s}^{-1} \nonumber\]

A continuación, utilizamos la Ecuación\ ref {13.15} para determinar la concentración inicial de SCN ^— en la muestra.

\[[A]_{0}=\frac{[P]_{t}}{1-e^{-k^{\prime} t}}=\frac{0.0420 \mathrm{M}}{1-e^{-\left(0.0726 \text{ s}^{-1}\right)(10.0 \text{ s})}}=0.0868 \mathrm{M} \nonumber\]

Ejercicio 13.2.2

^{En una determinación separada para SCN, una serie de estándares externos da las siguientes concentraciones de Fe (SCN) 2+ después de una reacción de 10.0 s con exceso de Fe 3 + en condiciones de pseudo-primer orden.}

[SCN ^-] (M)	[Fe (SCN) ^2+] t = 10.0 s (M)
\(5.00 \times 10^{-3}\)	\(1.79 \times 10^{-3}\)
\(1.50 \times 10^{-2}\)	\(8.24 \times 10^{-3}\)
\(2.50 \times 10^{-2}\)	\(1.28 \times 10^{-2}\)
\(3.50 \times 10^{-2}\)	\(1.85 \times 10^{-2}\)
\(4.50 \times 10^{-2}\)	\(2.21 \times 10^{-2}\)
\(5.50 \times 10^{-2}\)	\(2.81 \times 10^{-2}\)
\(6.50 \times 10^{-2}\)	\(3.27 \times 10^{-2}\)
\(7.50\times 10^{-2}\)	\(3.91 \times 10^{-2}\)
\(8.50 \times 10^{-2}\)	\(4.23 \times 10^{-2}\)
\(9.50 \times 10^{-2}\)	\(4.89 \times 10^{-2}\)

El análisis de una muestra en las mismas condiciones da una concentración de Fe (SCN) ²⁺ de\(3.52 \times 10^{-2}\) M después de 10 s. ¿Cuál es la concentración inicial de SCN ^— en la muestra?

Contestar

La curva de calibración y la ecuación de calibración para los estándares externos se muestran a continuación. Sustituyendo\(3.52 \times 10^{-2}\) M por [Fe (SCN) ²⁺] _{t = 10 s} da [SCN ^—] ₀ como\(6.87 \times 10^{-2}\) M.

Un método integral de tiempo fijo de un punto tiene la ventaja de la simplicidad porque solo necesitamos una sola medición para determinar la concentración inicial del analito. Al igual que con cualquier método que se base en una sola determinación, un método integral de tiempo fijo de un punto no puede compensar un error determinado constante. En un método integral de tiempo fijo de dos puntos, corrigimos errores constantes determinados realizando mediciones en dos puntos en el tiempo y usamos la diferencia entre las mediciones para determinar la concentración inicial del analito. Debido a que afecta ambas mediciones por igual, la diferencia entre las mediciones es independiente de un error de terminación constante. Para una reacción de pseudo-primer orden en la que medimos la concentración del analito en los tiempos t ₁ y t ₂, podemos escribir las siguientes dos ecuaciones.

\[[A]_{t_{1}}=[A]_{0} e^{-k^{\prime} t_1} \label{13.16}\]

\[[A]_{t_{2}}=[A]_{0} e^{-k^{\prime} t_2} \label{13.17}\]

Restar la ecuación\ ref {13.17} de la ecuación\ ref {13.16} y resolver para [A] ₀ nos deja con

\[[A]_{0}=\frac{[A]_{t_1}-[A]_{t_2}}{e^{-k^{\prime} t_{1}}-e^{-k^{\prime} t_{2}}} \label{13.18}\]

Para determinar la constante de velocidad\(k^{\prime}\),, medimos\([A]_{t_1}\) y\([A]_{t_2}\) para una solución estándar de analito. Habiendo obtenido un valor para\(k^{\prime}\), podemos determinar [A] ₀ midiendo la concentración del analito en t ₁ y t ₂. También podemos determinar la concentración inicial del analito usando una curva de calibración que consiste en una gráfica de (\([A]_{t_1}\)—\([A]_{t_2}\)) versus [A] ₀.

Un método integral de tiempo fijo es particularmente útil cuando la señal es una función lineal de concentración porque podemos reemplazar la concentración del reactivo con la señal correspondiente. Por ejemplo, si seguimos una reacción espectrofotométricamente en condiciones donde la concentración del analito obedece a la ley de Beer

\[(A b s)_{t}=\varepsilon b[A]_{t} \nonumber\]

entonces podemos reescribir la Ecuación\ ref {13.8} y la Ecuación\ ref {13.18} como

\[(A b s)_{t}=[A]_{0} e^{-k^{\prime}} \varepsilon b=c[A]_{0} \nonumber\]

\[[A]_t = \frac {(Abs)_{t_1} - (Abs)_{t_2}} {e^{-k^{\prime}t_1} - e^{-k^{\prime}t_2}} \times (\epsilon b)^{-1} = c^{\prime}[(Abs)_{t_1} - (Abs)_{t_2}] \nonumber\]

donde (Abs) _t es la absorbancia en el tiempo t, y c y\(c^{\prime}\) son constantes.

Métodos Integrales de Tiempo Variable de Computación Directa

En un método integral de tiempo variable medimos el tiempo total,\(\Delta_t\), necesario para efectuar un cambio específico en la concentración para una especie en la reacción química. Una aplicación importante es el análisis cuantitativo de catalizadores, que aprovecha la capacidad del catalizador para aumentar la velocidad de reacción. A medida que la concentración de catalizador aumentó,\(\Delta_t\) disminuye. Para muchos sistemas catalíticos, la relación entre\(\Delta_t\) y la concentración del catalizador es

\[\frac {1} {\Delta t} = F_{cat}[A]_0 + F_{uncat} \label{13.19}\]

donde [A] ₀ es la concentración del catalizador, y F _cat y F _uncat son constantes que dan cuenta de la velocidad de las reacciones catalizadas y no catalizadas [Mark, H. B.; Rechnitz, G. A. Cinética en Química Analítica, Interciencia: Nueva York, 1968].

Ejemplo 13.2.3

Sandell y Kolthoff desarrollaron un método cuantitativo para yoduro basado en su capacidad para catalizar la siguiente reacción redox [Sandell, E. B.; Kolthoff, I. M. J. Am. Chem. Soc. 1934, 56, 1426].

\[\mathrm{As}^{3+}(a q)+2 \mathrm{Ce}^{4+}(a q) \longrightarrow \mathrm{As}^{\mathrm{5+}}(a q)+2 \mathrm{Ce}^{3+}(a q) \nonumber\]

Se preparó una curva de calibración de patrones externos añadiendo 1 mL de un patrón KI a una mezcla de 2 mL de 0.05 M As ^{3 +}, 1 mL de 0.1 M Ce ^{4 +}, y 1 mL de 3 M H ₂ SO ₄, y midiendo el tiempo para el color amarillo de Ce ^{4 +} a desaparecer. En la siguiente tabla se resumen los resultados para un análisis.

[I ^-] (µg/mL)	\(\Delta_t\)(min)
5.0	\ (\ Delta_t\) (min) ">0.9
2.5	\ (\ Delta_t\) (min) ">1.8
1.0	\ (\ Delta_t\) (min) ">4.5

¿Cuál es la concentración de I ^— en una muestra si\(\Delta_t\) es 3.2 min?

Solución

La Figura 13.2.2 muestra la curva de calibración y la ecuación de calibración para los estándares externos basados en la Ecuación\ ref {13.19}. Sustituyendo 3.2 min por\(\Delta_t\) da la concentración de I ^— en la muestra como 1.4 μg/mL.

Figura 13.2.2 . Curva de calibración y ecuación de calibración para el Ejemplo 13.2.3.

Métodos de tasa de cálculo directo

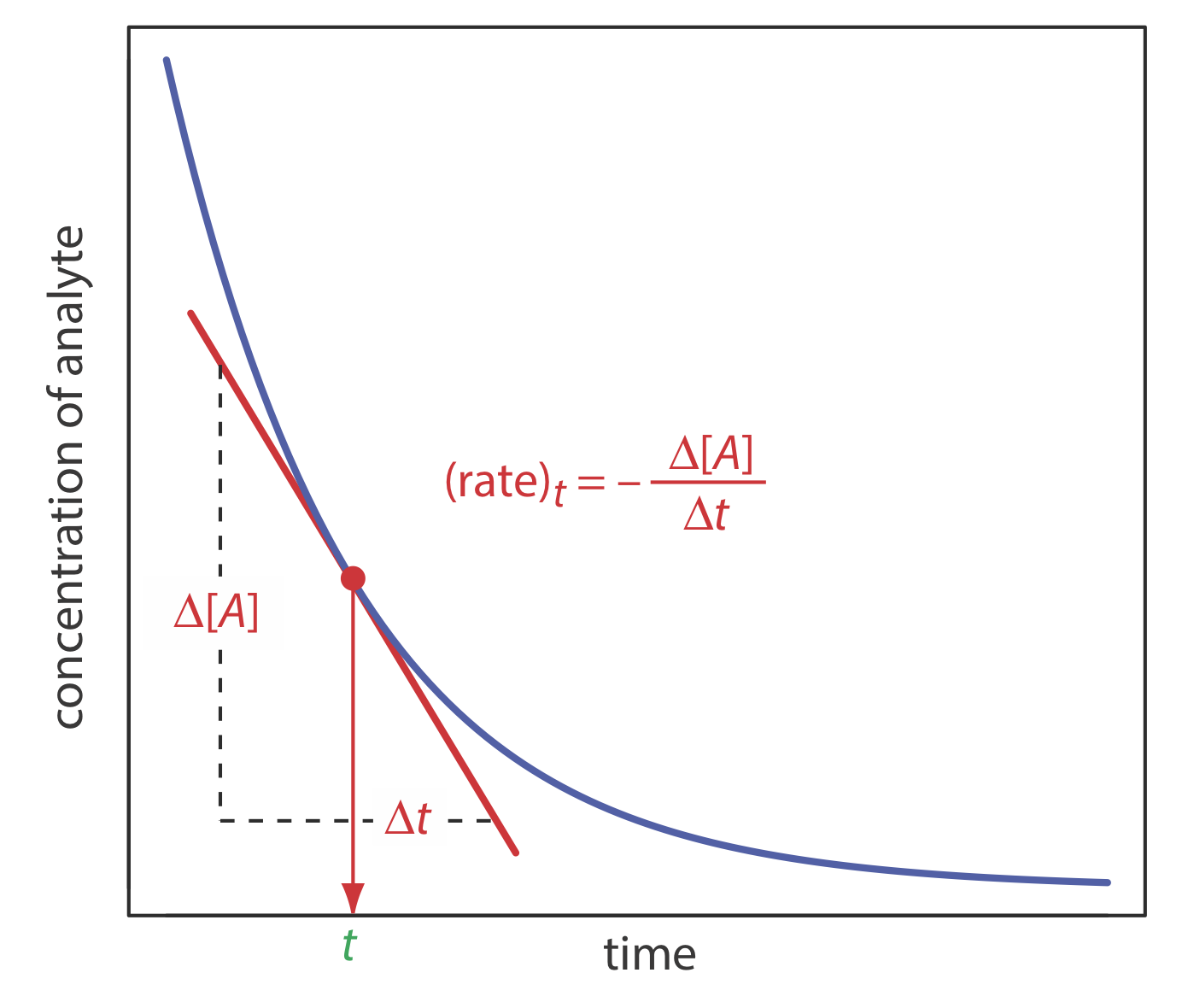
En un método de tasa utilizamos la forma diferencial de la ley de velocidad, la ecuación\ ref {13.1} es un ejemplo de una ley de tasa diferencial, para determinar la concentración del analito. Como se muestra en la Figura 13.2.3 , la velocidad de una reacción en el tiempo t, (tasa) _t, es la pendiente de una línea tangente a una curva que muestra el cambio en la concentración en función del tiempo. Para una reacción que es de primer orden en el analito, la velocidad en el tiempo t es

\[(r a t e)_{t}=k[A]_{t} \nonumber\]

Sustituir en la Ecuación\ ref {13.3} nos deja con la siguiente ecuación que relaciona la tasa en el tiempo t con la concentración inicial del analito.

\[(\text {rate})_{t}=k[A]_{0} e^{-k t} \nonumber\]

Si medimos la tasa en un tiempo fijo, entonces tanto k como e ^{— kt} son constantes y podemos usar una curva de calibración de (tasa) _t versus [A] ₀ para el análisis cuantitativo del analito.

Figura 13.2.3 . Determinación de la velocidad instantánea de una reacción en el tiempo t desde la pendiente de una línea tangente a una curva que muestra el cambio en la concentración del analito en función del tiempo.

Hay varias ventajas al usar la velocidad inicial de la reacción (t = 0). Primero, debido a que la velocidad de la reacción disminuye con el tiempo, la velocidad inicial proporciona la mayor sensibilidad. Segundo, debido a que la tasa inicial se mide bajo condiciones de orden casi pseudo-cero, en las que el cambio en la concentración con el tiempo efectivamente es lineal, es más fácil determinar la pendiente. Finalmente, a medida que avanza la reacción de interés pueden desarrollarse reacciones competitivas, lo que complica la cinética: usar la tasa inicial elimina estas complicaciones. Una desventaja del método de velocidad inicial es que puede haber tiempo insuficiente para mezclar completamente los reactivos. Este problema se evita mediante el uso de una tasa intermedia medida en un momento posterior (t > 0).

Como regla general (ver Mottola, H. A. “Determinaciones cinéticas de reactivos que utilizan reacciones no catalizadas”, Anal. Chim. Acta 1993, 280, 279—287), el tiempo para medir la velocidad inicial de una reacción debe resultar en el consumo de no más del 2% de los reactivos. Cuanto menor sea este porcentaje, más lineal será el cambio en la concentración en función del tiempo.

Ejemplo 13.2.4

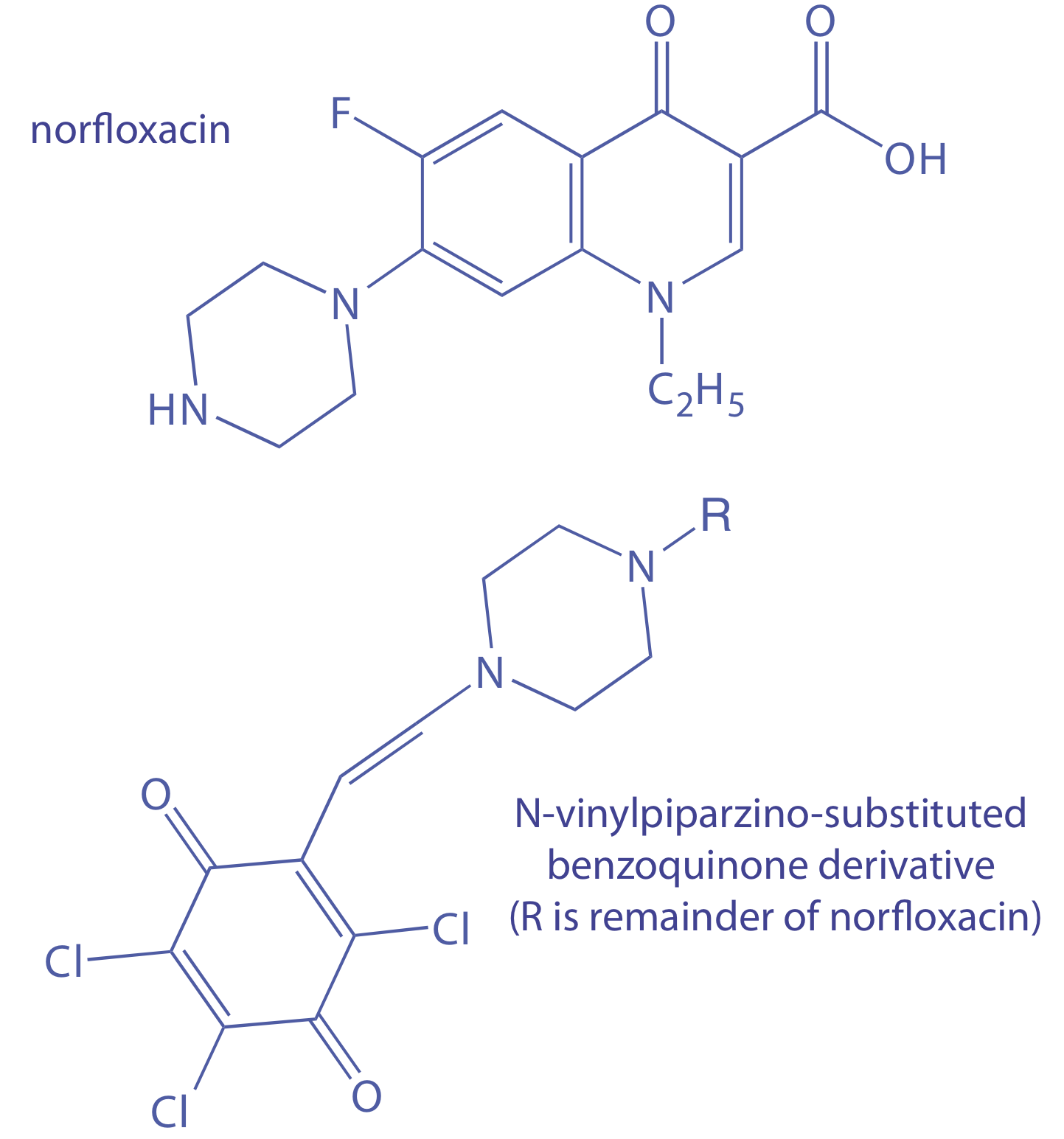
La concentración de norfloxacino, un agente antibacteriano comúnmente prescrito, se determina mediante el método de tasa inicial. La norfloxacina se convierte en un derivado de N-vinilpiperazina y se hace reaccionar con 2,3,5,6-tetra-cloro-1,4-benzoquinona para formar un derivado de ben-zoquinona N-vinilpiperazino-sustituido que absorbe fuertemente a 625 nm [Darwish, I. A.; Sultan, M. A.; Al-Arfaj, H. A. Talanta 2009, 78, 1383—1388]. La tasa inicial de reacción, medida por el cambio en la absorbancia en función del tiempo (AU/min), es de pseudo-primer orden en norfloxacino. Se obtuvieron los siguientes datos para una serie de estándares externos de norfloxacino.

[norfloxacina] (µg/mL)	tasa inicial (AU/min)
63	0.0139
125	0.0355
188	0.0491
251	0.0656
313	0.0859

Para analizar una muestra de gotas oculares recetadas, se extrae una porción de 10.00 ml con diclorometano. El extracto se seca y la norfloxacina se reconstituye en metanol y se diluye a 10 mL en un matraz aforado. Una porción de 5.00-mL de esta solución se diluye a volumen en un matraz aforado de 100 mL. El análisis de esta muestra da una tasa inicial de 0.0394 AU/min.

¿Cuál es la concentración de norfloxacino en las gotas oculares en mg/mL?

Solución

La Figura 13.2.4 muestra la curva de calibración y la ecuación de calibración para los estándares externos. Sustituir 0.0394 AU/min por la tasa inicial y resolver la concentración de norfloxacino da un resultado de 152 μg/mL. Esta es la concentración en una muestra diluida del extracto. La concentración en el extracto antes de la dilución es

\[\frac{152 \: \mu \text{g}}{\mathrm{mL}} \times \frac{100.0 \: \mathrm{mL}}{5.00 \: \mathrm{mL}} \times \frac{1 \:\mathrm{mg}}{1000 \: \mu \mathrm{g}}=3.04 \: \mathrm{mg} / \mathrm{mL} \nonumber\]

Debido a que el extracto seco se reconstituyó utilizando un volumen idéntico al de la muestra original, la concentración de norfloxacina en las gotas oculares es de 3.04 mg/mL.

Figura 13.2.4 . Curva de calibración y ecuación de calibración para el Ejemplo 13.2.4 .

Métodos de ajuste de curvas

En un método de cálculo directo determinamos la concentración del analito resolviendo la ecuación de velocidad apropiada en uno o dos tiempos discretos. La relación entre la concentración del analito y la respuesta medida es una función de la constante de velocidad, que determinamos en un experimento separado usando un único estándar externo (ver Ejemplo 13.2.1 o Ejemplo 13.2.2), o una curva de calibración (ver Ejemplo 13.2.3 o Ejemplo 13.2.4).

En un método de ajuste de curvas monitoreamos continuamente la concentración de un reactivo o un producto en función del tiempo y utilizamos un análisis de regresión para ajustar los datos a una ley de tasa diferencial apropiada o ley de tasa integrada. Por ejemplo, si estamos monitoreando la concentración de un producto para una reacción que es pseudo-de primer orden en el analito, entonces podemos ajustar los datos a la siguiente forma reordenada de la Ecuación\ ref {13.15}

\[[P]_{t}=[A]_{0}\left(1-e^{-k^{\prime} t}\right) \nonumber\]

usando [A] ₀ y\(k^{\prime}\) como parámetros ajustables. Debido a que utilizamos datos de más de uno o dos tiempos discretos, un método de ajuste de curvas es capaz de producir resultados más confiables.

Ejemplo 13.2.5

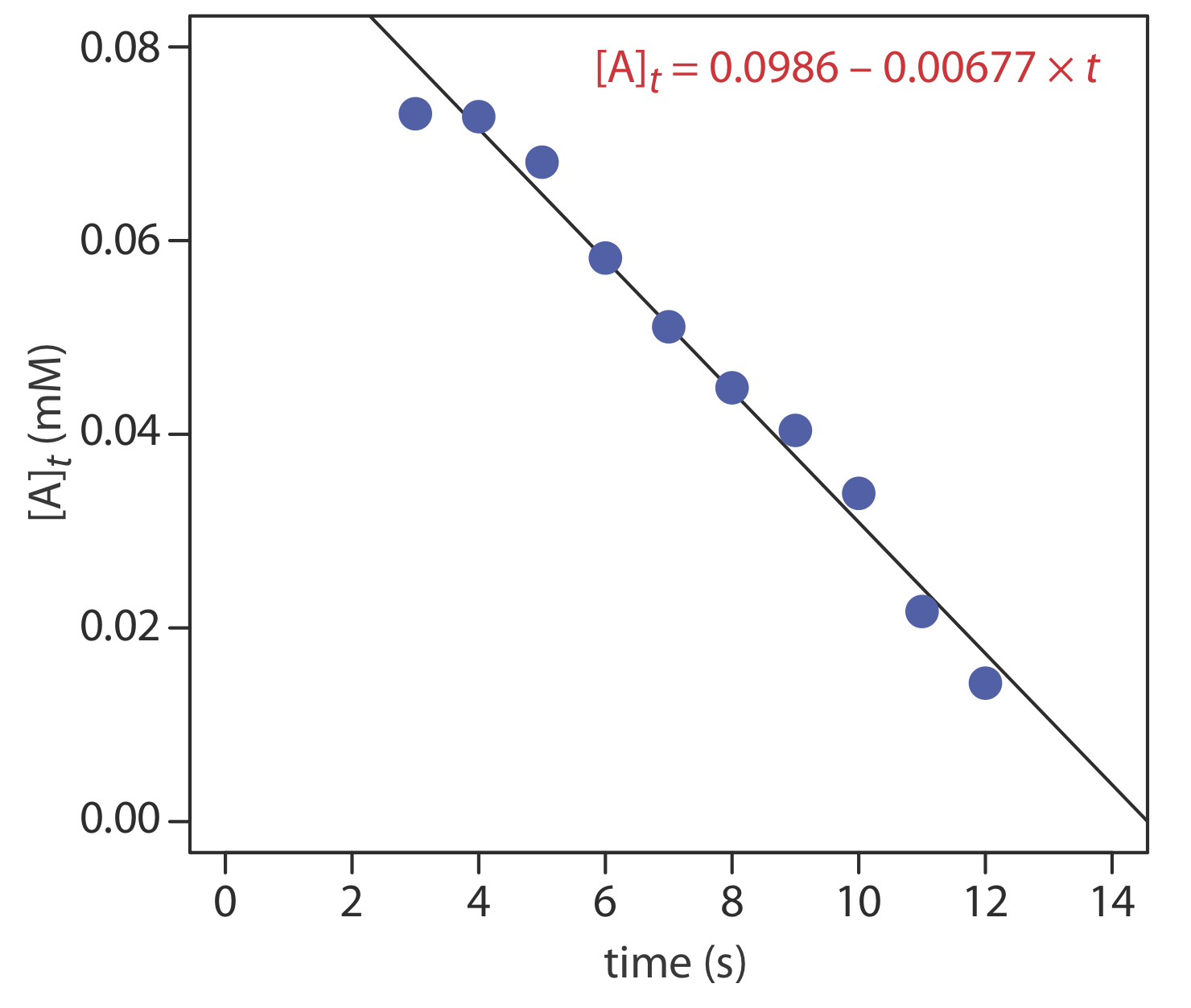
Los datos mostrados en la siguiente tabla fueron recolectados para una reacción que se sabe que es de orden pseudo-cero en analito. ¿Cuál es la concentración inicial de analito en la muestra y la constante de velocidad para la reacción?

tiempo (s)	[A] t (mM)	tiempo (s)	[A] t (mM)
3	0.0731	8	0.0448
4	0.0728	9	0.0404
5	0.0681	10	0.0339
6	0.0582	11	0.0217
7	0.0511	12	0.0143

Solución

De la Ecuación\ ref {13.10} sabemos que para una reacción de pseudo-orden cero una gráfica de [A] _t versus tiempo es lineal con una pendiente de\(-k^{\prime \prime}\) y una intercepción y de [A] ₀. La Figura 13.2.5 muestra una gráfica de los datos cinéticos y el resultado de un análisis de regresión lineal. La concentración inicial de analito es 0.0986 mM y la constante de velocidad es 0.00677 M ^—1 s ^—1.

Figura 13.2.5 . Resultado del ajuste de la Ecuación\ ref {13.10} a los datos del Ejemplo 13.2.5 .

La mejor manera de apreciar los detalles teóricos y prácticos discutidos en esta sección es examinar cuidadosamente un método analítico típico. Si bien cada método es único, la siguiente descripción de la determinación de creatinina en orina proporciona un ejemplo instructivo de un procedimiento típico. La descripción aquí se basa en Diamandis, E. P.; Koupparis, M. A.; Hadjiioannou, T. P. “Estudios cinéticos con electrodos selectivos de iones: determinación de creatinina en orina con un electrodo selectivo de iones picrato”, J. Chem. Educ. 1983, 60, 74—76.

Método Representativo 13.2.1: Determinación de Creatinina en Orina

Descripción del método

La creatina es un ácido orgánico en el tejido muscular que suministra energía para las contracciones musculares. Uno de sus productos metabólicos es la creatinina, que se excreta en la orina. Debido a que la concentración de creatinina en orina y suero es una indicación importante de la función renal, un método rápido para su análisis es clínicamente importante. En este método se utiliza la velocidad de reacción entre creatinina y picrato en un medio alcalino para determinar la concentración de creatinina en orina. Bajo las condiciones del análisis la reacción es de primer orden en picrato, creatinina e hidróxido.

\[\text { rate }=k[\text { picrate }][\text { creatinine }]\left[\mathrm{OH}^{-}\right] \nonumber\]

La reacción se controla usando un electrodo selectivo de iones picrato.

Procedimiento

Preparar un conjunto de estándares externos que contengan 0.5—3.0 g/L de creatinina usando una solución madre de 10.00 g/L de creatinina en 5 mM H ₂ SO ₄, diluyendo cada patrón al volumen usando 5 mM H ₂ SO ₄. Preparar una solución de picrato de sodio\(1.00 \times 10^{-2}\) M. Pipeta 25.00 mL de NaOH 0.20 M, ajustada a una fuerza iónica de 1.00 M usando Na ₂ SO ₄, en una celda de reacción termostatizada a 25 ^o C. Añadir 0.500 mL de la solución de picrato\(1.00 \times 10^{-2}\) M a la celda de reacción. Suspender un selectivo de iones picrato en la solución y monitorear el potencial hasta que se estabilice. Cuando el potencial es estable, agregar 2.00 mL de un estándar externo de creatinina y registrar el potencial en función del tiempo. Repita este procedimiento utilizando los estándares externos restantes. Construir una curva de calibración\(\Delta E / \Delta t\) frente a la concentración inicial de creatinina. Utilizar el mismo procedimiento para analizar muestras, utilizando 2.00 mL de orina en lugar del estándar externo. Determinar la concentración de creatinina en la muestra usando la curva de calibración.

Preguntas

1. El análisis se realiza bajo condiciones que son de pseudo-primer orden en picrate. Demostrar que bajo estas condiciones el cambio de potencial en función del tiempo es lineal.

El potencial, E, del electrodo selectivo de iones picrato viene dado por la ecuación de Nernst

\[E=K-\frac{R T}{F} \ln{[\text { picrate }]} \nonumber\]

donde K es una constante que da cuenta de los electrodos de referencia, los potenciales de unión y el potencial de asimetría del electrodo selectivo de iones, R es la constante de gas, T es la temperatura y F es la constante de Faraday. Sabemos por la Ecuación\ ref {13.7} que para una reacción de pseudo-primer orden, la concentración de picrate en el tiempo t es

\[\ln {[\text{picrate}]_t}=\ln{[\text {picrate}]}_{0}-k^{\prime} t \nonumber\]

donde\(k^{\prime}\) es la constante de velocidad de pseudo-primer orden. Sustituir esta ley de velocidad integrada en la ecuación de Nernst del electrodo selectivo de iones nos deja con el siguiente resultado.

\[E_{t} = K - \frac{R T} {F} \left( \ln{[\text {picrate}]}_{0} - k^{\prime} t\right) \nonumber\]

\[E_{t} = K - \frac{R T} {F} \ln{[\text {picrate}]}_{0} + \frac{R T} {F} k^{\prime}t \nonumber\]

Debido a que K y (RT/F) ln [picrate] ₀ son constantes, una gráfica de E _t versus t es una línea recta con una pendiente de\(\frac{R T} {F} k^{\prime}\).

2. Bajo las condiciones del análisis, la velocidad de la reacción es pseudo-primer orden en picrate y pseudo-orden cero en creatinina y OH ^—. Explicar por qué es posible preparar una curva de calibración de\(\Delta E / \Delta t\) versus la concentración de creatinina.

La pendiente de una parcela de E _t versus t es\(\Delta E / \Delta t = RTk^{\prime}/F\) = RTk ′/ F (ver la pregunta anterior). Debido a que la reacción se lleva a cabo bajo condiciones donde es de orden pseudo-cero en creatinina y OH ^—, la ley de tasa es

\[\text{rate} = k[\text{picrate}][\text{creatinine}]_0[\text{OH}^-]_0 = k^{\prime}[\text{picrate}] \nonumber\]

La constante de velocidad de pseudo-primer orden,\(k^{\prime}\), es

\[k^{\prime}=k[\text { creatinine }]_{0}\left[\mathrm{OH}^{-}\right]_{0}=c[\text {creatinine}]_{0} \nonumber\]

donde c es una constante equivalente a k [OH ^-] ₀. La pendiente de una gráfica de E _{t versus t}, por lo tanto, es función lineal de la concentración inicial de creatinina

\[\frac{\Delta E}{\Delta t}=\frac{R T k^{\prime}}{F}=\frac{R T c}{F}[\text {creatinine}]_{0} \nonumber\]

y una gráfica de\(\Delta E / \Delta t\) versus la concentración de creatinina puede servir como curva de calibración.

3. ¿Por qué es necesario termostato la celda de reacción?

La velocidad de una reacción es dependiente de la temperatura. La celda de reacción se termostatiza para mantener una temperatura constante para evitar un error determinado por un cambio sistemático de temperatura, y para minimizar los errores indeterminados de fluctuaciones aleatorias de temperatura.

4. ¿Por qué es necesario preparar la solución de NaOH para que tenga una fuerza iónica de 1.00 M?

El potencial del electrodo selectivo de iones picrato responde realmente a la actividad del anión picrato en solución. Ajustando la solución de NaOH a una alta fuerza iónica mantenemos una fuerza iónica constante en todos los estándares y muestras. Debido a que la relación entre actividad y concentración es una función de la fuerza iónica, el uso de una fuerza iónica constante nos permite escribir la ecuación de Nernst en términos de concentración de picrato en lugar de su actividad.

Realización de mediciones cinéticas

Al utilizar el Método Representativo 13.2.1 para determinar la concentración de creatinina en orina, seguimos la cinética de las reacciones usando un electrodo selectivo de iones. En principio, podemos utilizar cualquiera de las técnicas analíticas de los Capítulos 8-12 para seguir la cinética de una reacción siempre que la reacción no proceda en una medida apreciable durante el tiempo que lleva realizar una medición. Como cabría esperar, este requisito impone una seria limitación a los métodos cinéticos de análisis. Si la cinética de la reacción es lenta en relación con el tiempo de análisis, entonces podemos hacer una medición sin que el analito sufra un cambio significativo en la concentración. Si la velocidad de la reacción es demasiado rápida, lo que suele ser el caso, entonces introducimos un error significativo si nuestro tiempo de análisis es demasiado largo.

Una solución a este problema es detener o apagar la reacción ajustando las condiciones experimentales. Por ejemplo, muchas reacciones muestran una fuerte dependencia del pH y se extinguen añadiendo un ácido fuerte o una base fuerte. La Figura 13.2.6 muestra un ejemplo típico para el análisis enzimático de p-nitrofenilfosfato, que utiliza la enzima fosfatasa ácida de germen de trigo para hidrolizar el analito a p-nitrofenol. La reacción tiene una velocidad máxima a un pH de 5. Al aumentar el pH mediante la adición de NaOH se apaga la reacción y se convierte el p-nitrofenol incoloro en el p-nitrofenolato de color amarillo, el cual absorbe a 405 nm.

Figura 13.2.6 . Tasa inicial para la hidrólisis enzimática de p-nitrofenilfosfato usando fosfatasa ácida de germen de trigo. Al aumentar el pH se apaga la reacción y se cubre el p-nitrofenol incoloro al p-nitrofenolato de color amarillo, el cual absorbe a 405 nm.

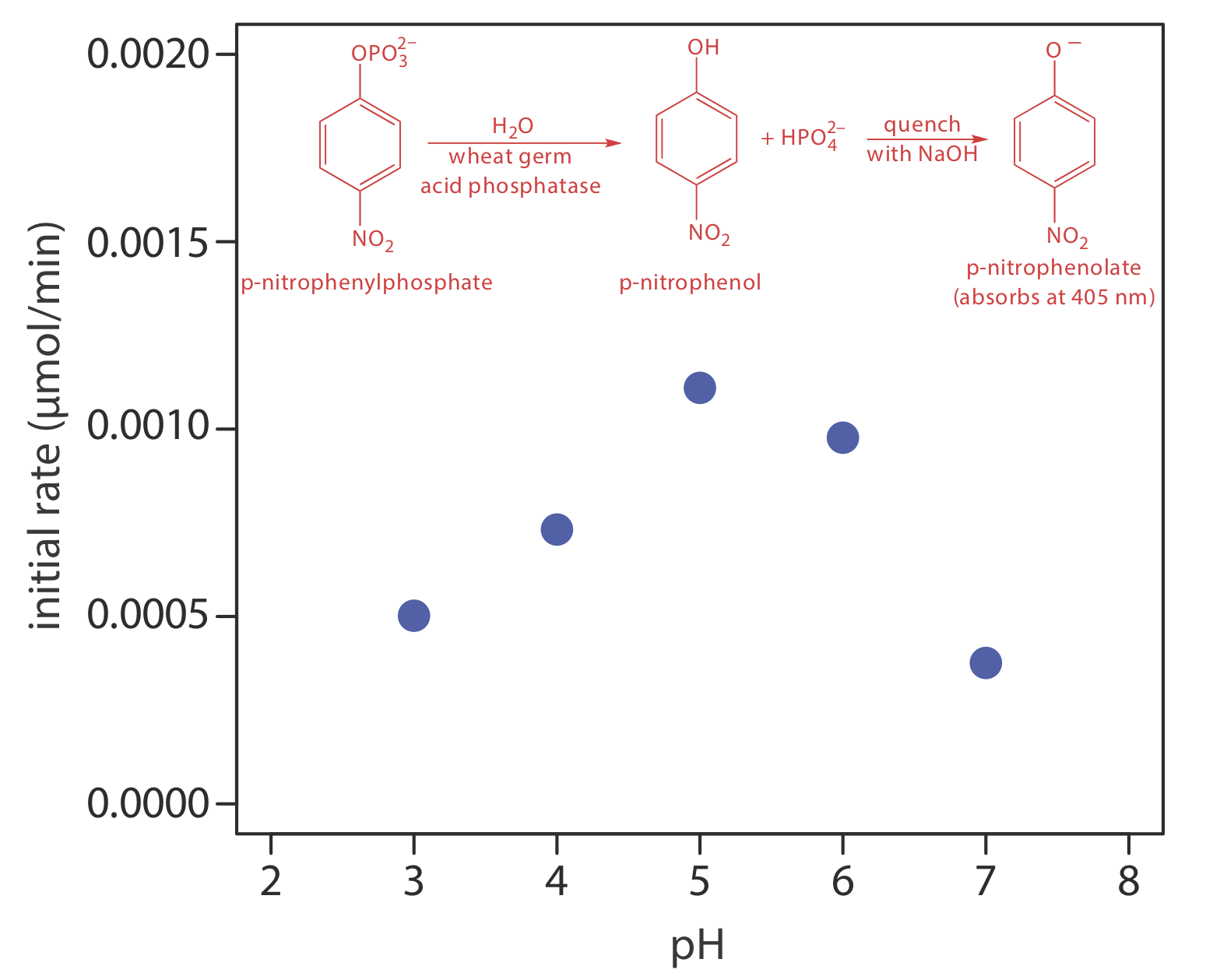
Un problema adicional cuando la cinética de la reacción es rápida es asegurar que mezclamos rápida y reproduciblemente la muestra y los reactivos. Para una reacción rápida, necesitamos hacer nuestras mediciones dentro de unos segundos, o incluso unos pocos milisegundos, de combinar la muestra y los reactivos. Esto nos presenta un problema y una ventaja. El problema es que la mezcla rápida y reproducible de la muestra y el reactivo requiere un instrumento dedicado, lo que agrega un gasto adicional al análisis. La ventaja es que un análisis rápido y automatizado permite un alto rendimiento de muestras. Los instrumentos para el análisis cinético automatizado de fosfato usando reacción\ ref {13.11}, por ejemplo, tienen velocidades de muestreo de aproximadamente 3000 determinaciones por hora.

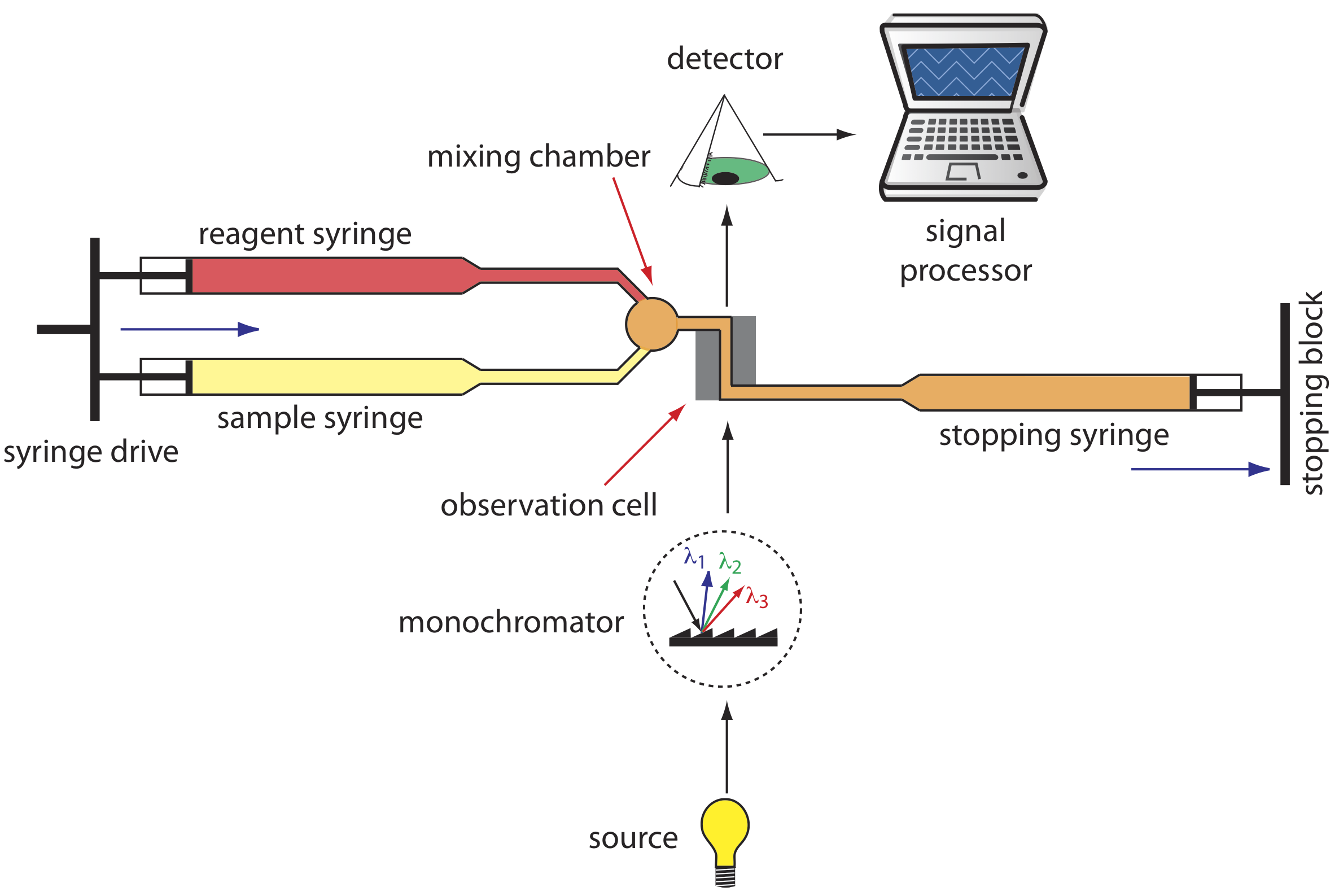
Se han desarrollado diversos instrumentos para automatizar el análisis cinético de reacciones rápidas. Un ejemplo, que se muestra en la Figura 13.2.7 , es el analizador de flujo detenido. La muestra y los reactivos se cargan en jeringas separadas y los volúmenes medidos con precisión se dispensan en una cámara de mezcla por la acción de un accionamiento de jeringa. La acción continuada del accionamiento de la jeringa empuja la mezcla a través de una celda de observación y dentro de una jeringa de detención. La contrapresión generada cuando la jeringa de detención golpea el bloque de detención completa la mezcla, después de lo cual se monitorea espectrofotométricamente el progreso de la reacción. Con un analizador de flujo detenido es posible completar la mezcla de muestra y reactivo, e iniciar las mediciones cinéticas en aproximadamente 0.5 ms. Al conectar un automuestreador a la jeringa de muestra es posible analizar hasta varios cientos de muestras por hora.

Figura 13.2.7 . Diagrama esquemático de un analizador de flujo parado. Las flechas azules muestran la dirección en la que se mueven las jeringas.

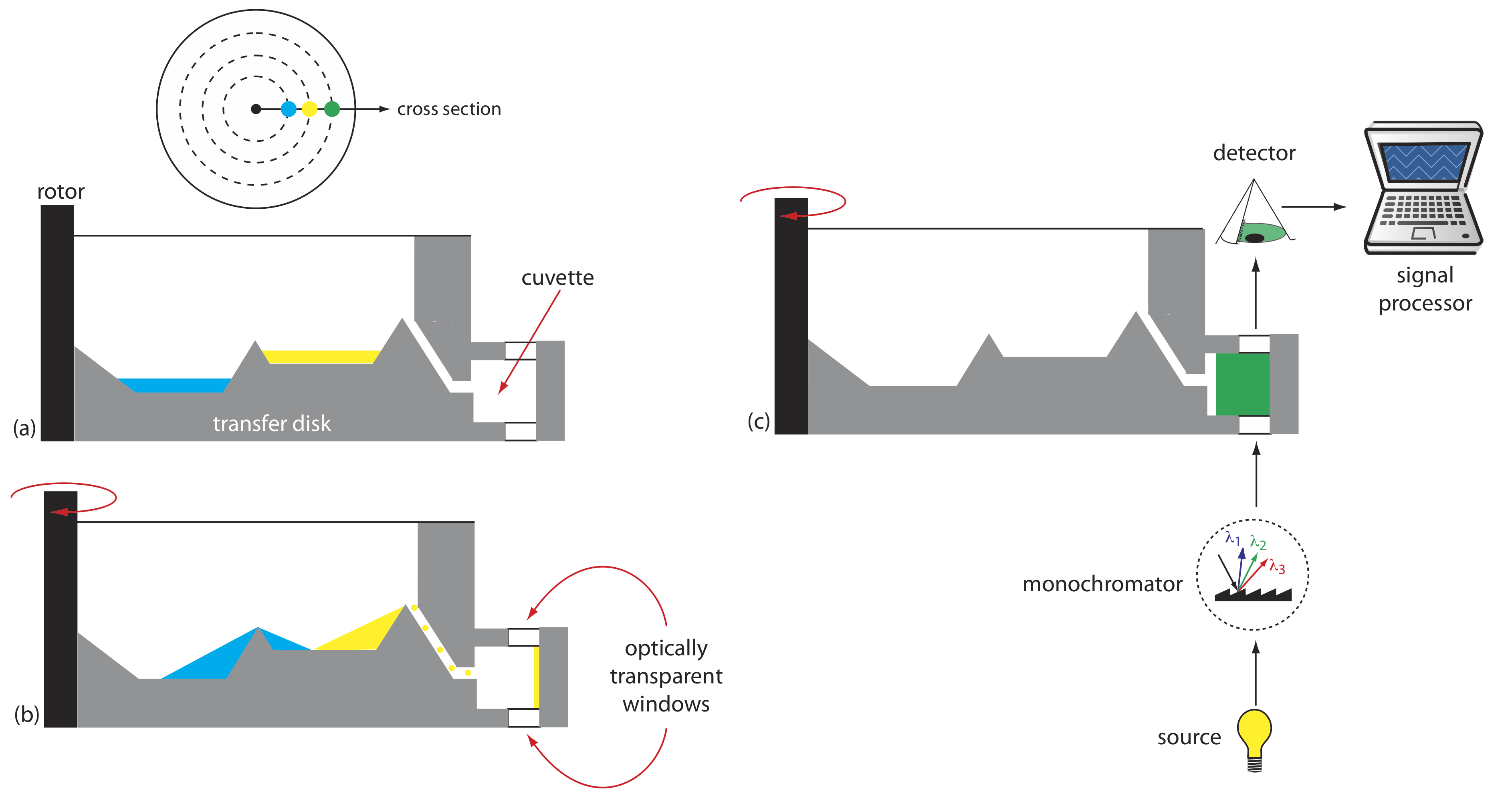
Otro instrumento para mediciones cinéticas es el analizador centrífugo, una sección transversal parcial del cual se muestra en la Figura 13.2.8 . La muestra y los reactivos se colocan en pocillos separados, los cuales están orientados radialmente alrededor de un disco de transferencia circular. A medida que la centrífuga gira, la fuerza centrífuga tira de la muestra y los reactivos hacia la cubeta donde se produce la mezcla. Una única fuente óptica y detector, ubicados debajo y por encima del borde exterior del disco de transferencia, mide la absorbancia cada vez que la cubeta pasa a través del haz óptico. Al usar un disco de transferencia con 30 cubetas y rotar a 600 rpm, podemos recolectar 10 puntos de datos por segundo para cada muestra.

Figura 13.2.8 . Secciones transversales a través de un analizador centrífugo mostrando (a) los pocillos que contienen la muestra y los reactivos, (b) la mezcla de la muestra y los reactivos, y (c) la configuración del detector espectrofotométrico.

La capacidad de recopilar muchos datos y recopilarlos rápidamente requiere hardware y software adecuados. No es sorprendente que los analizadores cinéticos automatizados se desarrollaran en paralelo con los avances en circuitos analógicos y digitales, el hardware y el software de computadora para suavizar, integrar y diferenciar la señal analítica. Para una discusión temprana de la importancia del hardware y el software, véase Malmstadt, H. V.; Delaney, C. J.; Cordos, E. A. “Instrumentos para Determinaciones de Tasa”, Anal. Chem. 1972, 44 (12), 79A—89A.

Aplicaciones Cuantitativas

Los métodos de análisis cinéticos químicos continúan encontrando utilidad para el análisis de una variedad de analitos, especialmente en laboratorios clínicos donde los métodos automatizados ayudan a manejar el gran volumen de muestras. En esta sección consideramos varias aplicaciones cuantitativas generales.

Reacciones catalizadas por enzimas

Las enzimas son catalizadores altamente específicos para reacciones bioquímicas, mostrando cada enzima una selectividad por un solo reactivo, o sustrato. Por ejemplo, la enzima acetilcolinesterasa cataliza la descomposición del neurotransmisor acetilcolina a colina y ácido acético. Muchas reacciones enzima-sustrato siguen un mecanismo simple que consiste en la formación inicial de un complejo enzima-sustrato, ES, que posteriormente se descompone para formar producto, liberando la enzima para reaccionar de nuevo.

\ [E + S\ underset {k_ {-1}} {\ stackrel {k_1} {\ rightleftharpoons}} ES\ underset {k_ {-2}} {\ stackrel {k_2} {\ rightleftharpoons}} E + P
\ label {13.20}\]

donde k ₁, k _—1, k ₂ y k _—2 son constantes de velocidad. Si hacemos la medición temprano en la reacción, la concentración de productos es insignificante y podemos ignorar el paso descrito por la constante de velocidad k _—2. Bajo estas condiciones, la velocidad de la reacción es

\[\text { rate }=\frac{d[P]}{d t}=k_{2}[E S] \label{13.21}\]

Para ser analíticamente útiles necesitamos escribir la Ecuación\ ref {13.21} en términos de las concentraciones de la enzima, E, y el sustrato, S. Para ello utilizamos la aproximación en estado estacionario, en la que asumimos que la concentración de ES permanece esencialmente constante. Después de un período inicial, durante el cual se forma primero el complejo enzima-sustrato, la velocidad a la que se forma ES

\[\frac{d[E S]}{d t}=k_{1}[E][S]=k_{1}\left([E]_{0}-[E S]\right)[S] \label{13.22}\]

es igual a la velocidad a la que desaparece

\[-\frac{d[E S]}{d t}=k_{-1}[E S]+k_{2}[E S] \label{13.23}\]

donde [E] ₀ es la concentración original de la enzima. Combinando la ecuación\ ref {13.22} y la ecuación\ ref {13.23} da

\[k_{1}\left([E]_{0}-[E S]\right)[S]=k_{-1}[E S]+k_{2}[E S] \nonumber\]

que resolvemos para la concentración del complejo enzima-sustrato

\[[E S]=\frac{[E]_{0}[S]}{\frac{k_{-1}+k_{2}}{k_{1}}+[S]}=\frac{[E]_{0}[S]}{K_{m}+[S]} \label{13.24}\]

donde K _m es la constante Michaelis. Sustituir la ecuación\ ref {13.24} en la ecuación\ ref {13.21} nos deja con nuestra ecuación de tasa final.

\[\frac{d[P]}{d t}=\frac{k_{2}[E]_{0}[S]}{K_{m}+[S]} \label{13.25}\]

Una gráfica de la Ecuación\ ref {13.25}, como se muestra en la Figura 13.2.9 , nos ayuda a definir condiciones donde podemos utilizar la velocidad de una reacción enzimática para el análisis cuantitativo de una enzima o un sustrato. Para altas concentraciones de sustrato, donde [S] >> K _m, Ecuación\ ref {13.25} simplifica a

\[\frac{d[P]}{d t}=\frac{k_{2}[E]_{0}[S]}{K_{m}+[S]} \approx \frac{k_{2}[E]_{0}[S]}{[S]}=k_{2}[E]_{0}=V_{\max } \label{13.26}\]

donde V _max es la velocidad máxima para la reacción catalizada. Bajo estas condiciones la reacción es de orden pseudo-cero en sustrato, y podemos usar V _max para calcular la concentración de la enzima, típicamente usando un método de tiempo variable. A concentraciones de sustrato más bajas, donde [S] << K _m, Ecuación\ ref {13.25} se convierte

\[\frac{d[P]}{d t}=\frac{k_{2}[E]_{0}[S]}{K_{m}+[S]} \approx \frac{k_{2}[E]_{0}[S]}{K_{m}}=\frac{V_{\max }[S]}{K_{m}} \label{13.27}\]

Debido a que la reacción es de primer orden en el sustrato, podemos usar la velocidad de reacción para determinar la concentración del sustrato usando un método de tiempo fijo.

Figura 13.2.9 . Gráfica de la Ecuación\ ref {13.25} mostrando límites para el análisis de sustratos y enzimas en un método de análisis cinético químico catalizado por enzimas. La curva en la región resaltada en rojo obedece a la Ecuación\ ref {13.27} y la curva en el área resaltada en verde sigue a la Ecuación\ ref {13.26}.

Se han aplicado métodos cinéticos químicos al análisis cuantitativo de varias enzimas y sustratos [Guilbault, G. G. Handbook of Enzymatic Methods of Analysis, Marcel Dekker: New York, 1976]. Un ejemplo, es la determinación de glucosa basada en su oxidación por la enzima glucosa oxidasa

\[\text{glucose}(aq) + \text{H}_2\text{O}(g) \xrightarrow{\text{glucose oxidase}} \text{gluconolactone}(aq) + \text{H}_2\text{O}_2(aq) \nonumber\]

bajo condiciones donde la Ecuación\ ref {13.20} es válida. La reacción se monitorea siguiendo la velocidad de cambio en la concentración de O ₂ disuelto usando una técnica voltamétrica apropiada.

Un método para medir la concentración de O ₂ disuelto es el sensor amperométrico Clark descrito en el Capítulo 11.

Reacciones no catalizadas por enzimas

El método de tiempo variable también se utiliza para determinar la concentración de catalizadores no enzimáticos. Un ejemplo utiliza la reducción de H ₂ O ₂ por tiosulfato, yoduro o hidroquinona, una reacción catalizada por trazas de iones metálicos seleccionados. Por ejemplo la reducción de H ₂ O ₂ por I ^—

\[2 \mathrm{I}^{-}(a q)+\mathrm{H}_{2} \mathrm{O}_{2}(a q)+2 \mathrm{H}_{3} \mathrm{O}^{+}(a q) \longrightarrow 4 \mathrm{H}_{2} \mathrm{O}(l)+\mathrm{I}_{2}(a q) \nonumber\]

es catalizado por Mo (VI), W (VI) y Zr (IV). Se realiza un análisis de tiempo variable añadiendo una pequeña cantidad fija de ácido ascórbico a cada solución. Como I ₂ se produce oxida rápidamente el ácido ascórbico y se reduce de nuevo a I ^—. Una vez consumido todo el ácido ascórbico, la presencia de exceso de I ₂ proporciona un punto final visual.

Reacciones no catalíticas

Los métodos cinéticos químicos no son tan comunes para el análisis cuantitativo de analitos en reacciones no catalíticas. Debido a que carecen del aumento de la velocidad de reacción que proporciona un catalizador, un método no catalítico generalmente no es útil para determinar pequeñas concentraciones de analito. Los métodos no catalíticos para analitos inorgánicos generalmente se basan en una reacción de complejación. Un ejemplo es la determinación de aluminio en suero midiendo la tasa inicial para la formación de su complejo con 2-hidroxi-1-naftaldehído p-metoxibenzoil-hidrazona [Ioannou. P. C.; Piperaki, E. A. Clin. Chem. 1986, 32, 1481—1483]. El mayor número de métodos no catalíticos, sin embargo, son para el análisis cuantitativo de analitos orgánicos. Por ejemplo, el insecticida metil paratión se ha determinado midiendo su tasa de hidrólisis en soluciones alcalinas [Cruces Blanco, C.; Garcia Sanchez, F. Int. J. Environ. Anal. Chem. 1990, 38, 513—523].

Aplicaciones de Caracterización

Los métodos cinéticos químicos también encuentran utilidad en la determinación de constantes de velocidad y en la elucidación de mecanismos de reacción. Dos ejemplos del análisis cinético de enzimas ilustran estas aplicaciones.

Determinación de V _max y K _m para reacciones catalizadas por enzimas

Los valores de V _max y K _m para una reacción enzimática son de interés significativo en el estudio de la química celular. Para una enzima que sigue el mecanismo de reacción\ ref {13.20}, V _max es equivalente a k 2\(\times\) [E] ₀, donde [E] ₀ es la concentración de la enzima y k ₂ es el recambio de la enzima número. El número de recambio de una enzima es el número máximo de moléculas de sustrato convertidas en producto por un solo sitio activo en la enzima, por unidad de tiempo. Un número de recambio, por lo tanto, proporciona una indicación directa de la eficiencia catalítica del sitio activo. La constante de Michaelis, K _m, es significativa porque proporciona una estimación de la concentración intracelular del sustrato [(a) Northup, D. B. J. Chem. Educ. 1998, 75, 1153—1157; b) Zubay, G. Bioquímica, Macmillan Publishing Co.: Nueva York, 2a Ed., p. 269].

El número de recambio de una enzima también se conoce como k _cat y es igual a V _max/[E] ₀. Para el mecanismo en reacción\ ref {13.20}, k _cat es equivalente a k ₂. Para mecanismos más complicados, k _cat es una función de constantes de velocidad adicionales.

Como se muestra en la Figura 13.2.9 , podemos encontrar valores para V _max y K _m midiendo la velocidad de reacción para concentraciones pequeñas y grandes del sustrato. Desafortunadamente, esto no siempre es práctico ya que la solubilidad limitada del sustrato puede impedirnos usar las grandes concentraciones de sustrato necesarias para determinar V _máx. Otro enfoque es reescribir la ecuación\ ref {13.25} tomando su recíproco

\ [\ frac {1} {d [P]/d t} =\ frac {1} {v} =\ frac {K_ {m}} {V_ {\ max}}\ veces\ frac {1} {[S]} +\ frac {1} {V_ {\ max}}\ etiqueta {13.28}\]

donde v es la velocidad de la reacción. Como se muestra en la Figura 13.2.10 , una gráfica de 1/ v versus 1/ [S], que se denomina gráfica doble recíproca o Lineweaver—Burk, es una línea recta con una pendiente de K _m/V _max, una intercepción y de 1/ V _max, y una intersección x de —1/ K _m.

Figura 13.2.10 . Lineweaver—Gráfica Burk de la Ecuación\ ref {13.25} usando la Ecuación\ ref {13.28}.

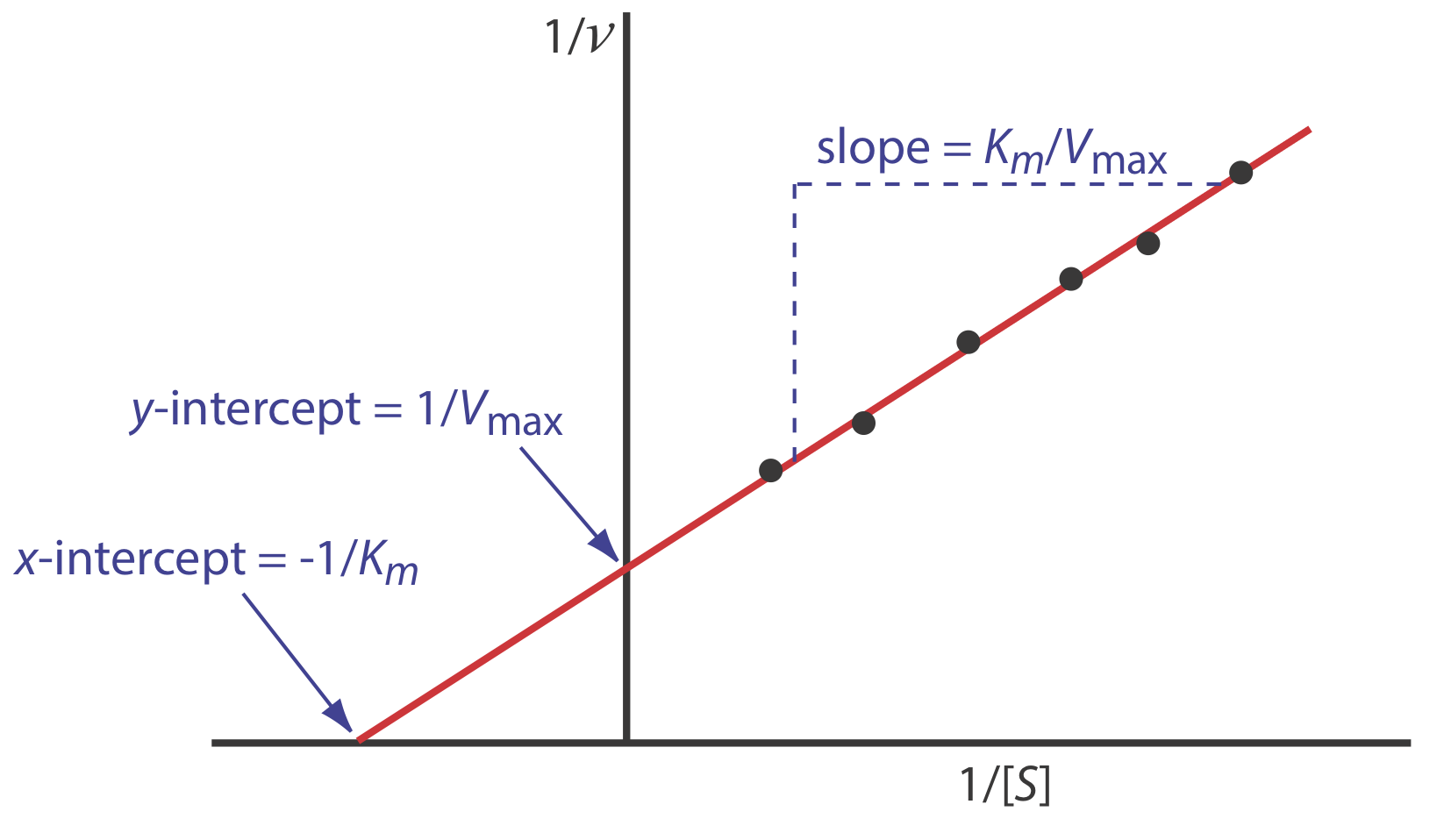
En el Capítulo 5 notamos que cuando se enfrenta a un modelo no lineal —y la Ecuación\ ref {13.25} es un ejemplo de un modelo no lineal—puede ser posible reescribir la ecuación en forma lineal. Esta es la estrategia utilizada aquí. Linealizar un modelo no lineal no está exento de limitaciones, dos de las cuales merecen una breve mención. Primero, debido a que es poco probable que tengamos datos para grandes concentraciones de sustrato, no tendremos muchos puntos de datos para valores pequeños de 1/ [S]. Como resultado, nuestra determinación del valor de la intercepción y se basa en una extrapolación significativa. Segundo, tomar el recíproco de la tasa distorsiona el error experimental de manera que puede invalidar los supuestos de una regresión lineal. La regresión no lineal proporciona un método más riguroso para ajustar la ecuación\ ref {13.25} a los datos experimentales. Los detalles están más allá del nivel de este libro de texto, pero puede consultar a Massart, D. L.; Vandeginste, B. G. M.; Buydens, L. M. C. De Jong, S.; Lewi, P. J.; Smeyers-Verbeke, J. “Regresión no lineal”, que es el Capítulo 11 del Manual de Quimiometría y Cualimetría: Parte A, Elsevier: Amsterdam, 1997, para más detalles. El algoritmo simplex descrito en el Capítulo 14 de este texto también se puede utilizar para ajustar una ecuación no lineal a datos experimentales.

Ejemplo 13.2.6

La reacción entre el mononucleótido de nicotineamida y el ATP para formar dinucleótido de nicotinamida-adenina y pirofosfato es catalizada por la enzima nicotinamida mononucleótido adeniltransferasa [(a) Atkinson, M. R.; Jackson, J. F.; Morton, R. K. Biochem. J. 1961, 80, 318—323; b) Wilkinson, G. N. Biochem. J. 1961, 80, 324—332]. La siguiente tabla proporciona datos típicos obtenidos a un pH de 4.95. El sustrato, S, es mononucleótido de nicotinamida y la velocidad inicial, v, es el μmol de dinucleótido nicotinamida-adenina formado en un periodo de reacción de 3 min.

[S] (mM)	v (µmol)	[S] (mM)	v (µmol)
0.138	0.148	0.560	0.324
0.220	0.171	0.766	0.390
0.291	0.234	1.460	0.493

Determinar valores para V _max y K _m.

Solución

La Figura 13.2.11 muestra la gráfica Lineweaver—Burk para estos datos y la ecuación de regresión result-ng. Usando la intersección y, calculamos V _max como

\[V_{\max }=\frac{1}{y\text {-intercept }}=\frac{1}{1.708 \: \mu \mathrm{mol}^{-1}}=0.585 \: \mu \mathrm{mol} \nonumber\]

y usando la pendiente encontramos que K _m es

\[K_{m} = \text {slope} \times V_{\max}=0.7528 \: \mu \mathrm{mol}^{-1} \mathrm{mM} \times 0.585 \: \mu \mathrm{mol}=0.440 \mathrm{ mM} \nonumber\]

Figura 13.2.11 . Lineweaver—Gráfica de Burk y ecuación de regresión para los datos del Ejemplo 13.2.6 .

Ejercicio 13.2.3

Los siguientes datos fueron recolectados durante la oxidación del catecol (el sustrato) a o-quinona por la enzima o-difenil oxidasa. A la reacción le siguió el monitoreo del cambio en la absorbancia a 540 nm. Los datos de este ejercicio están adaptados de jkimball.

[catecol] (mM):	0.3	0.6	1.2	4.8
tasa (\(\Delta\)AU/min):	0.020	0.035	0.048	0.081

Contestar

La siguiente figura muestra la gráfica Lineweaver—Burk y la ecuación para los datos. La intercepción y de 9.974 min/ (\(\Delta\)AU equivale a 1/ V _max; así, V _max es 0.10\(\Delta\) AU/min. La pendiente de 11.89 min/ (\ Delta\) AU•mm es equivalente a K _m/V _max; así, K _m es 1.2 mM.

Mecanismos elucidantes para la Inhibición de Catálisis Enzimática

Cuando un inhibidor interactúa con una enzima disminuye la eficiencia catalítica de la enzima. Un inhibidor irreversible se une covalentemente al sitio activo de la enzima, produciendo una pérdida permanente en la eficiencia catalítica incluso si disminuimos la concentración del inhibidor. Un inhibidor reversible forma un complejo no covalente con la enzima, resultando en una disminución temporal de la eficiencia catalítica. Si eliminamos el inhibidor, la eficiencia catalítica de la enzima vuelve a su nivel normal.

Existen varias vías para la unión reversible de un inhibidor y una enzima, como se muestra en la Figura 13.2.12 . En la inhibición competitiva el sustrato y el inhibidor compiten por el mismo sitio activo en la enzima. Debido a que el sustrato no puede unirse a un complejo enzima-inhibidor, EI, la eficiencia catalítica de la enzima para el sustrato disminuye. Con inhibición no competitiva, el sustrato y el inhibidor se unen a diferentes sitios activos en la enzima, formando una enzima-sustrato-inhibidor o complejo ESI. La formación de un complejo ESI disminuye la eficiencia catalítica porque solo el complejo enzima-sustrato reacciona para formar el producto. Finalmente, en la inhibición no competitiva el inhibidor se une al complejo enzima-sustrato, formando un complejo ESI inactivo.

Figura 13.2.12 . Mecanismos para la inhibición reversible de la catálisis enzimática. E: enzima, S: sustrato, P: producto, I: inhibidor, ES: complejo enzima-sustrato, EI: enzima-inhibidor com- plex, ESI: complejo enzima-sustrato-inhibidor.

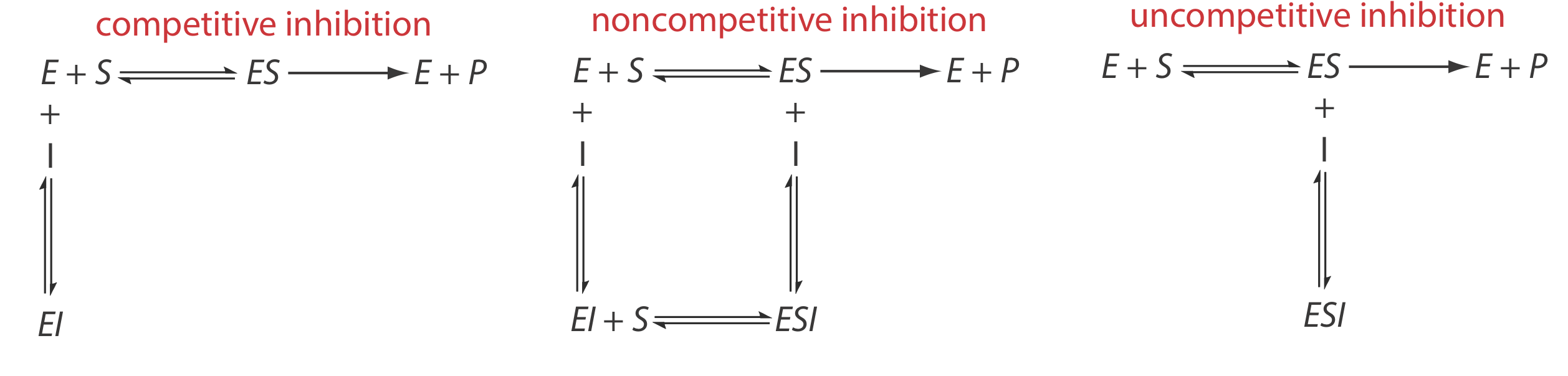
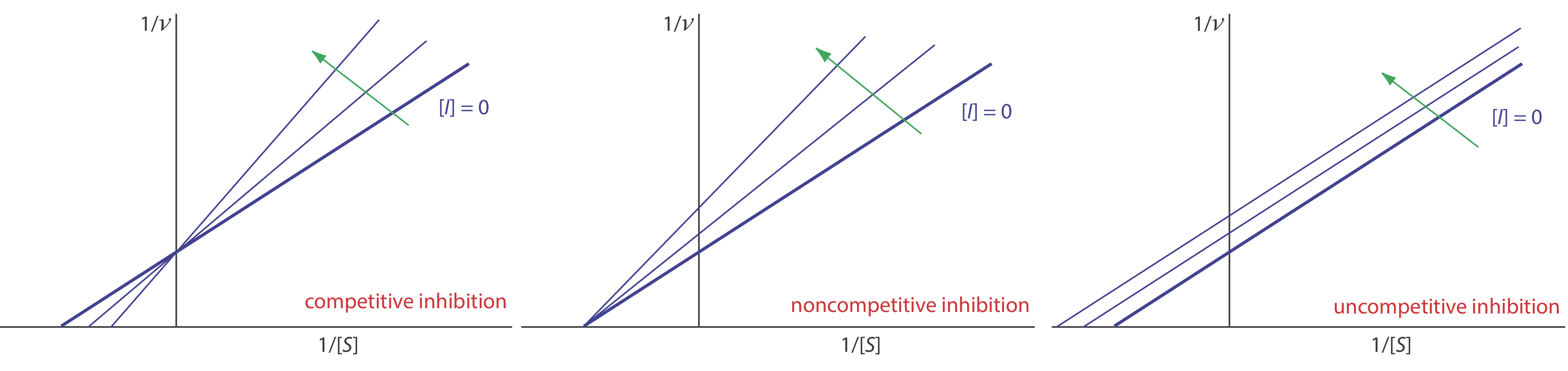
Podemos identificar el tipo de inhibición reversible observando cómo un cambio en la concentración del inhibidor afecta la relación entre la velocidad de reacción y la concentración del sustrato. Como se muestra en la Figura 13.2.13 , cuando mostramos datos cinéticos usando como gráfica Lineweaver-Burk es fácil determinar qué mecanismo está vigente. Por ejemplo, un aumento en la pendiente, una disminución en la intercepción x y ningún cambio en la intercepción y indica inhibición competitiva. Debido a que la unión del inhibidor es reversible, aún podemos obtener la misma velocidad máxima, por lo tanto, el valor constante para la intercepción y, agregando suficiente sustrato para desplazar completamente al inhibidor. Debido a que toma más sustrato, el valor de K _m aumenta, lo que explica el incremento en la pendiente y la disminución en el valor de la intercepción x.

Figura 13.2.13 . Lineweaver—Burk grafica para inhibición competitiva, inhibición no competitiva e inhibición no competitiva. La línea azul gruesa en cada parcela muestra el comportamiento cinético en ausencia de inhibidor, y las líneas azules delgadas en cada parcela muestran el cambio en el comportamiento para concentraciones crecientes del inhibidor. En cada parcela, la concentración del inhibidor aumenta en la dirección de la flecha verde.

Ejemplo 13.2.7

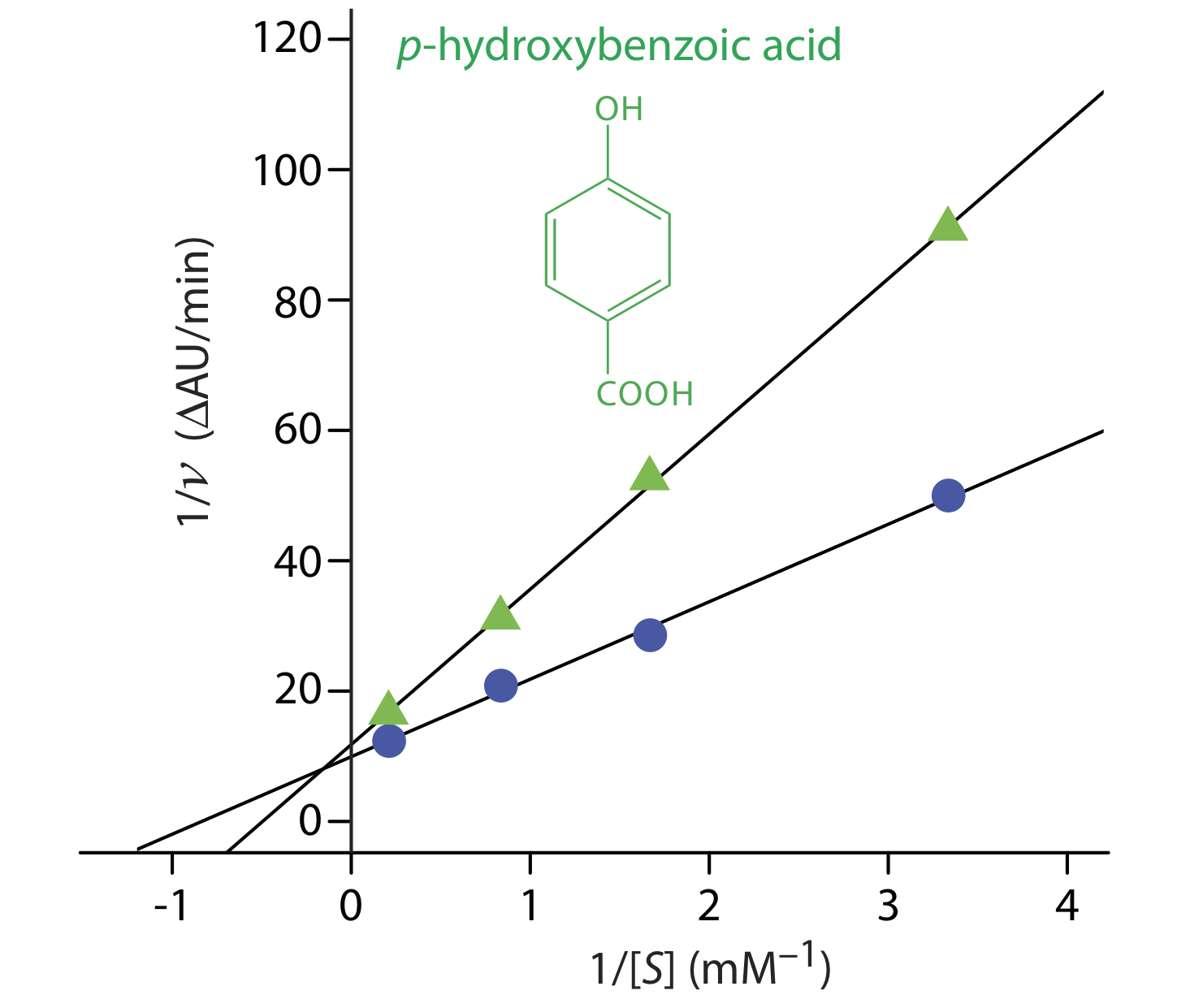
El ejercicio 13.2.3 proporciona datos cinéticos para la oxidación del catecol (el sustrato) a o-quinona por la enzima o -difenil oxidasa en ausencia de un inhibidor. Los siguientes datos adicionales están disponibles cuando la reacción se realiza en presencia de ácido p-hidroxibenzoico, PBHA. ¿El PBHA es un inhibidor de esta reacción y, de ser así, qué tipo de inhibidor es? Los datos de este ejercicio están adaptados de jkimball.

[catecol] (mM):	0.3	0.6	1.2	4.8
tasa (\(\Delta\)AU/min):	0.011	0.019	0.022	0.060

Solución

La Figura 13.2.14 muestra la gráfica Lineweaver—Burk resultante para los datos en Ejercicio 13.2.3 y Ejemplo 13.2.7 . Aunque las dos intersecciones y no son idénticas en valor, el resultado de la incertidumbre en la medición de las tasas, la gráfica sugiere que PBHA es un inhibidor competitivo para la reacción de la enzima con catecol.

Figura 13.2.14 . Lineweaver: Burk traza los datos en el Ejercicio 13.2.3 y Ejemplo 13.2.7 .

Ejercicio 13.2.4

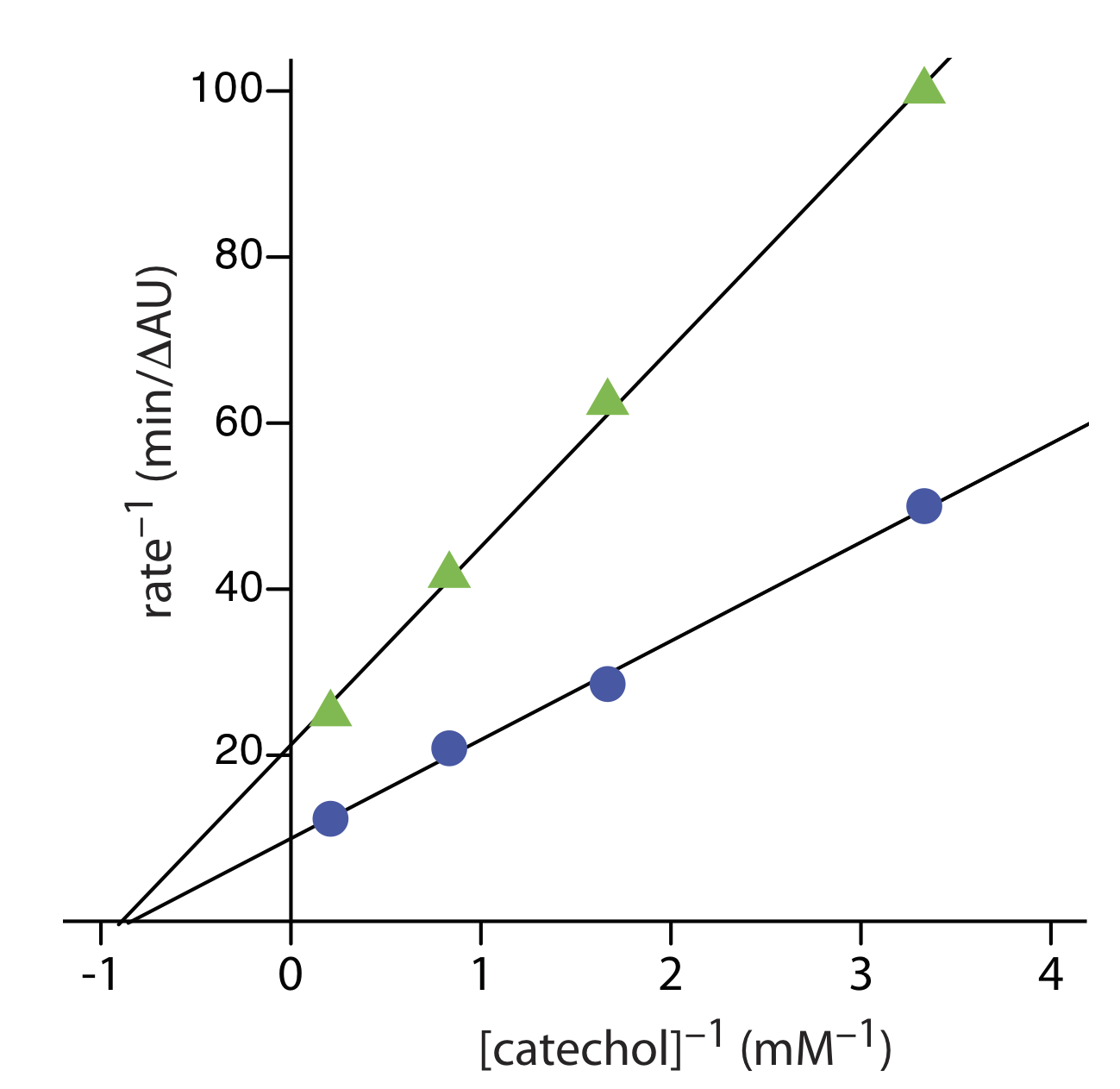
El ejercicio 13.2.3 proporciona datos cinéticos para la oxidación del catecol (el sustrato) a o-quinona por la enzima o -difenil oxidasa en ausencia de un inhibidor. Los siguientes datos adicionales están disponibles cuando la reacción se lleva a cabo en presencia de feniltiourea. ¿La feniltiourea es un inhibidor de esta reacción y, de ser así, qué tipo de inhibidor es? Los datos de este ejercicio están adaptados de jkimball.

[catecol] (mM):	0.3	0.6	1.2	4.8
tasa (\(\Delta\)AU/min):	0.010	0.016	0.024	0.040

Contestar

La siguiente figura muestra las gráficas Lineweaver—Burk para los dos conjuntos de datos. Las intercepciones x casi idénticas sugieren que la feniltiourea es un inhibidor no competitivo.

Evaluación de Métodos Cinéticos Químicos

Escala de Operación

El límite de detección para un método cinético químico varía de componentes menores a componentes de ultratraza, y está determinado por dos factores: la velocidad de la reacción y la técnica instrumental utilizada para monitorear la velocidad. Debido a que la señal es directamente proporcional a la velocidad de la reacción, una reacción más rápida generalmente resulta en un límite de detección más bajo. Siendo iguales todos los demás factores, los límites de detección son menores para las reacciones catalíticas que para las reacciones no catalíticas. No es sorprendente que algunos de los primeros métodos cinéticos químicos aprovecharan las reacciones catalíticas. Por ejemplo, los niveles de ultratraza de Cu (<1 ppb) se determinan midiendo su efecto catalítico sobre la reacción redox entre hidroquinona y H ₂ O ₂.

En ausencia de un catalizador, la mayoría de los métodos cinéticos químicos para compuestos orgánicos utilizan reacciones con velocidades relativamente lentas, lo que limita el análisis a analitos traza menores y mayores concentraciones. Los métodos cinéticos químicos no catalíticos para compuestos inorgánicos que utilizan reacciones de complejación metal-ligando pueden ser rápidos o lentos, con límites de detección que van desde trazas hasta analitos menores.

El segundo factor que influye en el límite de detección de un método es la instrumentación utilizada para monitorear el progreso de la reacción. La mayoría de las reacciones se controlan espectrofotométricamente o electroquímicamente. La escala de operación para estas técnicas se discuten en el Capítulo 10 y el Capítulo 11.

Precisión

Como se señaló anteriormente, un método cinético químico potencialmente está sujeto a errores mayores que un método de equilibrio debido al efecto de variables incontroladas o mal controladas, como la temperatura o el pH. Aunque un método cinético químico de cálculo directo puede lograr resultados moderadamente precisos (un error relativo de 1— 5%), la precisión a menudo es mucho peor. Los métodos de ajuste de curvas proporcionan mejoras significativas en la precisión porque utilizan más datos. En un estudio, por ejemplo, la precisión se mejoró en dos órdenes de magnitud —de errores de 500% a 5%— al reemplazar un análisis de cálculo directo por un análisis de ajuste de curva [Pauch, J. B.; Margerum, D. W. Anal. Chem. 1969, 41, 226—232]. Aunque no se discute en este capítulo, los métodos de análisis de datos que incluyen la capacidad de compensar errores experimentales pueden conducir a una mejora significativa en la precisión [(a) Holler, F. J.; Calhoun, R. K.; McLanahan, S. F. Anal. Chem. 1982, 54, 755—761; b) Wentzel, P. D.; Crouch, S. R. Anal. Chem. 1986, 58, 2851—2855; c) Wentzel, P. D.; Crouch, S. R. Anal. Chem. 1986, 58, 2855—2858].

Precisión

La precisión de un método cinético químico está limitada por la relación señal/ruido de la instrumentación utilizada para monitorear el progreso de la reacción. Cuando se utiliza un método integral, una precisión de 1— 2% es rutinariamente posible. La precisión para un método diferencial puede ser algo peor, particularmente si la señal es ruidosa.

Sensibilidad

Podemos mejorar la sensibilidad de un método integral de tiempo fijo de un punto realizando mediciones en condiciones donde la concentración de las especies monitoreadas sea lo más grande posible. Al monitorear la concentración del analito, o la concentración de cualquier otro reactivo, queremos tomar medidas al principio de la reacción antes de que disminuya su concentración. Por otro lado, si elegimos monitorear uno de los productos de la reacción, entonces es mejor tomar medidas en tiempos más largos. Para un método integral de tiempo fijo de dos puntos, podemos mejorar la sensibilidad aumentando la diferencia entre los tiempos t ₁ y t ₂. Como se discutió anteriormente, la sensibilidad de un método de tasa mejora cuando elegimos medir la tasa inicial.

Selectividad

El análisis de compuestos estrechamente relacionados, como se discutió en capítulos anteriores, a menudo se complica por su tendencia a interferir entre sí. Para superar este problema generalmente necesitamos separar el analito y el interferente antes de completar el análisis. Una ventaja de un método cinético químico es que a menudo es posible ajustar las condiciones de reacción para que el analito y el interferente tengan diferentes velocidades de reacción. Si la diferencia en sus respectivas tasas es lo suficientemente grande, entonces una especie reaccionará completamente antes de que la otra especie tenga oportunidad de reaccionar.

La necesidad de analizar múltiples analitos en mezclas complejas es, por supuesto, una de las ventajas de las técnicas de separación cubiertas en el Capítulo 12. Las técnicas cinéticas proporcionan un enfoque alternativo para mezclas simples.

Podemos usar las leyes de tasa integradas apropiadas para encontrar las condiciones necesarias para separar una especie que reacciona más rápido de una especie que reacciona más lentamente. Consideremos un sistema que consiste en un analito, A, y un interferente, B, los cuales muestran cinética de primer orden con un reactivo común. Para evitar una interferencia, las magnitudes relativas de sus constantes de velocidad deben ser suficientemente diferentes. Las fracciones, f, de A y B que permanecen en cualquier momento, t, se definen por las siguientes ecuaciones

\[\left(f_{A}\right)_{t}=\frac{[A]_{t}}{[A]_{0}} \label{13.29}\]

\[\left(f_{B}\right)_{t}=\frac{[B]_{t}}{[B]_{0}} \label{13.30}\]

donde [A] ₀ y [B] ₀ son las concentraciones iniciales de A y B, respectivamente. Reordenando la Ecuación\ ref {13.2} y sustituyendo en Ecuación\ ref {13.29} o Ecuación\ ref {13.30} deja uso con las siguientes dos ecuaciones.

\[\ln \frac{[A]_{t}}{[A]_{0}}=\ln \left(f_{A}\right)_{t}=-k_{A} t \label{13.31}\]

\[\ln \frac{[B]_{t}}{[B]_{0}}=\ln \left(f_{B}\right)_{t}=-k_{B} t \label{13.32}\]

donde k _A y k _B son las constantes de velocidad para A y para B. Dividiendo Ecuación\ ref {13.31} por Ecuación\ ref {13.32} déjanos con

\[\frac{k_{A}}{k_{B}}=\frac{\ln \left(f_{\mathcal{A}}\right)_{t}}{\ln \left(f_{B}\right)_{t}} \nonumber\]

Supongamos que queremos que 99% de A reaccione antes de que reaccione 1% de B. La fracción de A que queda es 0.01 y la fracción de B que queda es 0.99, lo que requiere que

\[\frac{k_{A}}{k_{B}}=\frac{\ln \left(f_{A}\right)_{t}}{\ln \left(f_{B}\right)_{t}}=\frac{\ln (0.01)}{\ln (0.99)}=460 \nonumber\]

la constante de velocidad para A debe ser al menos 460 veces mayor que la de B. Cuando se cumple esta condición podemos determinar la concentración del analito antes de que el interferente comience a reaccionar. Si el analito tiene la reacción más lenta, entonces podemos determinar su concentración después de permitir que el interferente reaccione hasta su finalización.

Este método de ajuste de las velocidades de reacción es útil si necesitamos analizar un analito en presencia de un interferente, pero es poco práctico si tanto A como B son analitos porque la condición que favorece el análisis de A no favorecerá el análisis de B. Por ejemplo, si ajustamos las condiciones para que 99% de A reaccione en 5 s, entonces 99% de B debe reaccionar dentro de 0.01 s si tiene la cinética más rápida, o en 2300 s si tiene la cinética más lenta. La reacción de B es demasiado rápida o demasiado lenta para hacer de este un método analítico útil.

¿Qué hacemos si la diferencia en las constantes de tasa para A y B no son significativamente diferentes? Todavía podemos completar un análisis si podemos monitorear simultáneamente ambas especies. Debido a que tanto A como B reaccionan al mismo tiempo, la forma integrada de la ley de tarifas de primer orden se convierte en

\[C_{t}=[A]_{t}+[B]_{t}=[A]_{0} e^{-k_{A}t}+[B]_{0} e^{-k_{B}t} \label{13.33}\]

donde C _t es la concentración total de A y B en el tiempo, t. Si medimos C _t en los tiempos t ₁ y t ₂, podemos resolver el par resultante de ecuaciones simultáneas para determinar los valores [A] ₀ y [B] ₀. Las constantes de velocidad k _A y k _B se determinan en experimentos separados usando soluciones estándar de A y B.

La ecuación\ ref {13.33} también puede servir como base para un método de ajuste de curvas. Como se muestra en la Figura 13.2.15 , una gráfica de ln (C _t) en función del tiempo consta de dos regiones. En tiempos más cortos la gráfica es curva porque A y B reaccionan simultáneamente. En momentos posteriores, sin embargo, la concentración del componente de reacción más rápida, A, disminuye a cero, y la Ecuación\ ref {13.33} simplifica a

\[C_{t} \approx[B]_{t}=[B]_{0} e^{-k_{B}t} \nonumber\]

Bajo estas condiciones, una parcela de ln (C _t) versus tiempo es lineal. Extrapolando la porción lineal a t = 0 da [B] ₀, con [A] ₀ determinado por diferencia.

Figura 13.2.15 . Determinación cinética de un analito de reacción más lenta, B, en presencia de un analito de reacción más rápida, A. Las constantes de velocidad para los dos analitos son: k _A = 1 min ^—1 y k _B = 0.1 min ^—1.

Ejemplo 13.2.8

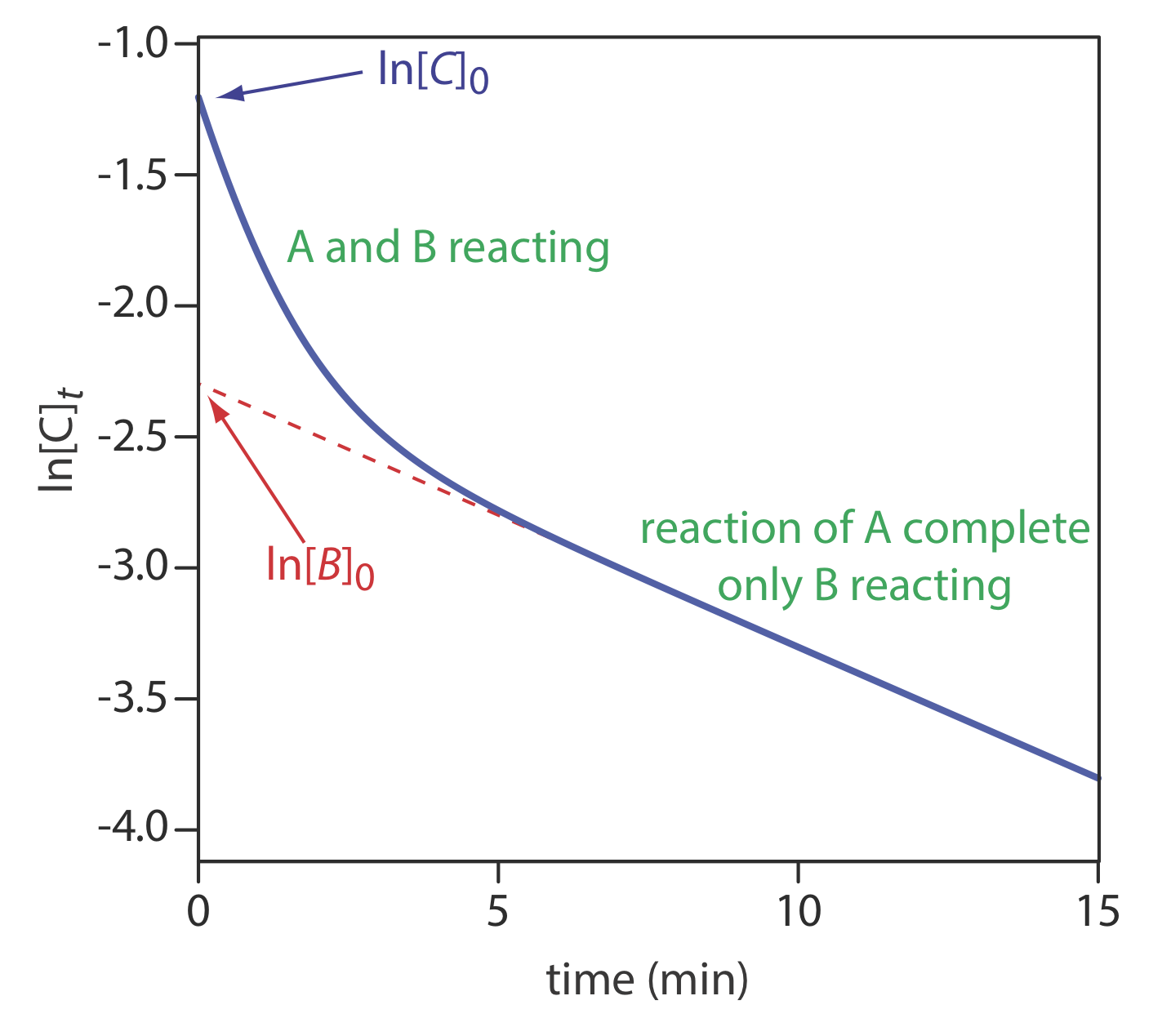
Utilice los datos de la Figura 13.2.15 para determinar las concentraciones de A y B en la muestra original.

Solución

Extrapolando la parte lineal de la curva de nuevo a t = 0 da ln [B] ₀ como —2.3, o a [B] ₀ de 0.10 M. At t = 0, ln [C] ₀ es —1.2, lo que corresponde a un [C] ₀ de 0.30 M. Porque [C] ₀ = [A] ₀ + [B] ₀, la concentración de A en la muestra original es de 0.20 M.

Tiempo, Costo y Equipo

Un método de análisis cinético químico automatizado proporciona un medio rápido para analizar muestras, con rendimientos que van desde varios cientos hasta varios miles de determinaciones por hora. Los costos iniciales de puesta en marcha pueden ser bastante altos porque un análisis automatizado requiere un instrumento dedicado diseñado para satisfacer las necesidades específicas del análisis. Cuando las mediciones se manejan manualmente, un método cinético químico requiere equipos e instrumentación disponibles de forma rutinaria, aunque el rendimiento de la muestra es mucho menor que con un método automatizado.