13.5: Problemas
- Page ID
- 75298
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)1. La ecuación 13.2.18 muestra cómo se determina [A] 0 usando un método integral de tiempo fijo de dos puntos en el que la concentración de A para la reacción de pseudo-primer orden
\[A+R \longrightarrow P \nonumber\]
se mide en los tiempos t 1 y t 2. Derivar una ecuación similar para el caso en el que el producto es monitoreado bajo condiciones de pseudo-primer orden.
2. La concentración de fenilacetato se determina a partir de la cinética de su reacción de hidrólisis de pseudo-primer orden en un tampón de etilamina. Cuando se analiza una solución estándar de fenilacetato 0.55 mM, la concentración de fenilacetato después de 60 s es 0.17 mM. Cuando se analiza una muestra la concentración de fenilacetato que queda después de 60 s es de 0.23 mM. ¿Cuál es la concentración de fenilacetato en la muestra?
3. En presencia de ácido, el yoduro es oxidado por el peróxido de hidrógeno
\[2 \mathrm{I}^{-}(a q)+\mathrm{H}_{2} \mathrm{O}_{2}(a q)+2 \mathrm{H}_{3} \mathrm{O}^{+}(a q) \longrightarrow 4 \mathrm{H}_{2} \mathrm{O}(l)+\mathrm{I}_{2}(a q) \nonumber\]
Cuando I — y H 3 O + están presentes en exceso, podemos usar la cinética de reacción de la reacción, que es de pseudo-primer orden en H 2 O 2, para determinar la concentración de H 2 O 2 siguiendo la producción de I 2 con el tiempo. En un análisis se midió la absorbancia de la solución a 348 nm después de 240 s. El análisis de un conjunto de estándares da los resultados que se muestran a continuación.
| [H 2 O 2] (µM) | absorbancia |
|---|---|
| 100.0 | 0.236 |
| 200.0 | 0.471 |
| 400.0 | 0.933 |
| 800.0 | 1.872 |
¿Cuál es la concentración de H 2 O 2 en una muestra si su absorbancia es 0.669 después de 240 s?
4. La concentración de ácido crómico se determina reduciéndolo en condiciones que son de pseudo-primer orden en analito. Un enfoque es monitorear la absorbancia de la reacción a una longitud de onda de 355 nm. Un estándar de ácido crómico\(5.1 \times 10^{-4}\) M produce absorbancias de 0.855 y 0.709 a los 100 s y 300 s después del inicio de la reacción. Cuando se analiza una muestra en condiciones idénticas, las absorbancias son 0.883 y 0.706. ¿Cuál es la concentración de ácido crómico en la muestra?
5. Malmstadt y Pardue desarrollaron un método de tiempo variable para la determinación de glucosa basado en su oxidación por la enzima glucosa oxidasa [Malmstadt, H. V.; Pardue, H. L. Anal. Chem. 1961 33, 1040—1047]. Para monitorear el progreso de la reacción, se agrega yoduro a las muestras y estándares. El H 2 O 2 producido por la oxidación de la glucosa reacciona con I —, formando I 2 como producto. El tiempo requerido para producir una cantidad fija de I 2 se determina espectrofotométricamente. Se reportaron los siguientes datos para un conjunto de patrones de calibración
| [glucosa] (ppm) | tiempo (s) | ||
|---|---|---|---|
| 5.0 | 146.5 | 150.0 |
149.6 |
| 10.0 | 69.2 | 67.1 |
66.0 |
| 20.0 | 34.8 | 35.0 |
34.0 |
| 30.0 | 22.3 | 22.7 |
22.6 |
| 40.0 | 16.7 | 16.5 | 17.0 |
| 50.0 | 13.3 | 13.3 | 13.8 |
Para verificar el método se analizó una solución estándar de 20.0 ppm de glucosa de la misma manera que los estándares, requiriendo 34.6 s para producir el mismo grado de reacción. Determinar la concentración de glucosa en el estándar y el porcentaje de error para el análisis.
6. Deming y Pardue estudiaron la cinética para la hidrólisis del fosfato de p-nitrofenilo por la enzima fosfatasa alcalina [Deming, S. N.; Pardue, H. L. Anal. Chem. 1971, 43, 192—200]. El progreso de la reacción se monitoreó midiendo la absorbancia de p-nitrofenol, que es uno de los productos de la reacción. Una gráfica de la velocidad de reacción (con unidades de μmol mL—1 seg-1) versus el volumen, V, en mililitros de un estándar de calibración sérica que contenía la enzima, arrojó una línea recta con la siguiente ecuación.
\[\text { rate } = 2.7 \times 10^{-7} \mu \text{mol } \mathrm{mL}^{-1} \text{ s}^{-1}+\left(3.485 \times 10^{-5} \mu \text{mol } \mathrm{mL}^{-2} \text{ s}^{-1}\right) V \nonumber\]
Se analiza una muestra de suero de 10.00-mL, produciendo una tasa de\(6.84 \times 10^{-5}\) μmol mL —1 seg —1. ¿Cuánto más diluida está la enzima en la muestra de suero que en el estándar de calibración de suero?
7. Se recogieron los siguientes datos para una reacción conocida por ser de pseudo-primer orden en el analito, A, durante el tiempo en que se monitoriza la reacción.
| tiempo (s) | [A] t (mM) |
|---|---|
| 2 |
1.36 |
| 4 |
1.24 |
| 6 |
1.12 |
| 8 |
1.02 |
| 10 | 0.924 |
| 12 | 0.838 |
| 14 | 0.760 |
| 16 | 0.690 |
| 18 | 0.626 |
| 20 | 0.568 |
¿Cuál es la constante de velocidad y la concentración inicial de analito en la muestra?
8. La enzima acetilcolinesterasa cataliza la descomposición de la acetilcolina a colina y ácido acético. Bajo un conjunto dado de condiciones la enzima tiene un K m de\(9 \times 10^{-5}\) M y un k 2 de\(1.4 \times 10^4\) s —1. ¿Cuál es la concentración de acetilcolina en una muestra si la velocidad de reacción es de 12.33 μM s —1 en presencia de la enzima\(6.61 \times 10^{-7}\) M? Se puede suponer que la concentración de acetilcolina es significativamente menor que K m.
9. La enzima fumarasa cataliza la adición estereoespecífica de agua al fumarato para formar l-malato. Una solución estándar de fumarasa 0.150 μM tiene una velocidad de reacción de 2.00 μM min —1 en condiciones en las que la concentración del sustrato es significativamente mayor que K m. La velocidad de reacción para una muestra en idénticas condiciones es de 1.15 mM min —1. ¿Cuál es la concentración de fumarasa en la muestra?
10. La enzima ureasa cataliza la hidrólisis de la urea. La velocidad de esta reacción se determina para una serie de soluciones en las que se cambia la concentración de urea mientras se mantiene una concentración fija de ureasa de 5.0 mM. Se obtienen los siguientes datos.
| [urea] (µM) | tasa (µM s —1) |
|---|---|
|
0.100 |
6.25 |
| 0.200 | 12.5 |
| 0.300 | 18.8 |
| 0.400 | 25.0 |
| 0.500 | 31.2 |
| 0.600 | 37.5 |
| 0.700 | 43.7 |
| 0.800 | 50.0 |
| 0.900 | 56.2 |
| 1.00 | 62.5 |
Determinar los valores de V max, k 2 y K m para la ureasa.
11. Para estudiar el efecto de un inhibidor enzimático se miden V max y K m para varias concentraciones de inhibidor. A medida que aumenta la concentración del inhibidor, V max permanece esencialmente constante, pero el valor de K m aumenta. ¿Qué mecanismo de inhibición enzimática está vigente?
12. En el caso de la inhibición competitiva, el equilibrio entre la enzima, E, el inhibidor, I y el complejo enzima-inhibidor, EI, se describe por la constante de equilibrio K EI. Demostrar que para la inhibición competitiva la ecuación para la velocidad de reacción es
\[\frac{d[P]}{d t}=\frac{V_{\max }[S]}{K_{m}\left\{1+\left([I] / K_{E l}\right)\right\}+[S]} \nonumber\]
donde K I es la constante de formación para el complejo EI
\[E+I \rightleftharpoons E I \nonumber\]
Se puede asumir que k 2 << k —1.
13. Los analitos A y B reaccionan con un reactivo común R con cinética de primer orden. Si 99.9% de A debe reaccionar antes de que 0.1% de B haya reaccionado, ¿cuál es la relación mínima aceptable para sus respectivas constantes de velocidad?
14. Se analiza simultáneamente una mezcla de dos analitos, A y B, monitoreando su concentración combinada, C = [A] + [B], en función del tiempo cuando reaccionan con un reactivo común. Se sabe que tanto A como B siguen cinéticas de primer orden con el reactivo, y se sabe que A reacciona más rápido que B. Dados los datos de la siguiente tabla, determinar las concentraciones iniciales de A y B, y las constantes de velocidad de primer orden, k A y k B.
| tiempo (min) | [C] (mM) |
|---|---|
| 1 | 0.313 |
| 6 | 0.200 |
| 11 | 0.136 |
| 16 | 0.098 |
| 21 | 0.074 |
| 26 | 0.058 |
| 31 | 0.047 |
| 36 | 0.038 |
| 41 | 0.032 |
| 46 | 0.027 |
| 51 | 0.023 |
| 56 | 0.019 |
| 61 | 0.016 |
| 66 | 0.014 |
| 71 | 0.012 |
15. En el Cuadro 13.3.1 se proporciona una lista de varios isótopos utilizados como trazadores. También se enumeran las vidas medias de estos isótopos. ¿Cuál es la constante de velocidad para la desintegración radiactiva de cada isótopo?
16. 60 Co es un isótopo de larga vida (t 1/2 = 5.3 año) frecuentemente utilizado como radiotrazador. La actividad en una muestra de 5.00-mL de una solución de 60 Co es\(2.1 \times 10^7\) desintegraciones/seg. ¿Cuál es la concentración molar de 60 Co en la muestra?
17. La concentración de Ni en una nueva aleación se determina mediante un análisis de activación de neutrones. Una muestra de 0.500-g de la aleación y una muestra de 1.000-g de una aleación estándar que es 5.93% p/p de Ni se irradian con neutrones en un reactor nuclear. Cuando se completa la irradiación, la muestra y el patrón se dejan enfriar y se miden sus actividades de rayos gamma. Dado que la actividad es 1020 cpm para la muestra y 3540 cpm para el estándar, determinar el% p/p de Ni en la aleación.
18. El contenido de vitamina B 12 de una tableta multivitamínica se determina mediante el siguiente procedimiento. Una muestra de 10 comprimidos se disuelve en agua y se diluye a volumen en un matraz aforado de 100 ml. Se retira una porción de 50.00-mL y se agregan 0.500 mg de vitamina B 12 radiactiva que tiene una actividad de 572 cpm como trazador. La muestra y el trazador se homogeneizan y la vitamina B 12 se aísla y purifica, produciendo 18.6 mg con una actividad de 361 cpm. Calcular los miligramos de vitamina B 12 en una tableta multivitamínica.
19. La muestra más antigua que se puede fechar por 14 C es aproximadamente 30 000 año. ¿Qué porcentaje de los 14 C queda después de este lapso de tiempo?
20. Potasio-argón La datación se basa en la desintegración nuclear de 40 K a 40 Ar (t 1/2 =\(1.3 \times 10^9\) año). Si no hay 40 Ar originalmente presente en la roca, y si 40 Ar no puede escapar a la atmósfera, entonces las cantidades relativas de 40 K y 40 Ar pueden usarse para determinar la edad de la roca. Cuando se analiza una muestra de roca de 100.0-mg se encuentra que contiene\(4.63 \times 10^{-6}\) mol de 40 K y\(2.09 \times 10^{-6}\) mol 40 Ar. ¿Qué edad tiene la muestra de roca?
21. La actividad en estado estacionario para 14 C en una muestra es de 13 cpm por gramo de carbono. Si el conteo se limita a 1 hr, ¿qué masa de carbono se necesita para dar un porcentaje de desviación estándar relativa del 1% para la actividad de la muestra? ¿Cuánto tiempo debemos monitorear la desintegración radiactiva de una muestra de 0.50-g de carbono para dar un porcentaje de desviación estándar relativa de 1.0% para la actividad?
22. Para mejorar la sensibilidad de un análisis FIA, puede realizar cualquiera de las siguientes acciones: inyectar un mayor volumen de muestra, aumentar el caudal, disminuir la longitud y el diámetro del tubo del colector o fusionar canales separados antes de inyectar la muestra. Para cada acción, explique por qué conduce a una mejora en la sensibilidad.
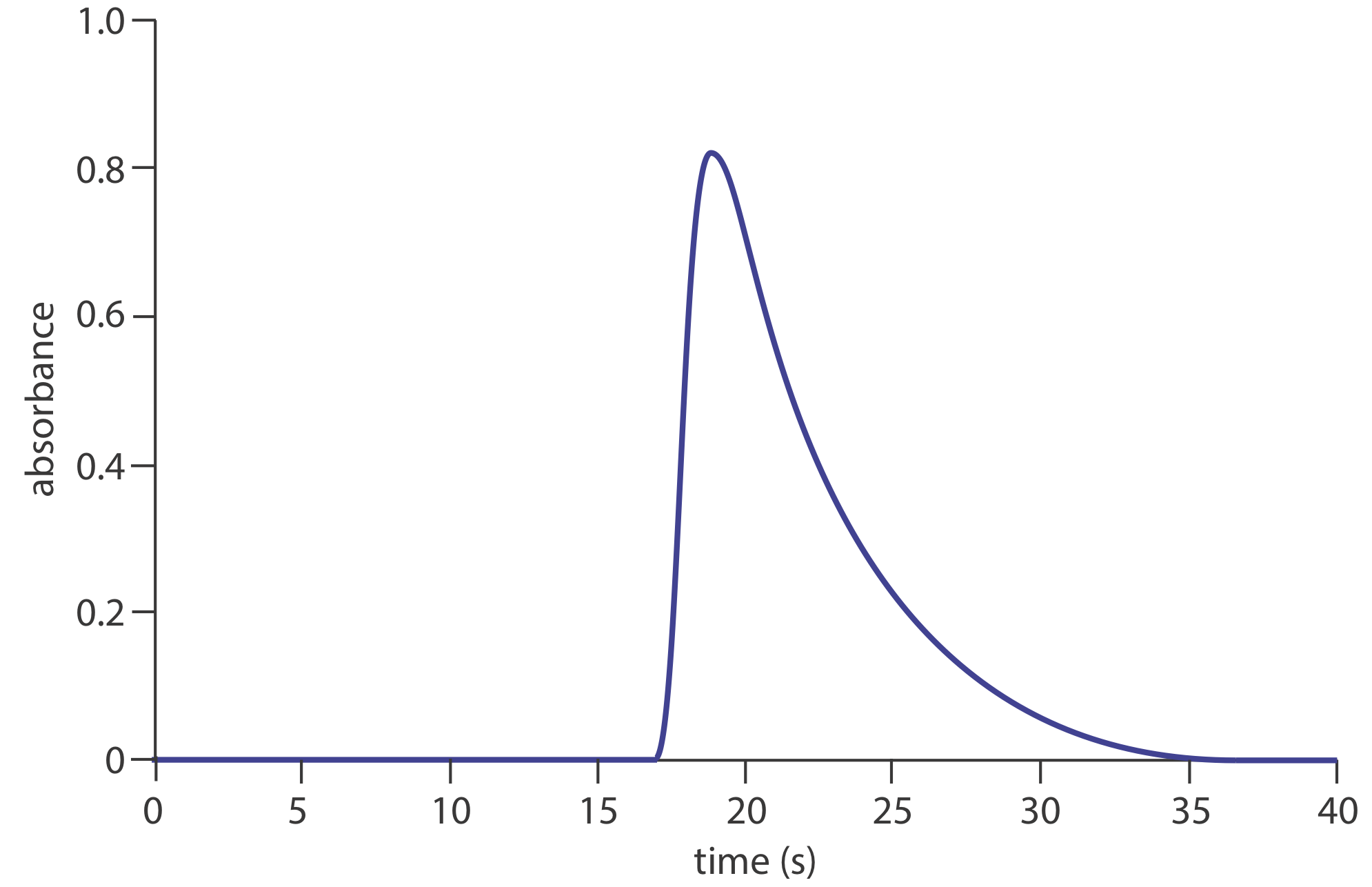
23. En la siguiente figura se muestra un fiagrama para una solución de 50.0-ppm\(\text{PO}_4^{3-}\) utilizando el método del Método Representativo 13.4.1. Determinar los valores para h, t a, T, t ′\(\Delta t\), y T ′. ¿Cuál es la sensibilidad de este método FIA, asumiendo una relación lineal entre absorbancia y concentración? ¿Cuántas muestras se pueden analizar por hora?
24. Un método sensible para el análisis de inyección de flujo de Cu 2 + se basa en su capacidad para catalizar la oxidación de di-2-piridil cetona hidrazona (DPKH) [Lazaro, F.; Luque de Castro, M. D.; Valcárcel, M. Analyst, 1984, 109, 333—337]. El producto de la reacción es fluorescente y se utiliza para generar una señal cuando se usa un fluorímetro como detector. El rendimiento de la reacción es máximo cuando la solución se basifica con NaOH. La fluorescencia, sin embargo, es mayor en presencia de HCl. Dibuje un colector FIA apropiado para este análisis.
25. La concentración de cloruro en el agua de mar se determina mediante un análisis de inyección de flujo. El análisis de un conjunto de estándares de calibración da los siguientes resultados.
| [Cl —] (ppm) | absorbancia | [Cl —] (ppm) | absorbancia |
|---|---|---|---|
|
5.00 |
0.057 | 40.00 | 0.478 |
| 10.00 | 0.099 | 50.00 | 0.594 |
| 20.00 | 0.230 | 75.00 | 0.840 |
| 30.00 | 0.354 |
Una muestra de 1.00-mL de agua de mar se coloca en un matraz aforado de 500 mL y se diluye a volumen con agua destilada. Cuando se inyecta en el analizador de inyección de flujo se mide una absorbancia de 0.317. ¿Cuál es la concentración de Cl — en la muestra?
26. Ramsing y sus colaboradores desarrollaron un método FIA para valoraciones ácido-base utilizando una corriente portadora que es NaOH\(2.0 \times 10^{-3}\) M y que contiene el indicador ácido-base azul de bromotimol [Ramsing, A. U.; Ruzicka, J.; Hansen, E. H. Anal. Chim. Acta 1981, 129, 1—17]. Se inyectaron soluciones estándar de HCl, y se\(\Delta t\) midieron los siguientes valores de a partir de los fiagramas resultantes.
| [HCl] (M) | \(\Delta t\)(s) | [HCl] (M) | \(\Delta t\)(s) |
|---|---|---|---|
| 0.008 | \ (\ Delta t\) (s) ">3.13 | 0.080 | \ (\ Delta t\) (s)” class="lt-chem-151886">
7.71 |
| 0.010 | \ (\ Delta t\) (s) ">3.59 | 0.100 | \ (\ Delta t\) (s)” class="lt-chem-151886">
8.13 |
| 0.020 | \ (\ Delta t\) (s) ">5.11 | 0.200 | \ (\ Delta t\) (s)” class="lt-chem-151886">
9.27 |
| 0.040 | \ (\ Delta t\) (s) ">6.39 | 0.400 | \ (\ Delta t\) (s)” class="lt-chem-151886">
10.45 |
| 0.060 | \ (\ Delta t\) (s) ">7.06 | 0.600 | \ (\ Delta t\) (s) ">11.40 |
Se analiza cinco veces una muestra con una concentración desconocida de HCl, dando valores de 7.43, 7.28, 7.41, 7.37 y 7.33 s para\(\Delta t\). Determinar la concentración de HCl en la muestra.
27. Milardovíc y colegas utilizaron un método de análisis de inyección de flujo con un biosensor amperométrico para determinar la concentración de glucosa en sangre [Milardović, S.; Kruhak, I.; Ivekovic, D.; Rumenjak, V.; Tkalcec, M.; Grabaric, B. S. Anal. Chim. Acta 1997, 350, 91—96]. Dado que una muestra de sangre que es 6.93 mM en glucosa tiene una señal de 7.13 nA, ¿cuál es la concentración de glucosa en una muestra de sangre si su señal es de 11.50 nA?
28. Fernández-abedul y Costa-García desarrollaron un método FIA para determinar la cocaína en muestras usando un detector amperometrico [Fernández-Abedul, M; Costa-García, A. Anal. Chim. Acta 1996, 328, 67—71]. Se recolectaron las siguientes señales (unidades arbitrarias) para 12 inyecciones replicadas de una muestra\(6.2 \times 10^{-6}\) M de cocaína, C 17 H 21 NO 4.
|
24.5 |
24.1 |
24.1 |
|
23.8 |
23.9 |
25.1 |
|
23.9 |
24.8 | 23.7 |
| 23.3 | 23.2 | 23.2 |
a) ¿Cuál es la desviación estándar relativa para esta muestra?
b) Se dispone de los siguientes datos de calibración
| [cocaína] (µM) | señal (unidades arb.) |
|---|---|
|
0.18 |
0.8 |
|
0.36 |
2.1 |
|
0.60 |
2.4 |
|
0.81 |
3.2 |
|
1.0 |
4.5 |
|
2.0 |
8.1 |
|
4.0 |
14.4 |
|
6.0 |
21.6 |
|
8.0 |
27.1 |
| 10.0 | 32.9 |
En un análisis típico se disuelve una muestra de 10.0-mg en agua y se diluye a volumen en un matraz aforado de 25 ml. Una alícuota de 125 ml se transfiere a un matraz aforado de 25 ml y se diluye a volumen con un tampón de pH 9. Cuando se inyecta en el aparato de inyección de flujo se obtiene una señal de 21.4 (unidades arb.). ¿Cuál es el% w/w de cocaína en la muestra?
29. Holman, Christian y Ruzicka describieron un método FIA para determinar la concentración de H 2 SO 4 en disolventes no acuosos [Holman, D. A.; Christian, G. D.; Ruzicka, J. Anal. Chem. 1997, 69, 1763—1765]. Las perlas de agarosa (22—45 mm de diámetro) con un indicador ácido-base unido se empapan en NaOH y se inmovilizan en la celda de flujo del detector. Muestras de H 2 SO 4 en n-butanol se inyectan en la corriente portadora. A medida que una muestra pasa a través de la celda de flujo, se produce una reacción ácido-base entre H 2 SO 4 y NaOH. El punto final de la reacción de neutralización es señalado por un cambio en el color del indicador unido y se detecta espectrofotométricamente. El volumen de elución necesario para alcanzar el punto final de la titulación es inversamente proporcional a la concentración de H 2 SO 4; por lo tanto, una gráfica de volumen de punto final versus [H 2 SO 4] —1 es lineal. Los siguientes datos son típicos de los obtenidos mediante un conjunto de estándares externos.
| [H 2 SO 4] (mM) | volumen de punto final (mL) |
|---|---|
|
0.358 |
0.266 |
|
0.436 |
0.227 |
|
0.560 |
0.176 |
|
0.752 |
0.136 |
| 1.38 | 0.075 |
| 2.98 | 0.037 |
| 5.62 | 0.017 |
¿Cuál es la concentración de H 2 SO 4 en una muestra si su volumen de punto final es de 0.157 mL?


