13.3: Radioquímica
- Page ID
- 75299
Los átomos que tienen el mismo número de protones pero un número diferente de neutrones son isótopos. Para identificar un isótopo usamos la notación\({}_Z^A E\), donde E es el símbolo atómico del elemento, Z es el número atómico del elemento y A es el número de masa atómica del elemento. Aunque los diferentes isótopos de un elemento tienen las mismas propiedades químicas, sus propiedades nucleares no son idénticas. La diferencia más importante entre los isótopos es su estabilidad. La configuración nuclear de un isótopo estable permanece constante con el tiempo. Los isótopos inestables, sin embargo, se desintegran espontáneamente, emitiendo partículas radiactivas a medida que se transforman en una forma más estable.
El número atómico de un elemento, Z, es igual al número de protones y su masa atómica, A, es igual a la suma del número de protones y neutrones. Representamos un isótopo de carbono-13\(_{6}^{13} \text{C}\) porque el carbono tiene seis protones y siete neutrones. A veces omitimos Z de esta notación, identificando el elemento y el número atómico es repetitivo porque todos los isótopos de carbono tienen seis protones y cualquier átomo que tenga seis protones es un isótopo de carbono. Así, 13 C y C—13 son notaciones alternativas para este isótopo de carbono.
Los tipos más importantes de partículas radiactivas son las partículas alfa, las partículas beta, los rayos gamma y los rayos X. Una partícula alfa,\(\alpha\), es equivalente a un núcleo de helio,\({}_2^4 \text{He}\). Cuando un átomo emite una partícula alfa, el producto en un nuevo átomo cuyo número atómico y número de masa atómica son, respectivamente, 2 y 4 menores que su progenitor inestable. La desintegración del uranio en torio es un ejemplo de emisión alfa.
\[_{92}^{238} \text{U} \longrightarrow _{90}^{234} \text{Th}+\alpha \nonumber\]
Una partícula beta,\(\beta\), viene en una de dos formas. Un negatrón,\(_{-1}^0 \beta\), se produce cuando un neutrón se convierte en protón, aumentando el número atómico en uno, como se muestra aquí para el plomo.
\[_{82}^{214} \mathrm{Pb} \longrightarrow_{83}^{214} \mathrm{Bi} + _{-1}^{0} \beta \nonumber\]
La conversión de un protón en un neutrón da como resultado la emisión de un positrón,\(_{1}^0 \beta\).
\[_{15}^{30} \mathrm{P} \longrightarrow_{14}^{30} \mathrm{Si} + _{1}^{0} \beta \nonumber\]
Un negatrón, que es el tipo más común de partícula beta, es equivalente a un electrón.
La emisión de una partícula alfa o beta a menudo produce un isótopo en un estado inestable y de alta energía. Este exceso de energía se libera como un rayo gamma,\(\gamma\), o como una radiografía. La emisión de rayos gamma y rayos X también puede ocurrir sin la liberación de una partícula alfa o una partícula beta.
Teoría y Práctica
La tasa de desintegración de un isótopo radiactivo, o actividad, sigue la cinética de primer orden
\[A=-\frac{d N}{d t}=\lambda N \label{13.1}\]
donde A es la actividad del isótopo, N es el número de átomos radiactivos presentes en la muestra en el tiempo t, y\(\lambda\) es la constante de desintegración del isótopo. La actividad se expresa como el número de desintegraciones por unidad de tiempo.
Como con cualquier proceso de primer orden, podemos reescribir la Ecuación\ ref {13.1} de forma integrada.
\[N_{t}=N_{0} e^{-\lambda t} \label{13.2}\]
Sustituyendo la ecuación\ ref {13.2} en la ecuación\ ref {13.2} da
\[A=\lambda N_{0} e^{-\lambda t}=A_{0} e^{-\lambda t} \label{13.3}\]
Si medimos la actividad de una muestra en el tiempo t podemos determinar la actividad inicial de la muestra, A 0, o el número de átomos radiactivos originalmente presentes en la muestra, N 0.
Una propiedad característica importante de un isótopo radiactivo es su vida media, t 1/2, que es la cantidad de tiempo requerida para que la mitad de los átomos radiactivos se desintegren. Para la cinética de primer orden, la vida media es
\[t_{1 / 2}=\frac{0.693}{\lambda} \label{13.4}\]
Debido a que la vida media es independiente del número de átomos radiactivos, permanece constante durante todo el proceso de desintegración. Por ejemplo, si el 50% de los átomos radiactivos permanecen después de una vida media, entonces el 25% permanece después de dos semividas, y el 12.5% permanece después de tres semividas.
Supongamos que comenzamos con un N 0 de 1200 átomos Durante la primera vida media, 600 átomos se desintegran y quedan 600. Durante la segunda vida media, 300 de los 600 átomos restantes se desintegran, dejando 300 átomos o 25% de los 1200 átomos originales. De los 300 átomos restantes, solo quedan 150 después de la tercera vida media, o 12.5% de los 1200 átomos originales.
La información cinética sobre un isótopo radiactivo generalmente se da en términos de su vida media porque proporciona una sensación más intuitiva de la estabilidad del isótopo. Saber, por ejemplo, que la constante de decaimiento para\(_{38}^{90}\text{Sr}\) es 0.0247 yr —1 no da una idea inmediata de lo rápido que se desintegra. Por otro lado, saber que su vida media es de 28.1 años deja claro que la concentración de\(_{38}^{90}\text{Sr}\) en una muestra permanece esencialmente constante durante un corto periodo de tiempo.
Instrumentación
Las partículas alfa, las partículas beta, los rayos gamma y los rayos X se miden usando la energía de la partícula para producir un pulso amplificado de corriente eléctrica en un detector. Estos pulsos se cuentan para dar la tasa de desintegración. Hay tres tipos comunes de detectores: detectores llenos de gas, contadores de centelleo y detectores de semiconductores. Un detector lleno de gas consiste en un tubo que contiene un gas inerte, como Ar. Cuando una partícula radiactiva ingresa al tubo ioniza el gas inerte, produciendo un par iónico Ar +/e —. El movimiento del electrón hacia el ánodo y del Ar + hacia el cátodo genera una corriente eléctrica medible. Un contador Geiger es un ejemplo de un detector lleno de gas. Un contador de centelleo utiliza un material fluorescente para convertir partículas radiactivas en fotones fáciles de medir. Por ejemplo, un contador de centelleo en estado sólido consiste en un cristal de NaI que contiene 0.2% de TLi, el cual produce varios miles de fotones por cada partícula radiactiva. Finalmente, en un detector de semiconductores, la adsorción de una sola partícula radiactiva promueve miles de electrones a la banda de conducción del semiconductor, aumentando la conductividad.
Aplicaciones Cuantitativas
En esta sección consideramos tres métodos de análisis radioquímicos cuantitativos comunes: el análisis directo de un isótopo radiactivo mediante la medición de su tasa de desintegración, activación de neutrones y dilución de isótopos.
Análisis directo de analitos radiactivos
La concentración de un isótopo radiactivo de larga vida permanece esencialmente constante durante el período de análisis. Como se muestra en el Ejemplo 13.3.1 , podemos usar la actividad de la muestra para calcular el número de partículas radiactivas en la muestra.
La actividad en una muestra de 10.00-mL de aguas residuales que contiene\(_{38}^{90}\text{Sr}\) es\(9.07 \times 10^6\) desintegraciones/s. ¿Cuál es la concentración molar de\(_{38}^{90}\text{Sr}\) en la muestra? La vida media para\(_{38}^{90}\text{Sr}\) es 28.1 año.
Solución
Resolviendo la ecuación\ ref {13.4} para\(\lambda\), sustituyendo en la ecuación\ ref {13.1}, y resolviendo para N da
\[N=\frac{A \times t_{1 / 2}}{0.693} \nonumber\]
Antes de poder determinar el número de átomos de\(_{38}^{90}\text{Sr}\) en la muestra debemos expresar su actividad y su vida media utilizando las mismas unidades. Convertir la vida media a segundos da t 1/2 como\(8.86 \times 10^8\) s; por lo tanto, hay
\[\frac{\left(9.07 \times 10^{6} \text { disintegrations/s }\right)\left(8.86 \times 10^{8} \text{ s}\right)}{0.693} = 1.16 \times 10^{16} \text{ atoms} _{38}^{90}\text{Sr} \nonumber\]
La concentración de\(_{38}^{90}\text{Sr}\) en la muestra es
\[\frac{1.16 \times 10^{16} \text { atoms } _{38}^{90} \text{Sr}}{\left(6.022 \times 10^{23} \text { atoms/mol }\right)(0.01000 \mathrm{L})} = 1.93 \times 10^{-6} \text{ M } _{38}^{90}\text{Sr} \nonumber\]
El análisis directo de un isótopo radiactivo de corta duración utilizando el método descrito en el Ejemplo 13.3.1 es menos útil porque proporciona solo una medida transitoria de la concentración del isótopo. En su lugar, podemos medir su actividad después de un tiempo transcurrido, t, y usar la Ecuación\ ref {13.3} para calcular N 0.
Análisis de activación de neutrones
Pocos analitos son naturalmente radiactivos. Para muchos analitos, sin embargo, podemos inducir radiactividad irradiando la muestra con neutrones en un proceso llamado análisis de activación de neutrones (NAA). El elemento radiactivo formado por la activación de neutrones se descompone a un isótopo estable al emitir un rayo gamma y, posiblemente, otras partículas nucleares. La tasa de emisión de rayos gamma es proporcional a la concentración inicial del analito en la muestra. Por ejemplo, si colocamos una muestra que contiene no radiactivos\(_{13}^{27}\text{Al}\) en un reactor nuclear y la irradiamos con neutrones, se produce la siguiente reacción nuclear.
\[_{13}^{27} \mathrm{Al}+_{0}^{1} \mathrm{n} \longrightarrow_{13}^{28} \mathrm{Al} \nonumber\]
El isótopo radiactivo de 13 Al tiene un proceso de desintegración característico que incluye la liberación de una partícula beta y un rayo gamma.
\[_{13}^{28} \mathrm{Al} \longrightarrow_{14}^{28} \mathrm{Al}+_{-1}^{0} \beta + \gamma \nonumber\]
Cuando se completa la irradiación, retiramos la muestra del reactor nuclear, permitimos que cualquier interferencia radiactiva de corta duración se descomponga en el fondo y medimos la tasa de emisión de rayos gamma.
La actividad inicial al final de la irradiación depende del número de átomos que estén presentes. Esto, a su vez, es igual a la diferencia entre la tasa de formación para\(_{13}^{28}\text{Al}\) y su tasa de desintegración
donde\(\Phi\) es el flujo de neutrones y\(\sigma\) es la sección transversal de la reacción, o probabilidad de que un\(_{13}^{27}\text{Al}\) núcleo capture un neutrón. Integrando la ecuación\ ref {13.5} durante el tiempo de irradiación, t i, y multiplicando por\(\lambda\) da la actividad inicial, A 0, al final de la irradiación como
\[A_0 = \lambda N_{_{13}^{28}\text{Al}} = \Phi \sigma N_{_{13}^{27}\text{Al}} (1-e^{-kt}) \nonumber\]
Si conocemos los valores de A 0,\(\Phi\),\(\sigma\),\(\lambda\), y t i, entonces podemos calcular el número de átomos de\(_{13}^{27}\text{Al}\) inicialmente presentes en la muestra.
Un enfoque más sencillo es utilizar uno o más estándares externos. Dejando\((A_0)_x\) y\((A_0)_s\) representando la actividad inicial del analito en un estándar desconocido y en un estándar externo,\(w_x\) y dejando y\(w_s\) representando el peso del analito en lo desconocido y en el estándar externo, obtenemos el siguiente par de ecuaciones
\[\left(A_{0}\right)_{x}=k w_{x} \label{13.6}\]
\[\left(A_{0}\right)_{s}=k w_{s} \label{13.7}\]
que podemos resolver para determinar la masa del analito en la muestra.
Como se señaló anteriormente, la emisión de rayos gamma se mide siguiendo un período durante el cual permitimos que los interferentes de corta duración se desintegren en el fondo. Como se muestra en la Figura 13.3.1 , determinamos la actividad inicial de la muestra o del estándar extrapolando una curva de actividad versus tiempo atrás a t = 0. Alternativamente, si irradiamos la muestra y el patrón al mismo tiempo, y si medimos sus actividades al mismo tiempo, entonces podemos sustituir estas actividades por (A 0) x y (A 0) s. Esta es la estrategia utilizada en el siguiente ejemplo.
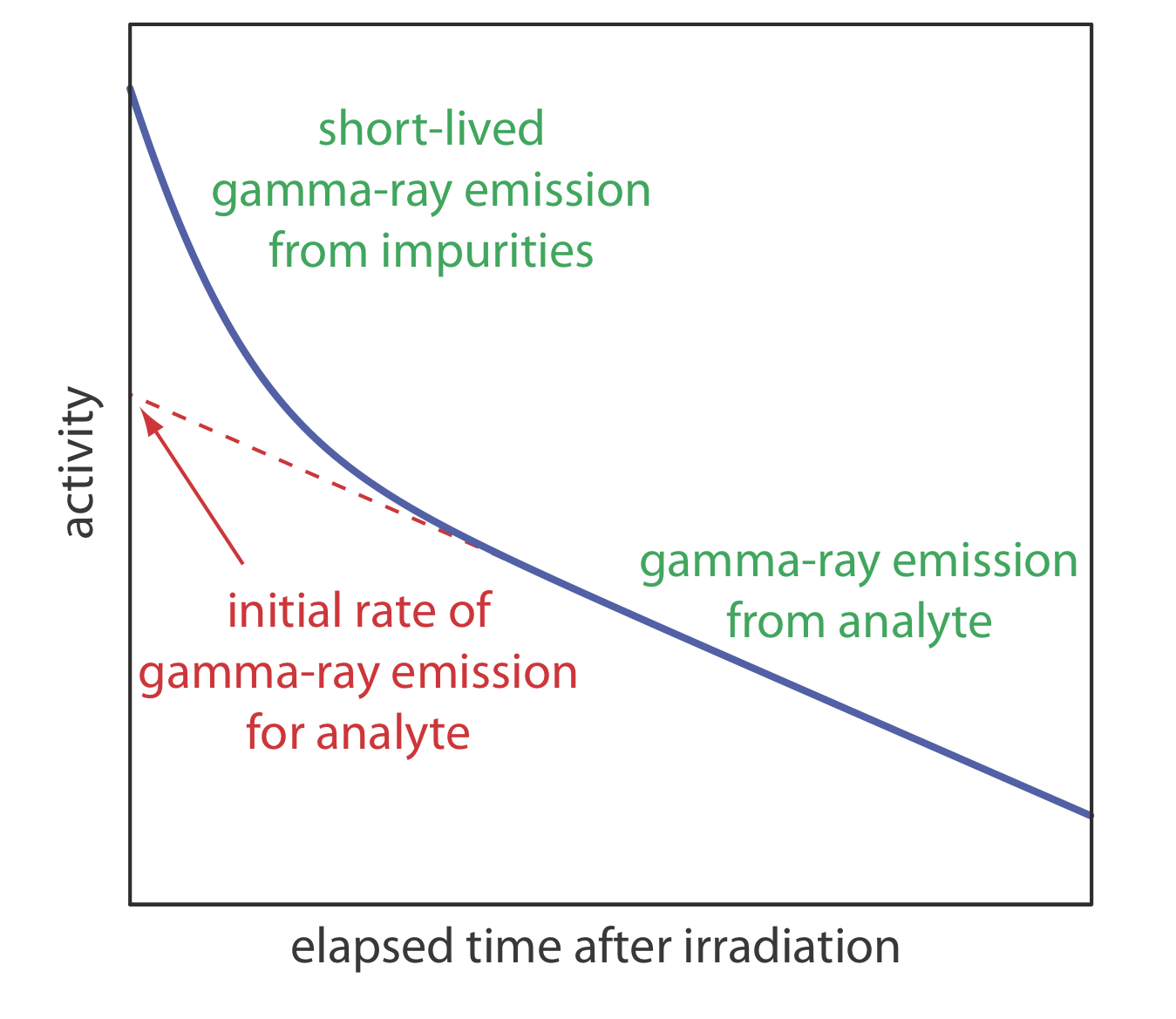
La concentración de Mn en el acero se determina mediante un análisis de activación de neutrones utilizando el método de estándares externos. Una muestra de 1.000-g de una muestra de acero desconocido y una muestra de 0.950 g de un acero estándar que se sabe que contiene 0.463% p/p de Mn se irradian con neutrones durante 10 h en un reactor nuclear. Después de un retraso de 40 min la emisión de rayos gamma es de 2542 cpm (recuentos por minuto) para lo desconocido y 1984 cpm para el estándar externo. ¿Cuál es el% w/w de Mn en la muestra de acero desconocida?
Solución
Combinando ecuaciones\ ref {13.6} y\ ref {13.7} da
\[w_{x}=\frac{A_{x}}{A_{s}} \times w_{s} \nonumber\]
El peso de Mn en el estándar externo es
\[w_{s}=\frac{0.00463 \text{ g } \text{Mn}}{\text{ g } \text { steel }} \times 0.950 \text{ g} \text { steel }=0.00440 \text{ g} \text{ Mn} \nonumber\]
Sustituir en la ecuación anterior da
\[w_{x}=\frac{2542 \text{ cpm}}{1984 \text{ cpm}} \times 0.00440 \text{ g} \text{ Mn}=0.00564 \text{ g} \text{ Mn} \nonumber\]
Debido a que la masa original del acero es de 1.000 g, el% w/w Mn es 0.564%.
Entre las ventajas de la activación de neutrones se encuentran su aplicabilidad a casi todos los elementos de la tabla periódica y que es no destructiva para la muestra. En consecuencia, la NAA es una técnica importante para analizar muestras arqueológicas y forenses, así como obras de arte.
Dilución de isótopos
Otro método radioquímico importante para el análisis de analitos no radiactivos es la dilución isotópica. Una fuente externa de analito se prepara en una forma radiactiva con una actividad conocida, A T, por su descomposición radiactiva, la llamamos trazador a esta forma del analito. Para preparar una muestra para su análisis agregamos una masa conocida del trazador, w T, a una porción de muestra que contiene una masa desconocida, w x, de analito. Después de homogeneizar la muestra y el trazador, aislamos w A gramos de analito mediante una serie de tratamientos químicos y físicos apropiados. Debido a que estos tratamientos químicos y físicos no pueden distinguir entre las formas radiactivas y no radiactivas del analito, el material aislado contiene ambas. Finalmente, se mide la actividad de la muestra aislada, A A. Si recuperamos todo el analito —tanto el trazador radiactivo como el analito no radiactivo— entonces A A y A T son iguales y w x = w A — w T. Normalmente, fallamos en recuperar todo el analito. En este caso, A A es menor que A T, y
\[A_{A}=A_{T} \times \frac{w_{A}}{w_{x}+w_{T}} \label{13.8}\]
La relación de pesos en la Ecuación\ ref {13.8} explica cualquier pérdida de actividad que resulte de nuestra incapacidad para recuperar todo el analito. Resolviendo la ecuación\ ref {13.8} para w x da
\[w_{x}=\frac{A_{T}}{A_{A}} w_{A}-w_{T} \label{13.9}\]
La forma en que procesamos la muestra depende del analito y de la matriz de la muestra. Podríamos, por ejemplo, digerir la muestra para poner el analito en solución. Después de filtrar la muestra para eliminar los sólidos residuales, podríamos precipitar el analito, aislarlo por filtración, secarlo en un horno y obtener su peso.
Dado que el objetivo de un análisis es determinar la cantidad de analito no radiactivo en nuestra muestra, el darse cuenta de que tal vez no recuperemos todo el analito podría parecerle inquietante. Recordemos del Capítulo 7.7, que una sola extracción líquido-líquido rara vez tiene una eficiencia de extracción del 100%. Una ventaja de la dilución de isótopos es que la eficiencia de extracción para el analito no radiactivo y para el trazador son las mismas. Si recuperamos el 50% del trazador, entonces también recuperamos el 50% del analito no radiactivo. Debido a que sabemos cuánto trazador agregamos a la muestra, podemos determinar qué cantidad del analito no radiactivo está en la muestra.
La concentración de insulina en una cuba de producción se determina por dilución isotópica. Se agrega una muestra de 1.00-mg de insulina marcada con 14 C que tiene una actividad de 549 cpm a una muestra de 10.0 mL tomada de la cuba de producción. Después de homogeneizar la muestra, una porción de la insulina se separa y purifica, produciendo 18.3 mg de insulina pura. La actividad para la insulina aislada se mide a 148 cpm. ¿Cuántos mg de insulina hay en la muestra original?
Solución
Sustituir valores conocidos en la ecuación\ ref {13.8} da
\[w_{x}=\frac{549 \text{ cpm}}{148 \text{ cpm}} \times 18.3 \text{ mg}-1.00 \text{ mg}=66.9 \text{ mg} \text { insulin } \nonumber\]
La ecuación\ ref {13.8} y la ecuación\ ref {13.9} son válidas solo si la vida media del trazador es considerablemente más larga que el tiempo que lleva realizar el análisis. Si no es así, entonces la disminución de la actividad se debe tanto a la recuperación incompleta como a la disminución natural de la actividad del trazador. El cuadro 13.3.1 proporciona una lista de varios trazadores comunes para la dilución de isótopos.
| isótopo | vida media |
|---|---|
| 3 H | 12.5 años |
| 14 C | 5730 años |
| 32 P | 14.3 días |
| 35 S | 87.1 días |
| 45 Ca | 152 días |
| 55 Fe | 2.91 años |
| 60 Co | 5.3 años |
| 131 I | 8 días |
Una característica importante de la dilución de isótopos es que no es necesario recuperar todo el analito para determinar la cantidad de analito presente en la muestra original. La dilución de isótopos, por lo tanto, es útil para el análisis de muestras con matrices complejas, donde una recuperación completa del analito es difícil.
Aplicaciones de Caracterización
Un ejemplo de aplicación de caracterización es la determinación de la edad de una muestra basada en la desintegración de un isótopo radiactivo presente de forma natural en la muestra. El ejemplo más común es la datación por carbono-14, que se utiliza para determinar la edad de los materiales orgánicos naturales.
A medida que los rayos cósmicos pasan por la atmósfera superior, algunos\(_7^{14}\text{N}\) átomos en la atmósfera capturan neutrones de alta energía, convirtiéndolos en\(_6^{14}\text{C}\). El\(_6^{14}\text{C}\) entonces migra a la atmósfera inferior donde se oxida para formar CO 2 marcado con C-14. Los animales y las plantas posteriormente incorporan este CO 2 marcado en sus tejidos. Debido a que este es un proceso en estado estacionario, todas las plantas y animales tienen la misma proporción de\(_6^{14}\text{C}\) a\(_6^{12}\text{C}\) en sus tejidos. Cuando un organismo muere, la desintegración radiactiva de\(_6^{14}\text{C}\) a\(_7^{14}\text{N}\) por\(_{-1}^0 \beta\) emisión (t = 5730 años) conduce a una reducción predecible en la\(_6^{12}\text{C}\) relación\(_6^{14}\text{C}\) a. Podemos usar el cambio en esta relación a muestras de fecha que tienen hasta 30000 años de antigüedad, aunque la precisión del análisis es mejor cuando la edad de la muestra es menor a 7000 años. La precisión de la datación por carbono-14 depende de nuestra suposición de que la\(_6^{12}\text{C}\) relación natural\(_6^{14}\text{C}\) a la atmósfera es constante a lo largo del tiempo. Alguna variación en la relación se ha producido como resultado del aumento del consumo de combustibles fósiles y la producción de\(_6^{14}\text{C}\) durante las pruebas de armas nucleares. Una curva de calibración preparada con muestras de edad conocida (ejemplos de muestras incluyen anillos de árboles, sedimentos oceánicos profundos, muestras de coral y depósitos en cuevas) limita esta fuente de incertidumbre.
No es necesario preparar una curva de calibración para cada análisis. En cambio, existe una curva de calibración universal conocida como IntCal. La curva más reciente de este tipo, IntCal13 se describe en el siguiente trabajo: Reimer, P. J., et. al. “IntCal13 y Marine 13 Curva de Calibración de Edad de Radiocarbono 0—50,000 Años Cal BP”, Radiocarbono 2013, 55, 1869—1887. Esta calibración abarca 50 000 años antes del presente (PA).
Para determinar la edad de una muestra de tejido,\(_6^{12}\text{C}\) se midió la relación relativa de\(_6^{14}\text{C}\) a arrojando un resultado de 80.9% del encontrado en las fibras modernas. ¿Qué edad tiene la tela?
Solución
La ecuación\ ref {13.3} y la ecuación\ ref {13.4} nos proporcionan un método para convertir un cambio en la relación de\(_6^{14}\text{C}\) a\(_6^{12}\text{C}\) a la edad de la tela. Dejando que A 0 sea la relación de\(_6^{14}\text{C}\) a\(_6^{12}\text{C}\) en fibras modernas, le asignamos un valor de 1.00. La relación de\(_6^{14}\text{C}\) a\(_6^{12}\text{C}\) en la muestra, A, es 0.809. Resolver da
\[t=\ln \frac{A_{0}}{A} \times \frac{t_{1 / 2}}{0.693}=\ln \frac{1.00}{0.809} \times \frac{5730 \text { yr }}{0.693}=1750 \text { yr } \nonumber\]
Se pueden utilizar otros isótopos para determinar la edad de una muestra. La edad de las rocas, por ejemplo, se ha determinado a partir de la relación entre el número de\(_{92}^{238}\text{U}\) y el número de\(_{82}^{206}\text{Pb}\) átomos estables producidos por la desintegración radiactiva. Para rocas que no contienen uranio, la datación se logra comparando la proporción de radiactivo\(_{19}^{40}\text{K}\) con respecto al estable\(_{18}^{40}\text{Ar}\). Otro ejemplo es la datación de sedimentos recolectados de lagos midiendo la cantidad de los\(_{82}^{210}\text{Pb}\) que está presente.
Evaluación
Los métodos radioquímicos se utilizan rutinariamente para el análisis de analitos traza en muestras macro y meso. La precisión y precisión de los métodos radioquímicos generalmente están dentro del rango del 1— 5%. Podemos mejorar la precisión, que está limitada por la naturaleza aleatoria de la descomposición radiactiva, contando la emisión de partículas radiactivas durante el tiempo que sea práctico. Si el número de recuentos, M, es razonablemente grande (M ≥ 100), y el período de conteo es significativamente menor que la vida media del isótopo, entonces el porcentaje de desviación estándar relativa para la actividad,\((\sigma_A)_{rel}\), es aproximadamente
\[\left(\sigma_{A}\right)_{\mathrm{rel}}=\frac{1}{\sqrt{M}} \times 100 \nonumber\]
Por ejemplo, si determinamos la actividad contando 10 000 partículas radiactivas, entonces la desviación estándar relativa es de 1%. La sensibilidad de un método radioquímico es inversamente proporcional a\((\sigma_A)_{rel}\), lo que significa que podemos mejorar la sensibilidad contando más partículas.
La selectividad rara vez es motivo de preocupación cuando se utiliza un método radioquímico porque la mayoría de las muestras tienen un solo isótopo radiactivo. Cuando hay varios isótopos radiactivos, podemos determinar la actividad de cada isótopo aprovechando las diferencias en las energías de sus respectivas partículas radiactivas o diferencias en sus respectivas tasas de desintegración.
En comparación con la mayoría de las otras técnicas analíticas, los métodos radioquímicos suelen ser más caros y requieren más tiempo para completar un análisis. Los métodos radioquímicos también están sujetos a importantes preocupaciones de seguridad debido a la posible exposición del analista a la radiación de alta energía y la necesidad de eliminar de manera segura los desechos radiactivos.