2.7: Gases reales
- Page ID
- 72360
Si bien la ley de gas ideal es suficiente para la predicción de un gran número de propiedades y comportamientos para los gases, hay una serie de veces que las desviaciones de la idealidad son extremadamente importantes.
La ecuación de van der Waals
Se han sugerido varias ecuaciones de estado para dar cuenta de las desviaciones de la idealidad. Una expresión simple, pero útil, es la propuesta por Johannes Diderik van der Waals (1837 — 1923) (Johannes Diderik van der Waals - Biográfico, 2014)
La ecuación de van der Waals introdujo correcciones a los términos de presión y volumen de la ley de gas ideal para dar cuenta de las interacciones intermoleculares y el tamaño molecular respectivamente.
\[ \left ( p + \dfrac{a}{V_m^2} \right) (V_m - b) = RT \label{vdw}\]
o
\[ p =\dfrac{RT}{V_m-b} - \dfrac{a}{V_m^2} \label{vdw2}\]
En esta expresión,\(a\) y\(b\) son variables de una sustancia dada las cuales se pueden medir y tabular. En general, las moléculas con grandes fuerzas intermoleculares tendrán grandes valores de\(a\), y las moléculas grandes tendrán grandes valores de b. Algunas constantes de van der Waals se dan en la Tabla\(\PageIndex{1}\).
| Frecuencia de colisiones de gas | a (atm L 2 mol-2) | b (L/mol) |
|---|---|---|
| Él | 0.0341 | 0.0238 |
| N 2 | 1.352 | 0.0387 |
| CO 2 | 3.610 | 0.0429 |
| C 2 H 4 | 4.552 | 0.0305 |
El modelo van der Walls es útil porque hace que sea muy sencillo interpretar los parámetros en términos de tamaño molecular y fuerzas intermoleculares. Pero también tiene limitaciones (¡como es el caso de todo modelo científico!) Algunas otras ecuaciones de estado útiles de dos parámetros y tres parámetros (o más) incluyen los modelos Redlich-Kwong, Dieterici y Clausius (Tabla\(\PageIndex{2}\)). Estos tienen la ventaja de que permiten la dependencia de la temperatura de algunos de los parámetros, que como se verá más adelante, es necesario modelar ciertos comportamientos de los gases reales.
| Modelo | Ecuación de Estado |
|---|---|
| Ideal | \(p = \dfrac{RT}{V_m}\) |
| van der Waals (van der Waals J. D., 1967) | \( p =\dfrac{RT}{V_m-b} - \dfrac{a}{V_m^2}\) |
| Redlich-Kwong (Redlich y Kwong, 1949) | \( p =\dfrac{RT}{V_m-b} - \dfrac{a}{\sqrt{T} V_m (V_m +b)}\) |
| Dieterici (Dieterici, 1899) | \( p =\dfrac{RT}{V_m-b} \exp \left( \dfrac{-a}{V_mRT} \right)\) |
| Clausius | \( p =\dfrac{RT}{V_m-b} - \dfrac{a}{T (V_m + c)^2}\) |
| Ecuaciones Virial | \( p =\dfrac{RT}{V_m} \left(1+ \dfrac{B(T)}{V_m} +\dfrac{C(T)}{V_m} \dots \right) \) |
La Ecuación Virial
Una expresión muy útil que permite desviaciones del comportamiento ideal es la Ecuación Virial de estado. Esta es una expansión simple de la serie de potencia en la que los términos de orden superior contienen todas las desviaciones de la ley de gas ideal.
\[ p =\dfrac{RT}{V_m} \left(1+ \dfrac{B(T)}{V_m} +\dfrac{C(T)}{V_m} \dots \right ) \label{viral}\]
En el límite de que B (T) (el Segundo Coeficiente Virial) y C (T) son cero, la ecuación se convierte en la ley de gas ideal. Además, el volumen molar de gases es pequeño, las contribuciones de los términos tercero, cuarto, etc. disminuyen en magnitud, permitiendo truncar la serie en un punto conveniente. El segundo coeficiente virial puede predecirse a partir de una función teórica de potencial intermolecular mediante
\[B(T) = N_a \int _{r=0}^{\infty} \left[ 1- \exp \left(\dfrac{U(r)}{k_BT} \right) \right] 2\pi r^2 \,dr\]
La calidad de un potencial intermolecular puede ser determinada (parcialmente) por la capacidad del potencial para predecir el valor del segundo coeficiente virial,\(B(T)\).
El potencial de Leonard-Jones
Se utiliza una función de potencial intermolecular para describir las interacciones entre moléculas. Estas interacciones tendrán que incluir fuerzas atractivas, que unirán a las moléculas, y fuerzas repulsivas que las separarán. Si las moléculas son esferas duras, carentes de interacciones atractivas, la función potencial es bastante simple.
\[ U(r) ={\begin{cases} \infty &{\text{for }}r\leq \sigma\\0&{\text{for }}r>\sigma.\end{cases}}\]
En esta función,\(\sigma\) está determinada por el tamaño de las moléculas. Si dos moléculas se encuentran a una distancia\(r\) la una de la otra, chocan, rebotando en una colisión perfectamente elástica. Las moléculas reales, sin embargo, tienen un rango de separaciones intermoleculares a través de las cuales experimentarán fuerzas atractivas (la llamada “pared blanda” de la superficie potencial). Y luego en separaciones muy pequeñas, dominarán las fuerzas repulsivas, separando las moléculas (la llamada “pared dura” de la superficie potencial).
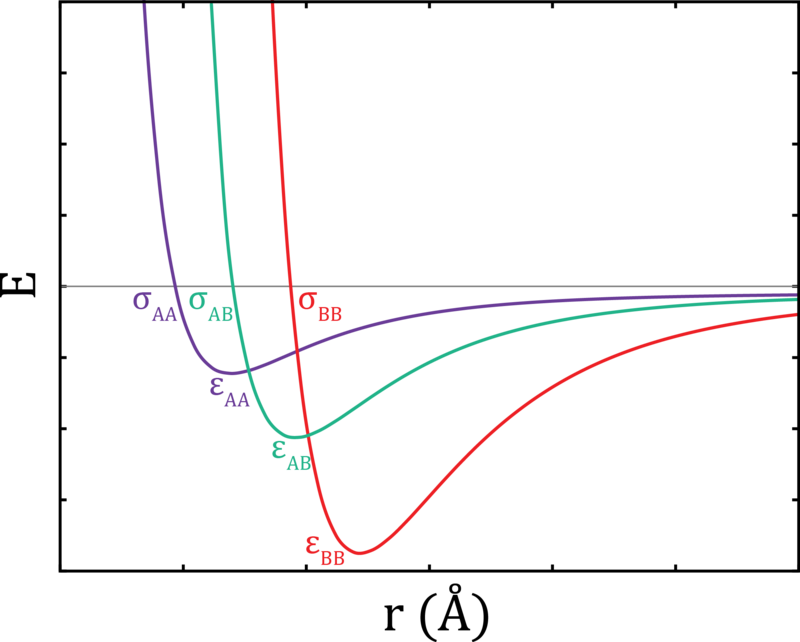
Un potencial intermolecular comúnmente utilizado,\(U(r)\), es el potencial Leonard-Jones. Esta función tiene la forma
\[ U(r) = 4 \epsilon \left[ \underbrace{\left(\dfrac{\sigma}{r}\right)^{12}}_{\text{repulsive term}} - \underbrace{\left(\dfrac{\sigma}{r}\right)^{6}}_{\text{attractive term}} \right] \]
donde\(\sigma\) gobierna el ancho del pozo potencial, y\(\epsilon\) gobierna la profundidad. La distancia entre moléculas viene dada por\(r\). Las interacciones repulsivas entre moléculas están contenidas en los primeros términos y las interacciones atractivas se encuentran en el segundo término.
Expansión de la serie Taylor
Un método comúnmente utilizado para crear una serie de potencias basada en otra ecuación es la Expansión de la Serie Taylor. Se trata de una expansión de una función sobre un punto de referencia útil donde cada uno de los términos se genera diferenciando la función original.
Para una función\(f(x)\), la serie Taylor se\(F(x)\) puede generar a partir de la expresión
\[F(x) = f(a) + \left.\dfrac{d}{dx} f(x) \right|_{x=a} (x-a) + \dfrac{1}{2!} \left. \dfrac{d^2}{dx^2} f(x) \right|_{x=a} (x-a)^2 + \dots\]
Esto se puede aplicar a cualquier ecuación de estado para derivar una expresión para los coeficientes viriales en términos de los parámetros de la ecuación de estado.
Aplicación a la ecuación de van der Waals
La ecuación de van der Waals se puede escribir en términos de volumen molar (Ecuación\ ref {vdw2}). Al multiplicar el lado derecho por\(\frac{u}{u}\) (donde\(u = 1/v\)) rinde:
\[ p =\dfrac{RTu}{1-bu} - au^2\]
Esta expresión puede ser “Talyor” expandida (a los tres primeros términos) sobre\(u = 0\) (lo que corresponde a un volumen molar infinito). Los términos de coeficiente que se necesitan para la expansión son
\[p(u=0)=0\]
\[ \dfrac{dp}{du} \big|_{u=0} = \left [ \dfrac{RT}{1-bu} + \dfrac{bRTu}{(1-bu)^2} - 2au \right]_{u=0} = RT\]
\[ \dfrac{d^2p}{du^2} \big|_{u=0} = \dfrac{1}{2} \left [ \dfrac{bRT}{(1-bu)^2} + \dfrac{bRT}{(1-bu)^2} - \dfrac{2b^2RTu}{(1-bu)^3} - 2au \right]_{u=0} = RT -a\]
\[ \dfrac{d^3p}{du^3} \big|_{u=0} = RTb^2\]
Y la ecuación virial puede entonces expresarse en términos de los parámetros de van der Waals como
\[ p = 0 +RT(u) + (bRT -a)(u)^2 + RTb^{2(u)^3}\]
Sustituir\(u = 1/V\) y simplificar da el resultado deseado:
\[ p= RT \left[ \dfrac{1}{V} + \dfrac{b-\frac{a}{RT}}{V^2} + \dfrac{b^2}{V^3} + \dots \right]\]
Y el segundo coeficiente virial viene dado por
\[ B(T) = b-\dfrac{a}{RT}\]
La temperatura de Boyle
Una manera útil en la que se pueden expresar las desviaciones de la idealidad es definiendo el factor de compresión (\(Z\)) dado por
\[ Z = \dfrac{pV_m}{RT}\]
donde\(V_m\) está el volumen molar. Para un gas ideal,\(Z = 1\) bajo todas las combinaciones de\(P\),\(V_m\), y\(T\). Sin embargo, los gases reales mostrarán alguna desviación (aunque todos los gases se acercan al comportamiento ideal a p baja, V m alta y T alta) El factor de compresión para nitrógeno a varias temperaturas se muestra a continuación en un rango de presiones.
Como se puede ver, el gas se comporta más cerca de lo ideal en un rango de presión más largo a las temperaturas más altas. En general, hay una temperatura, la temperatura de Boyle, a la que un gas se aproximará al comportamiento ideal ya que la presión va a cero asintóticamente, y así comportarse idealmente sobre un amplio rango de presiones más bajas. La temperatura de Boyle se encuentra resolviendo
\[ \lim_{p \rightarrow 0} \left( \dfrac{\partial Z}{\partial p} \right) = 0\]
o
\[ \lim_{1/V_m \rightarrow 0} \left( \dfrac{\partial Z}{\partial \left(\frac{1}{V_m} \right)} \right) = 0\]
Usando la ecuación virial de estado (Ecuación\ ref {viral}), la temperatura de Boyle se puede expresar en términos de los coeficientes viriales. Comenzando con el factor de compresión
\[Z = 1 +\dfrac{B}{V_m} + \dots\]
y luego diferenciar con respecto a los\(1/V_m\) rendimientos
\[\dfrac{\partial Z}{\partial \left(\frac{1}{V_m}\right)} = B\]
Por lo que se puede concluir que a la temperatura de Boyle, el segundo coeficiente virial\(B\) es igual a cero. Esto debería tener cierto sentido dado que el primer coeficiente virial proporciona la mayor parte de la desviación de la ley del gas ideal, por lo que debe desvanecerse a medida que el gas se comporta de manera más ideal.
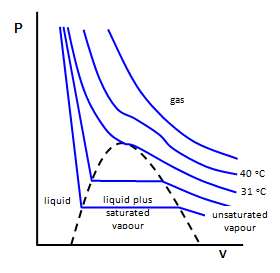
Comportamiento Crítico
Las isotermas (líneas de temperatura constante) del CO 2 revelan una desviación muy grande del comportamiento ideal. A altas temperaturas, el CO 2 se comporta de acuerdo con la Ley de Boyle. Sin embargo, a temperaturas más bajas, el gas comienza a condensarse para formar un líquido a altas presiones. A una temperatura específica, la temperatura crítica, la isoterma comienza a mostrar este comportamiento crítico. La temperatura, presión y volumen molar (\(p_c\)\(T_c\), y\(V_c\)) en este punto definen el punto crítico. Para resolver expresiones para las constantes críticas, se requieren tres ecuaciones. La ecuación de estado proporciona una relación. El segundo se puede generar reconociendo que la pendiente de la isoterma en el punto crítico es cero. Y finalmente, la tercera expresión se deriva al reconocer que la isoterma pasa por un punto de inflexión en el punto crítico. Usando la ecuación de van der Waals como ejemplo, estas tres ecuaciones se pueden generar de la siguiente manera:
Resolver estas expresiones para\(p_c\)\(T_c\), y\(V_c\) rendimientos
\[p_c = \dfrac{a}{27b^2}\]
\[T_c = \dfrac{8a}{27bR}\]
\[V_c = 3b\]
Las variables críticas pueden ser utilizadas de esta manera para determinar los valores de los parámetros moleculares utilizados en una ecuación de estado (como la ecuación de van der Waals) para una sustancia dada.
El Principio de los Estados Correspondientes
El principio de estados correspondientes fue propuesto por van der Waals en 1913 (van der Waals J. D., 1913). Señaló que el factor de compresión en el punto crítico
\[Z_c = \dfrac{p_cV_c}{RT_c}\]
es casi lo mismo para cualquier sustancia. Esto es consistente con lo que predice la ecuación de van der Waals, que predice\(Z_c = 0.375\) independientemente de la sustancia.
Además, se puede observar que a partir de variables reducidas definidas por
\[p_r= \dfrac{p}{p_c}\]
\[V_r= \dfrac{V}{V_c}\]
\[T_r= \dfrac{T}{T_c}\]
se encuentra que varias propiedades físicas son comparables para sustancias reales. Por ejemplo (Guggenheim, 1945), para argón, criptón, nitrógeno, oxígeno, dióxido de carbono y metano la compresibilidad reducida es
\[[ \dfrac{p_cV_c}{RT_c} \approx 0.292\]
Además, el factor de compresión reducido puede representarse como una función de la presión reducida para varias sustancias en varias isotermas reducidas con consistencia sorprendente independientemente de la sustancia: