14.4: Termoquímica y Calorimetría
- Page ID
- 70612
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Asegúrese de comprender a fondo los siguientes conceptos esenciales:
- Escriba una ecuación termoquímica equilibrada que exprese el cambio de entalpía para una reacción química dada. Asegúrese de especificar correctamente el estado físico (y, si es necesario, la concentración) de cada componente.
- Escribir una ecuación que defina la entalpía estándar de formación de una especie química dada.
- Definir el cambio de entalpía estándar de una reacción química. Utilice una tabla de entalpías estándar de formación para evaluar ΔH f°.
- Declarar el principio del que depende la ley de Hess, y explicar por qué esta ley es tan útil.
- Describir un calorímetro simple y explicar cómo se emplea y cómo se determina su capacidad calorífica.
El calor que fluye a través de los límites de un sistema que experimenta un cambio es una propiedad fundamental que caracteriza el proceso. Se mide fácilmente, y si el proceso es una reacción química realizada a presión constante, también se puede predecir a partir de la diferencia entre las entalpías de los productos y los reactivos. El estudio cuantitativo y la medición de los cambios de calor y entalpía se conoce como termoquímica.
Ecuaciones termoquímicas y estados estándar
Para definir las propiedades termoquímicas de un proceso, primero es necesario escribir una ecuación termoquímica que defina el cambio real que se está produciendo, tanto en términos de las fórmulas de las sustancias involucradas como de sus estados físicos (temperatura, presión, y ya sea sólido, líquido, o gaseosas.
Por tomar un ejemplo muy simple, aquí está la ecuación termoquímica completa para la vaporización del agua en su punto de ebullición normal:
\[\ce{H2O(\ell,\, 373 \,K, \,1 \,atm) → H2O(g, \,373 \,K, \,1 \,atm)} \,\,\,ΔH = 40.7\, kJ\, mol^{-1}\]
La cantidad 40.7 se conoce como la entalpía de vaporización (a menudo denominada “calor de vaporización”) del agua líquida. Se deben tener en cuenta los siguientes puntos al escribir ecuaciones termoquímicas:
Cualquier cantidad termodinámica como la\(ΔH\) que se asocia a una ecuación termoquímica siempre se refiere al número de moles de sustancias que se muestran explícitamente en la ecuación. Así para la síntesis del agua podemos escribir
\[\ce{2 H2(g) + O2(g)→ 2 H2O(l) }\,\,\,ΔH = -572 \,kJ\]
o
\[\ce{H2(g) + 1/2 O2(g)→ H2O(l)} \,\,\, ΔH = -286 \,kJ\]
Las ecuaciones termoquímicas para las reacciones que tienen lugar en solución también deben especificar las concentraciones de las especies disueltas. Por ejemplo, la entalpía de neutralización de un ácido fuerte por una base fuerte viene dada por
\[\ce{H^{+}(aq,\, 1M,\, 298\, K,\, 1\, atm) + OH^{-} (aq,\, 1M,\, 298 \,K,\, 1 \,atm) → H2O(\ell, 373\, K,\, 1 \,atm) } \,\,\, ΔH = -56.9\, kJ\, mol^{-1}\]
en el que la abreviatura aq se refiere a los iones hidratados tal como existen en solución acuosa. Dado que la mayoría de las ecuaciones termoquímicas están escritas para las condiciones estándar de 298 K y 1 atm de presión, podemos dejar estas cantidades fuera si estas condiciones se aplican tanto antes como después de la reacción. Si, bajo estas mismas condiciones, la sustancia se encuentra en su estado físico preferido (más estable), entonces se dice que la sustancia está en su estado estándar.
Así, el estado estándar del agua a 1 atm es el sólido por debajo de 0°C, y el gas por encima de 100°C.Una cantidad termoquímica como la\(ΔH\) que se refiere a reactivos y productos en sus estados estándar se denota por\(ΔH^°\).
Concentraciones vs. concentraciones efectivas (actividades)
En el caso de las sustancias disueltas, el estado estándar de un soluto es aquel en el que la “concentración efectiva”, conocida como la actividad, es la unidad. Para los solutos no iónicos la actividad y molaridad suelen ser aproximadamente las mismas para concentraciones de hasta aproximadamente 1M, pero para un soluto iónico esta aproximación es generalmente válida solo para soluciones más diluidas que 0.001-0.01M, dependiendo de la carga eléctrica y tamaño del ion particular.
Entalpía Estándar de Formación
El cambio de entalpía para una reacción química es la diferencia
\[ΔH = H_{products} - H_{reactants}\]
Si la reacción en cuestión representa la formación de un mol del compuesto a partir de sus elementos en sus estados estándar, como en
\[\ce{H2(g) + 1/2O2(g) -> H2O(l)} \;\;\; ΔH = -286\; kJ\]
entonces podemos establecer arbitrariamente la entalpía de los elementos a cero y escribir
\[\begin{align*} H_f^o &= \sum H_f^o (products) - \sum H_f^o (reactants) \\[4pt] &= -286\; kJ - 0 \\[4pt] &= -268\; kJ \,mol^{-1} \end{align*}\]
que define la entalpía estándar de formación de agua a 298 K. El valor H f° = -268 kJ nos dice que cuando hidrógeno y oxígeno, cada uno a una presión de 1 atm y a 298 K (25° C) reaccionan para formar 1 mol de agua líquida también a 25°C y 1 atm de presión, 268 kJ tendrán pasó del sistema (la mezcla de reacción) a los alrededores. El signo negativo indica que la reacción es exotérmica: la entalpía del producto es menor que la de los reactivos. La entalpía estándar de formación es una propiedad fundamental de cualquier compuesto. El Cuadro T1 enumera los valores de H f° (generalmente junto a valores de otras propiedades termodinámicas) en sus apéndices.
La entalpía estándar de formación de un compuesto se define como el calor asociado a la formación de un mol del compuesto a partir de sus elementos en sus estados estándar.
En general, el cambio de entalpía estándar para una reacción viene dado por la expresión
\[ΔH_f^o= \sum H_f^o (products) - \sum H_f^o (reactants) \label{2-1}\]
en el que los\(\sum H_f^o\) términos indican las sumas de las entalpías estándar de formaciones de todos los productos y reactivos. La definición anterior es una de las más importantes en química porque nos permite predecir el cambio de entalpía de cualquier reacción sin saber más que las entalpías estándar de formación de los productos y reactivos, las cuales están ampliamente disponibles en tablas.
Los siguientes ejemplos ilustran algunos aspectos importantes de la entalpía estándar de formación de sustancias.
La ecuación termoquímica que define siempre\(H_f^o\) se escribe en términos de un mol de la sustancia en cuestión> Por ejemplo, la ecuación termodinámica relavante para el calor de formación de amoníaco (\(\ce{NH3}\)) es:
\[\ce{ 1/2 N2(g) + 3/2 H2(g)→ NH3(g)}\,\,\, ΔH^o = -46.1\, kJ \,(\text{per mole of } \ce{NH3}) \nonumber\]
El calor estándar de formación de un compuesto siempre se toma en referencia a las formas de los elementos que son más estables a 25°C y 1 atm de presión.
Varios elementos, de los cuales el azufre y el carbono son ejemplos comunes, pueden existir en más de una forma cristalina sólida (llamada alótropos). Para el dixoide\(ce{CO2}\) de carbono (se pueden construir dos ecuaciones termodinámicas:
\[\ce{C(graphite) + O2(g) → CO2(g)}\,\,\, ΔH^o ≡ H_f^o = -393.5\, kJ\, mol^{-1} \nonumber\]
\[\ce{C(diamond) + O2(g) → CO2(g)}\,\,\, ΔH^{o} = -395.8\, kJ\, mol^{-1} \nonumber\]
Sin embargo, para el carbono, la forma de grafito es la forma más estable y las ecuaciones termodinámicas correctas para el calor de formación.
El estado físico del producto de la reacción de formación debe indicarse explícitamente si no es el más estable a 25°C y 1 atm de presión:
\[\ce{H2(g) + 1/2 O2(g) → H2O(aq)}\,\,\, ΔH^o ≡ H_f^o = -285.8\, kJ\, mol^{-1} \nonumber\]
\[\ce{H2(g) + 1/2 O2(g) → H2O(g)} \,\,\, ΔH^o = -241.8\, kJ\, mol^{-1} \nonumber\]
Observe que la diferencia entre estos dos\(ΔH^o\) valores es solo el calor de vaporización del agua.
Aunque la formación de la mayoría de las moléculas a partir de sus elementos es un proceso exotérmico, la formación de algunos compuestos es ligeramente endotérmica:
\[\ce{1/2 N2(g) + O2(g) -> NO2(g)}\,\,\, ΔH^o ≡ H_f^° = +33.2\, kJ\, mol^{-1} \nonumber\]
Un calor positivo de formación se asocia frecuentemente con inestabilidad, la tendencia de una molécula a descomponerse en sus elementos, aunque no es en sí misma una causa suficiente. En muchos casos, sin embargo, la tasa de esta descomposición es esencialmente cero, por lo que aún es posible que la sustancia exista. En este sentido, vale la pena señalar que todas las moléculas se volverán inestables a temperaturas más altas.
Las reacciones termoquímicas que definen los calores de formación de la mayoría de los compuestos no pueden tener lugar realmente. Por ejemplo, la síntesis directa de metano a partir de sus elementos
\[\ce{C(graphite) + 2 H2(g) → CH4(g)} \nonumber\]
no pueden observarse directamente debido al gran número de otras posibles reacciones entre estos dos elementos. Sin embargo, el cambio estándar de entalpía para tal reacción se encuentra indirectamente a partir de otros datos, como se explica en la siguiente sección.
La entalpía estándar de formación de átomos gaseosos a partir del elemento se conoce como el calor de atomización.
Los calores de atomización son siempre positivos, y son importantes en el cálculo de las energías de enlace.
\[\ce{Fe(s) → Fe(g)}\,\, ΔH° = 417 \,kJ\, mol^{-1} \nonumber\]
La entalpía estándar de formación de un ion disuelto en agua se expresa en una escala separada en la que la de\(\ce{H^{+}(aq)}\) se define como cero.
El calor estándar de formación de un ion disuelto tal como\(\ce{Cl^{-}(aq)}\) (es decir, la formación del ion a partir del elemento) no se puede medir porque es imposible tener una solución que contenga un solo tipo de ion. Por esta razón, las entalpías iónicas se expresan en una escala separada en la que\(\ce{H_f^o}\) del ión hidrógeno a la actividad unitaria (concentración efectiva 1 M) se define como cero:
\[\ce{1/2 H2(g) → H^{+}(aq)}\,\,\, ΔH^o ≡ H_f^o = 0\, kJ\, mol^{-1} \nonumber\]
Otras entalpías iónicas (como se las conoce comúnmente) se encuentran combinando ecuaciones termoquímicas apropiadas (como se explica en la Sección 3 a continuación). Por ejemplo, H f° de HCl (ac) se encuentra a partir de las entalpías de formación y solución de HCl (g), produciendo
\[\ce{1/2 H2(g) + 1/2 Cl2(g) → HCl(aq)}\,\,\,\ ΔH^o ≡ H_f^o = -167\, kJ\, mol^{-1} \nonumber\]
Debido a que H f° para H + (aq) es cero, este valor establece la entalpía estándar del ion cloruro. La entalpía estándar de formación de Ca 2+ (aq), dada por
\[\ce{Ca(s) + Cl2(g) -> CaCl2(aq)} \nonumber\]
podría entonces calcularse combinando otras cantidades medibles como las entalpías de formación y solución de\(\ce{CaCl2(s)}\) para encontrar H f° para CaCl 2 (aq), a partir de la cual H f° de\(\ce{Ca^{2+}(aq)}\) se encuentra por diferencia de la de \(\ce{Cl^{-}(aq)}\). Las tablas de las entalpías iónicas resultantes están ampliamente disponibles (ver aquí).
Ley de Hess y Cálculos Termoquímicos
Dos o más ecuaciones químicas se pueden combinar algebraicamente para dar una nueva ecuación. Incluso antes de que la ciencia de la termodinámica se desarrollara a finales del siglo XIX, se observó que los calores asociados a las reacciones químicas pueden combinarse de la misma manera para producir el calor de otra reacción. Por ejemplo, los cambios estándar de entalpía para la oxidación de grafito y diamante se pueden combinar para obtener ΔH° para la transformación entre estas dos formas de carbono sólido, reacción que no se puede estudiar experimentalmente.
\[\ce{C(graphite) + O2(g)→ CO2(g)}\,\,\, ΔH^o = -393.51\, kJ\, mol^{-1}\]
\[\ce{C(diamond) + O2(g)→ CO2(g)} \,\,\, ΔH^o = -395.40\, kJ\, mol^{-1}\]
La resta de la segunda reacción de la primera (es decir, escribir la segunda ecuación a la inversa y sumarla a la primera) rinde
\[\ce{C(graphite) → C(diamond)}\,\,\, ΔH^{°} = 1.89\, kJ\, mol^{-1}\]
Este principio, conocido como ley de Hess' de la suma de calor independiente, es una consecuencia directa de que la entalpía es una función de estado. La ley de Hess' es una de las herramientas más poderosas de la química, ya que permite predecir el cambio en la entalpía (y en otras funciones termodinámicas) de un gran número de reacciones químicas a partir de una base relativamente pequeña de datos experimentales.
Germain Henri Hess
Germain Henri Hess (1802-1850) fue un profesor de química nacido en Suiza en San Petersburgo, Rusia. Formuló su famosa ley, que descubrió empíricamente, en 1840. Parece que se sabe muy poco sobre su otra obra en química.
Entalpías Estándar de Combustión
Debido a que la mayoría de las sustancias no se pueden preparar directamente a partir de sus elementos, los calores de formación de compuestos rara vez se determinan por medición directa. En cambio, la ley de Hess se emplea para calcular entalpías de formación a partir de datos más accesibles. Las más importantes son las entalpías estándar de combustión. La mayoría de los elementos y compuestos se combinan con el oxígeno, y muchas de estas oxidaciones son altamente exotérmicas, lo que hace que la medición de sus calores sea relativamente fácil. Por ejemplo, combinando los calores de combustión de carbono, hidrógeno y metano, podemos obtener la entalpía estándar de formación de metano, que como señalamos anteriormente, no se puede determinar directamente (Ejemplo\(\PageIndex{1}\)).
Utilice la siguiente información de calor de formación/combustión para estimar el calor estándar de formación de metano\(\ce{CH4}\).
\[\begin{aligned} \ce{C(graphite)} + \ce{O2(g)} &→ \ce{CO2(g)} \quad &ΔH° = -393\, kJ\, mol^{-1} \label{P1-1} \\[4pt] \ce{H2(g)} + \ce{1/2 O2(g)} &→ \ce{H2O(g)} \quad &ΔH° = -286 kJ mol^{-1} \label{P1-2} \\[4pt] \ce{CH4(g)} + \ce{2O2(g)} &→ \ce{CO2(g)} + \ce{2H2O(g)} \quad &ΔH^o = -890\, kJ\, mol^{-1} \label{P1-3} \end{aligned}\]
Solución
El calor estándar de formación de metano se define por la reacción
\[\ce{C(graphite) + 2H2(g) → CH4(g)} \quad ΔH^o = ? \label{P1-4}\]
Nuestra tarea es así combinar las tres ecuaciones principales de tal manera que sumen hasta (4).
Paso 1
Comience por señalar que (3), la combustión de metano, es la única ecuación que contiene el término CH 4, por lo que necesitamos escribirlo a la inversa (¡sin olvidar revertir el signo de Δ H°!) para que CH 4 aparezca como producto.
\[\ce{CO2(g) + 2H2O(g) → CH4(g) + 2O2(g)} \quad ΔH^o = +890\, kJ\, mol^{-1} \label{P1-3Rev}\]
Paso 2
Dado que H 2 O no aparece en la reacción neta (4), agregue dos veces (2) para cancelar estas. Observe que esto también cancela uno de los oxígenos en (3Rev):
CO 2 (g) + 2H 2 O (g) → CH 4 (g) + 2 O 2 (g) Δ H° = +890 kJ mol -1 (P1-3Rev)
→ 2H 2 O (g) Δ H° = -484 kJ mol -1 (P1-2)
Paso 3
Por último, deshazte del O 2 y el CO 2 restantes agregando (1); esto también agrega una C necesaria:
→ CH 4 (g) + 2O 2 (g) Δ H° = +890 kJ mol -1 (P1-3Rev)→ 2H 2 O (g) Δ H° = -572 kJ mol -1 (P1-2)
→ CO 2 (g) Δ H° = -393 kJ mol -1 (P1-1)
Paso 4
Por lo que nuestra cancelación creativa ha eliminado todas excepto las sustancias que aparecen en (4). Solo sume los cambios de entalpía y terminamos:
\[\ce{C(graphite) + 2H2(g) → CH4(g)} \]
(El valor tabulado es -74.6 kJ mol -1)
Calorimetría: Medición de Δ H en el laboratorio
¿Cómo se determinan experimentalmente los cambios de entalpía? Primero, hay que entender que la única cantidad térmica que se puede observar directamente es el calor q que fluye dentro o fuera de un recipiente de reacción, y que q es numéricamente igual a Δ H° solo bajo la condición especial de presión constante. Además, q es igual al cambio de entalpía estándar solo cuando los reactivos y productos están ambos a la misma temperatura, normalmente 25°C.La medición de q se conoce generalmente como calorimetría.
Los tipos más comunes de calorímetros contienen una cantidad conocida de agua que absorbe el calor liberado por la reacción. Debido a que la capacidad calorífica específica del agua (4.184 J g -1 K -1) es conocida con alta precisión, una medición de su aumento de temperatura debido a la reacción permite calcular la cantidad de calor liberado.
En todos menos en los calorímetros muy simples, parte del calor liberado por la reacción es absorbido por los componentes del propio calorímetro. Por lo tanto, es necesario “calibrar” el calorímetro midiendo el cambio de temperatura que resulta de la introducción de una cantidad conocida de calor. La constante calorímetro resultante, expresada en J K -1, puede considerarse como la “capacidad calorífica del calorímetro”. La fuente de calor conocida generalmente se produce haciendo pasar una cantidad conocida de corriente eléctrica a través de una resistencia dentro del calorímetro, pero se puede medir por otros medios como se describe en el siguiente ejemplo problemático.
Al determinar la capacidad calorífica de un calorímetro, un estudiante mezcla 100.0 g de agua a 57.0 °C con 100.0 g de agua, ya en el calorímetro, a 24.2°C. (el calor específico del agua es 4.184 J g -1 K -1). Después de mezclar y equilibrar térmicamente con el calorímetro, la temperatura del agua se estabiliza a 38.7°C Calcular la capacidad calorífica del calorímetro en J/K.
Solución
El agua caliente pierde calor, el agua fría gana calor y el propio calorímetro gana calor, por lo que esto es esencialmente un problema de equilibrio térmico. La conservación de la energía requiere que
\[q_{hot} + q_{cold} + q_{cal} = 0 \nonumber\]
Podemos evaluar los dos primeros términos a partir de los cambios de temperatura observados:
\[q_{hot} = (100\; g) (38.7\;K - 57.0\;K) (4.184\; J \;g^{-1}K^{-1}) = -7,657\; J \nonumber\]
\[q_{cold} = (100\; g) (38.7 \;K - 24.2 \;K) (4.184\; J\; g^{-1} K^{-1}) = 6,067\; J \nonumber\]
Entonces
\[q_{cal} = 7,657 \;J - ,6067\; J = 1,590;\ J \nonumber\]
La constante del calorímetro es
\[\dfrac{1590\; J}{38.7\; K - 24.2\; K} = 110\; J\; K^{-1} \nonumber\]
Nota: Estrictamente hablando, existe un cuarto término de balance térmico que debe considerarse en un cálculo de alta precisión: el agua en el calorímetro se expande a medida que se calienta, realizando trabajos sobre la atmósfera.
Para las reacciones que se pueden iniciar combinando dos soluciones, el aumento de temperatura de la solución misma puede proporcionar un valor aproximado de la entalpía de reacción si asumimos que la capacidad calorífica de la solución es cercana a la del agua pura, lo que será casi cierto si las soluciones se diluyen.
Por ejemplo, una determinación calorimétrica muy simple de la entalpía estándar de la reacción
\[\ce{H^{+}(aq) + OH^{-}(aq) → H2O(\ell)} \nonumber\]
podría llevarse a cabo combinando volúmenes iguales de soluciones 0.1M de HCl y de NaOH inicialmente a 25°C. Dado que esta reacción es exotérmica, se liberará una cantidad de calor q en la solución. A partir del aumento de temperatura y del calor específico del agua, se obtiene el número de julios de calor liberados en cada gramo de la solución, y q después se puede calcular a partir de la masa de la solución. Dado que todo el proceso se lleva a cabo a presión constante, tenemos Δ H° = q.
Para reacciones que no pueden llevarse a cabo en solución acuosa diluida, el recipiente de reacción se coloca comúnmente dentro de un recipiente aislado de agua más grande. Durante la reacción, el calor pasa entre los recipientes interior y exterior hasta que sus temperaturas se vuelven idénticas. Nuevamente, se observa el cambio de temperatura del agua, pero en este caso necesitamos conocer el valor de la constante calorímetro descrita anteriormente.
El calorímetro de bombas
\(\Delta H_{combustion}\), ya que éstas son esenciales para la determinación de entalpías estándar de formación de los miles de nuevos compuestos que se preparan y caracterizan cada mes. En un calorímetro de volumen constante, el sistema está sellado o aislado de su entorno, y esto explica por qué su volumen es fijo y no se realiza ningún trabajo de volumen-presión. Una estructura de calorímetro de bomba consta de lo siguiente:- Bomba de acero que contiene los reactivos
- Baño de agua en el que se sumerge la bomba
- Termómetro
- Un agitador motorizado
- Alambre para ignición
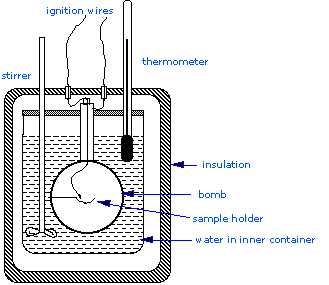
Dado que el proceso se lleva a cabo a volumen constante, el recipiente de reacción debe construirse para soportar la alta presión resultante del proceso de combustión, lo que equivale a una explosión confinada. El buque suele llamarse “bomba”, y la técnica se conoce como calorimetría de bomba. La reacción se inicia mediante la descarga de un condensador a través de un cable delgado que enciende la mezcla.
Otra consecuencia de la condición de volumen constante es que el calor liberado corresponde a q v, y así al cambio de energía interna Δ U en lugar de a Δ H. El cambio de entalpía se calcula de acuerdo con la fórmula
\[ΔH = q_v + Δn_gRT\]
- \(Δn_g\)es el cambio en el número de moles de gases en la reacción.
Se encendió una muestra de bifenilo (C 6 H 5) 2 que pesaba 0.526 g en un calorímetro de bomba inicialmente a 25°C, produciendo un aumento de temperatura de 1.91 K. En un experimento de calibración separado, se encendió una muestra de ácido benzoico C 6 H 5 COOH que pesaba 0.825 g bajo idénticas condiciones y produjo un aumento de temperatura de 1.94 K. Para el ácido benzoico, se sabe que el calor de combustión a presión constante es de 3226 kJ mol -1 (es decir, Δ U = -3226 kJ mol -1.) Utilice esta información para determinar la entalpía estándar de combustión de bifenilo.
Solución
Comience por elaborar la constante del calorímetro:
- Moles de ácido benzoico:
\[\dfrac{(0.825 g}{122.1 \;g/mol} = 0.00676\; mol\]
- Calor liberado al calorímetro:
\[(0.00676\; mol) \times (3226\; kJ/mol) = 21.80\; kJ\]
- Constante del calorímetro:
\[\dfrac{21.80\; kJ}{1.94\; K} = 11.24\; kJ/K\]
Ahora determinar\(ΔU_{combustion}\) del bifenilo (“BP”):
- moles de bifenilo:
\[\dfrac{0.526\; g}{154.12\; g/mol} = 0.00341 \; mol\]
- calor liberado al calorímetro:
\[(1.91\; K) \times (11.24\; kJ/K) = 21.46\; kJ\]
- calor liberado por mol de bifenilo:
\[\dfrac{21.46\; kJ}{0.00341\; mol} = 6,293\; kJ/mol\]
\[ΔU_{combustion} (BP) = -6,293\; kJ/mol\]
(Este es el cambio de calor a volumen constante\(q_v\); el signo negativo indica que la reacción es exotérmica, como lo son todas las reacciones de combustión).
De la ecuación de reacción
\[(C_6H_5)_{2(s)} + \frac{19}{2} O_{2(g)} \rightarrow 12 CO_{2(g)} + 5 H_2O_{(l)}\]
tenemos
\[Δn_g = 12 - \frac{19}{2} = \frac{-5}{2}\]
De esta manera, el volumen del sistema disminuye cuando tiene lugar la reacción. Convirtiendo a Δ H, podemos escribir la siguiente ecuación. Adicionalmente, recordemos que a volumen constante,\(ΔU = q_V\).
\[ΔH = q_V + Δn_gRT \]
\[ΔH = ΔU -\left( \dfrac{5}{2}\right) (8.314\; J\; mol^{-1}\; K^{-1}) (298 \;K)= \]
\[ ΔH=(-6,293 \; kJ/mol)-(6,194\; J/mol)=(-6,293-6.2)\;kJ/mol= -6299 \; kJ/mol\]
Un error común aquí es olvidar que el término restado está en J, no en kJ. Obsérvese que los 6.2 kJ adicionales en\(ΔH\) comparación con\(ΔU\) reflejan el trabajo que los alrededores realizan en el sistema a medida que el volumen de gases disminuye de acuerdo con la ecuación de reacción.
Determinar el calor de reacción
La cantidad de calor que el sistema cede a su entorno para que pueda regresar a su temperatura inicial es el calor de reacción. El calor de reacción es solo el negativo de la energía térmica ganada por el calorímetro y su contenido (\(q_{calorimeter}\)) a través de la reacción de combustión.
\[q_{rxn} = -q_{calorimeter} \label{2A}\]
donde
\[q_{calorimeter} = q_{bomb} + q_{water} \label{3A}\]
Si el calorímetro de volumen constante se configura de la misma manera que antes, (misma bomba de acero, misma cantidad de agua, etc.) entonces la capacidad calorífica del calorímetro se puede medir usando la siguiente fórmula:
\[q_{calorimeter} = \text{( heat capacity of calorimeter)} \times \Delta{T} \label{4A}\]
La capacidad calorífica se define como la cantidad de calor necesaria para aumentar la temperatura de todo el calorímetro en 1 °C. La ecuación anterior también se puede usar para calcular a\(q_{rxn}\) partir de\(q_{calorimeter}\) la ecuación 2. La capacidad calorífica del calorímetro se puede determinar mediante la realización de un experimento.
1.150 g de sacarosa pasan por combustión en un calorímetro de bomba. Si la temperatura subió de 23.42°C a 27.64°C y la capacidad calorífica del calorímetro es de 4.90 kJ/°C, entonces determinar el calor de combustión de la sacarosa,\(C_{12}H_{22}O_{11}\), en kJ por mol de\(C_{12}H_{22}O_{11}\).
Dado:
- masa de\(C_{12}H_{22}O_{11}\): 1.150 g
- \(T_{initial}\): 23.42°C
- \(T_{final}\):27.64°C
- Capacidad calorífica del calorímetro: 4.90 kJ/°C
Solución
Usando la Ecuación 4 para calcular\(q_{calorimeter}\):
\[q_{calorimeter} = (4.90\; kJ/°C) \times (27.64 - 23.42)°C = (4.90 \times 4.22) \;kJ = 20.7\; kJ \]
Conéctate a la Ecuación 2:
\(q_{rxn} = -q_{calorimeter} = -20.7 \; kJ \;\)
Pero la pregunta pregunta por KJ/mol\(C_{12}H_{22}O_{11}\), así que esto necesita ser convertido:
\(q_{rxn} = \dfrac{-20.7 \; kJ}{1.150 \; g \; C_{12}H_{22}O_{11}} = \dfrac{-18.0 \; kJ}{g\; C_{12}H_{22}O_{11}}\)
Por Mole\(C_{12}H_{22}O_{11}\):
\(q_{rxn} = \dfrac{-18.0 \; kJ}{g \; C_{12}H_{22}O_{11}} \times \dfrac{342.3 \; g \; C_{12}H_{22}O_{11}}{1 \; mol \; C_{12}H_{22}O_{11}} = \dfrac{-6.16 \times 10^3 \; kJ \;}{mol \; C_{12}H_{22}O_{11}}\)
Calorímetros
Si bien la calorimetría es simple en principio, su práctica es un arte altamente exigente, especialmente cuando se aplica a procesos que ocurren lentamente o implican cambios de calor muy pequeños, como la germinación de semillas. Los calorímetros pueden ser tan simples como una taza de café de espuma plástica, que a menudo se usa en laboratorios estudiantiles. Los calorímetros de grado de investigación, capaces de detectar pequeños cambios de temperatura, tienen más probabilidades de ocupar mesas o incluso habitaciones enteras:
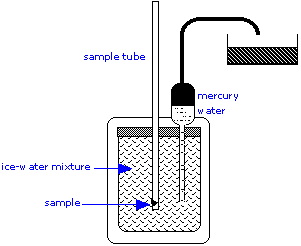
El calorímetro de hielo es una herramienta importante para medir las capacidades caloríficas de líquidos y sólidos, así como los calores de ciertas reacciones. Este sencillo pero ingenioso aparato es esencialmente un dispositivo para medir el cambio de volumen debido al derretimiento del hielo. Para medir una capacidad calorífica, se coloca una muestra caliente en el compartimiento interno, el cual está rodeado por una mezcla de hielo y agua.
El calor retirado de la muestra a medida que se enfría provoca que parte del hielo se derrita. Dado que el hielo es menos denso que el agua, el volumen de agua en la cámara aislada disminuye. Esto hace que un volumen equivalente de mercurio sea succionado hacia el depósito interno desde el contenedor exterior. La pérdida de peso de este recipiente da la disminución en el volumen del agua, y así la masa de hielo se fundió. Esto, combinado con el calor de fusión del hielo, da la cantidad de calor perdida por la muestra a medida que se enfría a 0°C.


