Teoría Cinético-Molecular
- Page ID
- 74872
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Habilidades para Desarrollar
- Definir la teoría cinético-molecular y su relación con la ecuación de gas ideal
La Ley de Boyle se publicó alrededor de 1660. En 1718, un matemático llamado Bernoulli propuso una explicación para la Ley de Boyle. Aunque esto fue casi cien años antes de la Teoría Atómica de Dalton, las teorías atomísticas (también llamadas a veces “teorías corpusculares”) habían existido por mucho tiempo. El propio Boyle había hecho algunos argumentos similares a los de Dalton que tomó prestados de Sennert. Bernoulli asumió que el gas estaba hecho de muchas partículas pequeñas que se movían rápidamente. Se mueven en línea recta hasta chocar con otra partícula o una pared, luego rebotan de acuerdo a la conservación del ímpetu. La presión proviene del impacto cuando estas partículas chocan contra las paredes.
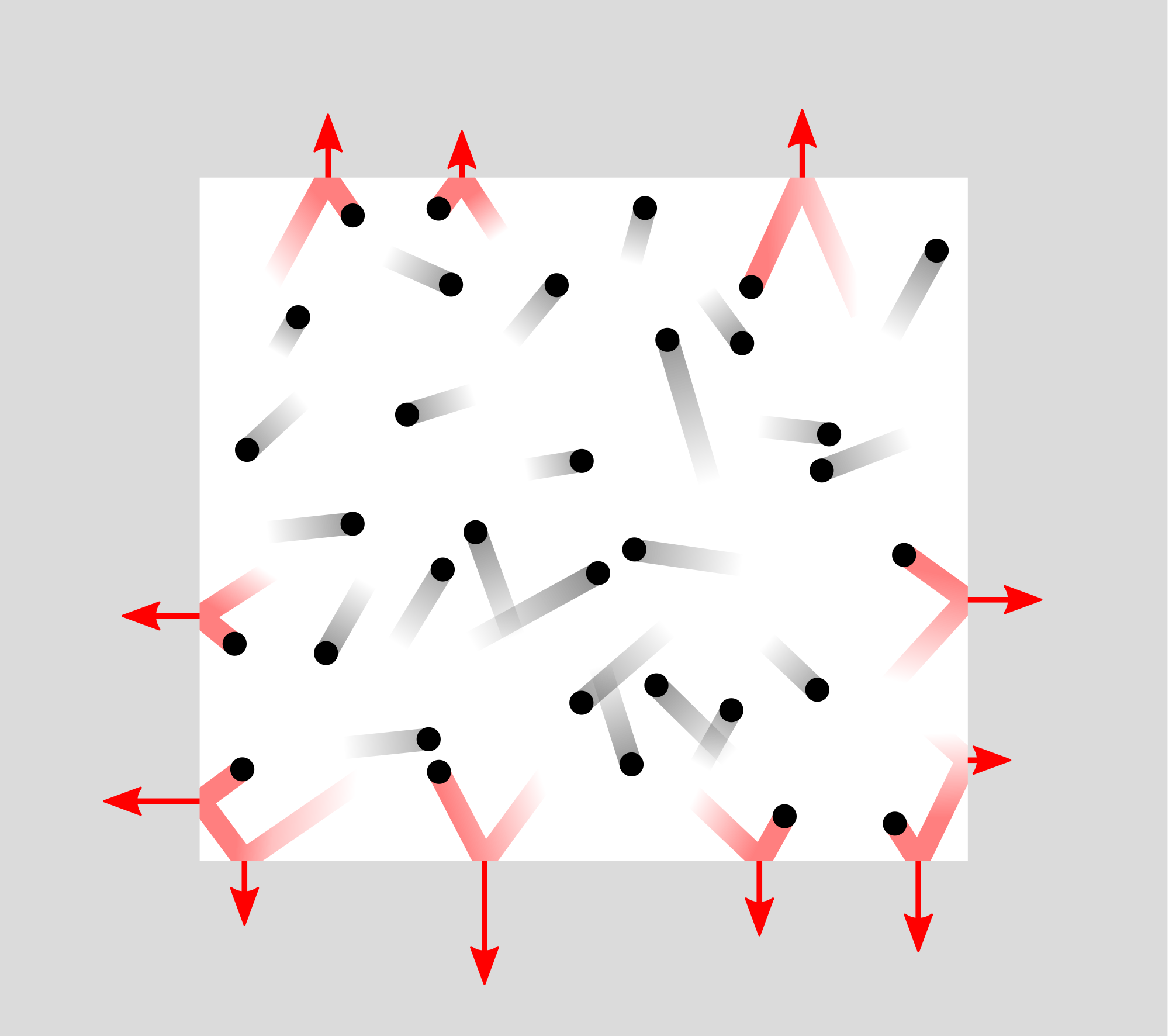
¿Cómo depende la presión del volumen? Bernoulli da esta explicación. Si comprimimos un gas, las partículas chocarán con más frecuencia las paredes. Esto sucede por 2 razones: primero, hay más partículas en la capa junto a la pared, donde pueden chocar con ella. En segundo lugar, las partículas que se alejan de la pared tienen más probabilidades de chocar con otra partícula, cambiar de dirección y volver a chocar con la pared. Imagínese que tenemos un contenedor cúbico, con cada longitud lateral s. si se disminuye el volumen de 1 a s 3, entonces el número de partículas en la capa junto a la pared aumenta en s 2 /1. Además, el número de colisiones entre las partículas de capa de pared y la pared aumenta en s/1. Combinando estos, el número de colisiones aumenta en s 3 cuando el volumen disminuye 1/s 3. La presión es el número de impactos multiplicado por el momento de las partículas, mv, donde m es la masa de una partícula y v es la velocidad promedio. Cuando se calcula el cambio de momento promedio de cada colisión y el número promedio de colisiones por área de pared, el resultado es P = nmv 2 /3V, donde n es el número de partículas y V es el volumen. Puedes ver que esto coincide con la Ley de Boyle: PV = nmv 2 /3 = constante. Posteriormente, se demostró que mv 2, la energía cinética, era proporcional a la temperatura: kT = mv 2. Esta es la ecuación de gas ideal.
¿Qué tan rápido se mueven las partículas de gas? Debido a que la energía cinética promedio es proporcional a la temperatura, los gases más pesados se mueven más lentamente que los gases ligeros a la misma temperatura. Habrá un gran rango de velocidades para diferentes moléculas, porque cambian de velocidad a medida que chocan entre sí. Para N 2 a 0 °C, el rango podría ser de 0-1300 m/s, con una velocidad promedio de aproximadamente 500 m/s. A medida que la temperatura aumenta, el rango aumenta y también lo hace la velocidad promedio. ¡Entonces las partículas suelen moverse muy rápido! ¿Hasta dónde van entre colisiones? Esto depende de las condiciones, pero la distancia promedio entre colisiones podría ser de 10 a 7 m, ¡así que no lejos!
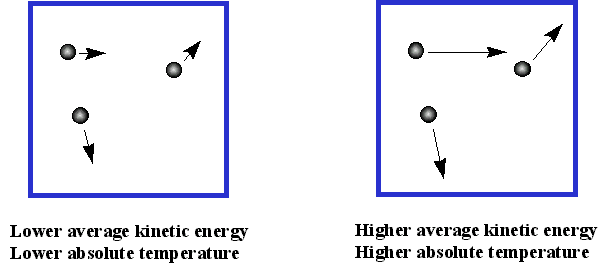
Así, imaginamos un gas como muchas partículas pequeñas que chocan entre sí perfectamente elásticamente (con conservación de impulso). Se comportan como bolitas duras, y no se atraen en absoluto. Su energía cinética depende de la temperatura. En la derivación de la ley del gas ideal, asumimos que no hay fuerzas atractivas entre las partículas y que las partículas no ocupan espacio alguno. Estas dos suposiciones son obviamente incorrectas: si no hay atracciones entre las partículas, no habría líquidos ni sólidos. De igual manera, las partículas sí ocupan un poco de espacio. Dado que sabemos que las fuerzas atractivas se vuelven importantes a bajas temperaturas, y que el volumen de las partículas será importante nosotros el volumen es relativamente bajo (es decir, la presión es alta) podemos predecir que la ecuación de gas ideal funciona mejor a altas temperaturas y bajas presiones.
Enlace exterior
Colaboradores y Atribuciones
Emily V Eames (City College of San Francisco)