Configuraciones de electrones
- Page ID
- 75005
Habilidades para Desarrollar
- Predecir e ilustrar configuraciones de electrones
Las funciones de onda en la sección anterior se derivaron solo para átomos de un solo electrón. Es realmente difícil, si no totalmente imposible, resolver perfectamente la ecuación de Schrodinger cuando hay 2 o más electrones, debido a las repulsiones electrón-electrón que hacen que el hamiltoniano sea increíblemente complicado. Sin embargo, resulta que podemos aproximar los orbitales en otros átomos con pequeñas modificaciones de las funciones de onda de hidrógeno, como disminuir la carga nuclear para dar cuenta de la repulsión de electrones.
Configuraciones de electrones
Bohr descubrió el número de electrones en cada caparazón, donde una concha son todos los electrones con el mismo número cuántico principal. El patrón que utilizó, que se puede verificar con la tabla periódica, fue de 2, 8, 8, 18, 18, 32, 32. Sin embargo, no fue tan claro sobre la disposición en subconchas, que son grupos de electrones con el mismo principio y números cuánticos de momento angular, como 1s o 2p. Esto se hizo mucho más claro después de que se introdujeron las funciones de onda de Schrodinger para el átomo de hidrógeno, ya que las funciones de onda de la solución claramente solo tenían ciertos valores de l permisibles y valores de m l. Aunque todos los orbitales de una concha tienen la misma energía en un solo átomo de electrones, cuando hay más electrones las subconchas tienen diferentes energías. Esto se debe a que cuanto mayor l está dentro de una concha, más lejos suele estar el electrón del núcleo. En los orbitales, los electrones suelen estar cerca del núcleo, por lo que otros electrones no bloquean mucho la carga nuclear. En los orbitales d y f, los electrones están lejos del núcleo y sí se bloquean. Así, los orbitales tienden a llenarse primero en el orden de la n más baja y la l más baja.
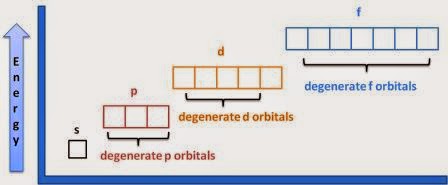
Los orbitales con la misma energía se llaman degenerados. (En otros contextos, degenerado significa inmoral, u otras cosas malas). En general, cuantas más complicaciones añadas, como más electrones, átomos vecinos, campos magnéticos, etc, menos orbitales se degeneran. Entonces, para un átomo de hidrógeno por sí mismo, todos los orbitales de cada caparazón son degenerados. Cuando te mueves a un átomo de helio solitario, los orbitales en las subconchas son degenerados. Cuando haces enlaces químicos, los orbitales en las subconchas ya no están degenerados. Cuando se aplica un campo magnético, los electrones en el mismo orbital no son degenerados.
Reglas simples para predecir configuraciones de electrones de átomos
¿Cómo predecir configuraciones de electrones para elementos? La configuración de electrones solo significa cuántos electrones hay en cada orbital. Necesitarás saber la cantidad de electrones que estás usando. Esto se puede obtener de la tabla periódica (el número atómico − carga si es un ion). O simplemente se te podría dar el número atómico. Si tienes una tabla periódica, es fácil, por la forma de la tabla. Si vas a la tabla periódica de este sitio, verás que tiene un bloque azul, un bloque rojo, un bloque amarillo y un bloque verde. El código es azul = s; amarillo = p; rojo = d; y verde = f Los metales alcalinos y alcalinotérreos tienen sus electrones de mayor energía en un orbital s. Los electrones de mayor energía, los que están en la capa más alta, se llaman electrones de valencia. El grupo principal (amarillo) incluyendo halógenos y gases nobles, tienen sus electrones más altos en orbitales p. Los metales de transición tienen los suyos en los orbitales d, y los lantanoides y actinoides en los orbitales f. Observe que cada sección tiene 2, 6, 10 o 14 elementos de ancho, porque hay 1,3,5,7 orbitales en las subcapas s, p, d y f, y cada orbital contiene 2 electrones. Entonces puedes escribir la configuración electrónica con solo mirar la tabla periódica. Sigue tu camino, escribiendo cuántos electrones hay en cada subcapa, hasta que tengas el número correcto de electrones en total. Por ejemplo, para Al, tendrías 1s 2 2s 2 2p 6 3s 2 3p 1. Observe que indicamos el número de electrones en cada subcapa usando superíndices escribimos configuraciones de electrones.
Otro truco que puedes usar para escribir configuraciones de electrones es seguir las flechas de este diagrama. El patrón de relleno se llama “aufbau” que significa “construir” en alemán, o eso he escuchado. Observe que en realidad no llena todos los subshells en un shell antes de pasar al siguiente. Esto puede ser un poco confuso (espcialmente porque los orbitales s son solo ligeramente más bajos que los orbitales d anteriores, ¡y en los iones el orden energético vuelve a retroceder!). O usa este diagrama o una tabla periódica, y obtendrás las respuestas correctas siempre y cuando tengas cuidado de contar desde la parte superior de la tabla periódica. Observe cómo la primera fila de d viene después de la 4ta fila de s? Pero podemos tener orbitales 3d, así que la primera fila de d es 3d, no 4d.
Muchas veces no queremos escribir todos los electrones para un átomo pesado, porque los internos son exactamente los mismos que todos los demás elementos. Entonces podríamos mostrar sólo los electrones de valencia, lo que significa en este caso los añadidos en esta fila de la tabla periódica, o después del último gas noble. Entonces podríamos escribir Ti como [Ar] 4s 2 3d 2, lo que solo significa que tiene la misma configuración que argon, + 4s 2 3d 2.
La siguiente pregunta viene cuando no se llenan todos los orbitales de un subshell. ¿Empareja electrones o los pones en orbitales separados? Por ejemplo, considere el carbono. Se puede representar su configuración electrónica así, con las flechas hacia arriba y hacia abajo representando el espín electrónico.
Pero, ¿cuál de las 3 posibilidades es? Recuerde que el espín electrónico se presentó en espectroscopía con campos magnéticos. Los electrones son como imanes diminutos, y cuando están emparejados (uno arriba, uno abajo) se cancelan entre sí y no parecen magnéticos a menos que te veas muy duro. Pero sabes que hay muchos materiales muy magnéticos por ahí (tal vez los uses en tu refrigerador; también los usas en auriculares y otros dispositivos). La razón por la que son magnéticos es porque el arreglo inferior es la energía más baja. Los electrones prefieren tener el mismo giro en diferentes orbitales, donde se repelen menos entre sí (entre otras razones más complicadas). Esto se llama Regla de Hund. La razón por la que los mejores imanes son metales de transición o lantanoides es que los orbitales d y f tienen espacio para extender 5 o 7 electrones con el mismo giro.
La única otra cosa que necesitas saber de las configuraciones de electrones en este momento es que hay algunas excepciones a las reglas sobre qué orden llenan (principalmente en los bloques d y f). Estos no son muy importantes. La otra cosa que quizás quieras saber es si la configuración electrónica en átomos aislados es importante para los químicos. En su mayoría solo los electrones de valencia se ven afectados por la unión, por lo que la configuración elemental probablemente seguirá aplicándose a los electrones centrales. Y las configuraciones de electrones atómicos coinciden con los patrones de reactividad en los que originalmente se basó la tabla periódica, así que eso es útil. La otra razón es que estas reglas aplican casi lo mismo a situaciones químicas reales. Incluso si los orbitales son orbitales moleculares más complicados (los estudiaremos más adelante) en lugar de orbitales atómicos, aún los llenas de menor a mayor y usas la regla de Hund.
Enlaces externos
Colaboradores y Atribuciones
Emily V Eames (City College of San Francisco)