12.E: Cinética (Ejercicios)
- Page ID
- 75528
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)12.1: Tasas de reacción química
Q12.1.1
¿Cuál es la diferencia entre la tasa promedio, la tasa inicial y la tasa instantánea?
- Solución
-
Primero, se debe definir una velocidad de reacción general para saber cuál es cualquier variación de una velocidad. La velocidad de reacción se define como la medida del cambio en la concentración de los reactivos o productos por unidad de tiempo. La velocidad de una reacción química no es constante y más bien cambia continuamente, y puede ser influenciada por la temperatura. La velocidad de una reacción se puede definir como la desaparición de cualquier reactivo o aparición de cualquier producto. Así, una velocidad promedio es la velocidad de reacción promedio durante un período de tiempo dado en la reacción, la velocidad instantánea es la velocidad de reacción en un momento dado específico durante la reacción, y la velocidad inicial es la velocidad instantánea al inicio mismo de la reacción (cuando el producto comienza a formarse).
La velocidad instantánea de una reacción se puede denotar como\[ \lim_{\Delta t \rightarrow 0} \dfrac{\Delta [concentration]}{\Delta t} \nonumber \]
Q12.1.2
El ozono se descompone en oxígeno según la ecuación\(\ce{2O3}(g)⟶\ce{3O2}(g)\). Escribe la ecuación que relaciona las expresiones de velocidad para esta reacción en términos de la desaparición de O 3 y la formación de oxígeno.
- Solución
-
Para la reacción general, aA —> bB, la velocidad de la reacción se puede expresar en términos de la desaparición de A o la aparición de B durante un cierto periodo de tiempo de la siguiente manera.
\[- \dfrac{1}{a}\dfrac{\Delta [A]}{\Delta t} = - \dfrac{1}{b}\dfrac{\Delta [B]}{\Delta t} = \dfrac{1}{c}\dfrac{\Delta [C]}{\Delta t} = \dfrac{1}{d}\dfrac{\Delta [D]}{\Delta t}\]
Queremos que la velocidad de una reacción sea positiva, pero el cambio en la concentración de un reactante, A, será negativo porque se está utilizando para transformarse en producto, B. Por lo tanto, al expresar la velocidad de la reacción en términos del cambio en la concentración de A, es importante agregar un signo negativo al frente para asegurar la tasa general positiva.
Por último, la velocidad debe normalizarse de acuerdo con la estequiometría de la reacción. En la descomposición del ozono a oxígeno, dos moles de ozono forman tres moles de gas oxígeno. Esto quiere decir que el incremento en el gas oxígeno será 1.5 veces mayor que la disminución del ozono. Debido a que la velocidad de reacción debería ser capaz de describir ambas especies, dividimos el cambio de concentración por su coeficiente estequiométrico en la ecuación de reacción equilibrada para tratar este problema.
Por lo tanto, la velocidad de reacción de la descomposición del ozono en gas oxígeno se puede describir de la siguiente manera:
\[Rate=-\frac{Δ[O3]}{2ΔT}=\frac{Δ[O2]}{3ΔT}\]
- Responder
-
$ Tasa =-\ frac {Δ [O3]} {2ΔT} =\ frac {Δ [O2]} {3ΔT}\]
Q12.1.3
En la industria nuclear, el trifluoruro de cloro se utiliza para preparar hexafluoruro de uranio, un compuesto volátil de uranio utilizado en la separación de isótopos de uranio. El trifluoruro de cloro se prepara por la reacción\(\ce{Cl2}(g)+\ce{3F2}(g)⟶\ce{2ClF3}(g)\). Escribe la ecuación que relaciona las expresiones de velocidad para esta reacción en términos de la desaparición de Cl 2 y F 2 y la formación de ClF 3.
- Solución
-
En este problema se nos pide escribir la ecuación que relaciona las expresiones de tasa en términos de desaparición de los reactivos de la ecuación y en términos de la formación del producto. Una velocidad de reacción da una idea de cómo se ve afectada la velocidad en función de la concentración de las sustancias en la ecuación. Las tasas a menudo se pueden expresar en gráficas de concentración vs tiempo expresadas en cambio (\({\Delta}\)) de concentración y tiempo y en un intervalo de tiempo lo suficientemente corto, se puede aproximar la tasa instantánea. Si analizáramos la reacción dada, la gráfica demostraría que Cl 2 disminuye, que F 2 disminuye 3 veces más rápido, y luego ClF 3 aumenta a una velocidad que se duplica. Los reactivos están siendo utilizados y convertidos en producto por lo que disminuyen mientras que los productos aumentan.
Para este problema, podemos aplicar la fórmula general de una tasa a los aspectos específicos de un problema donde la forma general sigue:\[aA+bB⟶cC+dD\nonumber \].
Y entonces la tasa se puede escribir como\(rate=-\frac {1}{a}\frac{{\Delta}[A]}{{\Delta}t}\)\(=-\frac {1}{b}\frac{{\Delta}[B]}{{\Delta}t}\)\(=\frac {1}{c}\frac{{\Delta}[C]}{{\Delta}t}\)\(=\frac {1}{d}\frac{{\Delta}[D]}{{\Delta}t}.\) Aquí se utilizan los signos negativos para mantener la convención de expresar tasas como números positivos.
En este caso concreto utilizamos la estequiometría para obtener las tasas específicas de desaparición y formación (volviendo a lo dicho en el primer párrafo). Entonces, el problema solo implica referir el a la ecuación y sus coeficientes equilibrados. Con base en la ecuación vemos que Cl 2 es un reactivo y no tiene coeficiente, F 2 tiene un coeficiente de 3 y también se agota, y luego ClF 3 es un producto que aumenta dos veces con un coeficiente de 2. Entonces, la tarifa aquí se puede escribir como:\[rate=-\frac{{\Delta}[Cl_2]}{{\Delta}t}=-\frac {1}{3}\frac{{\Delta}[F_2]}{{\Delta}t}=\frac {1}{2}\frac{{\Delta}[ClF_3]}{{\Delta}t}\nonumber \]
- Responder
-
\[\ce{rate}=+\dfrac{1}{2}\dfrac{Δ[\ce{CIF3}]}{Δt}=−\dfrac{Δ[\ce{Cl2}]}{Δt}=−\dfrac{1}{3}\dfrac{Δ[\ce{F2}]}{Δt}\nonumber \]
Q12.1.4
Un estudio de la tasa de dimerización de C 4 H 6 dio los datos mostrados en la tabla:
\[\ce{2C4H6⟶C8H12}\nonumber \]
| Tiempo (s) | 0 | 1600 | 3200 | 4800 | 6200 |
|---|---|---|---|---|---|
| [C 4 H 6] (M) | 1.00 × 10 −2 | 5.04 × 10 −3 | 3.37 × 10 −3 | 2.53 × 10 −3 | 2.08 × 10 −3 |
- Determinar la tasa promedio de dimerización entre 0 s y 1600 s, y entre 1600 s y 3200 s.
- Estimar la tasa instantánea de dimerización a 3200 s a partir de una gráfica de tiempo versus [C 4 H 6]. ¿Cuáles son las unidades de esta tarifa?
- Determinar la tasa promedio de formación de C 8 H 12 a 1600 s y la tasa instantánea de formación a 3200 s a partir de las tasas encontradas en las partes (a) y (b).
- Solución
-
1.) La tasa promedio de dimerización es el cambio en la concentración de un reactivo por unidad de tiempo. En este caso sería:
\(rate\)\(of\)\(dimerization=-\frac{\Delta [C_4H_6]}{\Delta t}\)
Tasa de dimerización entre 0 s y 1600 s:
\(rate\)\(of\)\(dimerization=-\frac{5.04×10^{-3}M-1.00×10^{-2}M}{1600 s-0 s}\)
\(rate\)\(of\)\(dimerization=3.10 × 10^{-6} \frac{M}{s}\)
Tasa de dimerización entre 1600 s y 3200 s:
\(rate\)\(of\)\(dimerization=-\frac{3.37×10^{-3}M-5.04×10^{-3}M}{3200 s-1600 s}\)
\(rate\)\(of\)\(dimerization=1.04 × 10^{-6} \frac{M}{s}\)
2.) La tasa instantánea de dimerización a 3200 s se puede encontrar graficando el tiempo versus [C 4 H 6].
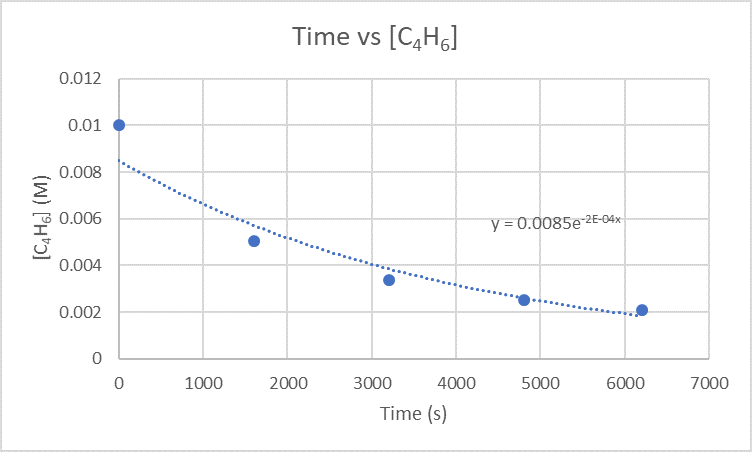
Debido a que quieres encontrar la tasa de dimerización a 3200 s, necesitas encontrar la pendiente entre 1600 s y 3200 s y también 3200 s y 4800 s.
Para la pendiente entre 1600 s y 3200 s usa los puntos (1600 s, 5.04 x 10 -3 M) y (3200 s, 3.37 x 10 -3 M)
\(\frac{3.37×10^{-3}M-5.04×10^{-3}M}{3200 s-1600 s}\)
\(\frac{-0.00167 M}{1600 s}\)
\(-1.04×10^{-6}\frac{M}{s}\)
Para la pendiente entre 3200 s y 4800 s usa los puntos (3200s, 3.37 x 10 -3 M) y (4800s, 2.53 x 10 -3 M)
\(\frac{2.53×10^{-3}M-3.37×10^{-3}M}{4800 s-3200 s}\)
\(\frac{-8.4×10^{-4} M}{1600 s}\)
\(-5.25×10^{-7}\frac{M}{s}\)
Toma las dos pistas que acabas de encontrar y encuentra el promedio de ellas para obtener la tasa instantánea de dimerización.
\(\frac{-1.04×10^{-6}\frac{M}{s}+-5.25×x10^{-7}\frac{M}{s}}{2}\)
\(\frac{-1.565×10^{-6}\frac{M}{s}}{2}\)
\(-7.83×10^-7\frac{M}{s}\)
La velocidad instantánea de dimerización es \(-7.83×10^-7\frac{M}{s}\)y las unidades de esta tasa son \(\frac{M}{s}\).
3.) La tasa promedio de formación de C 8 H 12 a 1600 s y la tasa instantánea de formación a 3200 s se puede encontrar usando nuestras respuestas de las partes a y b. Si miras hacia atrás en la ecuación original, podrías ver que C 4 H 6 y C 8 H 12 están relacionados en una proporción de dos a uno. Por cada dos moles de C 4 H 6 utilizados, se produce un mol de C 8 H 12.
Para esta reacción, la velocidad promedio de dimerización y la velocidad media de formación pueden vincularse a través de esta ecuación:
\(\frac{-1}{2}\frac{\Delta [C_4H_6]}{\Delta t}=\frac{\Delta [C_8H_{12}]}{\Delta t}\)
Observe que el lado reactivo es negativo porque los reactivos se están consumiendo en la reacción.
Entonces, para la tasa promedio de formación de C 8 H 12 a 1600 s, use la tasa de dimerización entre 0 s y 1600 s que encontramos anteriormente y conecte a la ecuación:
\(\frac{-1}{2}×3.10 × 10^{-6} \frac{M}{s}=\frac{\Delta [C_8H_{12}]}{\Delta t}\)
\(\frac{\Delta [C_8H_{12}]}{\Delta t}=1.55×10^{-6}\frac{M}{s}\)
La tasa media de formación para C 8 H 12 a 1600 s es\(1.55×10^{-6}\frac{M}{s}\). La tasa de formación será positiva porque se están formando productos.
La tasa instantánea de formación para C 8 H 12 puede vincularse a la velocidad instantánea de dimerización mediante esta ecuación:
\(\frac{-1}{2}\frac{d[C_4H_6]}{dt}=\frac{d[C_8H_{12}]}{dt}\)
Entonces, para la tasa instantánea de formación para C 8 H 12 a 3200 s, use el valor de velocidad instantánea de dimerización a 3200 s encontrado anteriormente y conecte a la ecuación:
\(\frac{-1}{2}×-7.83×10^-7\frac{M}{s}=\frac{d[C_8H_{12}]}{dt}\)
\(\frac{d[C_8H_{12}]}{dt}=-3.92×10^{-7}\frac{M}{s}\)
La tasa instantánea de formación para C 8 H 12 a 3200 s es\(-3.92×10^-7\frac{M}{s}\)
- Responder
-
- \(3.10 × 10^{-6} \frac{M}{s}\)y\(1.04 × 10^{-6} \frac{M}{s}\)
- \(-7.83×10^-7\frac{M}{s}\)y\(\frac{M}{s}\)
- \(-3.92×10^-7\frac{M}{s}\)
Q12.1.5
Un estudio de la velocidad de la reacción representada\(2A⟶B\) dio los siguientes datos:
| Tiempo (s) | 0.0 | 5.0 | 10.0 | 15.0 | 20.0 | 25.0 | 35.0 |
|---|---|---|---|---|---|---|---|
| [A] (M) | 1.00 | 0.952 | 0.625 | 0.465 | 0.370 | 0.308 | 0.230 |
- Determinar la tasa promedio de desaparición de A entre 0.0 s y 10.0 s, y entre 10.0 s y 20.0 s.
- Estimar la tasa instantánea de desaparición de A a 15.0 s a partir de una gráfica de tiempo versus [A]. ¿Cuáles son las unidades de esta tarifa?
- Utilizar las tasas encontradas en las partes (a) y (b) para determinar la tasa promedio de formación de B entre 0.00 s y 10.0 s, y la tasa instantánea de formación de B a 15.0 s.
- Solución
-
Ecuaciones:\(\frac{-\bigtriangleup A}{\bigtriangleup time}\) y Velocidad=\(\frac{-\bigtriangleup A}{2\bigtriangleup time}=\frac{\bigtriangleup B}{time}\)
Resolver: 1.) El cambio en A de 0s a 10s es de .625-1=-.375 así\(\frac{-\bigtriangleup A}{\bigtriangleup time}\) =.375/10= 0.0374 m/s
De igual manera, el cambio en A de 10 a 20 segundos es de .370-.625=-.255 así\(\frac{-\bigtriangleup A}{\bigtriangleup time}\) =.255/20-10= 0.0255m/s
2.) Podemos estimar la ley de tasas graficando los puntos contra diferentes ecuaciones de orden para determinar el orden correcto.
Orden Cero:\[\frac{d[A]}{dt}=-k\nonumber \]\[\int_{A_{\circ}}^{A}d[A]=-k\int_{0}^{t}dt\nonumber \]\[[A]=-kt+[A_{\circ}]\nonumber \]
Primer Pedido:\[\frac{d[A]}{dt}=-k[A]\nonumber \]\[\int_{A_{\circ}}^{A}\frac{d[A]}{[A]}=-kdt\nonumber \]\[Ln(A)=-kt+Ln(A_{\circ})\nonumber \]
Segundo Orden:\[\frac{d[A]}{dt}=-k[A]^{2}\nonumber \]\[\int_{A\circ}^{A}\frac{d[A]}{[A]^{2}}=-k\int_{0}^{t}dt\nonumber \]
\[\frac{1}{[A]}=kt+\frac{1}{[A_{\circ}]}\nonumber \]
Ahora que hemos encontrado el lineal de cada orden trazaremos los puntos vs un eje [A] y, un eje Ln (A) y, y un eje 1/ [A] y. Cualquiera de las parcelas que tenga más puntos lineales nos dará una buena idea del orden y la pendiente será el valor k.
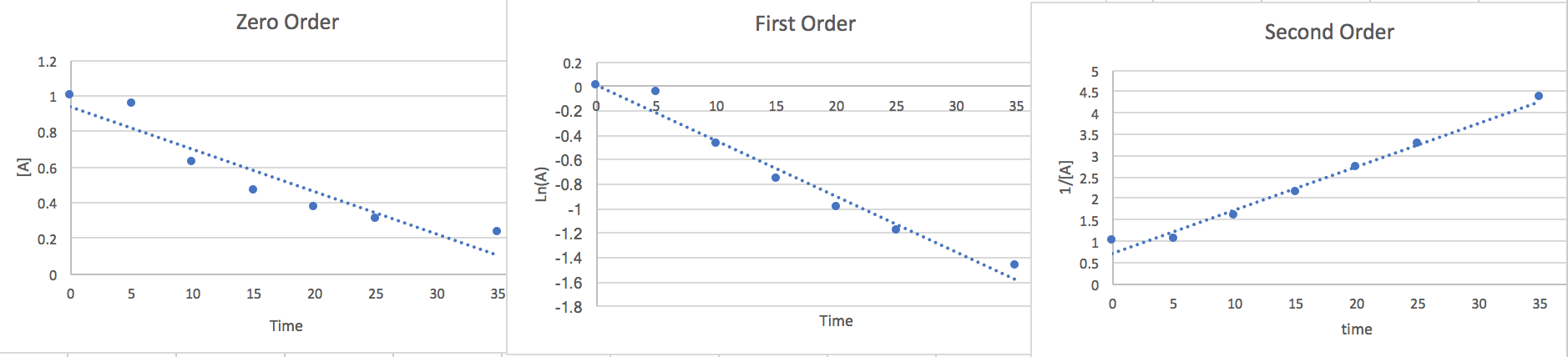
Aquí notamos que el segundo orden es más lineal por lo que concluimos la Tasa a ser.. \[\frac{-d[A]}{2dt}=k[A]^{2}\nonumber \]A los 15 segundos [A] =.465 y de la pendiente de la gráfica encontramos k=.116.así que si enchufamos estos datos y multiplicamos ambos lados por 2 para deshacernos del 2 en el denominador del lado izquierdo de la ecuación encontramos que la tasa de desaparición de A es .05 m/s donde las unidades son equivalentes a [mol*L -1 *s -1]
3.) Usando la ecuación\(\frac{-\bigtriangleup A}{2\bigtriangleup time}=\frac{\bigtriangleup B}{time}\) dividimos las tasas en la parte a y b a la mitad para obtener .0188 M/s de 0 a 10 segundos y .025 M/s para la tasa instantánea estimada a 15s.
- Responder
-
(a) tasa promedio, 0 − 10 s = 0.0375 mol L −1 s −1; tasa promedio, 12 − 18 s = 0.0225 mol L −1 s −1; (b) tasa instantánea, 15 s = 0.0500 mol L −1 s −1; (c) tasa promedio para la formación de B = 0.0188 mol L −1 s −1; tasa instantánea para la formación de B = 0.0250 mol L −1 s −1
Q12.1.6
Considere la siguiente reacción en solución acuosa:
\[\ce{5Br-}(aq)+\ce{BrO3-}(aq)+\ce{6H+}(aq)⟶\ce{3Br2}(aq)+\ce{3H2O}(l)\nonumber \]
Si la tasa de desaparición de Br — (aq) en un momento determinado durante la reacción es 3.5 × 10 −4 M s −1, ¿cuál es la tasa de aparición de Br 2 (aq) en ese momento?
- Solución
-
Paso 1. Definir la velocidad de la reacción.
Recordar:
Para la reacción general: aA + bB → cC+ dD
\(rate =- \frac{\Delta[A]}{a\Delta{t}}=- \frac{\Delta[B]}{b\Delta{t}}= \frac{\Delta[C]}{c\Delta{t}}=\frac{\Delta[D]}{d\Delta{t}}\)
Entonces, para la reacción:\(5Br^−(aq)+BrO^−_3(aq)+6H^+→3Br_2(aq)+3H_2O(l)\)
La tasa sería:\(rate =- \frac{\Delta[Br^-]}{5\Delta{t}}=- \frac{\Delta[BrO^-_3]}{\Delta{t}}= -\frac{\Delta[H^+]}{6\Delta{t}}=\frac{\Delta[Br_2]}{3\Delta{t}}=\frac{H_2O}{3\Delta{t}}\)
Paso 2. Ya que se nos da la tasa de desaparición de\(Br^-\) (aq) es\(3.5x10^-4 Ms^{-1}\), y queremos encontrar la tasa de aparición de\(Br_2\) (aq). Por lo tanto establecemos las dos tasas iguales entre sí.
\(rate =- \frac{\Delta[Br^-]}{5\Delta{t}}= \frac{\Delta[Br_2]}{3\Delta{t}}\)
Y,\(-\frac{\Delta[Br^-]}{\Delta{t}}= -3.5x10^{-4} Ms^{-1}\)
Entonces,\(3.5x10^{-4} Ms^{-1}\) =\(\frac{5}{3}\frac{\Delta[Br_2]}{\Delta{t}}\)
Paso 3. Ahora resuelve la ecuación.
\(\frac{(3.5x10^{-4})(3)}{5} = \frac{\Delta[Br_2]}{\Delta{t}}\)
\(\frac{\Delta[Br_2]}{\Delta{t}} = 2.1 x 10^{-4} Ms^{-1}\)
- Responder
-
\(\frac{\Delta[Br_2]}{\Delta{t}} = 2.1 x 10^{-4} Ms^{-1}\)
12.2: Factores que afectan las tasas de reacción
Q12.2.1
Describir el efecto de cada uno de los siguientes sobre la velocidad de reacción del magnesio metálico con una solución de ácido clorhídrico: la molaridad del ácido clorhídrico, la temperatura de la solución y el tamaño de las piezas de magnesio.
- Solución
-
Molaridad del Ácido Clorhídrico
- Las velocidades de reacción se ven afectadas por la frecuencia a la que las moléculas colisionan. Alta Molaridad = Alta Concentración lo que significa que hay más moléculas disponibles para colisionar así una reacción más rápida que una con una baja molaridad de HCl a un volumen fijo.
- Las temperaturas más altas aumentan la velocidad de reacción porque las moléculas se mueven más rápido, colisionando con mayor frecuencia
- el aumento de las temperaturas permite que más partículas pasen la barrera de energía de activación para iniciar la reacción
- la velocidad de reacción depende del tamaño del reactivo sólido; las piezas más pequeñas aumentan la posibilidad de colisión porque permiten una mayor área superficial, por lo tanto, una velocidad de reacción más rápida
Q12.2.2
Vaya al interactivo Reacciones y tarifas de PhET. Use la pestaña Colisión simple para representar cómo la colisión entre el oxígeno monatómico (O) y el monóxido de carbono (CO) resulta en la ruptura de un enlace y la formación de otro. Tire hacia atrás del émbolo rojo para liberar el átomo y observar los resultados. Después, haz clic en “Reload Launcher” y cambia a “Tiro en ángulo” para ver la diferencia.
- ¿Qué sucede cuando se cambia el ángulo de la colisión?
- Explique cómo esto es relevante para la velocidad de reacción.
- Solución
-
Según la teoría de las colisiones, hay muchos factores que provocan que ocurra una reacción, siendo tres de los factores la frecuencia con la que colisionan las moléculas o átomos, las orientaciones de las moléculas o átomos, y si hay suficiente energía para que ocurra la reacción. Entonces, si se cambia el ángulo del émbolo, el átomo que se dispara (un átomo de oxígeno solitario en este caso) golpeará la otra molécula (CO en este caso) en un punto diferente y en un ángulo diferente, por lo tanto, cambiar la orientación y el número de colisiones adecuadas probablemente no provocará que ocurra una reacción . Gracias a la simulación, podemos ver que esto es cierto: dependiendo del ángulo seleccionado, el átomo puede tardar mucho en chocar con la molécula y, cuando ocurre una colisión, puede que no resulte en la ruptura del enlace y la formación del otro (no ocurre reacción alguna).
En este caso particular, la velocidad de la reacción disminuirá porque, al cambiar el ángulo, las moléculas o átomos no colisionarán con la orientación correcta o tan a menudo con la orientación correcta.
Q12.2.3
En el interactivo Reacciones y tasas de PhET, utilice la pestaña “Muchas colisiones” para observar cómo interactúan múltiples átomos y moléculas bajo condiciones variables. Seleccione una molécula para bombear en la cámara. Establezca la temperatura inicial y seleccione las cantidades actuales de cada reactivo. Seleccione “Mostrar bonos” en Opciones. ¿Cómo afecta la velocidad de la reacción por la concentración y la temperatura?
S12.2.3
Con base en la Teoría de Colisiones, una reacción solo ocurrirá si las moléculas chocan con la orientación adecuada y con la energía suficiente requerida para que ocurra la reacción. La energía mínima con la que las moléculas deben colisionar se llama energía de activación (energía del estado de transición).
Al aumentar la concentración de reactivos se incrementa la probabilidad de que los reactivos colisionen en la orientación correcta ya que hay más reactivos en el mismo volumen de espacio. Por lo tanto, aumentar la concentración de reactivos aumentaría la velocidad de la reacción. Disminuir la concentración de reactivos disminuiría la velocidad de reacción debido a que el número total de posibles colisiones disminuiría.
La temperatura está directamente relacionada con la energía cinética de las moléculas y la energía de activación\(E_a\) es la energía mínima requerida para que ocurra una reacción y no cambia para una reacción. El aumento de la temperatura aumenta la energía cinética de los reactivos, lo que significa que los reactivos se moverán más rápido y chocarán entre sí con mayor frecuencia. Por lo tanto, al aumentar la temperatura se incrementa la velocidad de la reacción. Disminuir la temperatura disminuye la velocidad de reacción ya que las moléculas tendrán menos energía cinética, se moverán más despacio y, por lo tanto, colisionarán entre sí con menos frecuencia.
Q12.2.4
En el interactivo PhET Reactions & Rates, en la pestaña Many Collisions, configura una simulación con 15 moléculas de A y 10 moléculas de BC. Seleccione “Mostrar bonos” en Opciones.
- Deje la Temperatura Inicial en la configuración predeterminada. Observe la reacción. ¿La velocidad de reacción es rápida o lenta?
- Haga clic en “Pausar” y luego en “Restablecer todo”, y luego ingrese 15 moléculas de A y 10 moléculas de BC una vez más. Seleccione “Mostrar bonos” en Opciones. Esta vez, aumentar la temperatura inicial hasta que, en la gráfica, la línea de energía promedio total esté completamente por encima de la curva de energía potencial. Describa lo que sucede con la reacción.
- Solución
-
a. en la simulación, seleccionamos la configuración por defecto y la reacción A+BC. En la configuración predeterminada, vemos colisiones frecuentes, una temperatura inicial baja y una energía promedio total inferior a la energía de activación. La teoría de colisiones establece que la velocidad de una reacción es directamente proporcional a (la fracción de moléculas con orientación requerida), (fracciones de colisiones con energía requerida) y (frecuencia de colisión). Aunque vemos reactivos en movimiento y frecuentemente colisionando, la velocidad de la reacción directa en realidad es lenta porque tarda mucho tiempo para que los productos, AB y C, comiencen a aparecer. Esto se debe principalmente a que las fracciones de colisiones con la energía requerida son bajas, viniendo de que la energía promedio de las moléculas sea menor que la energía de activación.
b. La reacción procede a una velocidad aún más rápida. Nuevamente, la teoría de colisiones establece que la velocidad de una reacción es directamente proporcional a (la fracción de moléculas con orientación requerida), (fracciones de colisiones con energía requerida) y (frecuencia de colisión). Debido a que las moléculas tienen una mayor cantidad de energía, tienen más energía cinética. Con una mayor energía cinética, las moléculas no solo chocan más sino que también aumentan en la fracción de colisión. Sin embargo, la reacción hacia adelante y la reacción hacia atrás proceden a una velocidad rápida, por lo que ambas ocurren casi simultáneamente. Se necesita un tiempo más corto para que ocurran ambas reacciones. Con ambas reacciones sumando en general, eventualmente hay un estado de equilibrio. El proceso en el que se alcanza el equilibrio, sin embargo, es más rápido. Por lo tanto, la cantidad de productos de A+BC se mantiene igual al cabo de un tiempo.
12.3: Leyes de tarifas
Q12.3.1
¿En qué se diferencian la velocidad de una reacción y su constante de velocidad?
S12.3.1
La velocidad de una reacción o velocidad de reacción es el cambio en la concentración del reactivo o del producto durante un periodo de tiempo. Si las concentraciones cambian, la tasa también cambia.
Tarifa para A → B:
La constante de velocidad (k) es una constante de proporcionalidad que relaciona las velocidades de reacción con los reactivos. Si las concentraciones cambian, la constante de velocidad no cambia.
Para una reacción con la ecuación general:\(aA+bB→cC+dD \)
la ley tarifaria determinada experimentalmente suele tener la siguiente forma:
Q12.3.2
Duplicar la concentración de un reactivo aumenta la velocidad de una reacción cuatro veces. Con este conocimiento, conteste las siguientes preguntas:
- ¿Cuál es el orden de la reacción con respecto a ese reactivo?
- Triplicar la concentración de un reactivo diferente aumenta la velocidad de una reacción tres veces. ¿Cuál es el orden de la reacción con respecto a ese reactivo?
- Solución
-
a) 2; b) 1
Q12.3.3
Triplicar la concentración de un reactivo aumenta la velocidad de una reacción nueve veces. Con este conocimiento, conteste las siguientes preguntas:
- ¿Cuál es el orden de la reacción con respecto a ese reactivo?
- Al aumentar la concentración de un reactivo por un factor de cuatro, aumenta la velocidad de una reacción cuatro veces. ¿Cuál es el orden de la reacción con respecto a ese reactivo?
Q12.3.4
¿Cuánto y en qué dirección afectará cada uno de los siguientes a la velocidad de la reacción:\(\ce{CO}(g)+\ce{NO2}(g)⟶\ce{CO2}(g)+\ce{NO}(g)\) si la ley de velocidad para la reacción es\(\ce{rate}=k[\ce{NO2}]^2\)?
- Disminuyendo la presión de NO 2 de 0.50 atm a 0.250 atm.
- Incrementar la concentración de CO de 0.01 M a 0.03 M.
- Solución
-
a) El proceso reduce la tasa en un factor de 4. b) Dado que el CO no aparece en la ley de tarifas, la tasa no se ve afectada.
Q12.3.5
¿Cómo afectará cada uno de los siguientes a la velocidad de la reacción:\(\ce{CO}(g)+\ce{NO2}(g)⟶\ce{CO2}(g)+\ce{NO}(g)\) si la ley de velocidad para la reacción es\(\ce{rate}=k[\ce{NO2}][\ce{CO}]\)?
- Aumentando la presión de NO 2 de 0.1 atm a 0.3 atm
- Incrementar la concentración de CO de 0.02 M a 0.06 M.
Q12.3.6
Los vuelos regulares de aviones supersónicos en la estratosfera son motivo de preocupación porque tales aeronaves producen óxido nítrico, NO, como subproducto en los gases de escape de sus motores. El óxido nítrico reacciona con el ozono, y se ha sugerido que esto podría contribuir al agotamiento de la capa de ozono. La reacción\(\ce{NO + O3⟶NO2 + O2}\) es de primer orden con respecto tanto al NO como al O 3 con una constante de velocidad de 2.20 × 10 7 L/mol/s. ¿Cuál es la tasa instantánea de desaparición de NO cuando [NO] = 3.3 × 10 −6 M y [O 3] = 5.9 × 10 −7 M ?
- Solución
-
4.3 × 10 −5 mol/l/s
Q12.3.7
El fósforo radiactivo se utiliza en el estudio de los mecanismos de reacción bioquímica porque los átomos de fósforo son componentes de muchas moléculas bioquímicas. La ubicación del fósforo (y la ubicación de la molécula en la que está unida) se puede detectar a partir de los electrones (partículas beta) que produce:
\[\ce{^{32}_{15}P⟶^{32}_{16}S + e-}\nonumber \]
Tasa = 4.85 × 10 −2\(\mathrm{day^{-1}\:[^{32}P]}\)
¿Cuál es la tasa instantánea de producción de electrones en una muestra con una concentración de fósforo de 0.0033 M?
Q12.3.8
La constante de velocidad para la desintegración radiactiva de 14 C es de 1.21 × 10 −4 año −1. Los productos de la desintegración son átomos de nitrógeno y electrones (partículas beta):
\[\ce{^6_{14}C⟶^{6}_{14}N + e-}\nonumber \]
\[\ce{rate}=k[\ce{^6_{14}C}]\nonumber \]
¿Cuál es la tasa instantánea de producción de átomos de N en una muestra con un contenido de carbono 14 de 6.5 × 10 −9 M?
- Solución
-
7.9 × 10 −13 mol/L/año
Q12.3.9
¿Cuál es la tasa instantánea de producción de átomos de N Q12.3.8 en una muestra con un contenido de carbono-14 de 1.5 × 10 −9 M?
Q12.3.10
La descomposición del acetaldehído es una reacción de segundo orden con una constante de velocidad de 4.71 × 10 −8 L/mol/s. ¿Cuál es la velocidad instantánea de descomposición del acetaldehído en una solución con una concentración de 5.55 × 10 −4 M?
Q12.3.11
El alcohol se elimina del torrente sanguíneo por una serie de reacciones metabólicas. La primera reacción produce acetaldehído; luego se forman otros productos. Se han determinado los siguientes datos para la tasa a la que se extrae el alcohol de la sangre de un varón promedio, aunque las tasas individuales pueden variar entre 25 y 30%. Las mujeres metabolizan el alcohol un poco más lentamente que los hombres:
| [C 2 H 5 OH] (M) | 4.4 × 10 −2 | 3.3 × 10 −2 | 2.2 × 10 −2 |
|---|---|---|---|
| Tasa (mol/L/h) | 2.0 × 10 −2 | 2.0 × 10 −2 | 2.0 × 10 −2 |
Determinar la ecuación de velocidad, la constante de velocidad y el orden general de esta reacción.
- Solución
-
tasa = k; k = 2.0 × 10 −2 mol/L/h (aproximadamente 0.9 g/l/h para el macho promedio); La reacción es de orden cero.
Q12.3.12
Bajo ciertas condiciones, la descomposición del amoníaco sobre una superficie metálica da los siguientes datos:
| [NH 3] (M) | 1.0 × 10 −3 | 2.0 × 10 −3 | 3.0 × 10 −3 |
|---|---|---|---|
| Tasa (mol/L/h 1) | 1.5 × 10 −6 | 1.5 × 10 −6 | 1.5 × 10 −6 |
Determinar la ecuación de velocidad, la constante de velocidad y el orden general de esta reacción.
Q12.3.13
El cloruro de nitrosil, NOCl, se descompone en NO y Cl 2.
\[\ce{2NOCl}(g)⟶\ce{2NO}(g)+\ce{Cl2}(g)\nonumber \]
Determine la ecuación de velocidad, la constante de velocidad y el orden general de esta reacción a partir de los siguientes datos:
| [NOCL] (M) | 0.10 | 0.20 | 0.30 |
|---|---|---|---|
| Tasa (mol/L/h) | 8.0 × 10 −10 | 3.2 × 10 −9 | 7.2 × 10 −9 |
- Solución
-
Antes de que podamos averiguar primero la constante de tasa, primero debemos determinar la ecuación de tasa básica y el orden de tasa. La ecuación de velocidad básica para esta reacción, donde n es el orden de velocidad de NOCl y k es la constante de velocidad, es
\[rate = k[NOCl]^n\nonumber \]
ya que el NOCl es el reactivo en la reacción.
Para averiguar el orden de la reacción debemos encontrar el orden de [NoCl] ya que es el único reactivo en la reacción. Para ello debemos examinar cómo cambia la velocidad de la reacción a medida que cambia la concentración de NOCl.
Como [NoCl] duplica en concentración de 0.10 M a 0.20 M la tasa va de 8.0 x 10 -10 a 3.2 x 10 -9
(3.2 x 10 -9 (mol/L/h))/(8.0 x 10 -10 (mol/L/h)) = 4
por lo que concluimos que a medida que [NoCL] se duplica, la tasa sube en 4. Desde 2 2 = 4 podemos decir que el orden de [NoCL] es 2 por lo que nuestra ley de tarifas actualizada es
\[rate = k[NOCl]^2\nonumber \]
Ahora que tenemos el orden, podemos sustituir los primeros valores experimentales de la tabla dada para encontrar la constante de velocidad, k
(8.0 x 10 -10 (mol/L/h)) = k (0.10 M) 2 así
\[k= \dfrac{8.0 \times 10^{-10}}{ (0.10\, M)^2} = 8 \times 10^{-8} M^{-1} sec^{-1}\nonumber \]
Pudimos encontrar las unidades de k usando orden de tasa, cuando el orden de tasa es de 2 unidades de k son M -1 x seg -1
Entonces la ecuación de tasa es: tasa = k [NoCl] 2, es de segundo orden, y k = 8 x 10 -8 M -1 x seg -1
Ley general de tarifas:\[rate = \underbrace{(8 \times 10^{-8})}_{\text{1/(M x sec)}} [NOCl]^2\nonumber \]
- Responder
-
tasa = k [NOCl] 2; k = 8.0 × 10 −8 L/mol/s; segundo orden
Q12.3.14
A partir de los siguientes datos, determinar la ecuación de velocidad, la constante de velocidad y el orden con respecto a A para la reacción\(A⟶2C\).
| [A] (M) | 1.33 × 10 −2 | 2.66 × 10 −2 | 3.99 × 10 −2 |
|---|---|---|---|
| Tasa (mol/L/h) | 3.80 × 10 −7 | 1.52 × 10 −6 | 3.42 × 10 −6 |
- Solución
-
A. Usando los datos experimentales, podemos comparar los efectos de cambiar [A] en la velocidad de reacción relacionando proporciones de [A] con relaciones de velocidades
\[ \frac{2.66 \times 10^{-2}}{1.33 \times 10^{-2}} = 2\nonumber \]y\[ \frac{1.52 \times 10^{-6}}{3.8 \times 10^{-7}} = 4\nonumber \]
B. De esto sabemos que duplicar la concentración de A resultará en cuadruplicar la velocidad de reacción. El orden de esta reacción es 2.
C. Ahora podemos escribir la ecuación de tasa ya que conocemos el orden:
\[rate=k[A]^2\nonumber \]
D. Al conectar un conjunto de datos experimentales en nuestra ecuación de tasa podemos resolver para la constante de velocidad, k:
\[3.8 \times 10^{-7} = k \times (1.33 \times 10^{-2})^{2}\nonumber \]
\[k = \frac{3.8 \times 10^{-7}}{1.769 \times 10^{-4}}\nonumber \]
\[k= .00215 M^{-1}s^{-1}\nonumber \]
- Responder
-
\(k= .00215 M^{-1}s^{-1}\)
2do Orden
Q12.3.15
El óxido de nitrógeno (II) reacciona con el cloro según la ecuación:
\[\ce{2NO}(g)+\ce{Cl2}(g)⟶\ce{2NOCl}(g)\nonumber \]
Se han observado las siguientes velocidades iniciales de reacción para ciertas concentraciones de reactivos:
| [NO] (mol/L 1) | [Cl 2] (mol/L) | Tasa (mol/L/h) |
|---|---|---|
| 0.50 | 0.50 | 1.14 |
| 1.00 | 0.50 | 4.56 |
| 1.00 | 1.00 | 9.12 |
¿Cuál es la ecuación de tasa que describe la dependencia de la tasa de las concentraciones de NO y Cl 2? ¿Cuál es la constante de tasa? ¿Cuáles son los órdenes con respecto a cada reactivo?
- Solución
-
Para la ecuación general,
\(aA + bB \rightarrow cC + dD\)
La tarifa se puede escribir como
\(rate = k[A]^{m}[B]^{n}\)donde k es la constante de velocidad, y m y n son los órdenes de reacción.
Para nuestra ecuación
\(2NO(g) + Cl_{2}(g) \rightarrow 2NOCl(g)\)
el\(rate = k[NO]^{m}[Cl_{2}]^{n}\)
Ahora, necesitamos encontrar las órdenes de reacción. Los órdenes de reacción solo se pueden encontrar a través de valores experimentales. Podemos comparar dos reacciones donde uno de los reactivos tiene la misma concentración para ambos ensayos, y resolver para el orden de reacción.
\(\frac{rate_{1}}{rate_{2}}=\frac{[NO]_{1}^{m}[Cl_{2}]_{1}^{n}}{[NO]_{2}^{m}[Cl_{2}]_{2}^{n}}\)
Podemos utilizar los datos en la tabla proporcionada. Si enchufamos los valores para las filas 1 y 2, vemos que los valores para la concentración de Cl se cancelarán, dejando solo las tasas y las concentraciones de NO.
\(\frac{1.14}{4.56}=\frac{[0.5]^{m}}{[1.0]^{m}}\)
Ahora podemos resolver para m, y encontramos que m =2. Esto significa que el orden de reacción para [NO] es 2.
Ahora debemos encontrar el valor de n. Para ello, podemos usar la misma ecuación pero con los valores de las filas 2 y 3. Esta vez, la concentración de NO se cancelará.
\(\frac{4.56}{9.12}=\frac{[0.5]^{n}}{[1.0]^{n}}\)
Cuando resolvemos para n, encontramos que n = 1. Esto significa que el orden de reacción para [Cl 2] es 1.
Estamos un paso más cerca de terminar nuestra ecuación de tarifas.
\(rate = k[NO]^{2}[Cl_{2}]\)
Finalmente, podemos resolver para la constante de tasa. Para ello, podemos usar uno de los ensayos del experimento, y enchufar los valores para la velocidad, y concentraciones de reactivos, luego resolver para k.
\(1.14 mol/L/h = k[0.5 mol/L]^{2}[0.5mol/L]\)
\(k=9.12L^{2}mol^{-2}h^{-1}\)
Entonces, nuestra ecuación de tasa final es:
\(rate = (9.12 L^{2} mol^{-2}h^{-1})[NO]^{2}[Cl_{2}]\)
*Un error común es olvidar unidades. Asegúrese de realizar un seguimiento de sus unidades durante todo el proceso de determinación de su constante de tarifa. Tenga cuidado porque las unidades cambiarán en relación con el orden de reacción.
- Responder
-
tasa = k [NO] 2 [Cl] 2; k = 9.12 L 2 mol −2 h −1; segundo orden en NO; primer orden en Cl 2
Q12.3.17
El hidrógeno reacciona con el monóxido de nitrógeno para formar monóxido de dinitrógeno (gas de risa) de acuerdo con la ecuación:
\[\ce{H2}(g)+\ce{2NO}(g)⟶\ce{N2O}(g)+\ce{H2O}(g)\nonumber \]
Determine la ecuación de velocidad, la constante de velocidad y los órdenes con respecto a cada reactivo a partir de los siguientes datos:
| [NO] (M) | 0.30 | 0.60 | 0.60 |
|---|---|---|---|
| [H 2] (M) | 0.35 | 0.35 | 0.70 |
| Tasa (mol/l/s) | 2.835 × 10 −3 | 1.134 × 10 −2 | 2.268 × 10 −2 |
- Solución
-
Determinar la ecuación de velocidad, la constante de velocidad y los órdenes con respecto a cada reactivo.
La constante de tasa y las órdenes se pueden determinar a través de la ley de tasa diferencial. A continuación se da la forma general de la ley de tasa diferencial:
aA + bB + cC ==> productos
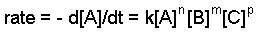
donde A, B y C son las concentraciones de los reactivos, k es la constante de velocidad y n, m y p se refieren al orden de cada reactivo.
Para encontrar los órdenes de cada reactivo, vemos que cuando [NO] se duplica pero [H 2] no cambia, la tasa se cuadruplica, lo que significa que [NO] es una reacción de segundo orden ([NO] 2). Cuando [H 2] duplica pero [NO] no cambia, la tasa se duplica, lo que significa que [H 2] es una reacción de primer orden. Entonces la ley tarifaria se vería así:
Tasa = k [NO] 2 [H 2]
Podemos usar esta ley de tarifas para determinar el valor de la constante de tasa. Conecte los datos para la concentración de reactivos y la velocidad de uno de los ensayos para resolver para k la constante de velocidad. En este caso, optamos por utilizar los datos del ensayo 1 de la segunda columna de la tabla de datos.
2.835x10 -3 = k [0.3] 2 [0.35]
k = .09 M -2 /s -1
Q12.3.18
Para la reacción\(A⟶B+C\), se obtuvieron los siguientes datos a 30 °C:
| [A] (M) | 0.230 | 0.356 | 0.557 |
|---|---|---|---|
| Tasa (mol/l/s) | 4.17 × 10 −4 | 9.99 × 10 −4 | 2.44 × 10 −3 |
- ¿Cuál es el orden de la reacción con respecto a [A], y cuál es la ecuación de tasa?
- ¿Cuál es la constante de tasa?
- Solución
-
1. La ecuación de velocidad para una reacción de\(n\) orden se da como\(\frac{dr}{dt}={k}{[A]^n}\). Dónde\([A]\) está la concentración en M, y\(\frac{dr}{dt}\) es la tasa en M/s.
Luego podemos usar cada conjunto de puntos de datos, enchufar sus valores en la ecuación de tasa y resolver para\(n\). Tenga en cuenta que puede utilizar cualquiera de los puntos de datos siempre y cuando la concentración corresponda a su tasa.
Ecuación de tasa 1:\(4.17 \times {10}^{-4}={k}{[0.230]^n}\)
Ecuación de tasa 2:\(9.99 \times {10}^{-4}={k}{[0.356]^n}\)
Dividimos la ecuación de tasa 1 por la ecuación de tasa 2 para cancelar k, la constante de velocidad.
\({\frac{4.17 \times {10}^{-4}}{9.99 \times {10}^{-4}}} = {\frac{k[0.230]^n}{k[0.356]^n}} \)
\({0.417}={0.646^n}\)
Ahora lo único desconocido que tenemos es\(n\). Usando reglas de logaritmo se puede resolver por ello.
\(ln{\: 0.417}={n \cdot ln{\: 0.646}}\)
\(\frac{ln{\: 0.417}}{ln{\:0.646}}=n=2\)
La ecuación de tasa es de segundo orden con respecto a A y se escribe como\(\frac{dr}{dt}={k}{[A]^2}\).
2. Podemos resolver\(k\) por enchufar cualquier punto de datos en nuestra ecuación de tasa\(\frac{dr}{dt}={k}{[A]^2}\).
Usando los primeros puntos de datos por ejemplo\( [A]=0.230 \:\frac{mol}{L}\) y\( \frac{dr}{dt} = 4.17 \times {10}^{-4} \:\frac{mol}{L \cdot s}\)] obtenemos la ecuación\(4.17 \times {10}^{-4} \:\frac{mol}{L \cdot s}={k}{[0.230 \:\frac{mol}{L}]^2}\)
Que resuelve para\(k=7.88 \times {10}^{-3} \frac{L}{mol \cdot s}\)
Como sabemos que esta es una reacción de segundo orden las unidades apropiadas para también se\(k\) pueden escribir como\( \frac{1}{M \cdot s}\)
- Responder
-
(a) La ecuación de tasa es de segundo orden en A y se escribe como tasa = k [A] 2. (b) k = 7.88 × 10 −13 L mol −1 s −1
Q12.3.19
Para la reacción\(Q⟶W+X\), se obtuvieron los siguientes datos a 30 °C:
| [Q] inicial (M) | 0.170 | 0.212 | 0.357 |
|---|---|---|---|
| Tasa (mol/l/s) | 6.68 × 10 −3 | 1.04 × 10 −2 | 2.94 × 10 −2 |
- ¿Cuál es el orden de la reacción con respecto a [Q], y cuál es la ecuación de tasa?
- ¿Cuál es la constante de tasa?
- Solución
-
¿Cuál es el orden de la reacción con respecto a [Q], y cuál es la ecuación de tasa?
- Reacción de pedido: 2 porque cuando usas la prueba de ratio 3:2, se verá así:
- (\(\dfrac{2.94*10^{-2}}{1.04*10^{-2}}\)) = (\(\dfrac{0.357^{x}}{0.212^{x}}\))
- 2.82 = 1.7 x
- x = 2 entonces el orden de reacción es 2
- Ecuación de velocidad de reacción: Tasa = K [Q] 2
- Para encontrar la constante de velocidad (k) simplemente conecte y calcule uno de los ensayos en la ecuación de tasa
- 1.04 x 10 -2 =k [0.212] 2
- k=0.231\(M^{-1}s^{-1}\)
- Responder
-
Orden: 2
k=0.231\(M^{-1}s^{-1}\)
Q12.3.20
La constante de velocidad para la descomposición de primer orden a 45 °C del pentóxido de dinitrógeno, N 2 O 5, disuelto en cloroformo, CHCl 3, es 6.2 × 10 −4 min −1.
\[\ce{2N2O5⟶4NO2 + O2}\nonumber \]
¿Cuál es la velocidad de reacción cuando [N 2 O 5] = 0.40 M?
- Solución
-
Paso 1: El primer paso es escribir la ley de tarifas. Conocemos la fórmula general para una ley de primer orden. Es el siguiente: Rate=K [A]
Paso 2: Ahora conectamos [N 2 O 5] para [A] en nuestra ley general de tarifas. También enchufamos nuestra constante de tasa (k), que nos fue dada. Ahora nuestra ecuación se ve de la siguiente manera:
Velo= (6.2x10 -4 min -1) [N 2 O 5]
Paso 3: Ahora enchufamos nuestra molaridad dada. [N 2 O 5] =0.4 M. Ahora nuestra ecuación se ve de la siguiente manera:
Velo= (6.2x10 -4 min -1) (0.4 M)
Paso 4: Ahora resolvemos nuestra ecuación. Calidad= (6.2x10 -4 min -1) (0.4 M) = 2.48x10 -4 m/Min.
Paso 5: Usar cifras significativas y conversión de unidades a redondo 2.48x10 -4 M/min a 2.5 × 10 −4 (moles) L -1 min -1
- Responder
-
(a) 2.5 × 10 −4 mol/L/min
Q12.3.21
La producción anual de HNO 3 en 2013 fue de 60 millones de toneladas métricas La mayor parte de eso se preparó mediante la siguiente secuencia de reacciones, cada una ejecutada en un recipiente de reacción separado.
- \(\ce{4NH3}(g)+\ce{5O2}(g)⟶\ce{4NO}(g)+\ce{6H2O}(g)\)
- \(\ce{2NO}(g)+\ce{O2}(g)⟶\ce{2NO2}(g)\)
- \(\ce{3NO2}(g)+\ce{H2O}(l)⟶\ce{2HNO3}(aq)+\ce{NO}(g)\)
La primera reacción se realiza quemando amoníaco en aire sobre un catalizador de platino. Esta reacción es rápida. La reacción en la ecuación (c) también es rápida. La segunda reacción limita la velocidad a la que se puede preparar el ácido nítrico a partir del amoníaco. Si la ecuación (b) es de segundo orden en NO y de primer orden en O 2, ¿cuál es la tasa de formación de NO 2 cuando la concentración de oxígeno es de 0.50 M y la concentración de óxido nítrico es de 0.75 M? La constante de velocidad para la reacción es 5.8 × 10 −6 L 2 /mol 2 /s.
- Solución
-
Para determinar la ley de tasas para una ecuación necesitamos mirar su paso lento. Dado que tanto la ecuación a como la c son rápidas, la ecuación b puede considerarse el paso lento de la reacción. El paso lento también se considera el paso determinante de la velocidad del sistema.
De ahí, El paso determinante de la tasa es el segundo paso porque es el paso lento.
tasa de producción de\(NO_2 = k [A]^m [B]^n \)
\(rate = k [NO]^2 [O_2]^1~M/s\)
\(rate = (5.8*10^{-6}) [0.75]^2 [0.5]^1 ~M/s\)
\(rate = 1.6*10^{-6}~M/s\)
- Responder
-
\(rate = 1.6*10^{-6}~M/s\)
Q12.3.22
Se han determinado los siguientes datos para la reacción:
\[\ce{I- + OCl- ⟶ IO- + Cl-}\nonumber \]
| 1 | 2 | 3 | |
|---|---|---|---|
| \(\mathrm{[I^-]_{initial}}\)(M) | 0.10 | 0.20 | 0.30 |
| \(\mathrm{[OCl^-]_{initial}}\)(M) | 0.050 | 0.050 | 0.010 |
| Tasa (mol/l/s) | 3.05 × 10 −4 | 6.20 × 10 −4 | 1.83 × 10 −4 |
Determinar la ecuación de velocidad y la constante de velocidad para esta reacción.
- Solución
-
Usando los reactivos, podemos formar la ley de velocidad de la reacción: $ r=k [OCl^-] ^n [I^-] ^m\]
A partir de ahí, necesitamos usar los datos para determinar el orden de ambos\([OCl^-]\) y\([I^-]\). Al hacerlo, necesitamos\(r_1\) compararnos con\(r_2\) tal que:
\[ \frac {r_1}{r_2} = \frac {(0.10^m)(0.050^n)}{(0.20^m)(0.050^n)} = \frac {3.05 \times 10^{-4}}{6.20 \times 10^{-4}} \]
\[ 0.5^m = 0.5 \]
\[ m = 1 \]
Podemos “tachar” la concentración de\([OCl^-]\) porque tiene la misma concentración en ambos ensayos utilizados.
Ahora que sabemos que m (\([I^-]\)) tiene un primer orden de 1.
No podemos “tachar”\([I^-]\) para encontrar\([OCl^-]\) porque no hay dos ensayos que tengan la misma concentración. Para resolver por n enchufaremos 1 para m.
\[ \frac {r_1}{r_3} = \frac {(0.10^{1})(0.050^n)}{(0.30^{1})(0.010^n)} = \frac {3.05 \times 10^{-4}}{1.83 \times 10^{-4}} \]
\[ \frac {1}{3} (5^{n}) = 1.6666667 \]
\[ 5^{n} = 5 \]
\[ n = 1 \]
Dado que sabemos que los órdenes tanto de n como de m son iguales a uno, no podemos sustituirlos en la ecuación de la ley de tasa junto con las concentraciones respectivas (ya sea de la primera, segunda o tercera reacción) y resolver para la constante de velocidad, k.
\[ r=k[OCl^-]^n[I^-]^m \]
\[ 3.05 * 10^{-4}= k[0.05]^1[0.10]^1 \]
\[ k = 6.1 * 10^{-2} \frac {L}{mol \times s} \]
Así, la ley general de tarifas es: $ r = (6.1 * 10^ {-2}\ frac {L} {mol\ times s}) [OCl^-] [I^-]\]
Las unidades para K dependen del orden general de la reacción. Para encontrar el orden general sumamos m y n juntos. Al hacer esto encontramos un orden general de 2. Es por esto que las unidades para K son $\ frac {L} {mol\ times s}\]
- Responder
-
tasa = k [I −] [OCl −1]; k = 6.1 × 10 −2 L mol −1 s −1
Q12.3.23
En la reacción
\[2NO + Cl_2 → 2NOCl\nonumber \]
los reactivos y productos son gases a la temperatura de la reacción. Se midieron los siguientes datos de velocidad para tres experimentos:
| Inicial p {NO} | Inicial p {Cl 2} | Tasa Inicial |
|---|---|---|
| (atm) | (atm) | (moles de A consumidos atm seg -1) |
| 0.50 | 0.50 | 5.1 x 10 -3 |
| 1.0 | 1.0 | 4.0 x 10 -2 |
| 0.50 | 1.0 | 1.0 x 10 -2 |
- A partir de estos datos, escriba la ecuación de velocidad para esta reacción gaseosa. ¿Cuál es el orden de reacción en NO, Cl 2 y en general?
- Calcular la constante de velocidad específica para esta reacción.
- Solución
-
a. La ecuación de velocidad se puede determinar diseñando experimentos que midan la (s) concentración (es) de uno o más reactivos o productos en función del tiempo. Para la reacción\(A+B\rightarrow products\), por ejemplo, necesitamos determinar k y los exponentes m y n en la siguiente ecuación:
\[rate=k[A]^m[B]^n\nonumber \]
Para ello, la concentración inicial de B puede mantenerse constante mientras se varía la concentración inicial de A y calcular la velocidad de reacción inicial. Esta información deduciría el orden de reacción con respecto a A. El mismo proceso se puede hacer para encontrar el orden de reacción con respecto a B.
En este ejemplo en particular,
\[\frac{rate_2}{rate_3}=\frac{k[A_2]^m[B_2]^n}{k[A_3]^m[B_3]^n}\nonumber \]
Así tomando los valores de la tabla,
\[\frac{4.0*10^{-2}}{1.0*10^{-2}}=\frac{k[1.0]^m[1.0]^n}{k[0.5]^m[1.0]^n}\nonumber \]
y al cancelar términos similares, te quedas con
\[\frac{4.0*10^{-2}}{1.0*10^{-2}}=\frac{[1.0]^m}{[0.5]^m}\nonumber \]
Ahora, resuelve para m
\(4=2^m\Longrightarrow m=2\) Porque m=2, la reacción con respecto a\(NO\) es 2. \(NO\)es de segundo orden.
Puedes repetir el mismo proceso para encontrar n.
\[\frac{rate_3}{rate_1}=\frac{k[A_3]^m[B_3]^n}{k[A_1]^m[B_1]^n}\nonumber \]
Tomando los valores de la tabla,
\[\frac{1.0*10^{-2}}{5.1*10^{-3}}=\frac{k[0.5]^m[1.0]^n}{k[0.5]^m[0.5]^n}\nonumber \]
y cancelando términos similares, te quedas con
\[\frac{1.0*10^{-2}}{5.1*10^{-3}}=\frac{[1.0]^n}{[0.5]^n}\nonumber \]
Ahora esta vez, resolver para n
\(2=2^n\Longrightarrow n=1\)
Porque n=1, la reacción con respecto a\(Cl_2\) es 1. \(Cl_2\)es de primer orden.
Entonces la ecuación de tasa es\[rate=k[NO]^2[Cl_2]^1\nonumber \]
Para encontrar el orden general de la tasa, simplemente suma los pedidos juntos. Segundo orden + primer orden hace que la reacción general sea de tercer orden.b. La constante de velocidad se calcula insertando los datos de cualquier fila de la tabla en la ley de velocidad determinada experimentalmente y resolviendo para k. Para una reacción de tercer orden, las unidades de k son\(frac{1}{atm^2*sec}\). Usando el Experimento 1,
\[rate=k[NO]^2[Cl_2]^1\Longrightarrow 5.1*10^{-3} \frac{atm}{sec}=k[0.5m atm]^2[0.5 atm]^1\nonumber \]
\[k=0.0408 \frac{1}{atm^2*sec}\nonumber \]
- Responder
-
\(NO\)es de segundo orden.
\(Cl_2\)es de primer orden.
El orden general de reacción es tres.
b)
\(k=0.0408\; atm^{-2}*sec^{-1}\)
12.4: Leyes de Tarifas Integradas
Q12.4.1
Describir cómo se pueden utilizar métodos gráficos para determinar el orden de una reacción y su constante de velocidad a partir de una serie de datos que incluyen la concentración de A en diferentes momentos.
- Solución
-
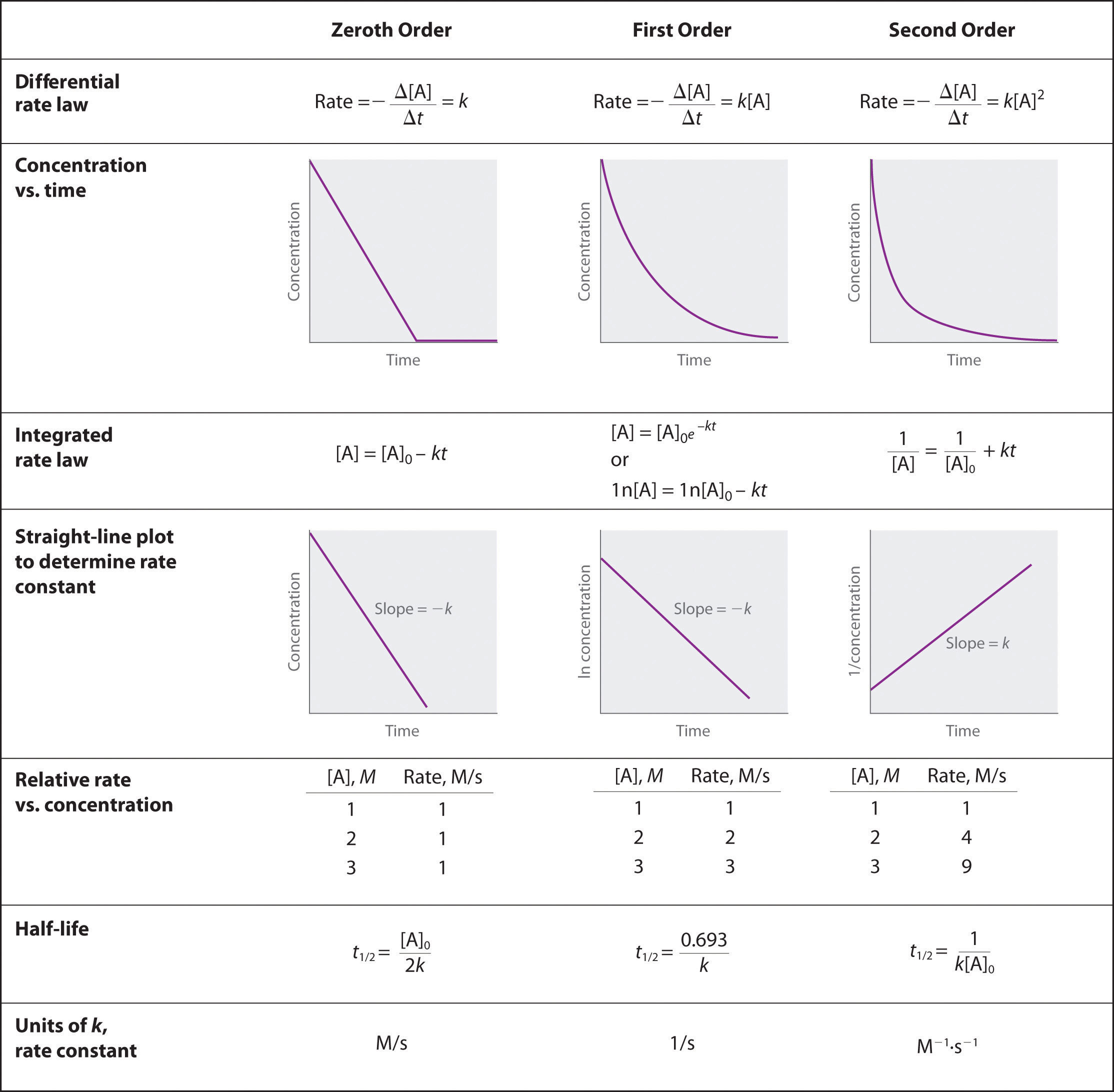
Para determinar el orden de una reacción cuando se le da la serie de datos, se deben graficar los datos como son, graficarlos como log natural de [A] y graficarlos como 1/ [A]. Cualquiera que sea el método que arroje una línea recta determinará el orden. Respectivamente de los métodos de graficar anteriores, si una línea recta es cedida por el primer método de graficación es un orden 0, si por el segundo método es un 1er orden, y el tercer método de graficación es un 2do orden. Cuando se conoce el orden de la gráfica, se puede utilizar una serie de ecuaciones, dadas en la imagen anterior, con los diversos puntos de la gráfica para determinar el valor de k, podemos ver que necesitamos un valor inicial de A y un valor final de A, y ambos estarían dados por los datos.
El orden cero al trazar la concentración inicial versus la concentración final tiene una pendiente lineal negativa.
\[[A] = [A]_0 − kt\nonumber \]
En primer orden al trazar ln [concentración inicial] versus ln [concentración final] se tiene una pendiente lineal negativa.
\[\ln[A] = \ln[A]_0 − kt\nonumber \]
Segundo orden al trazar el 1/ [concentración inicial] versus 1/ [concentración final] se tiene una pendiente lineal positiva.
\[\dfrac{1}{[\textrm A]}=\dfrac{1}{[\textrm A]_0}+kt\nonumber \]
Q12.4.2
Utilice los datos proporcionados para determinar gráficamente el orden y la constante de velocidad de la siguiente reacción:\(\ce{SO2Cl2 ⟶ SO2 + Cl2}\)
| Tiempo (s) | 0 | 5.00 × 10 3 | 1.00 × 10 4 | 1.50 × 10 4 | 2.50 × 10 4 | 3.00 × 10 4 | 4.00 × 10 4 |
|---|---|---|---|---|---|---|---|
| [SO 2 Cl 2] (M) | 0.100 | 0.0896 | 0.0802 | 0.0719 | 0.0577 | 0.0517 | 0.0415 |
- Solución
-
Utilice los datos para determinar gráficamente el orden y la constante de velocidad de la siguiente reacción.
Para determinar la ley de velocidad para una reacción a partir de un conjunto de datos consistentes en concentración (o los valores de alguna función de concentración) versus tiempo, haga tres gráficos de los datos basados en las leyes de velocidad integradas de cada reacción de orden.
[concentración] versus tiempo (lineal para una reacción de orden cero) ln [concentración] versus tiempo (lineal para una reacción de primer orden) 1/[concentración] versus tiempo (lineal para una reacción de orden 2)pendiente= -2.0 x 10 -5
k = 2.0 x 10 -5
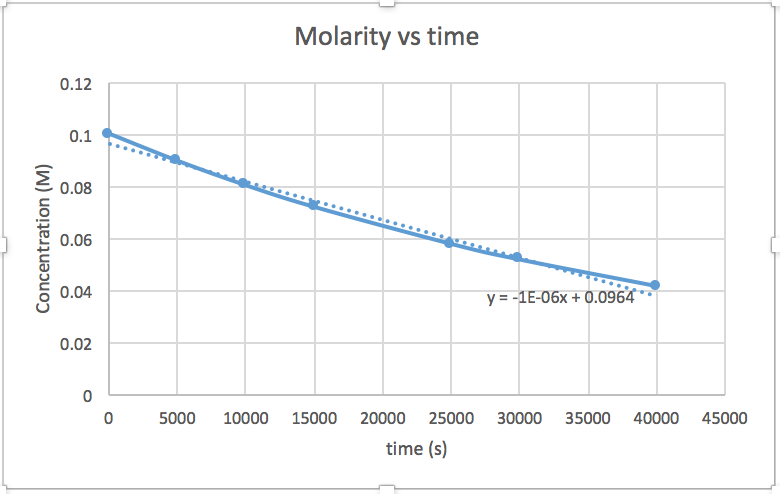
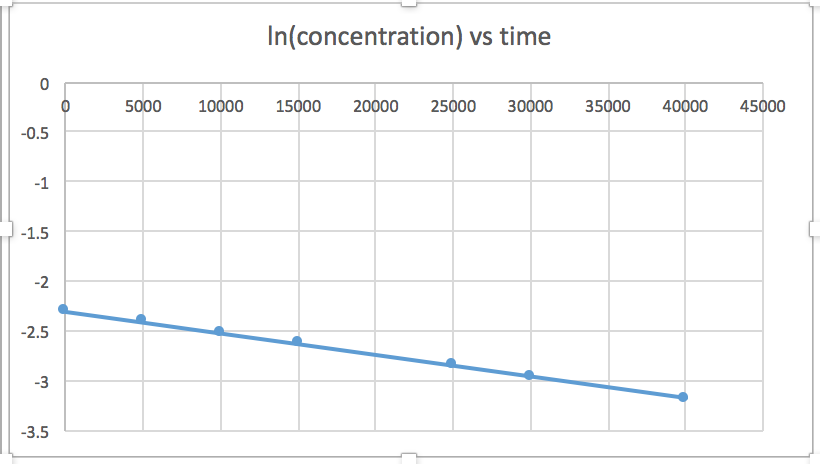
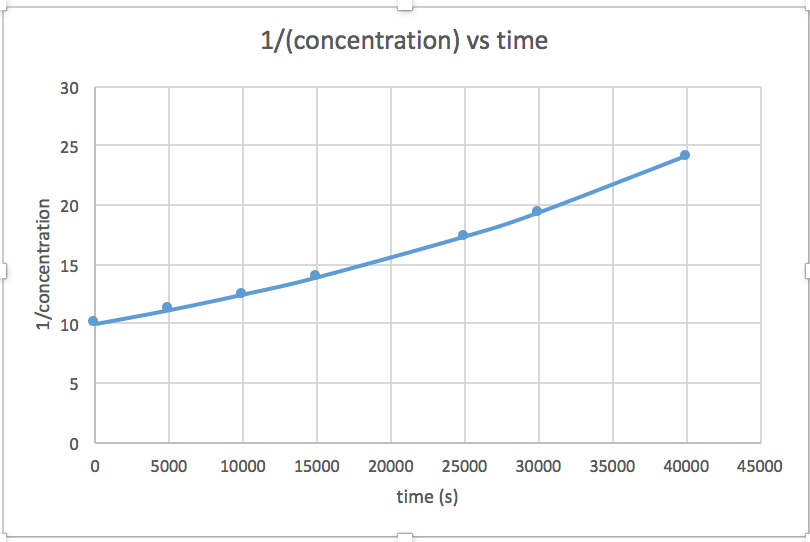
El gráfico que es lineal indica el orden de la reacción. Luego, puede encontrar la ecuación de tasa correcta:
reacción de orden cero tasa = k (k = - pendiente de línea) 1 reacción de orden tasa = k [A] (k = - pendiente de línea) Reacción de orden 2 tasa = k [A] 2 (k = pendiente de línea) En esta gráfica, ln (concentración) vs tiempo es lineal, lo que indica que la reacción es de primer orden.
k=-pendiente de línea
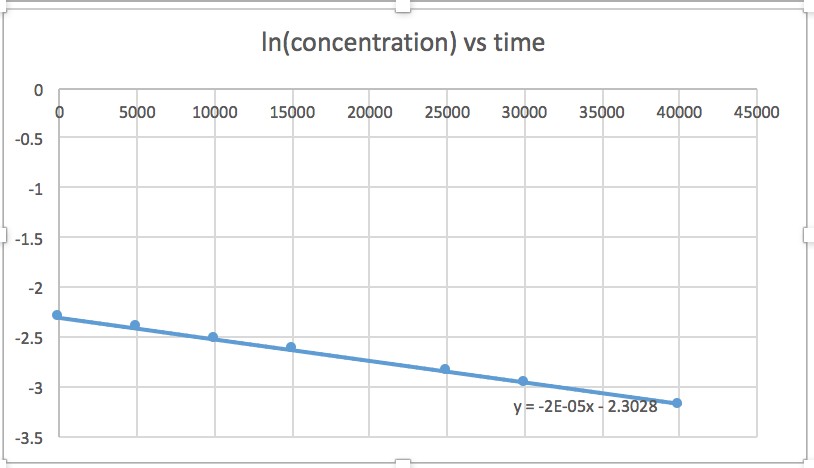
- Responder
-
Trazar una gráfica de ln [SO 2 Cl 2] versus t revela una tendencia lineal; por lo tanto, sabemos que esta es una reacción de primer orden:
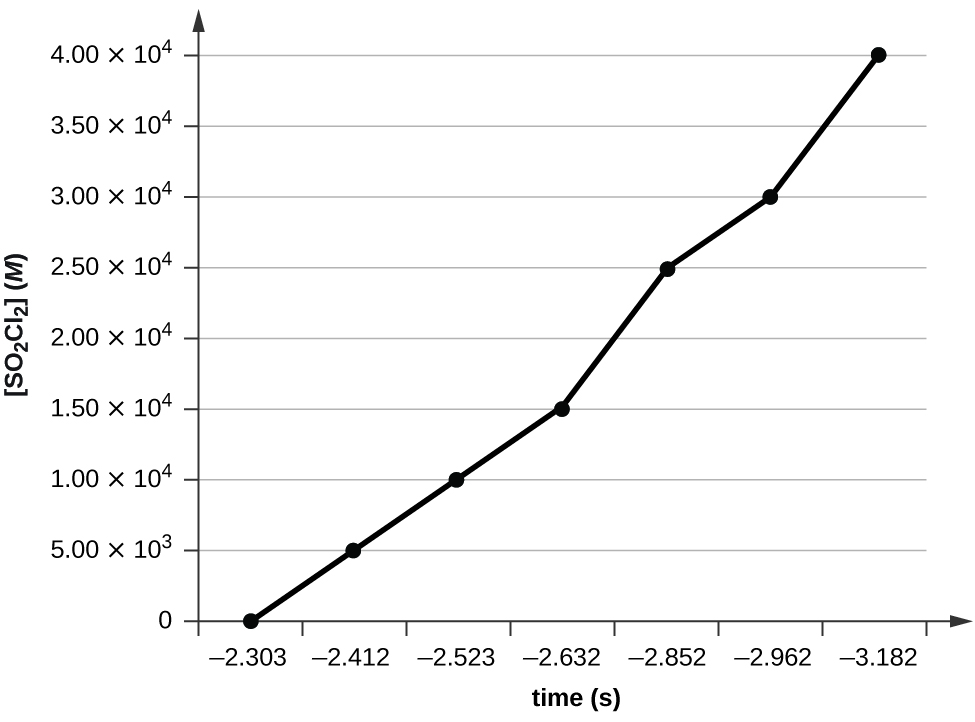
k = −2.20 × 10 5 s −1
Q12.4.3
Utilice los datos proporcionados en un método gráfico para determinar el orden y la constante de velocidad de la siguiente reacción:
\[2P⟶Q+W\nonumber \]
| Tiempo (s) | 9.0 | 13.0 | 18.0 | 22.0 | 25.0 |
|---|---|---|---|---|---|
| [P] (M) | 1.077 × 10 −3 | 1.068 × 10 −3 | 1.055 × 10 −3 | 1.046 × 10 −3 | 1.039 × 10 −3 |
- Solución
-
Agrega textos aquí. No borre primero este texto.
Q12.4.4
El ozono puro se descompone lentamente a oxígeno,\(\ce{2O3}(g)⟶\ce{3O2}(g)\). Utilizar los datos proporcionados en un método gráfico y determinar el orden y la constante de velocidad de la reacción.
| Tiempo (h) | 0 | 2.0 × 10 3 | 7.6 × 10 3 | 1.23 × 10 4 | 1.70 × 10 4 | 1.70 × 10 4 |
|---|---|---|---|---|---|---|
| [O 3] (M) | 1.00 × 10 −5 | 4.98 × 10 −6 | 2.07 × 10 −6 | 1.39 × 10 −6 | 1.22 × 10 −6 | 1.05 × 10 −6 |
- Solución
-
Para determinar el orden y la constante de velocidad, es necesario graficar los datos para orden cero, primer orden y segundo orden trazando concentración versus tiempo- [A] vs tiempo, logaritmo natural (ln) de [A] vs tiempo, y 1/ [A] vs tiempo respectivamente. El orden de la reacción se determina identificando cuál de estas tres gráficas produce una línea recta. La constante de velocidad k está representada por la pendiente de la gráfica. Las gráficas con sus respectivos valores de datos serían
Tiempo (s) 9.0 13.0 18.0 22.0 25.0 [P] (M) 1.077 × 10−3 1.068 × 10−3 1.055 × 10−3 1.046 × 10−3 1.039 × 10−3 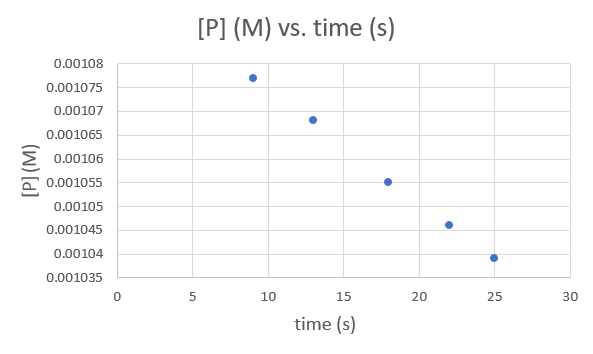.png)
Tiempo (s) 9.0 13.0 18.0 22.0 25.0 ln [P] (M) -6.83358 -6.84197 -6.85421 -6.86278 -6.8695 .png)
Tiempo (s) 9.0 13.0 18.0 22.0 25.0 1/ [P] (M) 928.5051 936.3296 947.8673 956.0229 962.4639 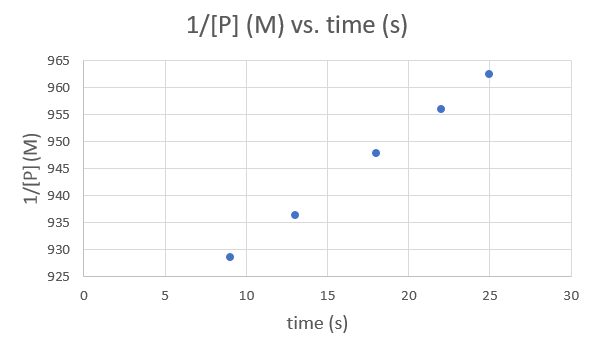.png)
Dado que cada gráfico produce una línea recta, no se puede determinar el orden y la constante de velocidad de la reacción.
Identificar cómo las concentraciones cambian una función del tiempo, requiere resolver la ecuación diferencial apropiada (es decir, la ley de tasa diferencial).
La ley de tasa de orden cero predice en una disminución lineal de la concentración con
el tiempo La ley de tasa de primer orden predice en una disminución exponencial de la concentración con
el tiempo La ley de tasa de segundo orden predice en una disminución recíproca de la concentración con el tiempo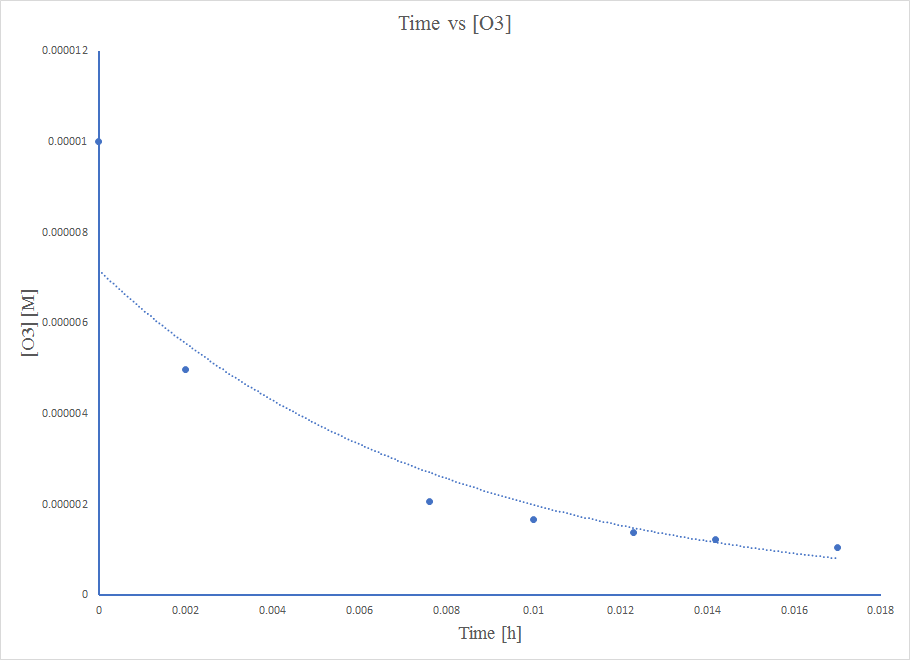
La gráfica no es lineal, por lo que la reacción no es de orden cero.

La trama no es lineal, por lo que la reacción no es de primer orden.
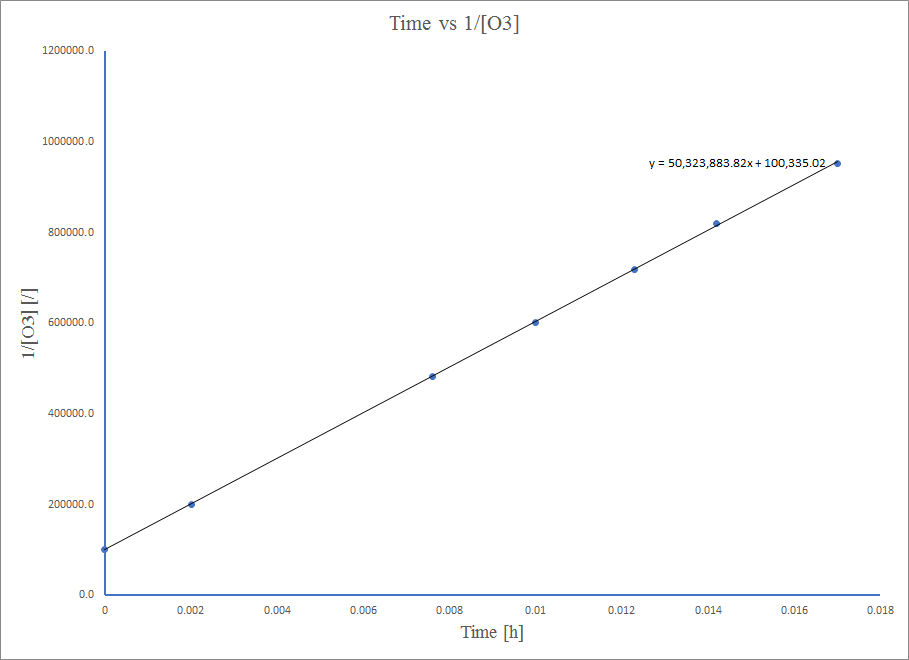
La trama es muy lineal, por lo que la reacción es de segundo orden.
A una ecuación de segundo orden,\( 1/[A] \ = k*t + 1/[A_0] \)
Así, el valor de K es la pendiente de la gráfica Tiempo vs\( \frac{1}{\ce{O3}}\),
k = 50.3*10^6 L mol −1 h −1
- Responder
-
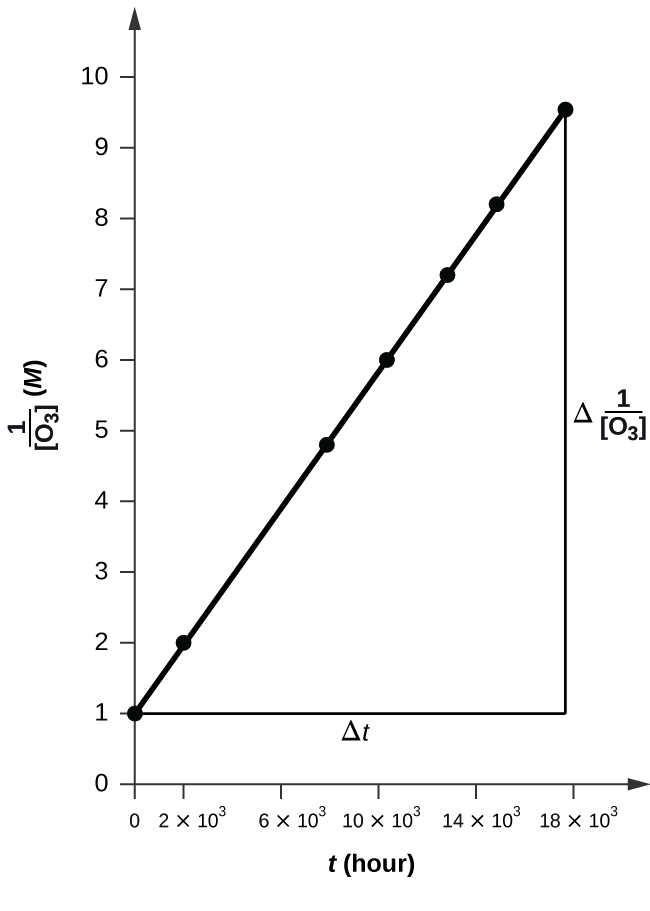
La trama es muy lineal, por lo que la reacción es de segundo orden.
k = 50,1 L mol −1 h −1
Q12.4.5
A partir de los datos dados, utilice un método gráfico para determinar el orden y la constante de velocidad de la siguiente reacción:
\[2X⟶Y+Z\]
| Tiempo (s) | 5.0 | 10.0 | 15.0 | 20.0 | 25.0 | 30.0 | 35.0 | 40.0 |
|---|---|---|---|---|---|---|---|---|
| [X] (M) | 0.0990 | 0.0497 | 0.0332 | 0.0249 | 0.0200 | 0.0166 | 0.0143 | 0.0125 |
- Solución
-
Para determinar el orden de la reacción necesitamos trazar los datos utilizando tres gráficas diferentes. Las tres gráficas tendrán tiempo en segundos como eje x, pero el eje y es lo que diferirá. Una gráfica representará la concentración versus el tiempo, la segunda representará el log natural de concentración versus el tiempo y la otra representará 1/concentración versus tiempos. Cualquiera que sea el gráfico que resulte en una línea, sabemos que ese debe ser el orden de la reacción. Si obtenemos una línea usando la primera gráfica, será de orden cero, si es una línea para la segunda gráfica será de primer orden, y si es una línea para la tercera gráfica será una reacción de segundo orden. Ahora vamos a trazar los datos para determinar el orden.



Podemos ver claramente que la tercera gráfica, que traza 1/M versus tiempo, es una línea recta mientras que las otras dos están ligeramente curvadas. Por lo tanto, podemos determinar que la velocidad de esta reacción es de segundo orden. Esto también nos dice que las unidades de la constante de velocidad que deben ser M -2 s -1 para una reacción de segundo orden.
Para determinar la constante de velocidad, llamada k, simplemente necesitamos averiguar la pendiente de la tercera gráfica ya que ese es el orden de esta reacción. Para encontrar la pendiente de la línea, tomamos dos puntos y restamos los valores y y luego los dividimos por la diferencia de los valores x. Así es como hacerlo:
Utilice los puntos (5, 10.101) y (40, 80).
Ahora usa estos para obtener el slop, también conocido como la constante de velocidad: (80-10.101)/(40-5) = 1.997 = k
Por lo que la constante de velocidad para esta reacción de segundo orden es de 1.997 M -1 s -1.
Q12.4.6
¿Cuál es la vida media para la descomposición de primer orden del fósforo-32? \(\ce{(^{32}_{15}P⟶^{32}_{16}S + e- )}\)La constante de velocidad para el decaimiento es de 4.85 × 10 −2 días −1.
- Solución
-
Esta es una reacción de primer orden, por lo que podemos usar nuestra ecuación de vida media a continuación:
\[t_{1/2}=\frac{0.693}{k}\nonumber \]
La constante de tarifa se nos da en unidades por día. Todo lo que tenemos que hacer, es enchufarlo a la ecuación.
\[t_{1/2}=\frac{0.693}{4.85*10^{-2}}\nonumber \]
\[=14.3\; days\nonumber \]A12.4.6
14.3 d
Q12.4.7
¿Cuál es la vida media para la desintegración de primer orden del carbono-14? \(\ce{(^6_{14}C⟶^7_{14}N + e- )}\)La constante de tasa para el decaimiento es 1.21 × 10 −4 año −1.
- Solución
-
Para encontrar la semivida, necesitamos usar la ecuación de semivida de primer orden. Todas las reacciones de vida media experimentan reacciones de primer orden.
La ecuación de semivida para primer orden es\[t_{1/2}=ln2/k \nonumber \] con k siendo la constante de velocidad. La constante de velocidad para carbono-14 se dio como\(1.21 × 10^{-4} year^{−1}\).
Enchufarlo en la ecuación. \[t_{1/2}=ln2/(1.21 × 10^{−4} year^{−1})\nonumber \]y resolver para\( t_{1/2}\).
Al calcularlo, la vida media para el carbono-14 es 5.73*10 3
- Responder
-
La vida media para el carbono-14 se calcula para ser 5.73*10 3
Q12.4.8
¿Cuál es la vida media para la descomposición de NOCl cuando la concentración de NOCl es 0.15 M? La constante de velocidad para esta reacción de segundo orden es de 8.0 × 10 −8 L/mol/s.
- Solución
-
La vida media de una reacción, t 1/2, es la cantidad de tiempo que se requiere para que la concentración de un reactivo disminuya a la mitad en comparación con su concentración inicial. Al resolver la vida media de una reacción, primero debemos considerar el orden de reacción para determinar su ley de velocidad. En este caso, se nos dice que esta reacción es de segundo orden, por lo que sabemos que la ley de tasa integrada se da como:
\[\dfrac{1}{[A]} = kt + \dfrac{1}{[A]_0}\nonumber \]
Aislado por el tiempo, encontramos que:
\[t_{1/2} = \dfrac{1}{k[A]_0}\nonumber \]
Ahora solo se trata de sustituir la información que nos han dado para calcular\(t_{1/2}\), donde la constante de velocidad,\({k}\), es igual a 8.0 × 10 −8 L/mol/s y la concentración inicial,\({[A]_0}\), es igual a 0.15 M:
\[t_{1/2} = \dfrac{1}{(8.0×10^{-8})(0.15)} = {8.33×10^7 seconds}\nonumber \]
- Contestar
-
8.33 × 10 7 s
Q12.4.9
¿Cuál es la vida media para la descomposición de O 3 cuando la concentración de O 3 es 2.35 × 10 −6 M? La constante de velocidad para esta reacción de segundo orden es de 50.4 L/mol/h.
- Solución
-
Agrega textos aquí. No borre primero este texto.
Dado que la reacción es de segundo orden, su vida media es
\[t_{1/2}=\dfrac{1}{(50.4M^{-1}/h)[2.35×10^{-6}M]}\nonumber \]
Entonces, la vida media es de 8443 horas.
Q12.4.10
La reacción del compuesto A para dar los compuestos C y D se encontró que era de segundo orden en A. Se determinó que la constante de velocidad para la reacción era de 2.42 L/mol/s Si la concentración inicial es de 0.500 mol/L, ¿cuál es el valor de t 1/2?
- Solución
-
Como se mencionó en la pregunta la reacción del compuesto A dará como resultado la formación de los compuestos C y D. Esta reacción se encontró que era de segundo orden en A. Por lo tanto, debemos usar la ecuación de segundo orden para la vida media que relaciona la constante de velocidad y las concentraciones iniciales con la vida media:
\[t_{\frac{1}{2}}=\frac{1}{k[A]_{0}}\nonumber \]
Desde que nos dieron k (constante de tasa) y concentración inicial de A, tenemos todo lo necesario para calcular la semivida de A.
\[k=0.5\frac{\frac{L}{mol}}{s}\nonumber \]
\[[A]_{0}=2.42\frac{mol}{L}\nonumber \]
Cuando enchufamos la información dada avisamos de que las unidades cancelan a segundos.
\[t_{\frac{1}{2}}=\frac{1}{\frac{2.42Lmol^{-}}{s}[0.500\frac{mol}{L}]}=0.826 s\nonumber \]
- Responder
-
0.826 s
Q12.4.11
La semivida de una reacción del compuesto A para dar los compuestos D y E es de 8.50 minutos cuando la concentración inicial de A es de 0.150 mol/L. ¿Cuánto tiempo tomará para que la concentración baje a 0.0300 mol/L si la reacción es (a) de primer orden con respecto a A o b) segundo orden con respecto a A?
- Solución
-
Organizar las variables dadas:
(semivida de A)\(t_{1/2}=8.50min\)
(concentración inicial de A)\([A]_{0}=0.150mol/L\)
(concentración objetivo de A)\([A]=0.0300mol/L\)Encuentra la constante de velocidad k, usando las fórmulas de vida media para cada orden respectivo. Después de encontrar k, use la ley de tasa integrada respectiva a cada orden y las concentraciones inicial y objetivo de A para encontrar el tiempo que tardó en bajar la concentración.
(a) primer orden con respecto a A
(vida media)\(t_{1/2}=\frac{ln(2)}{k}=\frac{0.693}{k}\)
(reorganizado para k)\(k=\frac{0.693}{t_{1/2}}\)
(plug in t 1/2 = 8.50 min)\(k=\frac{0.693}{8.50min}=0.0815min^{-1}\)(ley de tasa integrada)\(ln[A]=-kt+ln[A]_{0}\)
(reorganizado para t)\(ln(\frac{[A]}{[A]_{0}})=-kt\)
\(-ln(\frac{[A]}{[A]_{0}})=kt\)
\(ln(\frac{[A]}{[A]_{0}})^{-1}=kt\)
\(ln(\frac{[A]_{0}}{[A]})=kt\)
\(t=\frac{ln(\frac{[A]_{0}}{[A]})}{k}\)
(variables enchufables)\(t=\frac{ln(\frac{0.150mol/L}{0.0300mol/L})}{0.0815min^{-1}}=\frac{ln(5.00)}{0.0815min^{-1}}=19.7min\)b) segundo orden con respecto a A
(vida media)\(t_{1/2}=\frac{1}{k[A]_{0}}\)
(reorganizado para k)\(k=\frac{1}{t_{1/2}[A]_{0}}\)
(variables enchufables)\(k=\frac{1}{(8.50min)(0.150mol/L)}=\frac{1}{1.275min\cdot mol/L}=0.784L/mol\cdot min\)(ley de tasa integrada)\(\frac{1}{[A]}=kt+\frac{1}{[A]_{0}}\)
(reorganizado para t)\(\frac{1}{[A]}-\frac{1}{[A]_{0}}=kt\)
\(t=\frac{1}{k}(\frac{1}{[A]}-\frac{1}{[A]_{0}})\)
(variables enchufables)\(t=\frac{1}{0.784L/mol\cdot min}(\frac{1}{0.0300mol/L}-\frac{1}{0.150mol/L})=\frac{1}{0.784L/mol\cdot min}(\frac{80}{3}L/mol)=34.0min\)
- Responder
-
a) 19.7 min
b) 34,0 min
Q12.4.12
Algunas bacterias son resistentes al antibiótico penicilina porque producen penicilinasa, una enzima con un peso molecular de 3 × 10 4 g/mol que convierte la penicilina en moléculas inactivas. Aunque la cinética de las reacciones catalizadas por enzimas puede ser compleja, a bajas concentraciones esta reacción puede describirse mediante una ecuación de velocidad que es de primer orden en el catalizador (penicilinasa) y que también implica la concentración de penicilina. A partir de los siguientes datos: 1.0 L de una solución que contiene 0.15 µg (0.15 × 10 −6 g) de penicilinasa, determinar el orden de la reacción con respecto a la penicilina y el valor de la constante de velocidad.
| [Penicilina] (M) | Tasa (mol/L/min) |
|---|---|
| 2.0 × 10 −6 | 1.0 × 10 −10 |
| 3.0 × 10 −6 | 1.5 × 10 −10 |
| 4.0 × 10 −6 | 2.0 × 10 −10 |
- Solución
-
El primer paso es resolver por el orden o la reacción. Esto se puede hacer estableciendo dos expresiones que equiparen la velocidad a la constante de velocidad por la concentración molar de penicilina elevada a la potencia de su orden. Una vez que tenemos ambas expresiones establecidas, podemos dividirlas para cancelar k (constante de velocidad) y usar un logaritmo básico para resolver para el exponente, que es el orden. Se verá así.
tasa (mol/l/min) =k [M] x
(1.0 x 10 -10) =k [2.0 x 10 -6] x
(1.5 x 10 -10) =k [3.0 x 10 -6] x
Dividir las dos ecuaciones da como resultado la expresión:
(2/3) = (2/3) x
*También se puede configurar una ecuación de relación única para resolver el orden de reacción:
*\[\frac{rate_{1}}{rate_{2}}=\frac{k[Penicillin]_{1}^{x}}{k[Penicillin]_{2}^{x}}\nonumber \]
*Luego resolvemos para x de manera similar.
*\[\frac{1.0x10^{-10}}{1.5x10^{-10}}=\frac{[2.0x10^{-6}]^{x}}{[3.0x10^{-6}]^{x}}\nonumber \]
Ahora podemos usar el logaritmo natural para resolver para x, o simple e intuitivamente ver que para que la ecuación funcione, x debe ser igual a uno. Así, la reacción es de primer orden.
Ahora que tenemos el orden de la reacción, podemos proceder a resolver por el valor de la constante de velocidad. Sustituyendo x=1 en nuestra primera ecuación produce la expresión:(1 x 10 -10) =k [2.0 x 10 -6] 1
k= (1 x 10 -10)/(2 x 10 -6)
k= (5 x 10 -5) min -1
Tenemos una unidad de min -1 porque dividimos (mol/L/min) por molaridad, que está en (mol/L), produciendo una unidad de min -1.
Nos dieron dos importantes piezas de información para terminar con el problema. Se afirma que la enzima tiene un peso molecular de 3 × 10 4 g/mol, y que tenemos una solución de un litro que contiene (0.15 x 10 -6 g) de penicilinasa. Al dividir la cantidad de gramos por el peso molecular se obtienen 5 x 10 -12 moles.
(0.15 x 10 -6) g/(3 x 10 4) g/mol = (5 x 10 -12) mol
Ahora que tenemos la cantidad de moles, podemos dividir nuestra constante de tasa por este valor.
(5 x 10 -5) min -1/(5 x 10 -12) mol = (1 x 10 7) mol -1 min -1
Responder
-
La reacción es de primer orden con k = 1.0 × 10 7 mol -1 min -1
Q12.4.13
Tanto el tecnecio-99 como el talio-201 se utilizan para obtener imágenes del músculo cardíaco en pacientes con sospecha de problemas cardíacos. Las vidas medias son de 6 h y 73 h, respectivamente. ¿Qué porcentaje de radiactividad quedaría para cada uno de los isótopos después de 2 días (48 h)?
- Solución
-
Este problema nos está pidiendo el porcentaje de radiactividad restante después de cierto tiempo para ambos isótopos después de 48 horas. Debemos identificar una ecuación que nos ayude a resolver esto y podemos determinar que podemos determinar esta información usando la ecuación de primer orden.
Esta ecuación Ln (N/N o) = -kt indica que el logaritmo Natural de la fracción restante es igual a la constante de velocidad por tiempo. Para determinar la constante de velocidad, también podemos calcular .693 a lo largo de la vida media dada en la información.
Para Tecnecio-99 podemos determinar la constante de velocidad conectándonos a la segunda ecuación: .693/6 hrs= .1155 h -1
Ahora que tenemos la constante de velocidad podemos enchufar: Ln (N/N o) =- (.1155h -1) (48h) así Ln (N/N o) =-5.544 y si tomamos la inversa del logaritmo natural, obtenemos (N/N o) =3.9x10 -3 y si multiplicamos esto por 100, obtenemos .39% restante.
Podemos hacer este mismo proceso para Tallio-201 y plugin: .693/73 hrs= .009493151 h -1 y cuando conectamos esto a la ecuación de primer orden obtenemos:
Ln (N/N o) =- (.009493h -1) (48h) entonces Ln (N/N o) =-.45567248 y cuando tomamos la inversa del logaritmo natural, obtenemos (N/N o) =.6340 y cuando se multiplica por 100, obtenemos 63.40% restante lo cual tiene sentido ya que su vida media es de 73 horas y solo han pasado 48 horas, la mitad de la cantidad aún no se ha consumido.
- Responder
-
Tecnecio-99:0.39%
Talio-201:63.40%
Q12.4.14
Hay dos moléculas con la fórmula C 3 H 6. El propeno\(\ce{CH_3CH=CH_2}\), es el monómero del polipropileno polimérico, que se utiliza para alfombras interior-exterior. El ciclopropano se utiliza como anestésico:

Cuando se calienta a 499 °C, el ciclopropano se reorganiza (isomeriza) y forma propeno con una constante de velocidad de 5.95 × 10 −4 s −1. ¿Cuál es la vida media de esta reacción? ¿Qué fracción del ciclopropano queda después de 0.75 h a 499 °C?
- Solución
-
Usa la ecuación\[ t{_1}{_/}{_2} = \frac{ln2} k\nonumber \] ya que esta es una reacción de primer orden. Se puede decir que esta es una reacción de primer orden debido a las unidades de medida de la constante de velocidad, que es s -1. Diferentes órdenes de reacciones conducen a diferentes constantes de velocidad, y una constante de velocidad de s -1 siempre será de primer orden.
Enchufe en la ecuación, y obtendrá la semivida = 1164.95 segundos. Para convertir esto en horas, dividiríamos este número por 3600 segundos/hora, para obtener 0.324 horas.
Utilice la ley de tasa integrada de primer orden\[ln\frac{[A]}{[A]_0} = -kt\nonumber \]. En esta ecuación, [A] 0 representa la cantidad inicial de compuesto presente en el tiempo 0, mientras que [A] representa la cantidad de compuesto que queda después de que se haya producido la reacción. Por lo tanto, la fracción\[\frac{[A]}{[A]_0}\nonumber \] es igual a la fracción de ciclopropano que queda después de cierto tiempo, en este caso, 0.75 horas.
Sustituir x por la fracción de\[\frac{[A]}{[A]_0}\nonumber \] en la ley de tasa integrada:\[ln\frac{[A]}{[A]_0} = -kt\nonumber \]\[ln(x) = -5.95x10^{-4}(0.75)\nonumber \]\[x=e^{(-0.000595)(0.75)}\nonumber \] = 0.20058 = 20%.
Entonces, la semivida es de 0.324 horas, y el 20% del ciclopropano permanecerá ya que 80% habrá formado propeno.
- Responder
-
0.324 horas.; 20% permanece
Q12.4.16
Fluorine-18 es un isótopo radiactivo que se desintegra por emisión de positrones para formar oxígeno-18 con una vida media de 109.7 min. (Un positrón es una partícula con la masa de un electrón y una sola unidad de carga positiva; la ecuación nuclear es\(\ce{^{18}_9F ⟶ _8^{18}O + ^0_{1}e^+}\).) Los médicos usan 18 F para estudiar el cerebro inyectando una cantidad de glucosa fluoro-sustituida en la sangre de un paciente. La glucosa se acumula en las regiones donde el cerebro está activo y necesita nutrición.
- ¿Cuál es la constante de velocidad para la descomposición del fluor-18?
- Si se inyecta en la sangre una muestra de glucosa que contiene fluor-18 radiactivo, ¿qué porcentaje de la radiactividad quedará después de 5.59 h?
- ¿Cuánto tiempo tarda en decairse el 99.99% de los 18 F?
- Solución
-
a) La desintegración nuclear de un isótopo de un elemento está representada por la ecuación de primer orden:
ln (N/N0) = −kt
Donde t es tiempo, N0 es la cantidad inicial de la sustancia, N es la cantidad de la sustancia después del tiempo t, y k es la constante de velocidad. Podemos reorganizar la ecuación y aislar k para que podamos resolver para la constante de velocidad:
k = [-ln (N/N0)]/t
Se nos da que el fluor-18 tiene una vida media de 109.7 minutos. Como tenemos la vida media, podemos elegir un valor arbitrario para N 0 y usar la mitad de ese valor para N. En este caso, elegimos 100 para N 0 y 50 para N. Ahora podemos enchufar esos valores en la ecuación anterior y resolver para k.
k = [-ln (50/100)]/109.7
k = 0.6931/109.7 = 0.006319 min -1
La constante de velocidad para esta reacción es 0.006319 min -1.
b) Para este problema, podemos usar la misma ecuación de la parte a:
ln (N/N0) = −kt
Sin embargo, esta vez se nos da la cantidad de tiempo transcurrido en lugar de la vida media, y se nos pide determinar el porcentaje de radiactividad fluor-18 restante después de ese tiempo. En este problema, debemos enchufar valores para N0, k (determinado a partir de la parte a) y t.
Pero primero, ya que se nos da el tiempo transcurrido en horas, debemos convertirlo en minutos:
5.59 horas x (60 minutos/1 horas) = 335.4 minutos
Esto nos da el valor para t También tenemos valores para k (0.006319 min -1) y N 0 (nuevamente un número arbitrario). Ahora podemos enchufar valores en la ecuación original, dándonos:
ln (N/100) = − (0.006319) (335.4)
Resolvemos esta ecuación tomando el exponencial de ambos lados:
e ln (N/100) = e − (0.006319) (335.4)
donde e ln es igual a 1 y ahora solo podemos resolver para N:
N/100 = e − (0.006319) (335.4)
N = [e − (0.006319) (335.4)] x 100 = 12.0
Ya que se utilizó 100 como cantidad inicial y se determinó 12.0 como la cantidad restante, 12.0 se puede utilizar como porcentaje de cantidad restante de radiactividad de fluor-18. Por lo tanto, el porcentaje de radiactividad fluorina-18 restante después de 5.59 horas es de 12.0%.
c) Esta parte de la pregunta es muy parecida a las dos partes anteriores, pero esta vez se nos da la cantidad inicial de radiactividad, la cantidad final de radiactividad y se nos pide que determinemos cuánto tiempo tardó en decairse esa cantidad de radiactividad. Somos capaces de usar la misma ecuación:
ln (N/N0) = −kt
No obstante, ahora se nos da N y N 0 y ya hemos determinado k de antes. Se nos dice que el 99.99% de la radiactividad ha decaído, por lo que podemos usar 100 y 0.01 para N 0 y N respectivamente. Conectamos estos valores a la ecuación, resolvemos para t y obtenemos
ln (0.01/1000) = −0.006319t
-9.21 = −0.006319t
t = 1458 minutos
Por lo tanto, tarda 1458 minutos para que el 99.99% de la radiactividad se descomponga.
- Responder
-
a) 0.006319 min -1
b) 12.0%
c) 1458 minutos
Q12.4.17
Supongamos que la vida media de los esteroides que toma un deportista es de 42 días. Suponiendo que los esteroides se biodegradan por un proceso de primer orden, ¿cuánto tiempo tardaría\(\dfrac{1}{64}\) de la dosis inicial en permanecer en el cuerpo del atleta?
- Solución
-
252 días
para reacción de primer orden: t 1/2 = 0.693/k
k = 0.693/42
k = 0.0165
para reacción de primer orden: [A] = [A] 0 e -kt
1/64 inicial significa que: [A] = 1/64 [A] 0
por lo tanto: 1/64 [A] 0 = [A] 0 e -0.0165t
t = 252 días
Q12.4.18
Recientemente, el esqueleto del rey Ricardo III fue encontrado debajo de un estacionamiento en Inglaterra. Si las muestras de tejido del esqueleto contienen alrededor del 93.79% del carbono-14 esperado en el tejido vivo, ¿en qué año murió el rey Ricardo III? La vida media para el carbono-14 es de 5730 años.
- Solución
-
Para saber en qué año murió el rey Ricardo III, establecer [A]/[A 0] (el porcentaje de carbono-14 aún contenido) igual a 0.5 tiempo (t) /vida media (t 1/2) o usar la ecuación N (t) = N 0 e -rt.
Usando la primera ecuación:
\(A/A_{0}\)=\(0.5^{t/t_{1/2}}\) enchufar los números dados\(.9379 = 0.5^{t/5730}\) y resolver para t.
\(ln.9379\)=\((t/5730)(ln0.5)\) (usando la regla de registros)
\(-.0641\)=\((t/5730)(-.693)\)
\(-367.36\)=\(-.693t\)
\(t = 530.1 years\)
El uso de\(N(t) = N_{0}e^{-rt}\) este problema se resuelve por lo siguiente:
\(1/2 = e^{-5730r}\)
\(r = 0.000121\)
Ahora que sabemos lo que es r, podemos usar este valor en nuestra fórmula original y resolver para t, la cantidad de años que han pasado.
Esta vez, usamos 93.78, el porcentaje del carbono-14 restante como N (t) y 100 como el original, N 0.
\(93.78 = 100e^{-0.000121t}\)
\(t = 530.7\)años
Otra forma de hacerlo es usando estas dos ecuaciones:
λ =\(\dfrac{0.693}{t_{1/2}}\) y\(\dfrac{n_{t}}{n_{0}}\) = -λt
\(n_{t}\)= concentración en el tiempo t (93.79)
\(n_{0}\)= concentración inicial (100)
Primero resuelve para lambda o la constante de decaimiento enchufando la semivida.
Luego, conecte lambda y los otros números en la segunda ecuación, y resuelva para t- que también debería ser igual a 530.1 años.
Si queremos saber en qué año murió el rey Ricardo III, tomamos el año en curso, 2017, y restamos 530 años. Haciendo esto, encontramos que el rey Ricardo III murió en el año 1487.
- Responder
-
Rey Ricardo III murió en el año 1487
Q12.4.19
La nitroglicerina es un explosivo extremadamente sensible. En una serie de experimentos cuidadosamente controlados, las muestras del explosivo se calentaron a 160 °C y se estudió su descomposición de primer orden. Determine las constantes de velocidad promedio para cada experimento utilizando los siguientes datos:
| Inicial [C 3 H 5 N 3 O 9] (M) | 4.88 | 3.52 | 2.29 | 1.81 | 5.33 | 4.05 | 2.95 | 1.72 |
|---|---|---|---|---|---|---|---|---|
| t (s) | 300 | 300 | 300 | 300 | 180 | 180 | 180 | 180 |
| % Descompuesto | 52.0 | 52.9 | 53.2 | 53.9 | 34.6 | 35.9 | 36.0 | 35.4 |
- Solución
-
Primero tenemos que entender qué es lo que se plantea la pregunta: la constante de tasa promedio. La constante de velocidad promedio es la variable “k” cuando se discute la cinética y puede definirse como la constante de proporcionalidad en la ecuación que expresa la relación entre la velocidad de una reacción química y las concentraciones de las sustancias reaccionantes. Sabiendo que necesitamos encontrar K en esta reacción de primer orden, podemos buscar fórmulas que incluyan “k”, concentraciones iniciales y finales\([A]_o and [A]_t\), y tiempo de vida media “t”. Como esta es una reacción de primer orden, podemos mirar a las ecuaciones de primer orden, y haciendo eso encontramos una que incluye las variables dadas en la pregunta:\[\ln[A]_t=-kt+\ln[A]_o\nonumber \]
Para la primera reacción, tenemos una concentración inicial de 4.88 M, y un porcentaje descompuesto. Para encontrar la concentración final, debemos multiplicar la concentración inicial por el porcentaje descompuesto para saber cuánto se descompone, y restarlo del original para averiguar cuánto queda: 4.88M x 0.52= 2.54 M y 4.88M-2.54M=2.34M
Ahora, tenemos las variables que necesitamos, y lo conectamos a la ecuación anterior:
\(\ln[A]_t=-kt+\ln[A]_o\)
\(\ln[2.34M]=-k(300s)+\ln[4.88M]\)
k=\({-(\ln[2.34M]-\ln[4.88M])}\over 300\)
\(k=2.45x10^{-3}\)
Dado que pide la constante de velocidad de cada experimento, ahora debemos hacer el mismo procedimiento para cada conjunto de datos para encontrar la constante de velocidad:
Segundo experimento
\(\ln[A]_t=-kt+\ln[A]_o\)
\(\ln[1.66M]=-k(300s)+\ln[3.52M]\)
k=\({-(\ln[1.66M]-\ln[3.52M])}\over 300\)
\(k=2.51x10^{-3}\)
Tercer experimento
\(\ln[A]_t=-kt+\ln[A]_o\)
\(\ln[1.07M]=-k(300s)+\ln[2.29M]\)
k=\({-(\ln[1.07M]-\ln[2.29M])}\over 300\)
\(k=2.54x10^{-3}\)
Cuarto experimento
\(\ln[A]_t=-kt+\ln[A]_o\)
\(\ln[0.834M]=-k(300s)+\ln[1.81M]\)
k=\({-(\ln[0.834M]-\ln[1.81M])}\over 300\)
\(k=2.58x10^{-3}\)
Quinto Experimento
\(\ln[A]_t=-kt+\ln[A]_o\)
\(\ln[3.49M]=-k(180s)+\ln[5.33M]\)
k=\({-(\ln[3.49M]-\ln[5.33M])}\over 180\)
\(k=2.35x10^{-3}\)
Sexto Experimento
\(\ln[A]_t=-kt+\ln[A]_o\)
\(\ln[2.60M]=-k(180s)+\ln[4.05M]\)
k=\({-(\ln[2.60M]-\ln[4.05M])}\over 180\)
\(k=2.46x10^{-3}\)
Séptimo Experimento
\(\ln[A]_t=-kt+\ln[A]_o\)
\(\ln[1.89M]=-k(180s)+\ln[2.95M]\)
k=\({-(\ln[1.89M]-\ln[2.95M])}\over 180\)
\(k=2.47x10^{-3}\)
Octavo experimento
\(\ln[A]_t=-kt+\ln[A]_o\)
\(\ln[1.11M]=-k(180s)+\ln[1.72M]\)
k=\({-(\ln[1.11M]-\ln[1.72M])}\over 180\)
\(k=2.43x10^{-3}\)
- Responder
-
[A] 0 (M) k × 10 3 (s −1) 4.88 2.45 3.52 2.51 2.29 2.54 1.81 2.58 5.33 2.35 4.05 2.44 2.95 2.47 1.72 2.43
Q12.4.20
Durante los últimos 10 años, el hidrocarburo insaturado 1,3-butadieno se\(\ce{(CH2=CH–CH=CH2)}\) ha clasificado en el puesto 38 entre los 50 principales productos químicos industriales. Se utiliza principalmente para la fabricación de caucho sintético. Existe también un isómero como ciclobuteno:

La isomerización de ciclobuteno a butadieno es de primer orden y la constante de velocidad se ha medido como 2.0 × 10 −4 s −1 a 150 °C en un matraz de 0.53-L. Determinar la presión parcial del ciclobuteno y su concentración después de 30.0 minutos si se realiza una reacción de isomerización a 150 °C con una presión inicial de 55 torr.
- Solución
-
Dado que se trata de una reacción de primer orden, la ley de velocidad integrada es: Presión\([A_{t}]=[A_{0}]e^{-kt}\)
parcial: Utilice la ley de velocidad integrada para encontrar la presión parcial a los 30 minutos:Use\(A_0\) = 55 torr, t = 30 min y k =\(2.0 * 10^{-4}s^{-1}\) para resolver la ecuación de la ley de tasa integrada:
\([A_{30}]=(55 torr)*e^{-(2.0x10^{-4}\frac{1}{sec})(30min\cdot\frac{60sec}{1 min})}\)
Resuelve esta ecuación para obtener:
\([A_{30}]=(55 torr)*e^{-0.36}\)
\(A_{30}]\)= 38.37 torr.
Concentración Inicial: Encuentra la concentración inicial usando la ley de gas ideal.
La ley ideal del gas viene dada por\(PV = nRT → n = \frac{PV}{RT}\). Utilice esta forma de la ley de gases para resolver para la concentración inicial n.
Usa V = 0.53L, R = 0.08206\(\frac{L*atm}{mol*L}\), T = 423.15 K, y P\(\frac{1 atm}{760}\) = 0.07237 atm.
Resuelve la ecuación de gas ideal usando estos valores:
\(n=\frac{(55torr)(0.53L)}{(0.08206\frac{L*atm}{mol*K})(423.15K)} = 0.00110\)moles de ciclobuteno.
Ahora encuentra la concentración inicial de ciclobuteno\(A_0\) usando la ecuación\([A_0] = \frac{n}{V}\):
\(A_0 = \frac{n}{V} = \frac{0.00110 moles}{0.53 L} = 0.00208 M\)
Concentración a los 30 minutos: Encuentra la concentración de ciclobuteno a los 30 minutos usando la ley de velocidad integrada dada anteriormente, usando el tiempo t = 30 minutos, o 1800 segundos.
\([A_{30}]=(0.00208M)e^{-0.36}= 0.00145M\)
Entonces, a los 30 minutos, la concentración de ciclobuteno es de 0.00145 M, y la presión parcial es de 38.37 torr.
- Responder
-
Presión Parcial: 38.37 torr.
Concentración: 0.00145 M
12.5: Teoría de colisiones
Q12.5.1
Las reacciones químicas ocurren cuando los reactivos colisionan. ¿Cuáles son dos factores que pueden impedir que una colisión produzca una reacción química?
- Solución
-
Los dos factores que pueden impedir que una colisión produzca una reacción química son:
1. Energía cinética de la molécula
Para que se produzcan reacciones químicas, las moléculas requieren suficiente velocidad para superar la mínima energía de activación necesaria para romper los viejos enlaces y formar nuevos enlaces con otras moléculas. A temperaturas más altas, las moléculas poseen la mínima cantidad de energía cinética necesaria lo que asegura que las colisiones sean lo suficientemente energéticas como para conducir a una reacción.
2. La o rientación de moléculas durante la colisión
Dos moléculas tienen que colisionar en la orientación correcta para que se produzca la reacción. Las moléculas tienen que orientarse adecuadamente para que otra molécula colisione en el estado de activación correcto.
Q12.5.2
Cuando cada colisión entre reactivos conduce a una reacción, ¿qué determina la velocidad a la que ocurre la reacción?
- Solución
-
Tiene que haber contacto entre los reactivos para que ocurra una reacción. Cuanto más chocan los reactivos, más a menudo pueden ocurrir reacciones. Los factores que determinan las velocidades de reacción incluyen la concentración de los reactivos, la temperatura, los estados físicos de los reactivos, el área superficial y el uso de un catalizador. La velocidad de reacción generalmente aumenta a medida que aumenta la concentración de un reactivo. Al aumentar la temperatura se incrementa la energía cinética promedio de las moléculas, provocando que colisionen con mayor frecuencia, lo que aumenta la velocidad de reacción. Cuando dos reactivos están en la misma fase fluida, sus partículas chocan con mayor frecuencia, lo que aumenta la velocidad de reacción. Si se aumenta el área superficial de un reactivo, se exponen más partículas al otro reactivo, por lo que se producen más colisiones y la velocidad de reacción aumenta. Un catalizador participa en una reacción química y aumenta la velocidad de reacción sin cambiarse por sí mismo.
Q12.5.3
¿Cuál es la energía de activación de una reacción y cómo se relaciona esta energía con el complejo activado de la reacción?
- Solución
-

La energía de activación es la barrera energética que se debe superar para que ocurra una reacción. Para obtener las moléculas en un estado que les permita romperse y formar enlaces, las moléculas deben ser contorsionadas (deformadas o dobladas) en un estado inestable llamado estado de transición. El estado de transición es un estado de alta energía, y se debe agregar cierta cantidad de energía —la energía de activación— para que la molécula la alcance. Debido a que el estado de transición es inestable, las moléculas reaccionantes no permanecen allí mucho tiempo, sino que pasan rápidamente al siguiente paso de la reacción química.El complejo activado es la energía más alta del estado de transición de la reacción.
Q12.5.5
Describir cómo se pueden usar métodos gráficos para determinar la energía de activación de una reacción a partir de una serie de datos que incluyen la velocidad de reacción a temperaturas variables.
- Solución
-
Este método se basa en la ecuación de Arrhenius que puede ser utilizada para mostrar el efecto de un cambio de temperatura sobre la constante de velocidad y, por lo tanto, sobre la velocidad de reacción.
La constante de velocidad es diferente de la rata de reacción en que la velocidad de reacción es la medida de qué tan rápido o lento tiene lugar una reacción química mientras que una constante de velocidad es una constante que muestra la relación entre la velocidad de reacción y las concentraciones de los reactivos o productos.
Por ejemplo, para la reacción\(A + B \rightarrow C\), the rate law would be:
\(rate = k[A]^a[B]^b\)
k = constante de velocidad
[A] = concentración de reactivo A
a = orden de reacción con respecto a A
[B] = concentración de reactivo B
b = orden de reacción con respecto a B
Sin embargo, la constante de velocidad permanece constante solo si se está cambiando la concentración de los reactivos. Si cambia la temperatura o el catalizador de la reacción, la constante de velocidad cambiará y esto se demuestra por la ecuación de Arrhenius:
\(k = Ae^\frac{-E_a}{RT}\)
\(ln \left(\frac{k_1}{k_2}\right) = \left(\frac{-E_a}{R}\right)\left(\frac{1}{T_1} - \frac{1}{T_2}\right)\)
k = constante de velocidad
A = factor de frecuencia
\(E_a\) = activation energy
e = función exponencial,\(e^x\)
R = constante de gas
T = temperatura (K)

En otras palabras, la energía de activación de una reacción,\(E_a\), from a series of data that includes the rate of reaction, k, at varying temperatures can be determined by graphing it on a plot of \(\ln k\) versus \(\frac{1}{T}\). You can then use the slope of the graph you have plotted to solve for \(E_a\) by setting the slope equal to \(\frac{-E_a}{R}\).
Q12.5.6
How does an increase in temperature affect rate of reaction? Explain this effect in terms of the collision theory of the reaction rate.
S12.5.6
Collision theory states that the rates of chemical reactions depend on the fraction of molecules with the correct orientation, fraction of collisions with required energy, and the collision frequency. Because the fraction of collisions with required energy is a function of temperature, as temperature increases, the fraction of collisions with required energy also increases. The kinetic energy of reactants also increases with temperature which means molecules will collide more often increasing collisions frequency. With increased fraction of collisions with required energy and collisions frequency, the rate of chemical reaction increases. We see mathematically, from the Arrhenius equation, that temperature and the rate constant are related.
\[k=Ae^{\frac {E_a}{RT}}\]
where k is the rate constant, A is a specific constant, R is 8.3145 J/K, Ea is the reaction-specific activation energy in J, and T is temperature in K. We see from the equation that k is very sensitive to changes in the temperature.
Q12.5.7
The rate of a certain reaction doubles for every 10 °C rise in temperature.
- How much faster does the reaction proceed at 45 °C than at 25 °C?
- How much faster does the reaction proceed at 95 °C than at 25 °C?
- Solution
-
By finding the difference in temperature, 45 °C - 25 °C, we get 20 °C. Since the rate of the reaction doubles every 10 °C increase in temperature and the rate of the reaction experienced a 20 °C increase in temperature, we see that the reaction rate doubled twice (22 = 4). As a result, the reaction proceeds four times faster.
Following the same process as in part a, we get the difference in temperature to be 70 °C. Since the rate of the reaction doubles every 10 °C increase in temperature and the system experienced a 70 °C change, we see that the reaction doubled seven times (27 = 128). We can see the reaction proceeds 128 times faster.
(a) 4-times faster (b) 128-times faster
Q12.5.8
In an experiment, a sample of NaClO3 was 90% decomposed in 48 min. Approximately how long would this decomposition have taken if the sample had been heated 20 °C higher?
S12.5.8
First off, it is important to recognize that this decomposition reaction is a first-order reaction, which can be written as follows: \(\mathrm2NaClO_3\to2NaCl + 3O_2\)
Understanding this, it is important to be able to then be able to recognize which equation would be most useful given the initial conditions presented by the question. Since we are dealing with time, percentage of material left, and temperature, the only viable equation that could relate all of this would be the Arrhenius Equation, which is written as follows: \(\mathrm \ln(\frac{k_2}{k_1}) = \frac {Ea}{R}({\frac1{t_1}}-{\frac{1}{t_{2}}})\)
However, this problem does not give us enough information such as what the activation energy is or the initial temperature in order to mathematically solve this problem. Additionally, the problem tells us to approximate how long the decomposition would take, which means we are asked to answer this question conceptually based on our knowledge of thermodynamics and reaction rates. As a general rule of thumb, we know that for every 10˚C rise in temperature the rate of reaction doubles. Since the question tells us that there is a 20˚C rise in temperature we can deduce that the reaction rate doubles twice, as per the general rule mentioned before. This means the overall reaction rate for this decomposition would quadruple, or would be 4 times faster than the reaction rate at the initial temperature.
We can gut check this answer by recalling how an increase in the average kinetic energy (temperature) decreases the time it takes for the reaction to take place and increase the reaction rate. Thus, if we increase the temperature we should have a faster reaction rate.
Q12.5.9
The rate constant at 325 °C for the decomposition reaction \(\ce{C4H8⟶2C2H4}\) is 6.1 × 10−8 s−1, and the activation energy is 261 kJ per mole of C4H8. Determine the frequency factor for the reaction.
- Solution
-
S12.5.9
Using the Arrhenius equation allows me to find the frequency factor, A.
k=Ae-Ea/RT
k, Ea, R, and T are all known values. k, Ea, and T are given in the problem as 6.1x10-8, 261 kJ, and 598 K, respectively.
So, plugging them into the equation gives:
6.1x10-8 s-1=Ae(-261000 J)/(8.3145 J/mol)(598 K)
Take e(-261000 J)/(8.3145 J/mol)(598) and get 1.59 x 10-23. Divide k, 6.1 x 10-8, by 1.59 x 10-23 and get A=3.9 x 1015s-1
-
A12.5.9
\(\mathrm{3.9×10^{15}\:s^{−1}}\)
Q12.5.10
The rate constant for the decomposition of acetaldehyde (CH3CHO), to methane (CH4), and carbon monoxide (CO), in the gas phase is 1.1 × 10−2 L/mol/s at 703 K and 4.95 L/mol/s at 865 K. Determine the activation energy for this decomposition.
S12.5.10
The equation for relating the rate constant and activation energy of a reaction is the Arrhenius equation:
\[k = Ae^ {-\frac{E_a}{RT}}\]
When given two rate constants at two different temperatures but for the same reaction, the Arrhenius equation can be rewritten as:
\[ln (\frac{k_2}{k_1}) = \frac{E_a}{R} (\frac{1}{T_1} - \frac{1}{T_2})\]
In this problem, all the variables are given except for the Ea (activation energy).
k1 = 1.1 × 10−2 L/mol/s
T1 = 703 K
k2 = 4.95 L/mol/s
T2 = 865 K
R = 8.314 J/(mol K) (Ideal Gas Constant)
Now plug in all these values into the equation, and solve for Ea.
\[ln (\frac{4.95\frac{L}{mol×s}}{1.1 × 10^{-2}\frac{L}{mol×s}}) = \frac{E_a}{8.314 × 10^{-3}\frac{kJ}{mol×K}} (\frac{1}{703} - \frac{1}{865})\]
Ea = 190 kJ (2 sig figs)
Q12.5.11
An elevated level of the enzyme alkaline phosphatase (ALP) in the serum is an indication of possible liver or bone disorder. The level of serum ALP is so low that it is very difficult to measure directly. However, ALP catalyzes a number of reactions, and its relative concentration can be determined by measuring the rate of one of these reactions under controlled conditions. One such reaction is the conversion of p-nitrophenyl phosphate (PNPP) to p-nitrophenoxide ion (PNP) and phosphate ion. Control of temperature during the test is very important; the rate of the reaction increases 1.47 times if the temperature changes from 30 °C to 37 °C. What is the activation energy for the ALP–catalyzed conversion of PNPP to PNP and phosphate?
- Solution
-
43.0 kJ/mol
Q12.5.12
In terms of collision theory, to which of the following is the rate of a chemical reaction proportional?
- the change in free energy per second
- the change in temperature per second
- the number of collisions per second
- the number of product molecules
Q12.5.13
Hydrogen iodide, HI, decomposes in the gas phase to produce hydrogen, H2, and iodine, I2. The value of the rate constant, k, for the reaction was measured at several different temperatures and the data are shown here:
| Temperature (K) | k (M−1 s−1) |
|---|---|
| 555 | 6.23 × 10−7 |
| 575 | 2.42 × 10−6 |
| 645 | 1.44 × 10−4 |
| 700 | 2.01 × 10−3 |
What is the value of the activation energy (in kJ/mol) for this reaction?
- Solution
-
177 kJ/mol
Q12.5.14
The element Co exists in two oxidation states, Co(II) and Co(III), and the ions form many complexes. The rate at which one of the complexes of Co(III) was reduced by Fe(II) in water was measured. Determine the activation energy of the reaction from the following data:
| T (K) | k (s−1) |
|---|---|
| 293 | 0.054 |
| 298 | 0.100 |
Q12.5.15
The hydrolysis of the sugar sucrose to the sugars glucose and fructose,
\[\ce{C12H22O11 + H2O ⟶ C6H12O6 + C6H12O6}\nonumber \]
follows a first-order rate equation for the disappearance of sucrose: Rate = k[C12H22O11] (The products of the reaction, glucose and fructose, have the same molecular formulas but differ in the arrangement of the atoms in their molecules.)
- In neutral solution, k = 2.1 × 10−11 s−1 at 27 °C and 8.5 × 10−11 s−1 at 37 °C. Determine the activation energy, the frequency factor, and the rate constant for this equation at 47 °C (assuming the kinetics remain consistent with the Arrhenius equation at this temperature).
- When a solution of sucrose with an initial concentration of 0.150 M reaches equilibrium, the concentration of sucrose is 1.65 × 10−7 M. How long will it take the solution to reach equilibrium at 27 °C in the absence of a catalyst? Because the concentration of sucrose at equilibrium is so low, assume that the reaction is irreversible.
- Why does assuming that the reaction is irreversible simplify the calculation in part (b)?
- Solution
-
Ea = 108 kJ
A = 2.0 × 108 s−1
k = 3.2 × 10−10 s−1
(b) 1.81 × 108 h or 7.6 × 106 day. (c) Assuming that the reaction is irreversible simplifies the calculation because we do not have to account for any reactant that, having been converted to product, returns to the original state.
Q12.5.16
Use the PhET Reactions & Rates interactive simulation to simulate a system. On the “Single collision” tab of the simulation applet, enable the “Energy view” by clicking the “+” icon. Select the first \(A+BC⟶AB+C\) reaction (A is yellow, B is purple, and C is navy blue). Using the “straight shot” default option, try launching the A atom with varying amounts of energy. What changes when the Total Energy line at launch is below the transition state of the Potential Energy line? Why? What happens when it is above the transition state? Why?
Q12.5.17
Use the PhET Reactions & Rates interactive simulation to simulate a system. On the “Single collision” tab of the simulation applet, enable the “Energy view” by clicking the “+” icon. Select the first \(A+BC⟶AB+C\) reaction (A is yellow, B is purple, and C is navy blue). Using the “angled shot” option, try launching the A atom with varying angles, but with more Total energy than the transition state. What happens when the A atom hits the BC molecule from different directions? Why?
- Solution
-
The A atom has enough energy to react with BC; however, the different angles at which it bounces off of BC without reacting indicate that the orientation of the molecule is an important part of the reaction kinetics and determines whether a reaction will occur.
12.6: Reaction Mechanisms
Q12.6.1
Why are elementary reactions involving three or more reactants very uncommon?
Q12.6.2
In general, can we predict the effect of doubling the concentration of A on the rate of the overall reaction \(A+B⟶C\) ? Can we predict the effect if the reaction is known to be an elementary reaction?
- Solution
-
Add texts here. Do not delete this text first.
No. In general, for the overall reaction, we cannot predict the effect of changing the concentration without knowing the rate equation. Yes. If the reaction is an elementary reaction, then doubling the concentration of A doubles the rate.
Q12.6.3
Phosgene, COCl2, one of the poison gases used during World War I, is formed from chlorine and carbon monoxide. The mechanism is thought to proceed by:
| step 1: | Cl + CO → COCl |
| step 2: | COCl + Cl2→ COCl2 + Cl |
- Write the overall reaction equation.
- Identify any reaction intermediates.
- Identify any intermediates.
Q12.6.4
Define these terms:
- unimolecular reaction
- bimolecular reaction
- elementary reaction
- overall reaction
Q12.6.5
What is the rate equation for the elementary termolecular reaction \(A+2B⟶\ce{products}\)? For \(3A⟶\ce{products}\)?
- Solution
-
Add texts here. Do not delete this text first.
We are given that both of these reactions are elementary termolecular. The molecularity of a reaction refers to the number of reactant particles that react together with the proper and energy and orientation. Termolecular reactions have three atoms to collide simultaneously. As it is termolecular, and there are no additional reactants aside from the three given in each reaction, there are no intermediate reactions. The rate law for elementary reactions is determined by the stoichiometry of the reaction without needed experimental data.
The basic rate form for the elementary step is what follows:
\(rate= {k} \cdot {reactant \ 1}^{i} \cdot {reactant \ 2}^{ii} \cdot ... \) Where i and ii are the stochiometric coefficient from reactant 1 and 2 respectively.
For: \(3A \rightarrow products \)
\({k} \cdot {A}^3 = rate\)
For: \(A + 2B \rightarrow products \)
\({k} \cdot {[A]} \cdot {[B]}^2 = rate\)
Note that the order of these reactions are both three.
- Answer
-
Add texts here. Do not delete this text first.
Rate = k[A][B]2; Rate = k[A]3
Q12.6.6
Given the following reactions and the corresponding rate laws, in which of the reactions might the elementary reaction and the overall reaction be the same?
(a) \(\ce{Cl2 + CO ⟶ Cl2CO}\)
\(\ce{rate}=k\ce{[Cl2]^{3/2}[CO]}\)
(b) \(\ce{PCl3 + Cl2 ⟶ PCl5}\)
\(\ce{rate}=k\ce{[PCl3][Cl2]}\)
(c) \(\ce{2NO + H2 ⟶ N2 + H2O}\)
\(\ce{rate}=k\ce{[NO][H2]}\)
(d) \(\ce{2NO + O2 ⟶ 2NO2}\)
\(\ce{rate}=k\ce{[NO]^2[O2]}\)
(e) \(\ce{NO + O3 ⟶ NO2 + O2}\)
\(\ce{rate}=k\ce{[NO][O3]}\)
- Solution
-
Add texts here. Do not delete this text first.
An elementary reaction is a chemical reaction in which the reactants directly form products in a single step. In another words, the rate law for the overall reaction is same as experimentally found rate law. Out of 5 options, option (b),(d), and (e) are such reactions
Q12.6.7
Write the rate equation for each of the following elementary reactions:
- \(\ce{O3 \xrightarrow{sunlight} O2 + O}\)
- \(\ce{O3 + Cl ⟶ O2 + ClO}\)
- \(\ce{ClO + O⟶ Cl + O2}\)
- \(\ce{O3 + NO ⟶ NO2 + O2}\)
- \(\ce{NO2 + O ⟶ NO + O2}\)
- Solution
-
Add texts here. Do not delete this text first.
Rate equations are dependent on the reactants and not the products.
The rate law of a reaction can be found using a rate constant (which is found experimentally), and the initial concentrations of reactants.
A general solution for the equation
\(aA + bB \rightarrow cC + dD\)
is \(rate = k[A]^{m}[B]^{n}\) where m and n are reaction orders.
However, reaction orders are found experimentally, and since we do not have experimental data for these reactions, we can disregard that part of the equation.
To find the rate laws, all we have to do is plug the reactants into the rate formula. This is only due to the case that these are elementary reactions. Further reading on elementary reactions can be found on Libre Texts.
a. O3 ⟶ O2 + O
To write this reaction's rate equation, only focus on the reactant(s) and its/their concentration and multiplying that by a rate constant, "k".
Rate = k[O3]
b. O3 + Cl ⟶ O2 + ClO
To write this reaction's rate equation, only focus on the reactant(s) and its/their concentration and multiplying that by a rate constant, "k".
Rate = k[O3][Cl]
c. ClO + O ⟶ Cl + O2
To write this reaction's rate equation, only focus on the reactant(s) and its/their concentration and multiplying that by a rate constant, "k".
Rate = k[ClO][O]
d. O3 + NO ⟶ NO2 + O2
To write this reaction's rate equation, only focus on the reactant(s) and its/their concentration and multiplying that by a rate constant, "k".
Rate = k[O3][NO]
e. NO2 + O ⟶ NO + O2
To write this reaction's rate equation, only focus on the reactant(s) and its/their concentration and multiplying that by a rate constant, "k".
Rate = k[NO2][O]
- Answer
-
Add texts here. Do not delete this text first.
(a) Rate1 = k[O3]; (b) Rate2 = k[O3][Cl]; (c) Rate3 = k[ClO][O]; (d) Rate2 = k[O3][NO]; (e) Rate3 = k[NO2][O]
Q12.6.8
Nitrogen(II) oxide, NO, reacts with hydrogen, H2, according to the following equation:
\[\ce{2NO + 2H2 ⟶ N2 + 2H2O}\nonumber \]
What would the rate law be if the mechanism for this reaction were:
\[\ce{2NO + H2 ⟶ N2 + H2O2\:(slow)}\nonumber \]
\[\ce{H2O2 + H2 ⟶ 2H2O\:(fast)}\nonumber \]
The rate law of the mechanism is determined by the slow step of the reaction. Since the slow step is an elementary step, the rate law can be drawn from the coefficients of the chemical equation. So therefore, the rate law is as follows: rate=k[NO]2[H2]. Since both NO and H2 are reactants in the overall reaction (therefore are not intermediates in the reaction), no further steps have to be done to determine the rate law.
Q12.6.9
Consider the reaction
CH4 + Cl2 → CH3Cl + HCl (occurs under light)
The mechanism is a chain reaction involving Cl atoms and CH3 radicals. Which of the following steps does not terminate this chain reaction?
- CH3 + Cl → CH3CI
- CH3 + HCl → CH4 + Cl
- CH3 + CH3 → C2H2
- Cl + Cl → Cl2
- Solution
-
Add texts here. Do not delete this text first.
Chain reactions involve reactions that create products necessary for more reactions to occur. In this case, a reaction step will continue the chain reaction if a radical is generated. Radicals are highly reactive particles, so more reactions in the chain will take place as long as they are present. The chlorine is considered a free radical as it has an unpaired electron; for this reason it is very reactive and propagates a chain reaction. It does so by taking an electron from a stable molecule and making that molecule reactive, and that molecule goes on to react with stable species, and in that manner a long series of "chain" reactions are initiated. A chlorine radical will continue the chain by completing the following reaction:
\({Cl \cdot}+{CH_4} \rightarrow {CH_3 \cdot}+{HCl} \)
The \({CH_3}\) generated by this reaction can then react with other species, continuing to propagate the chain reaction.
Option 1 is incorrect because the only species it produces is \({CH_3Cl}\), a product in the overall reaction that is unreactive. This terminates the chain reaction because it fails to produce any \(Cl\) or \(CH_3\) radicals that are necessary for further propagating the overall reaction.
Option 2 is the correct answer because it produces a \(Cl\) radical. This \(Cl\) radical can continue the chain by colliding with \(CH_4\) molecules.
Option 3 is incorrect because it fails to produce a radical capable of continuing the chain.
Option 4 is incorrect because it produces \(Cl_2\), a molecule that does not react unless additional light is supplied. Therefore, this step breaks the chain.
- Answer
-
Add texts here. Do not delete this text first.
Answer: Option 2: \({CH_3}+{HCl} \rightarrow {CH_4}+{Cl}\)
Q12.6.10
Experiments were conducted to study the rate of the reaction represented by this equation.
\[\ce{2NO}(g)+\ce{2H2}(g)⟶\ce{N2}(g)+\ce{2H2O}(g)\nonumber \]
Initial concentrations and rates of reaction are given here.
| Experiment | Initial Concentration [NO] (mol/L) | Initial Concentration, [H2] (mol/L) | Initial Rate of Formation of N2 (mol/L min) |
|---|---|---|---|
| 1 | 0.0060 | 0.0010 | 1.8 × 10−4 |
| 2 | 0.0060 | 0.0020 | 3.6 × 10−4 |
| 3 | 0.0010 | 0.0060 | 0.30 × 10−4 |
| 4 | 0.0020 | 0.0060 | 1.2 × 10−4 |
Consider the following questions:
- Determine the order for each of the reactants, NO and H2, from the data given and show your reasoning.
- Write the overall rate law for the reaction.
- Calculate the value of the rate constant, k, for the reaction. Include units.
- For experiment 2, calculate the concentration of NO remaining when exactly one-half of the original amount of H2 had been consumed.
- The following sequence of elementary steps is a proposed mechanism for the reaction.
Step 1: \(\ce{NO + NO ⇌ N2O2}\)
Step 2: \(\ce{N2O2 + H2 ⇌ H2O + N2O}\)
Step 3: \(\ce{N2O + H2 ⇌ N2 + H2O}\)
Based on the data presented, which of these is the rate determining step? Show that the mechanism is consistent with the observed rate law for the reaction and the overall stoichiometry of the reaction.
S12.6.10
1. i) Find the order for [NO] by using experiment 3 and 4 where [H2] is constant
Notice that [NO] doubles from experiment 3 to 4 and the rate quadruples. So the order for [NO] is 2
ii) Find the order for [H2] by using experiment 1 and 2 where [NO] is constant
Notice that [H2] doubles from experiment 1 to 2 and the rate doubles as well. So the order for [H2] is 1
2. Put in the order for each product as the exponents for the corresponding reactant.
\(rate = k [NO]^2 [H_2]\)
3. Put in the concentrations and the rate from one of the experiments into the rate law and solve for k. (Here, experiement 1 is used but any of them will work)
\(rate = k [NO]^2 [H_2]\) \(.00018 = k [.006]^2 [.001]\) \(k = 5000 M^{-2}s^{-1}\)
4. Plug in values for experiment 2 into the rate law equation and solve for the concentration of NO
\(.00036=5000[NO]^2[.001]\) \([NO]^2= 7.2 x 10^{-5}\) \([NO] = .0085 M\)
5. Write the rate laws for each step and then see which matches the rate law we found in question 2. The rate determining step (the slow step) is the one that gives the rate for the overall reaction. Because of this, only those concentrations will influence the overall reaction, contrary to what we would believe if we just looked at the overall reaction.
Step 1: \(NO + NO \rightleftharpoons N_2O_2\)
\(rate =k_1[NO]^2\) This rate law is not the same as the one we calculate in question 2 so this can not be the rate determining step
Step 2: \(N_2O_2+H_2 \rightleftharpoons N_2O + N_2O\)
\(rate = k_2[N_2O_2][H_2]\)
Since \(N_2O_2\) is an intermediate you must replace it in the rate law equation. Intermediates can not be in the rate law because they do not appear in the overall reaction. Here you can take the reverse of equation 1 (k-1) and substitute the other side (the reactants of equation 1) for the intermediate in the rate law equation.
\[rate_1 = rate_{-1}\nonumber \]
\[k_1[NO]^2 = k_{-1}[N_2O_2]\nonumber \]
\[[N_2O_2] = \frac{k_1[NO]^2}{k_{-1}}\nonumber \]
\(rate= \frac{k_2k_{1}[NO]^2[H_2]}{k_{-1}}\)
Overall: \(rate={k[NO]^2[H_2]}\) This is the same so it is the rate determining step.
So \(N_2O_2+H_2 \rightleftharpoons N_2O + N_2O\) is the rate determining step step.
- Answer
-
Add texts here. Do not delete this text first.
(a) NO: 2
\(\ce {H2}\) : 1
(b) Rate = k [NO]2[H2];
(c) k = 5.0 × 103 mol−2 L−2 min−1;
(d) 0.0050 mol/L;
(e) Step II is the rate-determining step.
Q12.6.11
The reaction of CO with Cl2 gives phosgene (COCl2), a nerve gas that was used in World War I. Use the mechanism shown here to complete the following exercises:
- \(\ce{Cl2}(g)⇌\ce{2Cl}(g)\) (fast, k1 represents the forward rate constant, k−1 the reverse rate constant)
- \(\ce{CO}(g)+\ce{Cl}(g)⟶\ce{COCl}(g)\) (slow, k2 the rate constant)
- \(\ce{COCl}(g)+\ce{Cl}(g)⟶\ce{COCl2}(g)\) (fast, k3 the rate constant)
- Write the overall reaction.
- Identify all intermediates.
- Write the rate law for each elementary reaction.
- Write the overall rate law expression.
- Solution
-
Add texts here. Do not delete this text first.
1. To write the overall reaction you have to identify the intermediates and leave them out. The easiest way to do this is to write out all the products and reactants and cross out anything that is on both sides.
Cl2(g) + CO(g) + 2Cl(g) +COCl(g) ⇒ 2Cl(g) + COCl(g) + COCl2(g)
In this you will cross out the 2Cl(g) molecules and the COCl(g). What is left after that is the overall reaction.
Cl2(g) + CO(g) ⇒ + COCl2(g)
2. For part two you will just list the intermediates that you crossed out.
Cl and COCl are intermediates
3. Each rate law will be the rate equal to the rate constant times the concentrations of the reactants
reaction 1
(forward) rate=k1[Cl2] ( reverse) rate=k-1[Cl]
reaction 2
rate=k2[CO][Cl]
Reaction 3
rate=k3[COCl][Cl]
4. The overall rate law is based off the slowest step (step #2), since it is the rate determining step, but Cl is present in that rate law so we have to replace it with an equivalent that does not contain an intermediate. To do this you use the equilibrium since the rates are the same you can set up the rate laws of the forward and reverse equal to each other.
k1[Cl2] = k-1[Cl]
[Cl]= k1[Cl2]/k-1
rate=k2[CO]k1[Cl2]/k-1
rate=k°[CO][Cl2]
Steps to replacing and intermediate
- Set the forward and reverse reaction equal to each other using separate constants
- Solve for the intermediate using algebra
- Plug into the rate determining formula
- All the k's will be condensed into a K prime constant
12.7: Catalysis
Q12.7.1
Account for the increase in reaction rate brought about by a catalyst.
Q12.7.2
Compare the functions of homogeneous and heterogeneous catalysts.
Q12.7.3
Consider this scenario and answer the following questions: Chlorine atoms resulting from decomposition of chlorofluoromethanes, such as CCl2F2, catalyze the decomposition of ozone in the atmosphere. One simplified mechanism for the decomposition is: \[\ce{O3 \xrightarrow{sunlight} O2 + O}\\ \ce{O3 + Cl ⟶ O2 + ClO}\\ \ce{ClO + O ⟶ Cl + O2}\nonumber \]
- Explain why chlorine atoms are catalysts in the gas-phase transformation: \[\ce{2O3⟶3O2}\nonumber \]
- Nitric oxide is also involved in the decomposition of ozone by the mechanism: \[\ce{O3 \xrightarrow{sunlight} O2 + O\\ O3 + NO ⟶ NO2 + O2\\ NO2 + O ⟶ NO + O2}\nonumber \]
Is NO a catalyst for the decomposition? Explain your answer.
Q12.7.4
For each of the following pairs of reaction diagrams, identify which of the pair is catalyzed:
(a)
Q12.7.5
For each of the following pairs of reaction diagrams, identify which of the pairs is catalyzed:
(a)
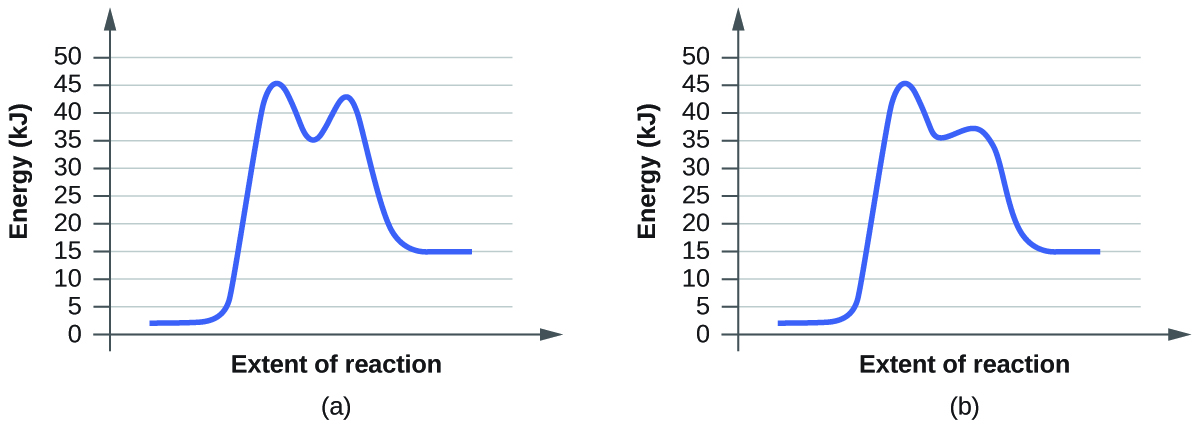
(b)
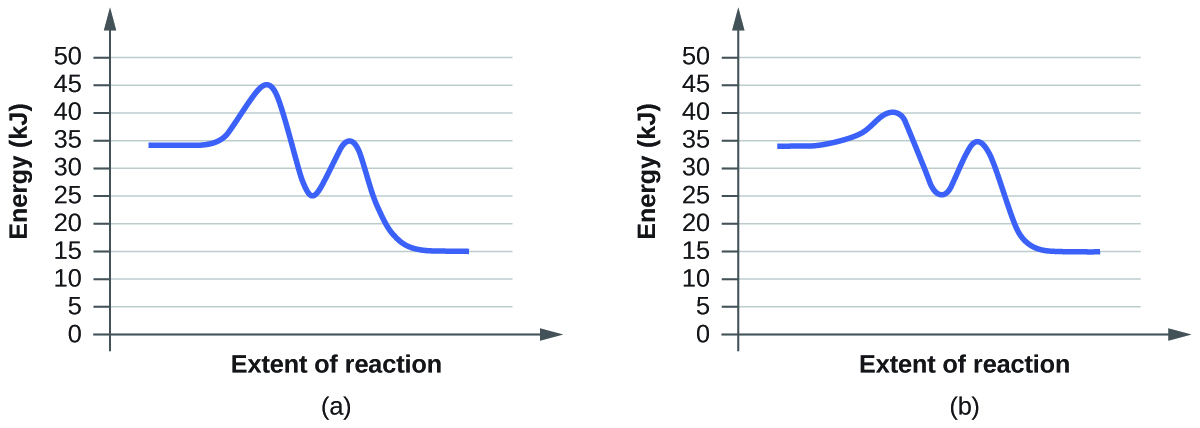
Q12.7.6
For each of the following reaction diagrams, estimate the activation energy (Ea) of the reaction:
(a)
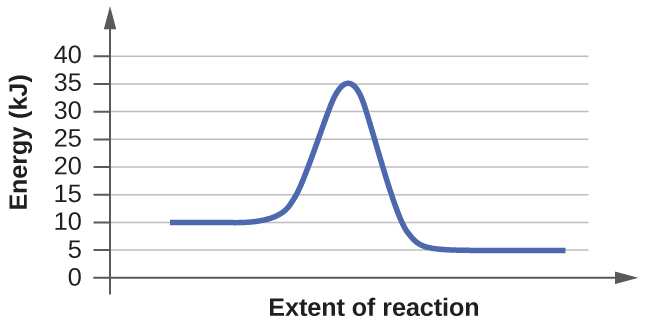
(b)
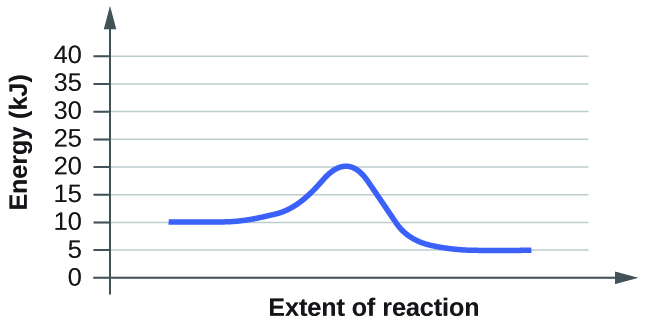
Q12.7.7
For each of the following reaction diagrams, estimate the activation energy (Ea) of the reaction:
(a)

(b)
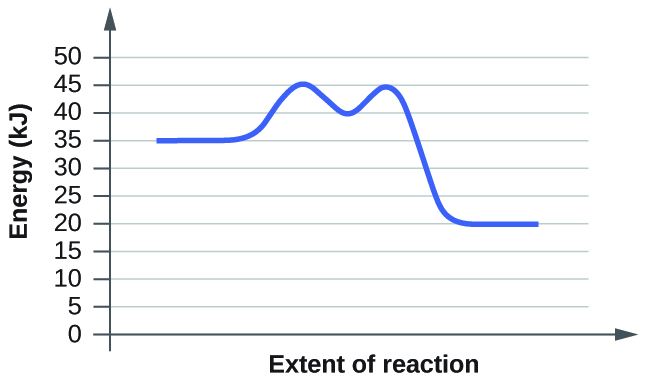
Q12.7.8
- Based on the diagrams in Question Q12.7.6, which of the reactions has the fastest rate? Which has the slowest rate?
- Based on the diagrams in Question Q12.7.7, which of the reactions has the fastest rate? Which has the slowest rate?



![{\ displaystyle t_ {\ frac {1} {2}} = {\ frac {1} {k {\ ce {[A] 0}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b25f9b5e7675b3e3f9027241a74ec2d751810c43)