Saltar al contenido principal
LibreTexts Español

4.7: Distribución Desigual - Enlaces Covalentes Polares

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    72247

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Objetivos de aprendizaje
    • Definir electronegatividad
    • Determinar la polaridad de un enlace covalente.

    Electronegatividad

    La capacidad de un átomo en una molécula para atraer electrones compartidos se llama electronegatividad. Cuando dos átomos se combinan, la diferencia entre sus electronegatividades es una indicación del tipo de enlace que se formará. Si la diferencia entre las electronegatividades de los dos átomos es pequeña, ninguno de los dos átomos puede alejar completamente los electrones compartidos del otro átomo y el enlace será covalente. Si la diferencia entre las electronegatividades es grande, el átomo más electronegativo alejará completamente a los electrones de enlace del otro átomo (se producirá la transferencia de electrones) y el enlace será iónico. Esta es la razón por la cual los metales (bajas electronegatividades) unidos con no metales (altas electronegatividades) típicamente producen compuestos iónicos.

    Un enlace puede ser tan polar que un electrón realmente se transfiere de un átomo a otro, formando un verdadero enlace iónico. ¿Cómo juzgamos el grado de polaridad? Los científicos han ideado una escala llamada electronegatividad, una escala para juzgar cuánto átomos de cualquier elemento atraen electrones. La electronegatividad es un número sin unidades; cuanto mayor es el número, más atrae un átomo a los electrones. Una escala común para electronegatividad se muestra en la Figura\(\PageIndex{1}\).

    alt
    Figura\(\PageIndex{1}\) Electronegatividades de los Elementos. Las electronegatividades se utilizan para determinar la polaridad de los enlaces covalentes.

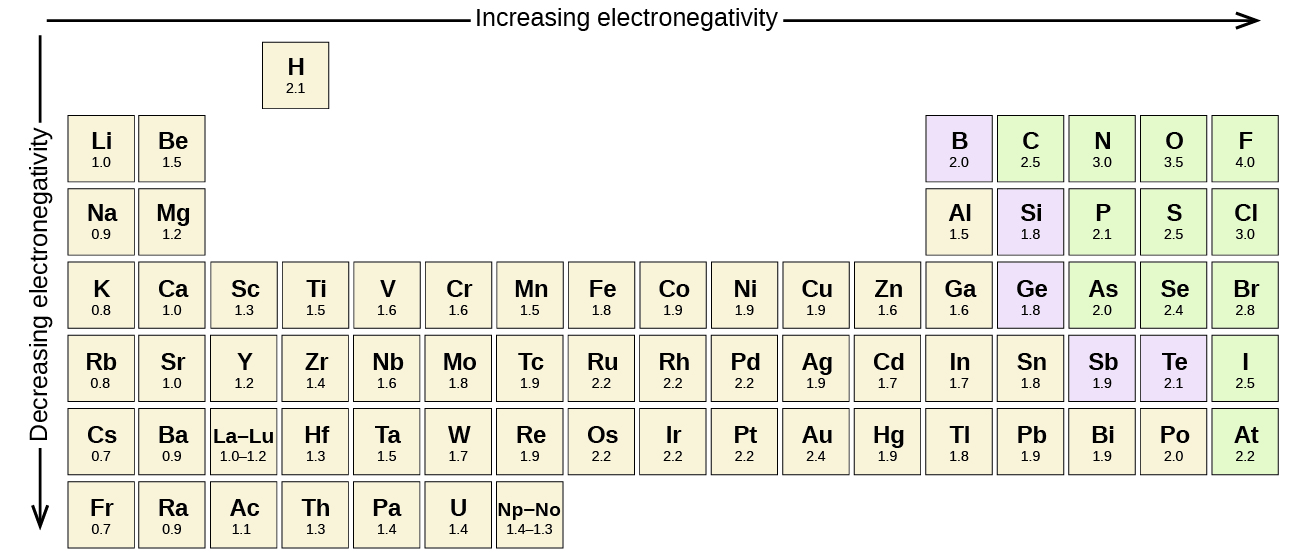
    Polaridad de enlace

    La polaridad de un enlace covalente puede juzgarse determinando la diferencia de las electronegatividades de los dos átomos involucrados en el enlace covalente, como se resume en la siguiente tabla:

    \(\PageIndex{1}\)Tabla:Diferencias de electronegatividad y tipo de enlace
    Diferencia de electronegatividad Tipo de enlace
    0 covalente no polar
    0—0.4 covalente ligeramente polar
    0.5—2.0 definitivamente covalente polar
    >2.0 probablemente iónico

    Enlaces covalentes no polares

    Un enlace en el que la diferencia de electronegatividad es menor de 1.9 se considera que es mayormente de carácter covalente. Sin embargo, en este punto necesitamos distinguir entre dos tipos generales de enlaces covalentes. Un enlace covalente no polar es un enlace covalente en el que los electrones de enlace se comparten por igual entre los dos átomos. En un enlace covalente no polar, la distribución de la carga eléctrica se equilibra entre los dos átomos.

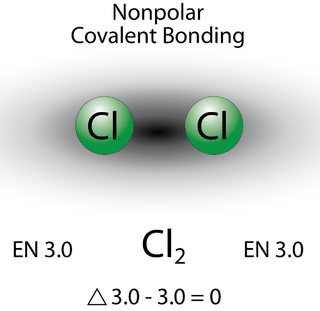
    Figura\(\PageIndex{2}\) Un enlace covalente no polar es aquel en el que la distribución de la densidad electrónica entre los dos átomos es igual.

    Los dos átomos de cloro comparten el par de electrones en el enlace covalente simple por igual, y la densidad de electrones que rodea a la\(\ce{Cl_2}\) molécula es simétrica. También hay que señalar que las moléculas en las que la diferencia de electronegatividad es muy pequeña (<0.5) también se consideran covalentes no polares. Un ejemplo sería un enlace entre cloro y bromo (\(\Delta\)EN\(=3.0 - 2.8 = 0.2\)).

    Enlaces covalentes polares

    Un enlace en el que la diferencia de electronegatividad entre los átomos está entre 0.5 y 2.0 se denomina enlace covalente polar. Un enlace covalente polar es un enlace covalente en el que los átomos tienen una atracción desigual por los electrones y por lo tanto la compartición es desigual. En un enlace covalente polar, a veces simplemente llamado enlace polar, la distribución de electrones alrededor de la molécula ya no es simétrica.

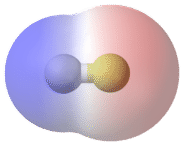
    Figura\(\PageIndex{3}\) En el enlace covalente polar de\(\ce{HF}\), la densidad electrónica está distribuida de manera desigual. Hay una densidad más alta (roja) cerca del átomo de flúor, y una densidad menor (azul) cerca del átomo de hidrógeno.

    Una manera fácil de ilustrar la distribución desigual de electrones en un enlace covalente polar es usar la letra griega delta\(\left( \delta \right)\).

    Figura\(\PageIndex{4}\) Uso de\(\delta\) para indicar carga parcial.

    El átomo con mayor electronegatividad adquiere una carga negativa parcial, mientras que el átomo con la electronegatividad menor adquiere una carga positiva parcial. El símbolo delta se utiliza para indicar que la cantidad de carga es menor a uno. También se puede utilizar una flecha cruzada para indicar la dirección de mayor densidad electrónica.

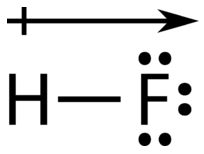
    Figura\(\PageIndex{5}\) Uso de flecha cruzada para indicar polaridad

    Diferencias de electronegatividad en la unión usando escala Pauling. Usar diferencias en la electronegatividad para clasificar los enlaces como covalentes, covalentes polares o iónicos.

    Ejemplo\(\PageIndex{1}\): Bond Polarity

    ¿Cuál es la polaridad de cada enlace?

    1. C—H
    2. O—H
    Solución

    Usando Figura\(\PageIndex{1}\), podemos calcular la diferencia de las electronegatividades de los átomos involucrados en el enlace.

    1. Para el enlace C—H, la diferencia en las electronegatividades es 2.5 − 2.1 = 0.4. Así predecimos que este enlace será covalente no polar.
    2. Para el enlace O—H, la diferencia en electronegatividades es 3.5 − 2.1 = 1.4, por lo que predecimos que este enlace será definitivamente covalente polar.
    Ejercicio\(\PageIndex{1}\)

    ¿Cuál es la polaridad de cada enlace?

    1. Rb—F
    2. P—Cl
    Responder a

    probablemente iónico

    Respuesta b

    covalente polar

    Resumen

    • El tipo de enlace (covalente polar, covalente no polar o iónico) entre dos átomos está determinado por las diferencias en la electronegatividad.
    • Para los átomos que comparten un enlace covalente polar, el átomo con mayor electronegatividad adquiere una carga negativa parcial, mientras que el átomo con la electronegatividad menor adquiere una carga positiva parcial.

    Colaboradores y Atribuciones

    4.7: Distribución Desigual - Enlaces Covalentes Polares is shared under a not declared license and was authored, remixed, and/or curated by LibreTexts.