8.2: Gravimetría de precipitación

En la gravimetría de precipitación se forma un compuesto insoluble cuando añadimos un reactivo precipitante, o precipitante, a una solución que contiene nuestro analito. En la mayoría de los casos el precipitado es producto de una simple reacción de metátesis entre el analito y el precipitante; sin embargo, cualquier reacción que genere un precipitado potencialmente puede servir como método gravimétrico.

La mayoría de los métodos gravimétricos de precipitación se desarrollaron en el siglo XIX, o antes, a menudo para el análisis de minerales. La Figura 1.1.1 del Capítulo 1, por ejemplo, ilustra un método gravimétrico de precipitación para el análisis de níquel en minerales.

Teoría y Práctica

Todos los análisis gravimétricos de precipitación comparten dos atributos importantes. Primero, el precipitado debe ser de baja solubilidad, de alta pureza y de composición conocida para que su masa refleje con precisión la masa del analito. Segundo, debe ser fácil separar el precipitado de la mezcla de reacción.

Consideraciones de solubilidad

Para proporcionar un resultado preciso, la solubilidad de un precipitado debe ser mínima. La precisión de una técnica de análisis total típicamente es mejor que ± 0.1%, lo que significa que el precipitado debe representar al menos 99.9% del analito. Extender este requisito al 99.99% asegura que la solubilidad del precipitado no limitará la precisión de un análisis gravimétrico.

Una técnica de análisis total es aquella en la que la señal analítica —masa en este caso— es proporcional a la cantidad absoluta de analito en la muestra. Consulte el Capítulo 3 para una discusión de la diferencia entre las técnicas de análisis total y las técnicas de concentración.

Podemos minimizar las pérdidas de solubilidad controlando las condiciones bajo las cuales se forma el precipitado. Esto, a su vez, requiere que demos cuenta de cada reacción de equilibrio que pueda afectar la solubilidad del precipitado. Por ejemplo, podemos determinar Ag ⁺ gravimétricamente añadiendo NaCl como precipitante, formando un precipitado de AgCl.

\[\mathrm{Ag}^{+}(a q)+\mathrm{Cl}^{-}(a q)\rightleftharpoons\mathrm{AgCl}(s) \label{8.1}\]

Si esta es la única reacción que consideramos, entonces predecimos que la solubilidad del precipitado, S _AgCl, viene dada por la siguiente ecuación.

\[S_{\mathrm{AgCl}}=\left[\mathrm{Ag}^{+}\right]=\frac{K_{\mathrm{sp}}}{\left[\mathrm{Cl}^{-}\right]} \label{8.2}\]

La ecuación\ ref {8.2} sugiere que podemos minimizar las pérdidas de solubilidad agregando un gran exceso de Cl ^—. De hecho, como se muestra en la Figura 8.2.1 , agregar un gran exceso de Cl ^— aumenta la solubilidad del precipitado.

Figura 8.2.1 . Solubilidad de AgCl en función de PCl. La línea roja discontinua muestra nuestra predicción para S _AgCl si asumimos incorrectamente que solo la reacción\ ref {8.1} y la ecuación\ ref {8.2} afectan la solubilidad del cloruro de plata. La curva azul sólida se calcula usando la Ecuación\ ref {8.7}, que da cuenta de la reacción\ ref {8.1} y las reacciones\ ref {8.3} —\ ref {8.5}. Debido a que la solubilidad de AgCl abarca varios órdenes de magnitud, S _AgCl se muestra en el eje y en forma logarítmica. Las líneas punteadas verticales son un diagrama de escalera para los complejos plata-cloro.

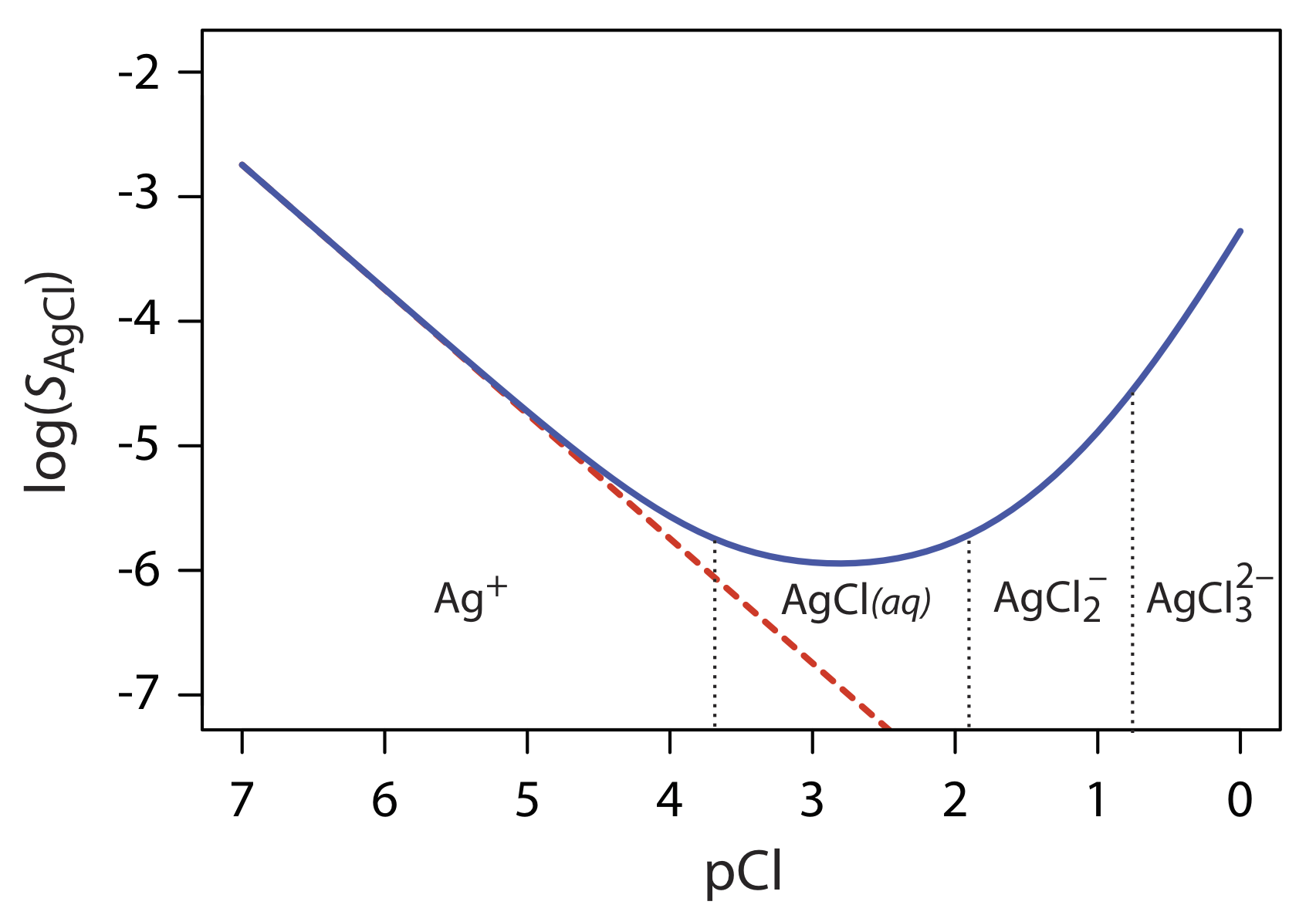
Para entender por qué la solubilidad de AgCl es más complicada que la relación sugerida por la Ecuación\ ref {8.2}, debemos recordar que Ag ⁺ también forma una serie de complejos solubles plata-cloro-metal—ligando.

\[\operatorname{Ag}^{+}(a q)+\mathrm{Cl}^{-}(a q)\rightleftharpoons\operatorname{AgCl}(a q) \quad \log K_{1}=3.70 \label{8.3}\]

\[\operatorname{AgCl}(a q)+\mathrm{Cl}^{-}(a q)\rightleftharpoons\operatorname{AgCl}_{2}(a q) \quad \log K_{2}=1.92 \label{8.4}\]

\[\mathrm{AgCl}_{2}^{-}(a q)+\mathrm{Cl}^{-}(a q)\rightleftharpoons\mathrm{AgCl}_{3}^{2-}(a q) \quad \log K_{3}=0.78 \label{8.5}\]

Obsérvese la diferencia entre la reacción\ ref {8.3}, en la que formamos AgCl (aq) como producto, y la reacción\ ref {8.1}, en la que formamos AgCl (s) como producto. La formación de AgCl (aq) a partir de AgCl (s)

\[\operatorname{AgCl}(s)\rightleftharpoons\operatorname{AgCl}(a q) \nonumber\]

se llama solubilidad intrínseca de AgCl.

La solubilidad real de AgCl es la suma de las concentraciones de equilibrio para todas las formas solubles de Ag ⁺.

\[S_{\mathrm{AgCl}}=\left[\mathrm{Ag}^{+}\right]+[\mathrm{AgCl}(a q)]+\left[\mathrm{AgCl}_{2}^-\right]+\left[\mathrm{AgCl}_{3}^{2-}\right] \label{8.6}\]

Al sustituir en la Ecuación\ ref {8.6} las expresiones constantes de equilibrio para reacción\ ref {8.1} y reacciones\ ref {8.3} —\ ref {8.5}, podemos definir la solubilidad de AgCl como

\[S_\text{AgCl} = \frac {K_\text{sp}} {[\text{Cl}^-]} + K_1K_\text{sp} + K_1K_2K_\text{sp}[\text{Cl}^-]+K_1K_2K_3K_\text{sp}[\text{Cl}^-]^2 \label{8.7}\]

La ecuación\ ref {8.7} explica la curva de solubilidad para AgCl mostrada en la Figura 8.2.1 . A medida que añadimos NaCl a una solución de Ag ⁺, la solubilidad de AgCl inicialmente disminuye debido a la reacción\ ref {8.1}. Bajo estas condiciones, los tres términos finales en la Ecuación\ ref {8.7} son pequeños y la Ecuación\ ref {8.2} es suficiente para describir la solubilidad de AgCl. Para mayores concentraciones de Cl ^—, la reacción\ ref {8.4} y la reacción\ ref {8.5} aumentan la solubilidad de AgCl. Claramente, la concentración de cloruro en equilibrio es importante si se desea determinar la concentración de plata precipitando AgCl. En particular, debemos evitar un gran exceso de cloruro.

Los complejos de plata-cloro predominantes para diferentes valores de PCl se muestran mediante el diagrama de escalera a lo largo del eje x en la Figura 8.2.1 . Obsérvese que el incremento en la solubilidad comienza cuando los complejos solubles de orden superior de\(\text{AgCl}_2^-\) y\(\text{AgCl}_3^{2-}\) son las especies predominantes.

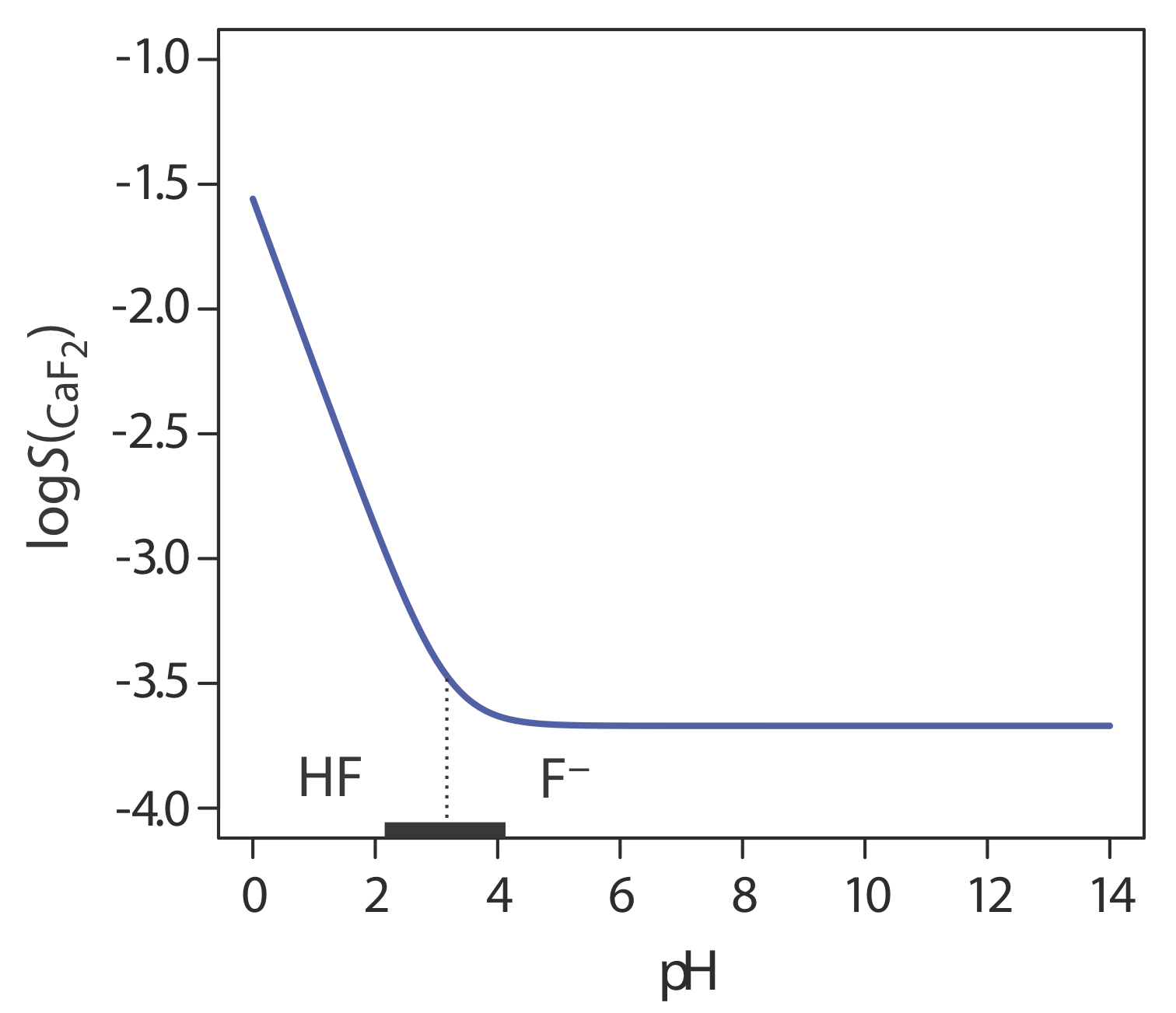
Otro parámetro importante que puede afectar la solubilidad de un precipitado es el pH. Por ejemplo, un precipitado de hidróxido, como Fe (OH) ₃, es más soluble a niveles de pH más bajos donde la concentración de OH ^— es pequeña. Debido a que el fluoruro es una base débil, la solubilidad del fluoruro de calcio\(S_{\text{CaF}_2}\), también es dependiente del pH. Podemos derivar una ecuación para\(S_{\text{CaF}_2}\) considerando las siguientes reacciones de equilibrio

\[\mathrm{CaF}_{2}(s)\rightleftharpoons \mathrm{Ca}^{2+}(a q)+2 \mathrm{F}^{-}(a q) \quad K_{\mathfrak{sp}}=3.9 \times 10^{-11} \label{8.8}\]

\[\mathrm{HF}(a q)+\mathrm{H}_{2} \mathrm{O}(l )\rightleftharpoons\mathrm{H}_{3} \mathrm{O}^{+}(a q)+\mathrm{F}^{-}(a q) \quad K_{\mathrm{a}}=6.8 \times 10^{-4} \label{8.9}\]

y la siguiente ecuación para la solubilidad de CaF ₂.

\[S_{\mathrm{Ca} \mathrm{F}_{2}}=\left[\mathrm{Ca}^{2+}\right]=\frac{1}{2}\left\{\left[\mathrm{F}^{-}\right]+[\mathrm{HF}]\right\} \label{8.10}\]

Asegúrate de que la Ecuación\ ref {8.10} tenga sentido para ti. Reacción\ ref {8.8} nos dice que la disolución de CaF ₂ produce un mol de Ca ^{2 +} por cada dos moles de F ^—, lo que explica el término de 1/2 en la Ecuación\ ref {8.10}. Debido a que F ^— es una base débil, debemos dar cuenta de ambas formas químicas en solución, lo que explica por qué incluimos HF.

Sustituir las expresiones constantes de equilibrio por reacción\ ref {8.8} y reacción\ ref {8.9} en Ecuación\ ref {8.10} nos permite definir la solubilidad de CaF ₂ en términos de la concentración de equilibrio de H ₃ O ⁺.

\[S_{\mathrm{CaF}_{2}}=\left[\mathrm{Ca}^{2+}\right]=\left\{\frac{K_{\mathrm{p}}}{4}\left(1+\frac{\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]}{K_{\mathrm{a}}}\right)^{2}\right\}^{1 / 3} \label{8.11}\]

La Figura 8.2.2 muestra cómo el pH afecta la solubilidad del CaF ₂. Dependiendo del pH de la solución, la forma predominante de fluoruro es HF o F ^—. Cuando el pH es mayor a 4.17, la especie predominante es F ^— y la solubilidad del CaF ₂ es independiente del pH porque solo la reacción\ ref {8.8} ocurre en una medida apreciable. A niveles de pH más ácidos, la solubilidad del CaF ₂ aumenta debido a la contribución de la reacción\ ref {8.9}.

Figura 8.2.2 . Solubilidad de CaF ₂ en función del pH. La curva azul sólida es una gráfica de la Ecuación\ ref {8.11}. La forma predominante de fluoruro en solución se muestra mediante el diagrama de escalera a lo largo del eje x, con el rectángulo negro indicando la región donde tanto HF como F ^— son especies importantes. Obsérvese que la solubilidad del CaF ₂ es independiente del pH para niveles de pH mayores a 4.17, y que su solubilidad aumenta dramáticamente a niveles de pH más bajos donde el HF es la especie predominante. Debido a que la solubilidad del CaF ₂ abarca varios órdenes de magnitud, su solubilidad se muestra en forma logarítmica.

Ejercicio 8.2.1

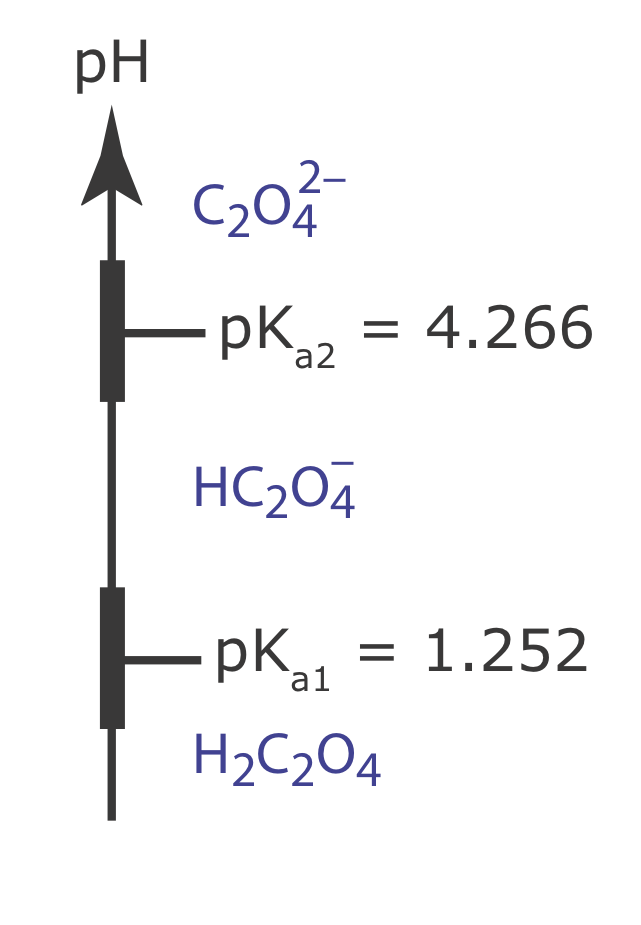
Puede usar un diagrama de escalera para predecir las condiciones que minimizarán la solubilidad de un precipitado. Dibuje un diagrama de escalera para el ácido oxálico, H ₂ C2O ₄, y utilícelo para predecir el rango de valores de pH que minimizarán la solubilidad de CaC ₂ O ₄. Constantes de equilibrio relevantes están en los apéndices.

Contestar

La reacción de solubilidad para CaC ₂ O ₄ es

\[\mathrm{CaC}_{2} \mathrm{O}_{4}(s)\rightleftharpoons \mathrm{Ca}^{2+}(a q)+\mathrm{C}_{2} \mathrm{O}_{4}^{2-}(a q) \nonumber\]

Para minimizar la solubilidad, el pH debe ser suficientemente básico para que el oxalato\(\text{C}_2\text{O}_4^{2-}\),, no reaccione para formar\(\text{HC}_2\text{O}_4^{-}\) o H ₂ C ₂ O ₄. A continuación se muestra el diagrama de escalera para el ácido oxálico, incluyendo rangos aproximados de tampón. Mantener un pH mayor a 5.3 asegura que\(\text{C}_2\text{O}_4^{2-}\) es la única forma importante de ácido oxálico en solución, minimizando la solubilidad del CaC ₂ O ₄.

Cuando la solubilidad es una preocupación, puede ser posible disminuir la solubilidad mediante el uso de un disolvente no acuoso. La solubilidad de un precipitado generalmente es mayor en una solución acuosa debido a la capacidad del agua para estabilizar iones a través de la solvatación. La peor capacidad de solvatación de un disolvente no acuoso, incluso aquellos que son polares, conduce a un producto de solubilidad más pequeño. Por ejemplo, la K _sp de PbSO ₄ está\(2 \times 10^{-8}\) en H ₂ O y\(2.6 \times 10^{-12}\) en una mezcla 50:50 de H ₂ O y etanol.

Evitar Impurezas

Además de tener una baja solubilidad, un precipitado debe estar libre de impurezas. Debido a que la precipitación suele ocurrir en una solución que es rica en sólidos disueltos, el precipitado inicial a menudo es impuro. Para evitar un error determinado, debemos eliminar estas impurezas antes de determinar la masa del precipitado.

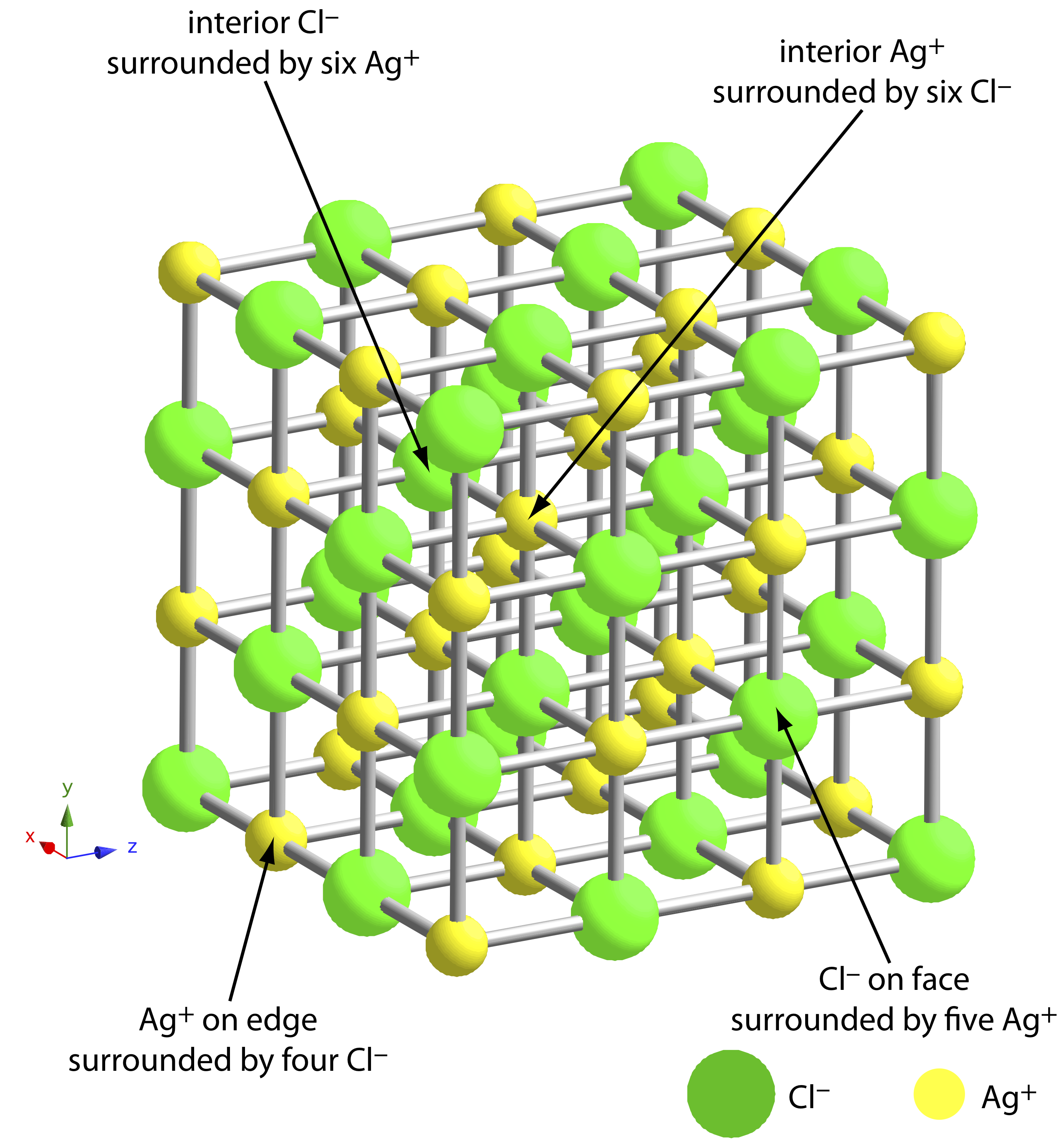
La mayor fuente de impurezas son las interacciones químicas y físicas que tienen lugar en la superficie del precipitado. Un precipitado generalmente es cristalino—aunque solo sea a escala microscópica— con una red bien definida de cationes y aniones. Esos cationes y aniones en la superficie del precipitado llevan, respectivamente, una carga positiva o negativa porque tienen esferas de coordinación incompletas. En un precipitado de AgCl, por ejemplo, cada ión de plata en el interior del precipitado está unido a seis iones cloruro. Un ion de plata en la superficie, sin embargo, está unido a no más de cinco iones cloruro y lleva una carga positiva parcial (Figura 8.2.3 ). La presencia de estas cargas parciales hace que la superficie del precipitado sea un sitio activo para las interacciones químicas y físicas que producen impurezas.

Figura 8.2.3 . Modelo de bola y varilla que muestra la estructura reticular de AgCl. Cada ion de plata en el interior de la red se une con seis iones cloruro y cada ion cloruro en el interior se une con seis iones de plata. Esos iones en la superficie o bordes de la red se unen a menos de seis iones y llevan una carga parcial. Un ion de plata en la superficie, por ejemplo, lleva una carga positiva parcial. Estas cargas hacen de la superficie de un precipitado un sitio activo para interacciones químicas y físicas.

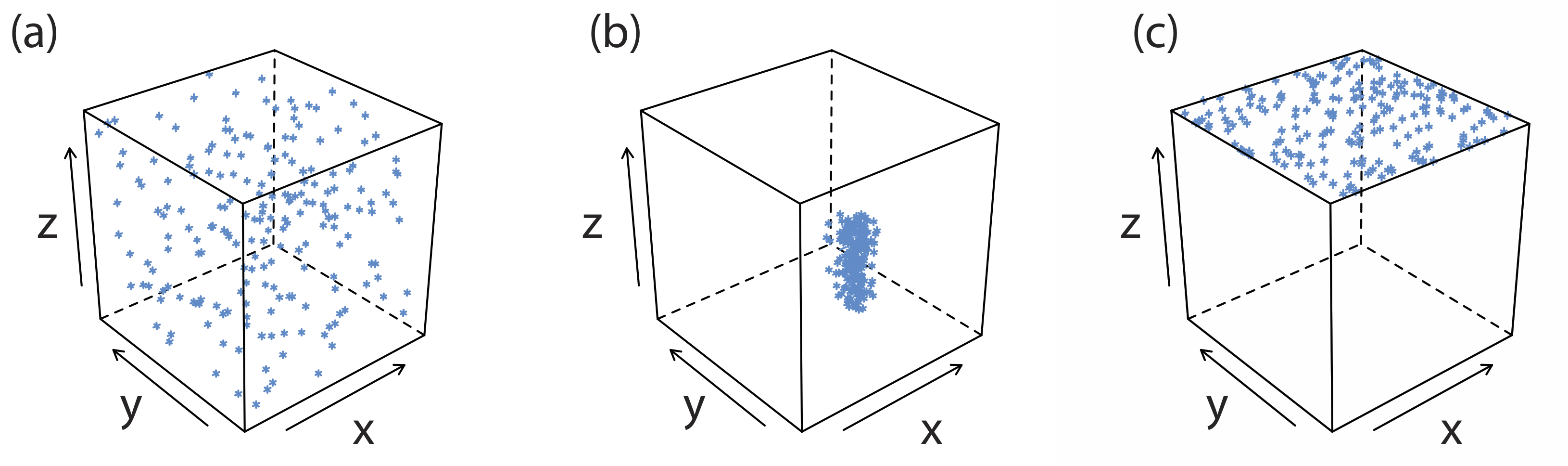
Una impureza común es una inclusión, en la que un interferente potencial, cuyo tamaño y carga es similar a un ion reticular, puede sustituirse en la estructura reticular si el interferente precipita con la misma estructura cristalina (Figura 8.2.4 a). La probabilidad de formar una inclusión es mayor cuando la concentración del ion interferente es sustancialmente mayor que la concentración del ion reticular. Una inclusión no disminuye la cantidad de analito que precipita, siempre que el precipitante esté presente en suficiente exceso. Así, la masa del precipitado siempre es mayor de lo esperado.

Figura 8.2.4 . Tres ejemplos de impurezas que se pueden formar durante la precipitación. El marco cúbico representa el precipitado y las marcas azules son impurezas presentes como (a) inclusiones, (b) oclusiones y (c) adsorbatos superficiales. Las inclusiones se distribuyen aleatoriamente por todo el precipitado. Las oclusiones se localizan dentro del interior del precipitado y los adsorbatos superficiales se localizan en el exterior del precipitado. Para facilitar la visualización, en (c) la adsorción se muestra en una sola superficie.

Una inclusión es difícil de eliminar ya que es químicamente parte de la red del precipitado. La única forma de eliminar una inclusión es a través de la reprecipitación en la que aislamos el precipitado de su solución sobrenadante, disolvemos el precipitado calentando en una pequeña porción de un disolvente adecuado, y luego reformamos el precipitado permitiendo que la solución se enfríe. Debido a que la concentración del interferente después de disolver el precipitado es menor que la de la solución original, la cantidad de material incluido disminuye tras la reprecipitación. Podemos repetir el proceso de reprecipitación hasta que la masa de la inclusión sea insignificante. La pérdida de analito durante la reprecipitación, sin embargo, es una fuente potencial de error determinado.

Supongamos que el 10% de un interferente forma una inclusión durante cada precipitación. Cuando inicialmente formamos el precipitado, el 10% del interferente original está presente como inclusión. Después de la primera reprecipitación, permanece 10% del interferente incluido, que es 1% del interferente original. Una segunda reprecipitación disminuye el interferente a 0.1% de la cantidad original.

Se forma una oclusión cuando un ion interferente queda atrapado dentro del precipitado en crecimiento. A diferencia de una inclusión, que se dispersa aleatoriamente dentro del precipitado, se localiza una oclusión, ya sea a lo largo de fallas dentro de la estructura reticular del precipitado o dentro de agregados de partículas de precipitado individuales (Figura 8.2.4 b). Una oclusión generalmente aumenta la masa de un precipitado; sin embargo, la masa del precipitado es menor si la oclusión incluye al analito en una forma de menor peso molecular que la del precipitado.

Podemos minimizar una oclusión manteniendo el precipitado en equilibrio con su solución sobrenadante durante un tiempo prolongado, un proceso llamado digestión. Durante una digestión, la naturaleza dinámica de los equilibrios solubilidad-precipitación, en los que el precipitado se disuelve y se reforma, asegura que la oclusión eventualmente se vuelva a exponer a la solución sobrenadante. Debido a que las tasas de disolución y reprecipitación son lentas, hay menos oportunidades de formar nuevas oclusiones.

Una vez completada la precipitación, la superficie continúa atrayendo iones de la solución (Figura 8.2.4 c). Estos adsorbatos superficiales comprenden un tercer tipo de impureza. Podemos minimizar la adsorción superficial disminuyendo la superficie disponible del precipitado. Un beneficio de la digestión es que aumenta el tamaño promedio de partícula de un precipitado. Debido a que la probabilidad de que una partícula se disuelva completamente es inversamente proporcional a su tamaño, durante la digestión las partículas más grandes aumentan de tamaño a expensas de las partículas más pequeñas. Una consecuencia de la formación de un menor número de partículas más grandes es una disminución general en la superficie del precipitado. También podemos eliminar los adsorbatos superficiales lavando el precipitado, aunque no podemos ignorar la pérdida potencial de analito.

Las inclusiones, oclusiones y adsorbatos superficiales son ejemplos de coprecipitados, especies solubles que se forman junto con el precipitado que contiene el analito. Otro tipo de impureza es un interferente que forma un precipitado independiente bajo las condiciones del análisis. Por ejemplo, la precipitación de dimetilglioxima de níquel requiere un pH ligeramente básico. Bajo estas condiciones cualquier Fe ^{3 +} en la muestra precipitará como Fe (OH) ₃. Además, debido a que la mayoría de los precipitantes rara vez son selectivos hacia un solo analito, existe el riesgo de que el precipitante reaccione tanto con el analito como con un interferente.

Además de formar un precipitado con Ni ^{2 +}, la dimetilglioxima también forma precipitados con Pd ^{2 +} y Pt ^{2 +}. Estos cationes son potenciales interferentes en un análisis de níquel.

Podemos minimizar la formación de precipitados adicionales controlando las condiciones de la solución. Si un interferente forma un precipitado que es menos soluble que el precipitado del analito, podemos precipitar el interferente y eliminarlo por filtración, dejando atrás el analito en solución. Alternativamente, podemos enmascarar el analito o el interferente para evitar su precipitación. Ambos enfoques descritos anteriormente se ilustran en el método analítico de Fresenius para la determinación de Ni en minerales que contienen Pb ^{2 +}, Cu ²⁺ y Fe ^{3 +} (ver Figura 1.1.1 en el Capítulo 1). Disolver el mineral en presencia de H ₂ SO ₄ precipita selectivamente Pb ^{2 +} como PbSO ₄. Al tratar el sobrenadante resultante con H ₂ S se precipita Cu ^{2 +} como CuS. Después de eliminar los CuS por filtración, se agrega amoníaco para precipitar Fe ^{3 +} como Fe (OH) ₃. El níquel, que forma un complejo de amina soluble, permanece en solución.

El enmascaramiento se introdujo en el Capítulo 7.

Controlar el tamaño de partícula

El tamaño importa a la hora de formar un precipitado. Las partículas más grandes son más fáciles de filtrar y, como se señaló anteriormente, una superficie más pequeña significa que hay menos oportunidades para que se formen adsorbatos superficiales. Controlando las condiciones de reacción podemos aumentar significativamente el tamaño promedio de partícula de un precipitado.

La formación de un precipitado consiste en dos eventos distintos: la nucleación, la formación inicial de partículas más pequeñas y estables del precipitado y el crecimiento de partículas. Las partículas más grandes se forman cuando la velocidad de crecimiento de las partículas excede la velocidad de nucleación. Comprender las condiciones que favorecen el crecimiento de las partículas es importante cuando diseñamos un método gravimétrico de análisis.

Definimos la supersaturación relativa de un soluto, RSS, como

\[R S S=\frac{Q-S}{S} \label{8.12}\]

donde Q es la concentración real del soluto y S es la concentración del soluto en equilibrio [Von Weimarn, P. P. Chem. Revs. 1925, 2, 217—242]. El numerador de la Ecuación\ ref {8.12}, Q — S, es una medida de la sobresaturación del soluto. Una solución con un gran valor positivo de RSS tiene una alta tasa de nucleación y produce un precipitado con muchas partículas pequeñas. Cuando el RSS es pequeño, es más probable que la precipitación ocurra por crecimiento de partículas que por nucleación.

Una solución supersaturada es aquella que contiene más soluto disuelto de lo que predice la química de equilibrio. Una solución supersaturada es inherentemente inestable y precipita soluto para alcanzar su posición de equilibrio. La rapidez con la que se produce la precipitación depende, en parte, del valor de RSS.

La ecuación\ ref {8.12} sugiere que podemos minimizar la RSS si disminuimos la concentración de soluto, Q, o si aumentamos la solubilidad del precipitado, S. La solubilidad de un precipitado generalmente aumenta a temperaturas más altas y ajustar el pH puede afectar la solubilidad de un precipitado si contiene un ion ácido o un ion básico. La temperatura y el pH, por lo tanto, son formas útiles de incrementar el valor de S. Formar el precipitado en una solución diluida de analito o agregar el precipitante lentamente y con agitación vigorosa son formas de disminuir el valor de Q.

Hay límites prácticos para minimizar RSS. Algunos precipitados, como Fe (OH) ₃ y PbS, son tan insolubles que S es muy pequeño y una RSS grande es inevitable. Tales solutos forman inevitablemente pequeñas partículas. Además, las condiciones que favorecen una RSS pequeña pueden llevar a una solución sobresaturada relativamente estable que requiere mucho tiempo para precipitar completamente. Por ejemplo, se requiere casi un mes para formar un precipitado visible de BasO ₄ en condiciones en las que el RSS inicial es 5 [Bassett, J.; Denney, R. C.; Jeffery, G. H. Mendham. J. Vogel's Textbook of Quantitative Inorganic Analysis, Longman: London, 4th Ed., 1981, p. 408].

Un precipitado visible tarda más en formarse cuando la RSS es pequeña tanto porque hay una velocidad lenta de nucleación como porque hay una disminución constante de la RSS a medida que se forma el precipitado. Una solución a este último problema es generar el precipitante in situ como producto de una reacción química lenta, que efectivamente mantiene una RSS constante. Debido a que el precipitado se forma en condiciones de baja RSS, la nucleación inicial produce un pequeño número de partículas. A medida que se forma precipitante adicional, el crecimiento de partículas reemplaza la nucleación, lo que resulta en partículas más grandes de precipitado. Este proceso se denomina precipitación homogénea [Gordon, L.; Salutsky, M. L.; Willard, H. H. Precipitación de Solución Homogénea, Wiley: NY, 1959].

Se utilizan dos métodos generales para la precipitación homogénea. Si la solubilidad del precipitado es dependiente del pH, entonces podemos mezclar el analito y el precipitante en condiciones donde no se produzca la precipitación, para luego aumentar o disminuir el pH generando químicamente OH ^— o H ₃ O ⁺. Por ejemplo, la hidrólisis de la urea, CO (NH ₂) ₂, es una fuente de OH ^—debido a las dos reacciones siguientes.

\[\mathrm{CO}\left(\mathrm{NH}_{2}\right)_{2}(a q)+\mathrm{H}_{2} \mathrm{O}( l)\rightleftharpoons2 \mathrm{NH}_{3}(a q)+\mathrm{CO}_{2}(g) \nonumber\]

\[\mathrm{NH}_{3}(a q)+\mathrm{H}_{2} \mathrm{O}( l)\rightleftharpoons\mathrm{OH}^{-}(a q)+\mathrm{NH}_{4}^{+}(a q) \nonumber\]

Debido a que la hidrólisis de la urea depende de la temperatura, la velocidad es insignificante a temperatura ambiente, podemos usar la temperatura para controlar la velocidad de hidrólisis y la velocidad de formación de precipitado. Por este método se han producido precipitados de CaC ₂ O ₄, por ejemplo. Después de disolver una muestra que contiene Ca ^{2 +}, la solución se acidifica con HCl antes de agregar una solución de 5% p/v (NH ₄) ₂ C ₂ O ₄. Debido a que la solución es ácida, no se forma un precipitado de CaC ₂ O ₄. La solución se calienta a aproximadamente 50 ^o C y se agrega urea. Después de varios minutos, comienza a formarse un precipitado de CaC ₂ O ₄, llegando a completarse la precipitación en aproximadamente 30 min.

En el segundo método de precipitación homogénea, el precipitante es generado por una reacción química. Por ejemplo, Pb ^{2 +} se precipita homogéneamente como PbCRo ₄ mediante el uso de bromato\(\text{BrO}_3^-\),, para oxidar Cr ^{3 +} a\(\text{CrO}_4^{2-}\).

\[6 \mathrm{BrO}_{3}^{-}(a q)+10 \mathrm{Cr}^{3+}(a q)+22 \mathrm{H}_{2} \mathrm{O}(l)\rightleftharpoons 3 \mathrm{Br}_{2}(a q)+10 \mathrm{CrO}_{4}^{2-}(a q)+44 \mathrm{H}^{+}(a q) \nonumber\]

La Figura 8.2.5 muestra el resultado de la preparación de PbCRo ₄ por adición directa de K ₂ CrO ₄ (Vaso A) y por precipitación homogénea (Vaso B). Ambos vasos contienen la misma cantidad de PbCRo ₄. Debido a que la adición directa de K ₂ CrO ₄ conduce a una precipitación rápida y a la formación de partículas más pequeñas, el precipitado permanece menos sedimentado que el precipitado preparado homogéneamente. Obsérvese, también, la diferencia en el color de los dos precipitados.

Figura 8.2.5 . Dos precipitados de PbCRo ₄. En el vaso de precipitados A, la mezcla de 0.1 M Pb (NO ₃) ₂ y 0.1 M K ₂ CrO ₄ forma el precipitado en condiciones de alta RSS. El precipitado se forma rápidamente y consiste en partículas muy pequeñas. En el vaso B, al calentar una solución de 0.1 M Pb (NO ₃) ₂, 0.1 M Cr (NO ₃) ₃ y 0.1 M KBro ₃ se oxida lentamente Cr ^{3 +} a\(\text{CrO}_4^{2-}\), precipitando PbCRo ₄ en condiciones de baja RSS. El precipitado se forma lentamente y consiste en partículas mucho más grandes.

El efecto del tamaño de partícula sobre el color es bien conocido por los geólogos, quienes utilizan una prueba de rayas para ayudar a identificar minerales. El color de un mineral a granel y su color cuando está en polvo a menudo son diferentes. Frotar un mineral a través de un plato de porcelana sin glasear deja atrás una pequeña veta del mineral en polvo. Las muestras a granel de hematita, Fe ₂ O ₃, son de color negro, pero su veta es de un rojo oxidado familiar. La crocita, el mineral PbCRo ₄, es de color rojo anaranjado; su veta es naranja-amarilla.

Una precipitación homogénea produce grandes partículas de precipitado que están relativamente libres de impurezas. Estas ventajas, sin embargo, se compensan por el aumento del tiempo necesario para producir el precipitado y por la tendencia de que el precipitado se deposite como una película delgada en las paredes del recipiente. Este último problema es particularmente grave para los precipitados de hidróxido generados con urea.

Un método adicional para aumentar el tamaño de partícula merece mención. Cuando las partículas de un precipitado son eléctricamente neutras, tienden a coagularse en partículas más grandes que son más fáciles de filtrar. La adsorción superficial del exceso de iones reticulares, sin embargo, proporciona a las partículas del precipitado una carga superficial neta positiva o negativa neta. La repulsión electrostática entre partículas de carga similar evita que se coagulen en partículas más grandes.

Vamos a utilizar la precipitación de AgCl a partir de una solución de AgnO ₃ usando NaCl como precipitante para ilustrar este efecto. Al principio de la precipitación, cuando el NaCl es el reactivo limitante, los iones Ag ⁺ en exceso se adsorben químicamente a las partículas de AgCl, formando una capa de adsorción primaria cargada positivamente (Figura 8.2.6 a). La solución en contacto con esta capa contiene más aniones inertes,\(\text{NO}_3^-\) en este caso, que cationes inertes, Na ⁺, dando una capa de adsorción secundaria con una carga negativa que equilibra la carga positiva de la capa de adsorción primaria. La solución fuera de la capa de adsorción secundaria permanece eléctricamente neutra. La coagulación no puede ocurrir si la capa de adsorción secundaria es demasiado gruesa porque las partículas individuales de AgCl son incapaces de acercarse entre sí lo suficientemente cerca.

Figura 8.2.6 . Dos métodos para coagular un precipitado de AgCl. (a) La coagulación no ocurre debido a la repulsión electrostática entre las partículas cargadas positivamente. (b) Disminuir la carga dentro de la capa primaria de adsorción, mediante la adición de NaCl adicional, disminuye la repulsión electrostática y permite que las partículas se coagulen. (c) La adición de iones inertes adicionales disminuye el espesor de la capa secundaria de adsorción. Debido a que las partículas pueden acercarse entre sí más de cerca, son capaces de coagular.

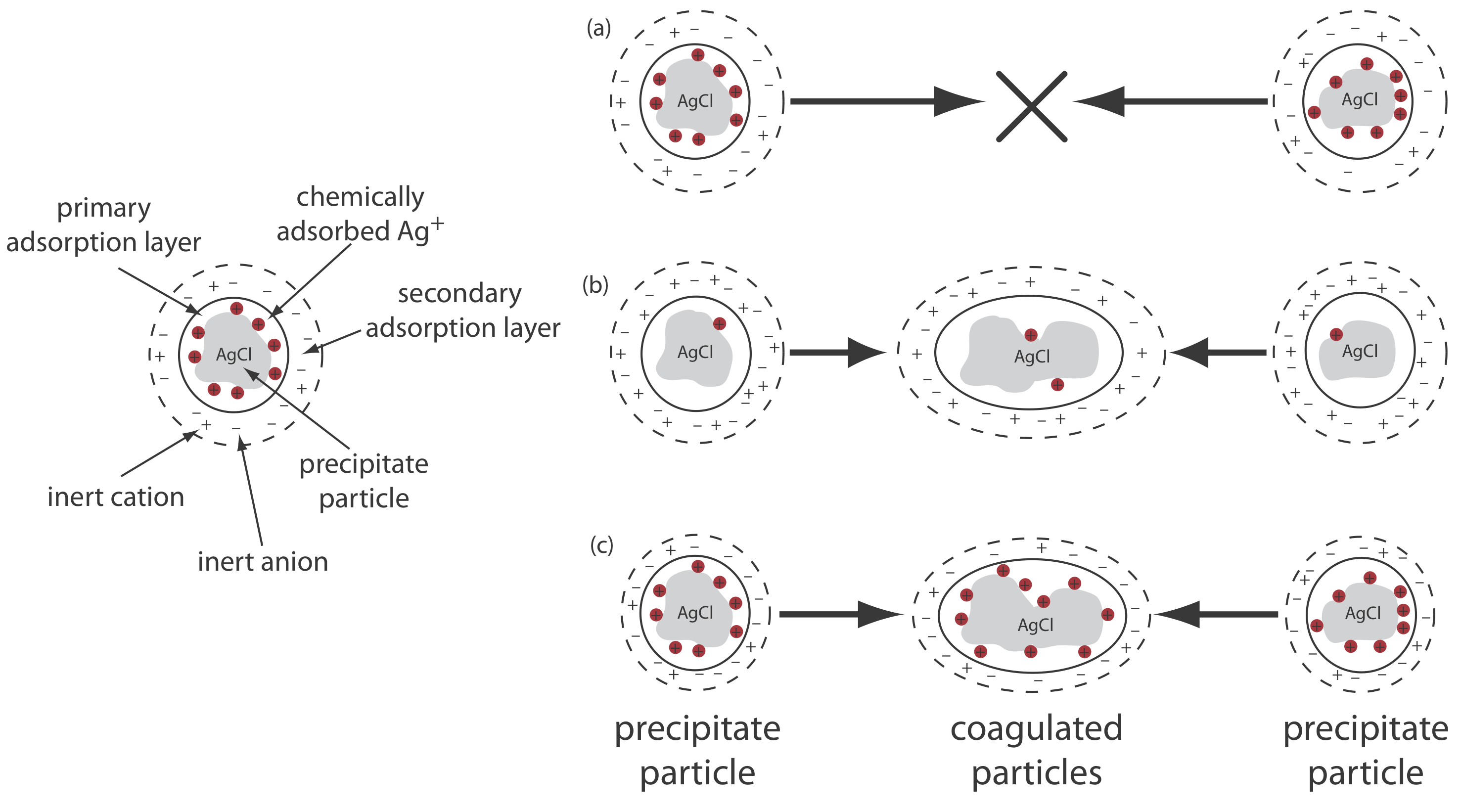
Podemos inducir la coagulación de tres maneras: disminuyendo el número de iones Ag ⁺ químicamente adsorbidos, aumentando la concentración de iones inertes, o calentando la solución. A medida que agregamos NaCl adicional, precipitando más del exceso de Ag ⁺, disminuye el número de iones de plata químicamente adsorbidos y se produce coagulación (Figura 8.2.6 b). ^{Sin embargo, agregar demasiado NaCl crea una capa de adsorción primaria de exceso de Cl, con una pérdida de coagulación.}

La coagulación y descoagulación de AgCl a medida que añadimos NaCl a una solución de AgnO ₃ puede servir como punto final para una valoración. Consulte el Capítulo 9 para obtener detalles adicionales.

Una segunda forma de inducir la coagulación es agregar un electrolito inerte, lo que aumenta la concentración de iones en la capa de adsorción secundaria (Figura 8.2.6 c). Con más iones disponibles, el espesor de la capa de absorción secundaria disminuye. Las partículas de precipitado ahora pueden acercarse entre sí más estrechamente, lo que permite que el precipitado se coagule. La cantidad de electrolito necesaria para provocar la coagulación espontánea se denomina concentración crítica de coagulación.

El calentamiento de la solución y el precipitado proporciona una tercera forma de inducir la coagulación. A medida que aumenta la temperatura, disminuye el número de iones en la capa de adsorción primaria, lo que disminuye la carga superficial del precipitado. Además, el calentamiento aumenta la energía cinética de las partículas, permitiéndoles superar la repulsión electrostática que impide la coagulación a temperaturas más bajas.

Filtrando el precipitado

Después de precipitar y digerir un precipitado, lo separamos de la solución filtrando. El método de filtración más común utiliza papel de filtro, el cual se clasifica de acuerdo a su velocidad, su tamaño y su contenido de cenizas en la ignición. La velocidad, o la rapidez con la que el sobrenadante pasa a través del papel de filtro, es una función del tamaño de poro del papel. Un tamaño de poro mayor permite que el sobrenadante pase más rápidamente a través del papel de filtro, pero no retiene pequeñas partículas de precipitado. El papel de filtro se clasifica como rápido (retiene partículas mayores de 20—25 μm), medio-rápido (retiene partículas mayores de 16 μm), medio (retiene partículas mayores de 8 μm) y lento (retiene partículas mayores de 2—3 μm). La elección adecuada de la velocidad de filtrado es importante. Si la velocidad de filtrado es demasiado rápida, es posible que no podamos retener parte del precipitado, lo que provoca un error determinado negativo. Por otro lado, el precipitado puede obstruir los poros si utilizamos un papel de filtro que es demasiado lento.

El tamaño de un papel de filtro es solo su diámetro. El papel de filtro viene en muchos tamaños, incluyendo 4.25 cm, 7.0 cm, 11.0 cm, 12.5 cm, 15.0 cm y 27.0 cm. Elige una talla que se ajuste cómodamente a tu embudo. Para un embudo típico de tallo largo de 65 mm, el papel de filtro de 11.0 cm y 12.5 cm son buenas opciones.

Debido a que el papel de filtro es higroscópico, no es fácil secarlo a un peso constante. Cuando la precisión es importante, el papel de filtro se retira antes de determinar la masa del precipitado. Después de transferir el precipitado y el papel de filtro a un crisol cubierto, calentamos el crisol a una temperatura que cubre el papel a CO ₂ (g) y H ₂ O (g), un proceso llamado ignición.

La ignición de un papel de filtro de mala calidad deja un residuo de ceniza inorgánica. Para el trabajo cuantitativo, use un papel de filtro bajo en cenizas. Este grado de papel de filtro se pretrata con una mezcla de HCl y HF para eliminar los materiales inorgánicos. El papel de filtro cuantitativo típicamente tiene un contenido de cenizas de menos de 0.010% p/p.

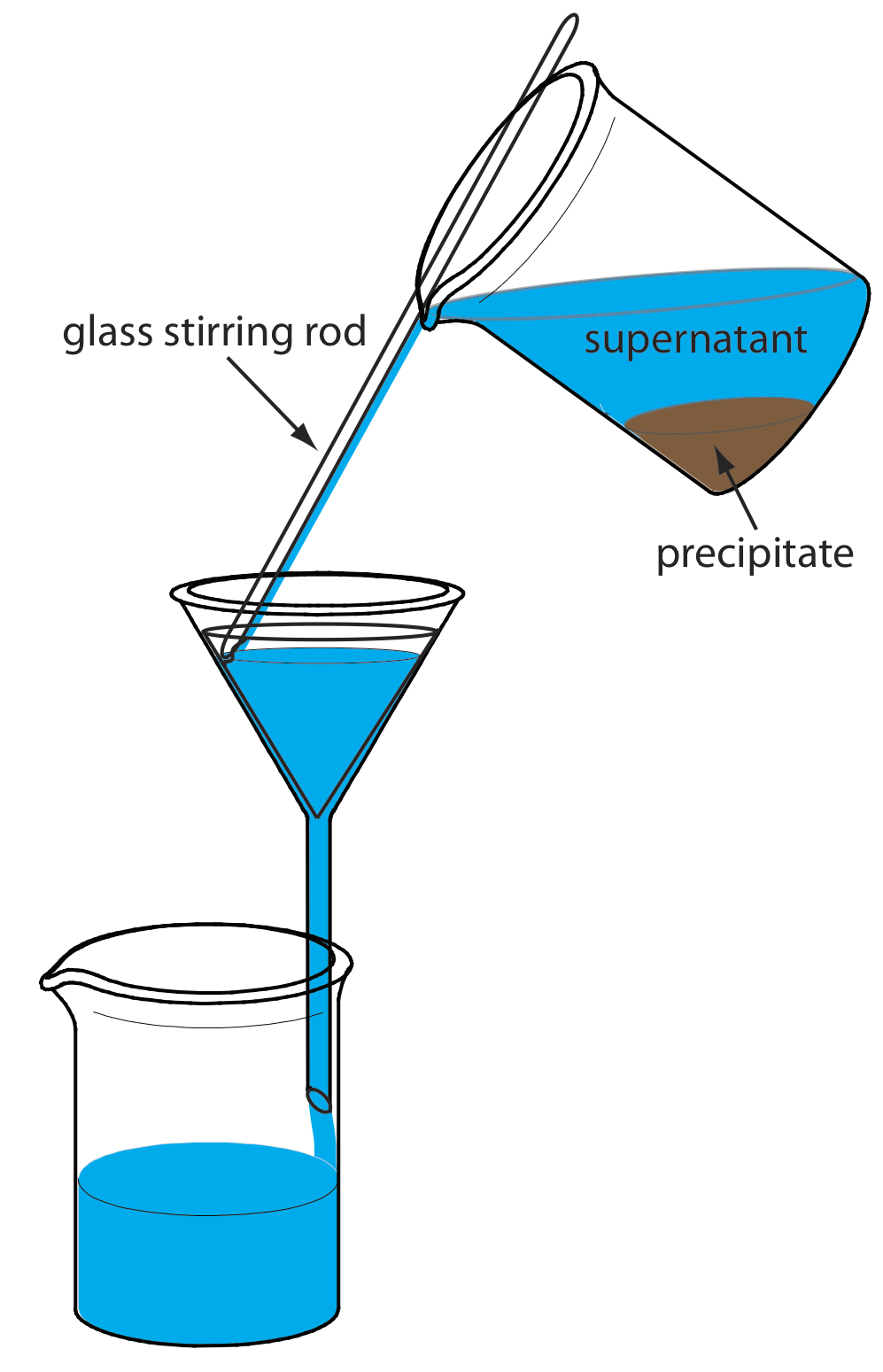
La filtración por gravedad se logra plegando el papel de filtro en un cono y colocándolo en un embudo de tallo largo (Figura 8.2.7 ). Para formar un sello hermético entre el cono del filtro y el embudo, humedecemos el papel con agua o sobrenadante y presionamos el papel contra la pared del embudo. Cuando se prepara adecuadamente, el tallo del embudo se llena con el sobrenadante, aumentando la velocidad de filtración.

Figura 8.2.7 . Para preparar un cono de papel de filtro, el círculo de papel de filtro se (a) dobla por la mitad (b), se dobla en media segunda vez (c), se parte (d) y se arranca una pequeña
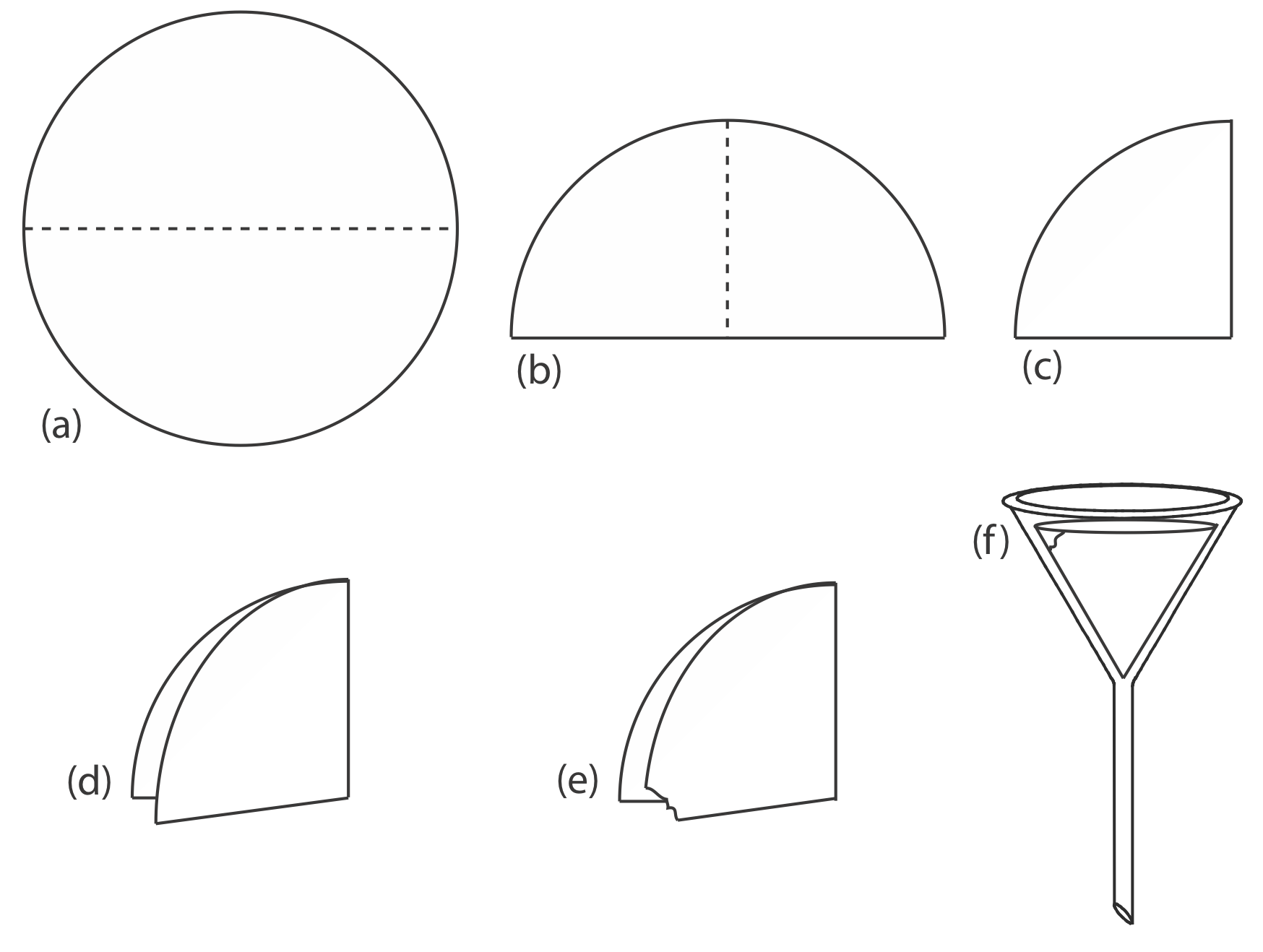
esquina (e) antes de que el papel se abra en un cono y se coloque en el embudo (f).

El precipitado se transfiere al filtro en varias etapas. El primer paso es decantar la mayor parte del sobrenadante a través del papel de filtro sin transferir el precipitado (Figura 8.2.8 ). Esto evita que el papel de filtro se obstruya al inicio del proceso de filtración. El precipitado se enjuaga mientras permanece en su vaso de precipitados, con los enjuagues decantados a través del papel de filtro. Finalmente, el precipitado se transfiere al papel de filtro usando una corriente de solución de enjuague. Cualquier precipitado que se aferre a las paredes del vaso de precipitados se transfiere utilizando un policía de goma (una espátula de goma flexible unida al extremo de una varilla agitadora de vidrio).

Figura 8.2.8 . Procedimiento adecuado para transferir el sobrenadante al cono de papel de filtro. La varilla de agitación de vidrio permite que el sobrenadante se filtre en el embudo sin salpicar.

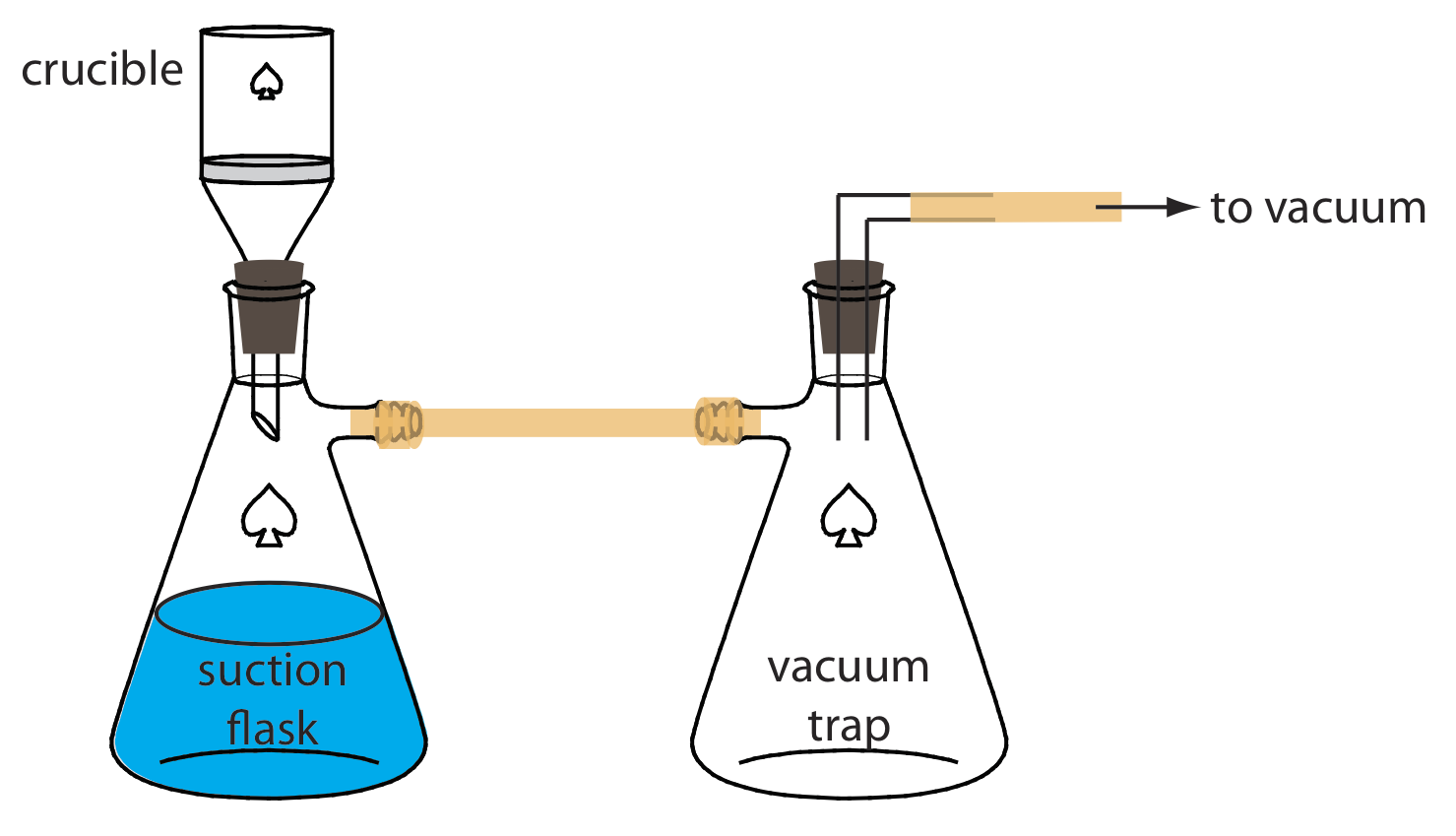
Un método alternativo para filtrar un precipitado es usar un crisol filtrante. La opción más común es un crisol de vidrio fritado que contiene un filtro de disco de vidrio poroso. Los crisoles de vidrio fritado se clasifican por su porosidad: gruesos (partículas de retención mayores de 40—60 μm), medios (partículas de retención mayores de 10—15 μm) y finos (partículas de retención mayores de 4—5.5 μm). Otro tipo de crisol filtrante es el crisol Gooch, que es un crisol de porcelana con fondo perforado. Se coloca una estera de fibra de vidrio en el crisol para retener el precipitado. Para ambos tipos de crisoles, el pre- cipitado se transfiere de la misma manera descrita anteriormente para papel de filtro. En lugar de usar la gravedad, el sobrenadante se extrae a través del crisol con la ayuda de succión de un aspirador o bomba de vacío (Figura 8.2.9 ).

Figura 8.2.9 . Procedimiento para filtrar un precipitado a través de un crisol filtrante. La trampa evita que el agua del aspirador se vuelva a lavar en el matraz de succión.

Enjuague del precipitado

Debido a que el sobrenadante es rico en iones inertes disueltos, debemos eliminar las trazas residuales de sobrenadante sin incurrir en pérdida de analito debido a la solubilidad. En muchos casos esto simplemente implica el uso de solventes fríos o soluciones de enjuague que contienen solventes orgánicos como el etanol. El pH de la solución de enjuague es crítico si el precipitado contiene un ión ácido o básico. Cuando la coagulación juega un papel importante en la determinación del tamaño de partícula, agregar un electrolito inerte volátil a la solución de enjuague evita que el precipitado vuelva a partículas más pequeñas que podrían pasar a través del filtro. Este proceso de revertir a partículas más pequeñas se llama peptización. El electrolito volátil se elimina al secar el precipitado.

En general, podemos minimizar la pérdida de analito si utilizamos varias porciones pequeñas de solución de enjuague en lugar de un solo volumen grande. Probar la solución de enjuague usada para detectar la presencia de una impureza es otra manera de proteger contra el enjuague excesivo del precipitado. Por ejemplo, si Cl ^— es un ion residual en el sobrenadante, podemos probar su presencia usando AgnO ₃. Después de recolectar una pequeña porción de la solución de enjuague, agregamos unas gotas de AgnO ₃ y buscamos la presencia o ausencia de un precipitado de AgCl. Si se forma un precipitado, entonces sabemos que Cl ^— está presente y continuar enjuagando el precipitado. No se necesita aclarado adicional si el _{AgnO 3} no produce un precipitado.

Secar el precipitado

Después de separar el precipitado de su solución sobrenadante, secamos el precipitado para eliminar trazas residuales de solución de enjuague y eliminar cualquier impureza volátil. La temperatura y el método de secado dependen del método de filtración y de la forma química deseada del precipitado. Colocar el precipitado en un horno de laboratorio y calentar a una temperatura de 110 ^o C es suficiente para eliminar el agua y otras impurezas fácilmente volatilizadas. Las temperaturas más altas requieren un horno de mufla, un quemador Bunsen o un quemador Meker, y son necesarios si necesitamos descomponer el precipitado antes de determinar su peso.

Debido a que el papel de filtro absorbe la humedad, debemos retirarla antes de pesar el precipitado. Esto se logra plegando el papel de filtro sobre el precipitado y transfiriendo tanto el papel de filtro como el precipitado a un crisol de porcelana o platino. El calentamiento suave primero seca y luego carboniza el papel de filtro. Una vez que el papel comienza a calcinarse, aumentamos lentamente la temperatura hasta que no hay rastro del papel de filtro y cualquier carbono restante se oxida a CO ₂.

Los crisoles de vidrio fritado no pueden soportar altas temperaturas y se secan en un horno a una temperatura inferior a 200 ^o C. Las esteras de fibra de vidrio utilizadas en los crisoles Gooch se pueden calentar a una temperatura máxima de aproximadamente 500 ^o C.

Composición del precipitado final

Para una aplicación cuantitativa, el precipitado final debe tener una composición bien definida. Un precipitado que contiene iones volátiles o cantidades sustanciales de agua hidratada, generalmente se seca a una temperatura que elimina completamente estas especies volátiles. Por ejemplo, un método gravimétrico estándar para la determinación del magnesio implica su precipitación como MGnH ₄ PO ₄ •6H ₂ O. Desafortunadamente, este precipitado es difícil de secar a temperaturas más bajas sin perder una cantidad inconsistente de agua hidratada y amoníaco. En cambio, el precipitado se seca a una temperatura mayor a 1000 ^o C donde se descompone en pirofosfato de magnesio, Mg ₂ P ₂ O ₇.

Se encuentra un problema adicional si el sólido aislado no es estequiométrico. Por ejemplo, precipitar Mn ^{2 +} como Mn (OH) ₂ y calentar frecuentemente produce un óxido de manganeso no estequiométrico, _{MnO x}, donde x varía entre uno y dos. En este caso el producto no estequiométrico es el resultado de formar una mezcla de óxidos con diferente estado de oxidación del manganeso. Otros compuestos no estequiométricos se forman como resultado de defectos reticulares en la estructura cristalina [Ward, R., ed., Non-Stoichiometric Compound (Ad. Chem. Ser. 39), American Chemical Society: Washington, D. C., 1963].

Método Representativo 8.2.1: Determinación de Mg en Agua y Aguas Residuales

La mejor manera de apreciar los detalles teóricos y prácticos discutidos en esta sección es examinar cuidadosamente un método gravimétrico típico de precipitación. Aunque cada método es único, la determinación de Mg ^{2 +} en agua y aguas residuales precipitando MgNh ₄ PO ₄ • 6H ₂ O y aislando Mg _{2 P 2} O ₇ proporciona un ejemplo instructivo de un procedimiento típico. La descripción aquí se basa en el Método 3500-Mg D en Métodos Estándar para el Examen de Agua y Aguas Residuales, 19a Ed., American Public Health Asso- ciation: Washington, D. C., 1995. Con la publicación de la vigésima edición en 1998, este método ya no aparece catalogado como un método aprobado.

Descripción del método

El magnesio se precipita como MgNH _{4 PO 4} •6H ₂ O usando (NH ₄) ₂ HPO ₄ como precipitante. La solubilidad del precipitado en una solución neutra es relativamente alta (0.0065 g/100 mL en agua pura a 10 ^o C), pero es mucho menos soluble en presencia de amoníaco diluido (0.0003 g/100 mL en 0.6 M NH ₃). Debido a que el precipitante no es selectivo, es necesaria una separación preliminar de Mg ^{2 +} de los potenciales interferentes. El calcio, que es el interferente más significativo, se elimina precipitándolo como CaC ₂ O ₄. La presencia de exceso de sales de amonio del precipitante, o de la adición de demasiado amoníaco, conduce a la formación de Mg (NH ₄) ₄ (PO ₄) ₂, que forma Mg (PO ₃) ₂ después del secado. El precipitado se aísla por filtración por gravedad, utilizando una solución de enjuague de amoníaco diluido. Después de filtrar, el precipitado se convierte en Mg ₂ P ₂ O ₇ y se pesa.

Procedimiento

Transfiera una muestra que no contenga más de 60 mg de Mg ^{2 +} a un vaso de precipitados de 600 ml. Agrega 2—3 gotas de indicador rojo de metilo y, si es necesario, ajusta el volumen a 150 mL. Acidificar la solución con HCl 6 M y agregar 10 mL de 30% p/v (NH ₄) ₂ HPO ₄. Después de enfriar y con agitación constante, agregar NH ₃ concentrado gota a gota hasta que el indicador rojo metilo se vuelva amarillo (pH > 6.3). Después de agitar durante 5 min, agregar 5 mL de NH ₃ concentrado y continuar agitando por 10 min adicionales. Dejar reposar la solución resultante y precipitar durante la noche. Aislar el precipitado filtrando a través de papel de filtro, enjuagando con 5% v/v NH ₃. Disolver el precipitado en 50 mL de HCl al 10% v/v y precipitar por segunda vez siguiendo el mismo procedimiento. Después de filtrar, retire con cuidado el papel de filtro carbonizando. Calentar el precipitado a 500 ^o C hasta que el residuo sea blanco, y luego llevar el precipitado a peso constante a 1100 ^o C.

Preguntas

1. ¿Por qué el procedimiento requiere una muestra que no contenga más de 60 mg de Mg ^{2 +}?

Una porción de 60 mg de Mg ^{2 +} genera aproximadamente 600 mg de MgNH _{4 PO 4} •6H ₂ O, que es una cantidad sustancial de precipitado. Una mayor cantidad de precipitado es difícil de filtrar y difícil de enjuagar libre de impurezas.

2. ¿Por qué la solución se acidifica con HCl antes de agregar el precipitante?

El HCl asegura que MgNH ₄ PO ₄ • 6H ₂ O no precipite inmediatamente después de agregar el precipitante. Debido a que\(\text{PO}_4^{3-}\) es una base débil, el precipitado es soluble en una solución fuertemente ácida. Si agregamos el precipitante en condiciones neutras o básicas (es decir, una RSS alta), entonces el precipitado resultante consistirá en partículas más pequeñas y menos puras. El aumento del pH mediante la adición de base permite que el precipitado se forme en condiciones más favorables (es decir, una baja RSS).

3. ¿Por qué se agrega a la solución el indicador ácido-base rojo de metilo?

El indicador cambia de color a un pH de aproximadamente 6.3, lo que indica que hay suficiente NH ₃ para neutralizar el HCl agregado al inicio del procedimiento. La cantidad de NH ₃ es crucial para este procedimiento. Si agregamos NH ₃ insuficiente, entonces la solución es demasiado ácida, lo que aumenta la solubilidad del precipitado y conduce a un error negativo determinado. Si añadimos demasiado NH ₃, el precipitado puede contener trazas de Mg (NH ₄) ₄ (PO ₄) ₂, que al secarse, forma Mg (PO ₃) ₂ en lugar de Mg ₂ P ₂ O ₇. Esto aumenta la masa del precipitado encendido, y da un error determinado positivo. Después de agregar suficiente NH ₃ para neutralizar el HCl, agregamos 5 mL adicionales de NH ₃ para completar la precipitación cuantitativa de MgNH ₄ PO ₄ • 6H ₂ O.

4. _{Explicar por qué la formación de Mg (PO 3) 2 en lugar de Mg 2 P 2 O 7 aumenta la masa del precipitado.}

Cada mol de Mg ₂ P ₂ O ₇ contiene dos moles de magnesio y cada mol de Mg (PO ₃) ₂ contiene solo un mol de magnesio. Una conservación de la masa, por lo tanto, requiere que se formen dos moles de Mg (PO ₃) ₂ en lugar de cada mol de Mg ₂ P ₂ O ₇. Un mol de Mg ₂ P ₂ O ₇ pesa 222.6 g. Dos moles de Mg (PO ₃) ₂ pesan 364.5 g. Cualquier reemplazo de Mg ₂ P ₂ O ₇ por Mg (PO ₃) ₂ debe aumentar la masa del precipitado.

5. ¿Qué pasos adicionales, más allá de los discutidos en las preguntas 2 y 3, ayudan a mejorar la pureza del precipitado?

Dos pasos adicionales en el procedimiento ayudan a formar un precipitado que está libre de impurezas: digestión y reprecipitación.

6. ¿Por qué se enjuaga el precipitado con una solución de NH ₃ al 5% v/v?

Esto se hace por la misma razón que la precipitación se realiza en una solución amoniacal; el uso de amoníaco diluido minimiza las pérdidas de solubilidad cuando enjuagamos el precipitado.

Aplicaciones Cuantitativas

Aunque ya no es una técnica analítica común, la gravimetría de precipitación aún proporciona un enfoque confiable para evaluar la precisión de otros métodos de análisis, o para verificar la composición de materiales de referencia estándar. En esta sección se revisa la aplicación general de la gravimetría de precipitación al análisis de compuestos inorgánicos y orgánicos.

Análisis Inorgánico

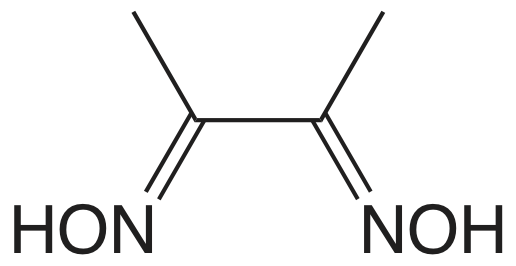
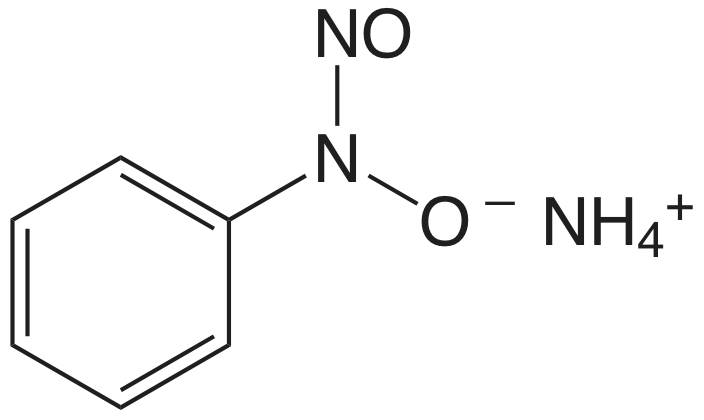
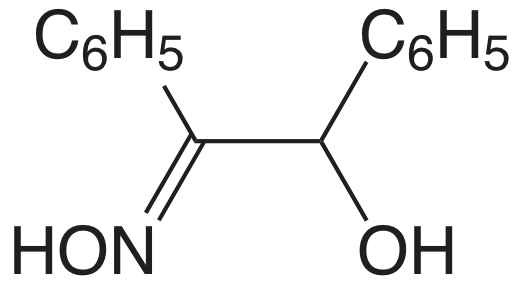
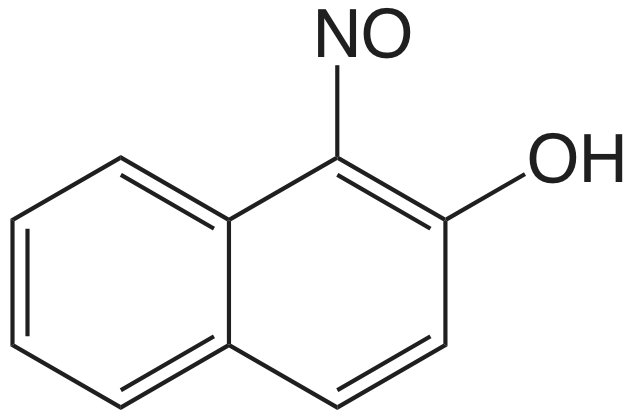
El cuadro 8.2.1 proporciona un resumen de los métodos gravimétricos de precipitación para cationes y aniones inorgánicos. Varios métodos para la generación homogénea de precipitantes se muestran en la Tabla 8.2.2 . La mayoría de los precipitantes inorgánicos muestran poca selectividad para el analito. Muchos precipitantes orgánicos, sin embargo, son selectivos para uno o dos iones inorgánicos. En el cuadro 8.2.3 se enumeran ejemplos de varios precipitantes orgánicos comunes.

Tabla 8.2.1 . Métodos Gravimétricos de Precipitación Seleccionados para Cationes y Aniones Inorgánicos (Dispuestos por Precipitante)

analito	precipitante	precipitado formado	precipitado pesado
Ba ^2 ^+	(NH 4) 2 CRo 4	Bacro 4	Bacro 4
Pb ^2 ^+	K 2 CrO 4	PbCRo 4	PbCRo 4
Ag ^+	HCl	AgCl	AgCl
\(\text{Hg}_2^{2+}\)	HCl	Hg 2 Cl 2	Hg 2 Cl 2
Al ^3 ^+	NH 3	Al (OH) 3	Al 2 O 3
Ser ^2+	NH 3	Ser (OH) 2	BeO
Fe ^3 ^+	NH 3	Fe (OH) 3	Fe 2 O 3
Ca ^2+	(NH 4) 2 CRo 4	CaC 2 O 4	CaCo 3 o CaO
Sb ^3 ^+	H 2 S	Sb 2 S 3	Sb 2 S 3
Como ^3 ^+	H 2 S	Como 2 S 3	Como 2 S 3
Hg ^2+	H 2 S	HgS	HgS
Ba ^2+	H 2 SO 4	BasO 4	BasO 4
Pb ^2+	H 2 SO 4	PbSO 4	PbSO4
Sr ^2+	H 2 SO 4	SRSO 4	SRSO 4
Ser ^3 ^+	(NH 4) 2 HPO 4	NH 4 BePo 4	Ser 2 P 2 O 7
Mg ^2+	(NH 4) 2 HPO 4	NH 4 MgPO 4	Mg 2 P 2 O 7
Zn ^2+	(NH 4) 2 HPO 4	NH 4 ZnPO 4	Zn 2 P 2 O 7
Sr ^2+	KH 2 PO 4	SrHPO 4	Sr 2 P 2 O 7
CN ^—	AgnO 3	AgCn	AgCn
I-	AgnO 3	AGi	AGi
Br ^—	AgnO 3	AgBr	AgBr
Cl ^—	AgnO 3	AgCl	AgCl
\(\text{ClO}_3^-\)	FESO 4 /AgnO 3	AgCl	AgCl
SCN ^—	SO 2 /CuSO 4	CUSCN	CUSCN
\(\text{SO}_4^2-\)	BacL 2	BasO 4	BasO 4

Tabla 8.2.2 . Reacciones para la preparación homogénea de precipitantes inorgánicos seleccionados

precipitante	reacción
OH—	\(\left(\mathrm{NH}_{2}\right)_{2} \mathrm{CO}(a q)+3 \mathrm{H}_{2} \mathrm{O}(l)\rightleftharpoons2 \mathrm{NH}_{4}^{+}(a q)+\mathrm{CO}_{2}(g)+2 \mathrm{OH}^{-}(a q)\)
\(\text{SO}_4^{2-}\)	\(\mathrm{NH}_{2} \mathrm{HSO}_{3}(a q)+2 \mathrm{H}_{2} \mathrm{O}(l )\rightleftharpoons\mathrm{NH}_{4}^{+}(a q)+\mathrm{H}_{3} \mathrm{O}^{+}(a q)+\mathrm{SO}_{4}^{2-}(a q)\)
S ^2—	\(\mathrm{CH}_{3} \mathrm{CSNH}_{2}(a q)+\mathrm{H}_{2} \mathrm{O}(l )\rightleftharpoons\mathrm{CH}_{3} \mathrm{CONH}_{2}(a q)+\mathrm{H}_{2} \mathrm{S}(a q)\)
\(\text{IO}_3^-\)	\(\mathrm{HOCH}_{2} \mathrm{CH}_{2} \mathrm{OH}(a q)+\mathrm{IO}_{4}^{-}(a q)\rightleftharpoons2 \mathrm{HCHO}(a q)+\mathrm{H}_{2} \mathrm{O}(l)+\mathrm{IO}_{3}^{-}(a q)\)
\(\text{PO}_4^{3-}\)	\(\left(\mathrm{CH}_{3} \mathrm{O}\right)_{3} \mathrm{PO}(a q)+3 \mathrm{H}_{2} \mathrm{O}(l)\rightleftharpoons3 \mathrm{CH}_{3} \mathrm{OH}(a q)+\mathrm{H}_{3} \mathrm{PO}_{4}(a q)\)
\(\text{C}_2\text{O}_4^{2-}\)	\(\left(\mathrm{C}_{2} \mathrm{H}_{5}\right)_{2} \mathrm{C}_{2} \mathrm{O}_{4}(a q)+2 \mathrm{H}_{2} \mathrm{O}( l)\rightleftharpoons2 \mathrm{C}_{2} \mathrm{H}_{5} \mathrm{OH}(a q)+\mathrm{H}_{2} \mathrm{C}_{2} \mathrm{O}_{4}(a q)\)
\(\text{CO}_3^{2-}\)	\(\mathrm{Cl}_{3} \mathrm{CCOOH}(a q)+2 \mathrm{OH}^{-}(a q)\rightleftharpoons\mathrm{CHCl}_{3}(a q)+\mathrm{CO}_{3}^{2-}(a q)+\mathrm{H}_{2} \mathrm{O}(l)\)

Tabla 8.2.3 . Métodos Gravimétricos de Precipitaciones Seleccionados para Iones Inorgánicos Usando un Precipitante

analito	precipitante	estructura	precipirata formado	precipitado pesado
Ni ^2 ^+	dimetilglioxima		Ni (C 4 H 7 O 2 N 2) 2	Ni (C 4 H 7 O 2 N 2) 2
Fe ^3 ^+	cupferron		Fe (C 6 H 5 N 2 O 2) 3	Fe 2 O 3
Cu ^2 ^+	cupron		CuC 14 H 11 O 2 N	CuC 14 H 11 O 2 N
Co ^2 ^+	1-nitrso-2-naftol		Co (C 10 H 6 O 2 N) 3	Co o CoSO 4
K ^+	tetrafenilborato de sodio	Na [B (C 6 H 5) 4]	K [B (C 6 H 5) 4]	K [B (C 6 H 5) 4]
\(\text{NO}_3^-\)	nitron		C 20 H 16 N 4 HNO 3	C 20 H 16 N 4 HNO 3

La gravimetría de precipitación continúa catalogándose como método estándar para la determinación de\(\text{SO}_4^{2-}\) en el análisis de agua y aguas residuales [Método 4500-SO42— C y Método 4500-SO42— D tal como se publicó en Métodos estándar para el examen de aguas y aguas residuales, 20th Ed., American Public Health Asociación: Wash- ington, D. C., 1998]. La precipitación se lleva a cabo usando BaCl ₂ en una solución ácida (ajustada con HCl a un pH de 4.5—5.0) para evitar la precipitación de BacO ₃ o Ba ₃ (PO ₄) ₂, y a una temperatura cercana al punto de ebullición de la solución. El precipitado se digiere a 80—90 ^o C durante al menos dos horas. Se agrega pulpa de papel de filtro sin cenizas al precipitado para ayudar en su filtración. Después de filtrar, el precipitado se enciende a peso constante a 800 ^o C. Alternativamente, el precipitado se filtra a través de un crisol de vidrio fritado de porosidad fina (sin agregar pulpa de papel de filtro), y se seca a peso constante a 105 ^o C. Este procedimiento se somete a una variedad de errores, incluyendo oclusiones de Ba (NO ₃) ₂, BaCl ₂ y sulfatos alcalinos.

Otros métodos estándar para la determinación del sulfato en agua y aguas residuales incluyen la cromatografía iónica (ver Capítulo 12), la electroforesis iónica capilar (ver Capítulo 12), la turbidimetría (ver Capítulo 10) y el análisis de inyección de flujo (ver Capítulo 13).

Análisis Orgánico

Se pueden determinar varios grupos funcionales orgánicos o heteroátomos mediante métodos gravimétricos de precipitación. Table 8.2.4 proporciona un resumen de varios ejemplos representativos. Nótese que la determinación de grupos funcionales alcoxi es un análisis indirecto en el que el grupo funcional reacciona con y exceso de HI y el I sin reaccionar ^{—determinado} precipitando como AgCl.

Tabla 8.2.4 . Métodos Gravimétricos de Precipitación Seleccionados para Análisis de Grupos Funcionales Orgánicos y Heteroátomos

analito	tratamiento	precipitante	precipitar
halogenuros orgánicos (R- X) donde X es Cl, Br o I	oxidación con HNO 3 en presencia de Ag ^+	AgnO 3	Ag X
halogenuros orgánicos (R-X) donde X es Cl, Br o I	combustión en O 2 (con un catalizador de Pt) en presencia de Ag+	AgnO 3	AgX
azufre orgánico	oxidación con HNO 3 en presencia de Ba ^2+	BacL 2	BasO 4
azufre orgánico	combustión en O 2 (con catalizador de Pt) con SO 2 y SO 3 recogidos en H 2 O 2 diluido	BacL 2	BasO 4
grupos alcoxi (-O-R o -COO-R) donde R es —CH 3 o —C 2H 5	reacción con HI para producir RI	AgnO 3	AGi

Cálculos cuantitativos

La estequiometría de una reacción de precipitación proporciona una relación matemática entre el analito y el precipitado. Debido a que un método gravimétrico de precipitación puede implicar reacciones químicas adicionales para llevar el analito a una forma química diferente, conocer la estequiometría de la reacción de precipitación no siempre es suficiente. Incluso si no tienes un conjunto completo de reacciones químicas balanceadas, puedes usar una conservación de masa para deducir la relación matemática entre el analito y el precipitado. El siguiente ejemplo demuestra este enfoque para el análisis directo de un solo analito.

Ejemplo 8.2.1

Para determinar la cantidad de magnetita, Fe ₃ O ₄, en un mineral impuro, se disuelve una muestra de 1.5419-g en HCl concentrado, resultando en una mezcla de Fe ^{2 +} y Fe ^{3 +}. Después de agregar HNO ₃ para oxidar Fe ²⁺ a Fe ^{3 +} y diluir con agua, el Fe ^{3 +} se precipita como Fe (OH) ₃ usando NH ₃. Filtrar, enjuagar e inflamar el precipitado proporciona 0.8525 g de Fe ₂ O ₃ puro. Calcular el% w/w Fe ₃ O ₄ en la muestra.

Solución

Una conservación de la masa requiere que el precipitado de Fe ₂ O ₃ contenga todo el hierro originalmente en la muestra de mineral. Sabemos que hay 2 moles de Fe por mol de Fe ₂ O ₃ (FW = 159.69 g/mol) y 3 moles de Fe por mol de Fe ₃ O ₄ (FW = 231.54 g/mol); así

\[0.8525 \ \mathrm{g} \ \mathrm{Fe}_{2} \mathrm{O}_{3} \times \frac{2 \ \mathrm{mol} \ \mathrm{Fe}}{159.69 \ \mathrm{g} \ \mathrm{Fe}_{2} \mathrm{O}_{3}} \times \frac{231.54 \ \mathrm{g} \ \mathrm{Fe}_{3} \mathrm{O}_{4}}{3 \ \mathrm{mol} \ \mathrm{Fe}}=0.82405 \ \mathrm{g} \ \mathrm{Fe}_{3} \mathrm{O}_{4} \nonumber\]

El% p/p Fe ₃ O ₄ en la muestra, por lo tanto, es

\[\frac{0.82405 \ \mathrm{g} \ \mathrm{Fe}_{3} \mathrm{O}_{4}}{1.5419 \ \mathrm{g} \ \text { sample }} \times 100=53.44 \% \nonumber\]

Ejercicio 8.2.2

Una muestra de 0.7336-g de una aleación que contiene cobre y zinc se disuelve en HCl 8 M y se diluye a 100 mL en un matraz aforado. En un análisis, el zinc en una porción de 25.00 mL de la solución se precipita como ZnNH ₄ PO ₄, y se aísla como Zn _{2 P 2} O ₇, produciendo 0.1163 g. El cobre en una porción separada de 25.00 mL de la solución se trata para precipitar CuSCn, produciendo 0.2383 g. Calcular el% w/w de Zn y el %w/w de Cu en la muestra.

Contestar

Una conservación de la masa requiere que todo el zinc de la aleación se encuentre en el producto final, Zn ₂ P ₂ O ₇. Sabemos que hay 2 moles de Zn por mol de Zn ₂ P ₂ O ₇; así

\[0.1163 \ \mathrm{g} \ \mathrm{Zn}_{2} \mathrm{P}_{2} \mathrm{O}_{7} \times \frac{2 \ \mathrm{mol} \ \mathrm{Zn}}{304.70 \ \mathrm{g}\ \mathrm{Zn}_{2} \mathrm{P}_{2} \mathrm{O}_{7}} \times \frac{65.38 \ \mathrm{g} \ \mathrm{Zn}}{\mathrm{mol} \ \mathrm{Zn}}=0.04991 \ \mathrm{g} \ \mathrm{Zn}\nonumber\]

Esta es la masa de Zn en 25% de la muestra (una porción de 25.00 mL del volumen total de 100.0 mL). El% p/p de Zn, por lo tanto, es

\[\frac{0.04991 \ \mathrm{g} \ \mathrm{Zn} \times 4}{0.7336 \ \mathrm{g} \text { sample }} \times 100=27.21 \% \ \mathrm{w} / \mathrm{w} \mathrm{Zn} \nonumber\]

Para el cobre, encontramos que

\[\begin{array}{c}{0.2383 \ \mathrm{g} \ \mathrm{CuSCN} \times \frac{1 \ \mathrm{mol} \ \mathrm{Zn}}{121.63 \ \mathrm{g} \ \mathrm{CuSCN}} \times \frac{63.55 \ \mathrm{g} \ \mathrm{Cu}}{\mathrm{mol} \ \mathrm{Cu}}=0.1245 \ \mathrm{g} \ \mathrm{Cu}} \\ {\frac{0.1245 \ \mathrm{g} \ \mathrm{Cu} \times 4}{0.7336 \ \mathrm{g} \text { sample }} \times 100=67.88 \% \ \mathrm{w} / \mathrm{w} \mathrm{Cu}}\end{array} \nonumber\]

En el Ejercicio Práctico 8.2.2 la muestra contiene dos analitos. Debido a que podemos precipitar cada analito selectivamente, encontrar sus respectivas concentraciones es un cálculo estequiométrico sencillo. Pero, ¿y si no podemos precipitar por separado los dos analitos? Para encontrar las concentraciones de ambos analitos, aún necesitamos generar dos precipitados, al menos uno de los cuales debe contener ambos analitos. Aunque esto complica los cálculos, todavía podemos usar una conservación de masa para resolver el problema.

Ejemplo 8.2.2

Una muestra de 0.611-g de una aleación que contiene Al y Mg se disuelve y trata para evitar interferencias por los otros constituyentes de la aleación. El aluminio y el magnesio se precipitan usando 8-hidroxiquinolina, lo que produce un precipitado mixto de Al (C ₉ H ₆ NO) ₃ y Mg (C ₉ H ₆ NO) ₂ que pesa 7.815 g. Encendiendo el precipitado lo convierte en una mezcla de Al ₂ O ₃ y MgO que pesa 1.002 g. Calcular el% w/w Al y el% w/w Mg en la aleación.

Solución

Las masas de los sólidos nos proporcionan las siguientes dos ecuaciones.

\[\mathrm{g} \ \mathrm{Al}\left(\mathrm{C}_{9} \mathrm{H}_{6} \mathrm{NO}\right)_{3}+ \ \mathrm{g} \ \mathrm{Mg}\left(\mathrm{C}_{9} \mathrm{H}_{6} \mathrm{NO}\right)_{2}=7.815 \ \mathrm{g} \nonumber\]

\[\mathrm{g} \ \mathrm{Al}_{2} \mathrm{O}_{3}+\mathrm{g} \ \mathrm{MgO}=1.002 \ \mathrm{g} \nonumber\]

Con dos ecuaciones y cuatro incógnitas, necesitamos dos ecuaciones adicionales para resolver el problema. Una conservación de la masa requiere que todo el aluminio en Al (C ₉ H ₆ NO) ₃ también esté en Al ₂ O ₃; así

\[\mathrm{g} \ \mathrm{Al}_{2} \mathrm{O}_{3}=\mathrm{g} \ \mathrm{Al}\left(\mathrm{C}_{9} \mathrm{H}_{6} \mathrm{NO}\right)_{3} \times \frac{1 \ \mathrm{mol} \ \mathrm{Al}}{459.43 \ \mathrm{g} \ \mathrm{Al}\left(\mathrm{C}_{9} \mathrm{H}_{6} \mathrm{NO}\right)_{3}} \times \frac{101.96 \ \mathrm{g} \ \mathrm{Al}_{2} \mathrm{O}_{3}}{2 \ \mathrm{mol} \ \mathrm{Al}_{2} \mathrm{O}_{3}} \nonumber\]

\[\mathrm{g} \ \mathrm{Al}_{2} \mathrm{O}_{3}=0.11096 \times \mathrm{g} \ \mathrm{Al}\left(\mathrm{C}_{9} \mathrm{H}_{6} \mathrm{NO}\right)_{3} \nonumber\]

Usando el mismo enfoque, una conservación de la masa para el magnesio da

\[\mathrm{g} \ \mathrm{MgO}=\mathrm{g} \ \mathrm{Mg}\left(\mathrm{C}_{9} \mathrm{H}_{6} \mathrm{NO}\right)_{2} \times \frac{1 \ \mathrm{mol} \ \mathrm{Mg}}{312.61 \ \mathrm{g} \ \mathrm{Mg}\left(\mathrm{C}_{9} \mathrm{H}_{6} \mathrm{NO}\right)_{2}} \times \frac{40.304 \ \mathrm{g} \ \mathrm{MgO}}{\mathrm{mol} \ \mathrm{MgO}} \nonumber\]

\[\mathrm{g} \ \mathrm{MgO}=0.12893 \times \mathrm{g} \ \mathrm{Mg}\left(\mathrm{C}_{9} \mathrm{H}_{6} \mathrm{NO}\right)_{2} \nonumber\]

Sustituir las ecuaciones por g MgO y g Al ₂ O ₃ en la ecuación para los pesos combinados de MgO y Al ₂ O ₃ nos deja con dos ecuaciones y dos incógnitas.

\[\mathrm{g} \ \mathrm{Al}\left(\mathrm{C}_{9} \mathrm{H}_{6} \mathrm{NO}\right)_{3}+\mathrm{g} \ \mathrm{Mg}\left(\mathrm{C}_{9} \mathrm{H}_{6} \mathrm{NO}\right)_{2}=7.815 \ \mathrm{g} \nonumber\]

\[0.11096 \times \mathrm{g} \ \mathrm{Al}\left(\mathrm{C}_{9} \mathrm{H}_{6} \mathrm{NO}\right)_{3}+ 0.12893 \times \mathrm{g} \ \mathrm{Mg}\left(\mathrm{C}_{9} \mathrm{H}_{6} \mathrm{NO}\right)_{2}=1.002 \ \mathrm{g} \nonumber\]

Multiplicar la primera ecuación por 0.11096 y restar la segunda ecuación da

\[-0.01797 \times \mathrm{g} \ \mathrm{Mg}\left(\mathrm{C}_{9} \mathrm{H}_{6} \mathrm{NO}\right)_{2}=-0.1348 \ \mathrm{g} \nonumber\]

\[\mathrm{g} \ \mathrm{Mg}\left(\mathrm{C}_{9} \mathrm{H}_{6} \mathrm{NO}\right)_{2}=7.504 \ \mathrm{g} \nonumber\]

\[\mathrm{g} \ \mathrm{Al}\left(\mathrm{C}_{9} \mathrm{H}_{6} \mathrm{NO}\right)_{3}=7.815 \ \mathrm{g}-7.504 \ \mathrm{g} \ \mathrm{Mg}\left(\mathrm{C}, \mathrm{H}_{6} \mathrm{NO}\right)_{2}=0.311 \ \mathrm{g} \nonumber\]

Ahora podemos terminar el problema usando el enfoque de Example 8.2.1 . Una conservación de la masa requiere que todo el aluminio y magnesio en la muestra original de metal Dow esté en los precipitados de Al (C ₉ H ₆ NO) ₃ y el Mg (C ₉ H ₆ NO) ₂. Para el aluminio, encontramos que

\[0.311 \ \mathrm{g} \ \mathrm{Al}\left(\mathrm{C}_{9} \mathrm{H}_{6} \mathrm{NO}\right)_{3} \times \frac{1 \ \mathrm{mol} \ \mathrm{Al}}{459.45 \ \mathrm{g} \ \mathrm{Al}\left(\mathrm{C}_{9} \mathrm{H}_{6} \mathrm{NO}\right)_{3}} \times \frac{26.982 \ \mathrm{g} \ \mathrm{Al}}{\mathrm{mol} \ \mathrm{Al}}=0.01826 \ \mathrm{g} \ \mathrm{Al} \nonumber\]

\[\frac{0.01826 \ \mathrm{g} \ \mathrm{Al}}{0.611 \ \mathrm{g} \text { sample }} \times 100=2.99 \% \mathrm{w} / \mathrm{w} \mathrm{Al} \nonumber\]

y para el magnesio tenemos

\[7.504 \ \text{g Mg}\left(\mathrm{C}_9 \mathrm{H}_{6} \mathrm{NO}\right)_{2} \times \frac{1 \ \mathrm{mol} \ \mathrm{Mg}}{312.61 \ \mathrm{g} \ \mathrm{Mg}\left(\mathrm{C}_9 \mathrm{H}_{6} \mathrm{NO}\right)_{2}} \times \frac{24.305 \ \mathrm{g} \ \mathrm{Mg}}{\mathrm{mol} \ \mathrm{MgO}}=0.5834 \ \mathrm{g} \ \mathrm{Mg} \nonumber\]

\[\frac{0.5834 \ \mathrm{g} \ \mathrm{Mg}}{0.611 \ \mathrm{g} \text { sample }} \times 100=95.5 \% \mathrm{w} / \mathrm{w} \mathrm{Mg} \nonumber\]

Ejercicio 8.2.3

Una muestra de roca de silicato que pesa 0.8143 g se pone en solución y se trata para producir una mezcla de 0.2692-g de NaCl y KCl. La mezcla de sales de cloruro se disuelve en una mezcla de etanol y agua, y se trata con HClO ₄, precipitando 0.3314 g de KClO ₄. ¿Cuál es el% w/w de Na ₂ O en la roca de silicato?

Contestar

Las masas de los sólidos nos proporcionan las siguientes ecuaciones

\[\mathrm{g} \ \mathrm{NaCl}+\mathrm{g} \ \mathrm{KCl}=0.2692 \ \mathrm{g} \nonumber\]

\[\mathrm{g} \ \mathrm{KClO}_{4} = 0.3314 \ \mathrm{g} \nonumber\]

Con dos ecuaciones son tres desconocidas —g NaCl, g KCl y g KClO ₄ — necesitamos una ecuación adicional para resolver el problema. Una conservación de la masa requiere que todo el potasio originalmente en el KCl termine en el KClO ₄; así

\[\text{g KClO}_4 = \text{g KCl} \times \frac{1 \text{ mol Cl}}{74.55 \text{ g KCl}} \times \frac {138.55 \text{ g KClO}_4}{\text{mol Cl}} = 1.8585 \times \text{ g KCl} \nonumber\]

Dada la masa de KClO ₄, utilizamos la tercera ecuación para resolver la masa de KCl en la mezcla de sales de cloruro

\[\text{ g KCl} = \frac{\text{g KClO}_4}{1.8585} = \frac{0.3314 \text{ g}}{1.8585} = 0.1783 \text{ g KCl} \nonumber\]

La masa de NaCl en la mezcla de sales de cloruro, por lo tanto, es

\[\text{ g NaCl} = 0.2692 \text{ g} - \text{g KCl} = 0.2692 \text{ g} - 0.1783 \text{ g KCl} = 0.0909 \text{ g NaCl} \nonumber\]

Finalmente, para reportar el% w/w de Na ₂ O en la muestra, se utiliza una conservación de masa sobre sodio para determinar la masa de Na ₂ O

\[0.0909 \text{ g NaCl} \times \frac{1 \text{ mol Na}}{58.44 \text{ g NaCl}} \times \frac{61.98 \text{ g Na}_2\text{O}}{2 \text{ mol Na}} = 0.0482 \text{ g Na}_2\text{O} \nonumber\]

dando el% p/p de Na ₂ O como

\[\frac{0.0482 \text{ g Na}_2\text{O}}{0.8143 \text{ g sample}} \times 100 = 5.92\% \text{ w/w Na}_2\text{O} \nonumber\]

Los problemas anteriores son ejemplos de métodos directos de análisis debido a que el precipitado contiene el analito. En un análisis indirecto el precipitado se forma como resultado de una reacción con el analito, pero el analito no forma parte del precipitado. Como muestra el siguiente ejemplo, a pesar de la complejidad adicional, todavía podemos usar principios de conservación para organizar nuestros cálculos.

Ejemplo 8.2.3

Una muestra impura de Na ₃ PO ₃ que pesa 0.1392 g se disuelve en 25 mL de agua. Se prepara una segunda solución que contiene 50 mL de HgCl ₂ al 3% p/v, 20 mL de acetato de sodio al 10% p/v y 5 mL de ácido acético glacial. Agregar la solución que contiene la muestra a la segunda solución se oxida\(\text{PO}_3^{3-}\)\(\text{PO}_4^{3-}\) y precipita Hg ₂ Cl ₂. Después de digerir, filtrar y enjuagar el precipitado, se obtienen 0.4320 g de Hg _{2 Cl 2}. Reportar la pureza de la muestra original como% w/w Na ₃ PO ₃.

Solución

Este es un ejemplo de un análisis indirecto porque el precipitado, Hg ₂ Cl ₂, no contiene el analito, Na ₃ PO ₃. Aunque la estequiometría de la reacción entre Na ₃ PO ₃ y HgCl ₂ se da anteriormente en el capítulo, veamos cómo podemos resolver el problema usando principios de conservación. (Aunque puedes escribir las reacciones equilibradas para cualquier análisis, ¡aplicar principios de conservación te puede ahorrar una cantidad significativa de tiempo! )

La reacción entre Na ₃ PO ₃ y HgCl ₂ es una reacción de oxidación-reducción en la que el fósforo aumenta su estado de oxidación de +3 en Na ₃ PO ₃ a +5 en Na ₃ PO _4, y en la que el mercurio disminuye su estado de oxidación de +2 en HgCl ₂ a +1 en Hg ₂ Cl ₂. Una reacción redox debe obedecer a una conservación de electrones porque todos los electrones liberados por el agente reductor, Na ₃ PO ₃, deben ser aceptados por el agente oxidante, HgCl ₂. Sabiendo esto, escribimos los siguientes factores de conversión estequiométricos:

\[\frac{2 \ \mathrm{mol} \ e^{-}}{\mathrm{mol} \ \mathrm{Na}_{3} \mathrm{PO}_{3}} \text { and } \frac{1 \mathrm{mol} \ e^{-}}{\mathrm{mol} \ \mathrm{HgCl}_{2}} \nonumber\]

Ahora estamos listos para resolver el problema. Primero, utilizamos una conservación de masa para mercurio para convertir la masa del precipitado a los moles de HgCl ₂.

\[0.4320 \ \mathrm{g} \ \mathrm{Hg}_{2} \mathrm{Cl}_{2} \times \frac{2 \ \mathrm{mol} \ \mathrm{Hg}}{472.09 \ \mathrm{g} \ \mathrm{Hg}_{2} \mathrm{Cl}_{2}} \times \frac{1 \ \mathrm{mol} \ \mathrm{HgCl}_{2}}{\mathrm{mol} \ \mathrm{Hg}}=1.8302 \times 10^{-3} \ \mathrm{mol} \ \mathrm{HgCl}_{2} \nonumber\]

A continuación, utilizamos la conservación de electrones para encontrar la masa de Na ₃ PO ₃.

\[1.8302 \times 10^{-3} \ \mathrm{mol} \ \mathrm{HgCl}_{2} \times \frac{1 \ \mathrm{mol} \ e^{-}}{\mathrm{mol} \ \mathrm{HgCl}_{2}} \times \frac{1 \ \mathrm{mol} \ \mathrm{Na}_{3} \mathrm{PO}_{4}}{2 \ \mathrm{mol} \ e^{-}} \times \frac{147.94 \ \mathrm{g} \ \mathrm{Na}_{3} \mathrm{PO}_{3}}{\mathrm{mol} \ \mathrm{Na}_{3} \mathrm{PO}_{3}}=0.13538 \ \mathrm{g} \ \mathrm{Na}_{3} \mathrm{PO}_{3} \nonumber\]

Finalmente, calculamos el% w/w Na ₃ PO ₃ en la muestra.

\[\frac{0.13538 \ \mathrm{g} \ \mathrm{Na}_{3} \mathrm{PO}_{3}}{0.1392 \ \mathrm{g} \text { sample }} \times 100=97.26 \% \mathrm{w} / \mathrm{w} \mathrm{Na}_{3} \mathrm{PO}_{3} \nonumber\]

A medida que se sienta cómodo usando los principios de conservación, verá formas de simplificar aún más los problemas. Por ejemplo, una conservación de electrones requiere que los electrones liberados por Na _{3 PO 3} terminen en el producto, Hg _{2 Cl 2}, produciendo el siguiente factor de conversión estequiométrico:

\[\frac{2 \ \operatorname{mol} \ \mathrm{Na}_{3} \mathrm{PO}_{3}}{\mathrm{mol} \ \mathrm{Hg}_{2} \mathrm{Cl}_{2}} \nonumber\]

Este factor de conversión proporciona un vínculo directo entre la masa de Hg ₂ Cl ₂ y la masa de Na ₃ PO ₃.

Ejercicio 8.2.4

Un enfoque para determinar el fosfato\(\text{PO}_4^{3-}\),, es precipitarlo como fosfomolibdato amónico, (NH ₄) ₃ PO ₄ •12MoO ₃. Después de aislar el precipitado por filtración, lo disolvemos en ácido y precipitamos y pesamos el molibdato como PbMoO ₃. Supongamos que sabemos que nuestra muestra es al menos 12.5% Na ₃ PO ₄ y que necesitamos recuperar un mínimo de 0.600 g de PbMoO ₃? ¿Cuál es la cantidad mínima de muestra que necesitamos para cada análisis?

Contestar

Para encontrar la masa de (NH ₄) ₃ PO ₄ •12MoO ₃ que producirá 0.600 g de PbMoO ₃, primero usamos una conservación de masa para molibdeno; así

\[0.600 \ \mathrm{g} \ \mathrm{PbMoO}_{3} \times \frac{1 \ \mathrm{mol} \ \mathrm{Mo}}{351.2 \ \mathrm{g} \ \mathrm{PbMoO}_{3}} \times \frac{1876.59 \ \mathrm{g} \ \left(\mathrm{NH}_{4}\right)_{3} \mathrm{PO}_{4} \cdot 12 \mathrm{MoO}_{3}}{12 \ \mathrm{mol} \ \mathrm{Mo}}= 0.2672 \ \mathrm{g} \ \left(\mathrm{NH}_{4}\right)_{3} \mathrm{PO}_{4} \cdot 12 \mathrm{MoO}_{3} \nonumber\]

A continuación, para convertir esta masa de (NH ₄) ₃ PO ₄ •12MoO ₃ a una masa de Na ₃ PO ₄, utilizamos una conservación de masa en\(\text{PO}_4^{3-}\).

\[0.2672 \ \mathrm{g} \ \left(\mathrm{NH}_{4}\right)_{3} \mathrm{PO}_{4} \cdot 12 \mathrm{MoO}_{3} \times \frac{1 \ \mathrm{mol} \ \mathrm{PO}_{4}^{3-}}{1876.59 \ \mathrm{g \ }\left(\mathrm{NH}_{4}\right)_{3} \mathrm{PO}_{4} \cdot 12 \mathrm{MoO}_{3}} \times \frac{163.94 \ \mathrm{g} \ \mathrm{Na}_{3} \mathrm{PO}_{4}}{\mathrm{mol} \ \mathrm{PO}_{4}^{3-}}=0.02334 \ \mathrm{g} \ \mathrm{Na}_{3} \mathrm{PO}_{4} \nonumber\]

Finalmente, convertimos esta masa de Na ₃ PO ₄ a la masa de muestra correspondiente.

\[0.02334 \ \mathrm{g} \ \mathrm{Na}_{3} \mathrm{PO}_{4} \times \frac{100 \ \mathrm{g} \text { sample }}{12.5 \ \mathrm{g} \ \mathrm{Na}_{3} \mathrm{PO}_{4}}=0.187 \ \mathrm{g} \text { sample } \nonumber\]

Una muestra de 0.187 g es suficiente para garantizar que recuperamos un mínimo de 0.600 g de PbMoO ₃. Si una muestra contiene más de 12.5% Na ₃ PO ₄, entonces una muestra de 0.187 g producirá más de 0.600 g de PbMoO ₃.

Aplicaciones Cualitativas

Una reacción de precipitación es un método útil para identificar analitos inorgánicos y orgánicos. Debido a que un análisis cualitativo no requiere mediciones cuantitativas, la señal analítica es simplemente la observación de que se forma un precipitado. Aunque las aplicaciones cualitativas de la gravimetría de precipitación han sido reemplazadas por métodos espectroscópicos de análisis, continúan encontrando aplicación en pruebas puntuales para la presencia de analitos específicos [Jungreis, E. Spot Test Analysis; 2nd Ed., Wiley: New York, 1997].

Cualquiera de los precipitantes enumerados en Table 8.2.1 , Table 8.2.3 y Table 8.2.4 se puede utilizar para un análisis cualitativo.

Evaluando Gravimetría de Precipitación

Escala de Operación

La escala de operación para gravimetría de precipitación está limitada por la sensibilidad del balance y la disponibilidad de muestra. Para lograr una precisión de ± 0.1% utilizando una balanza analítica con una sensibilidad de ±0.1 mg, debemos aislar al menos 100 mg de precipitado. Como consecuencia, la gravimetría de precipitación generalmente se limita a analitos mayores o menores, en muestras macro o meso. El análisis de un analito a nivel de traza o una micromuestra requiere un balance microanalítico.

Precisión

Para una macro muestra que contiene un analito mayor, se logra rutinariamente un error relativo de 0.1— 0.2%. Las principales limitaciones son las pérdidas de solubilidad, las impurezas en el precipitado y la pérdida de precipitado durante el manejo. Cuando es difícil obtener un precipitado que esté libre de impurezas, a menudo es posible determinar una relación empírica entre la masa del precipitado y la masa del analito mediante una calibración apropiada.

Precisión

La precisión relativa de la gravimetría de precipitación depende del tamaño de la muestra y de la masa del precipitado. Para una menor cantidad de muestra o precipitado, se obtiene rutinariamente una precisión relativa de 1—2 ppt. Cuando se trabaja con mayores cantidades de muestra o precipitado, la precisión relativa se extiende a varias ppm. Pocas técnicas cuantitativas pueden lograr este nivel de precisión.

Sensibilidad

Para cualquier método gravimétrico de precipitación podemos escribir la siguiente ecuación general para relacionar la señal (gramos de precipitado) con la cantidad absoluta de analito en la muestra

\[\text { g precipitate }=k \times \mathrm{g} \text { analyte } \label{8.13}\]

donde k, la sensibilidad del método, está determinada por la estequiometría entre el precipitado y el analito.

La ecuación\ ref {8.13} asume que usamos un blanco adecuado para corregir la señal para cualquier contribución del reactivo a la masa del precipitado.

Consideremos, por ejemplo, la determinación de Fe como Fe ₂ O ₃. Usando una conservación de la masa para el hierro, la masa del precipitado es

\[\mathrm{g} \ \mathrm{Fe}_{2} \mathrm{O}_{3}=\mathrm{g} \ \mathrm{Fe} \times \frac{1 \ \mathrm{mol} \ \mathrm{Fe}}{\text{AW Fe}} \times \frac{\text{FW Fe}_{2} \mathrm{O}_{3}}{2 \ \mathrm{mol} \ \mathrm{Fe}} \nonumber\]

y el valor de k es

\[k=\frac{1}{2} \times \frac{\mathrm{FW} \ \mathrm{Fe}_{2} \mathrm{O}_{3}}{\mathrm{AW} \ \mathrm{Fe}} \label{8.14}\]

Como podemos ver en la Ecuación\ ref {8.14}, hay dos formas de mejorar la sensibilidad de un método. La forma más obvia de mejorar la sensibilidad es aumentar la relación entre la masa molar del precipitado y la del analito. En otras palabras, ayuda a formar un precipitado con el mayor peso de fórmula posible. Una forma menos obvia de mejorar la sensibilidad de un método se indica con el término 1/2 en la Ecuación\ ref {8.14}, que da cuenta de la estequiometría entre el analito y el precipitado. También podemos mejorar la sensibilidad formando un precipitado que contenga menos unidades del analito.

Ejercicio 8.2.5

Supongamos que desea determinar la cantidad de hierro en una muestra. ¿Cuál de los siguientes compuestos —Feo, Fe ₂ O ₃, o Fe ₃ O ₄ — proporciona la mayor sensibilidad?

Contestar

Para determinar qué forma tiene la mayor sensibilidad, utilizamos una conservación de masa para el hierro para encontrar la relación entre la masa del precipitado y la masa de hierro.

\[\begin{aligned} \mathrm{g} \ \mathrm{FeO} &=\mathrm{g} \ \mathrm{Fe} \times \frac{1 \ \mathrm{mol} \ \mathrm{Fe}}{55.85 \ \mathrm{g} \ \mathrm{Fe}} \times \frac{71.84 \ \mathrm{g} \ \mathrm{FeO}}{\mathrm{mol} \ \mathrm{Fe}}=1.286 \times \mathrm{g} \ \mathrm{Fe} \\ \mathrm{g} \ \mathrm{Fe}_{2} \mathrm{O}_{3} &=\mathrm{g} \ \mathrm{Fe} \times \frac{1 \ \mathrm{mol} \ \mathrm{Fe}}{55.85 \ \mathrm{g} \ \mathrm{Fe}} \times \frac{159.69 \ \mathrm{g} \ \mathrm{Fe}_{2} \mathrm{O}_{3}}{2 \ \mathrm{mol} \ \mathrm{Fe}}=1.430 \times \mathrm{g} \ \mathrm{Fe} \\ \mathrm{g} \ \mathrm{Fe}_{3} \mathrm{O}_{4} &=\mathrm{g} \ \mathrm{Fe} \times \frac{1 \ \mathrm{mol} \ \mathrm{Fe}}{55.85 \ \mathrm{g} \ \mathrm{Fe}} \times \frac{231.53 \ \mathrm{g} \ \mathrm{Fe}_{3} \mathrm{O}_{4}}{3 \ \mathrm{mol} \ \mathrm{Fe}}=1.382 \times \mathrm{g} \ \mathrm{Fe} \end{aligned} \nonumber\]

De las tres opciones, la mayor sensibilidad se obtiene con Fe ₂ O ₃ porque proporciona el mayor valor para k.

Selectividad

Debido a la naturaleza química del proceso de precipitación, los precipitantes generalmente no son selectivos para un solo analito. Por ejemplo, la plata no es un precipitante selectivo para el cloruro porque también forma precipitados con bromuro y con yoduro. Los interferentes suelen ser un problema grave y deben considerarse para obtener resultados precisos.

Tiempo, Costo y Equipo

La gravimetría de precipitación requiere mucho tiempo y rara vez es práctica si se tiene una gran cantidad de muestras para analizar; sin embargo, debido a que gran parte del tiempo invertido en gravimetría de precipitación no requiere la supervisión inmediata de un analista, es una alternativa práctica cuando se trabaja con solo unas pocas muestras. Las necesidades de equipo son pocas (vasos de precipitados, dispositivos de filtrado, hornos o quemadores y balanzas) económicas, disponibles de forma rutinaria en la mayoría de los laboratorios y fáciles de mantener.