1.5: Fórmula de punto medio
- Page ID
- 107621
Determinar los puntos medios de los segmentos de línea tomando el promedio de\(x\) valores y el promedio de\(y\) valores
Supongamos que un plano de coordenadas se transpuso sobre un mapa del metro, y la línea azul iba en línea recta del punto\(\left(-9, 8\right)\) al punto\(\left(1, -4\right)\). Si te subiste a la línea azul al inicio de la línea y viajaste a mitad de camino hasta el final de la línea, ¿cuáles serían tus coordenadas? ¿Cómo calcularías estas coordenadas?
Considera la siguiente situación: Vives en Des Moines, Iowa y tus abuelos viven en Houston, Texas. Planeas visitarlos para el verano y tus padres acuerdan reunirse con tus abuelos a mitad de camino para intercambiarte. ¿Cómo encuentras esta ubicación?
Al encontrar algo “a mitad de camino”, estás encontrando el punto medio de la línea recta que conecta los dos segmentos. En la situación anterior, el punto medio estaría a medio camino entre Des Moines y Houston.
El punto medio entre dos pares de coordenadas representa el punto medio, o el promedio. Es el par ordenado\(\left(x_m, y_m\right)\) donde:
\(\left(x_m,y_m\right)=\left(\dfrac{x_1+x_2}{2} , \dfrac{y_1+y_2}{2}\right)\)
Encontremos la ubicación que está a medio camino entre Des Moines y Houston dada la información de arriba:
Des Moines, Iowa tiene las coordenadas\(\left(41.59, 93.62\right)\).
Houston, Texas tiene las coordenadas\(\left(29.76, 95.36\right)\).
Encuentra las coordenadas del punto medio entre estas dos ciudades.
Decidir qué par ordenado representará
\(\left(x_1, y_1\right)\)y que representará\(\left(x_2, y_2\right)\).
\(\left(x_1, y_1\right )=\left(41.59,93.62\right)\)
\(\left(x_2, y_2\right)=\left(29.76,95.36\right)\)
Calcular el punto medio usando la fórmula
\(\left(x_m,y_m\right )=\left(\dfrac{x_1+x_2}{2} , \dfrac{y_1+y_2}{2}\right)\)
\(\left(x_m,y_m\right )=\left(\dfrac{41.59+29.76}{2} , \dfrac{93.62+95.36}{2}\right)\)
\(\left(x_m,y_m\right)=\left (35.675,94.49\right)\)
Usando Google Maps, puedes reunirte en el Bosque Nacional Ozark, a medio camino entre las dos ciudades.
Ahora, completemos los siguientes problemas usando la fórmula de punto medio:
- Un segmento con puntos finales\(\left(9, –2\right)\) y\(\left(x_1, y_1\right)\) tiene un punto medio de\(\left(2, –6\right)\). Encuentra\(\left(x_1, y_1\right)\).
Utilice la fórmula de punto medio:
\(\dfrac{x_1+x_2}{2}=x_m\)
\(2=\dfrac{x_1+9}{2} \rightarrow 4=x_1+9\)
\(x_1 = -5\)
Siguiendo el mismo procedimiento:
\(\dfrac{y_1+(−2)}{2} = −6 \rightarrow y_1+(−2)=−12\)
\(y_1=−10\)
\(\left(x_1,y_1)=(−5,−10\right)\)
- Encuentra los valores de x e y que hacen\(\left(9.5,6\right)\) el punto medio de\(\left(3,5\right)\) y\(\left(x,y\right)\).
Comience con la fórmula, y resuelva para las variables:
La fórmula del punto medio:\(\left(x_m, y_m\right )=\left(\dfrac{x_1+x_2}{2}, \dfrac{y_1+y_2}{2}\right)\)
Sustituir en los valores y variables dados:\(\left(9.5,6\right)=\left(\dfrac{3+x}{2}, \dfrac{5+y}{2}\right)\)
Esto se puede reescribir como dos ecuaciones:
\(9.5=\dfrac{3+x}{2}\);\(6=\dfrac{5+y}{2}\)
Multiplicar cada lado por 2:\(19=3+x\);\(12=5+y\)
Aislar las variables:\(16=x\);\(7=y\)
Ejemplo\(\PageIndex{1}\)
Anteriormente, se le pidió que calculara sus coordenadas después de viajar a mitad de camino hasta el final de la línea azul del metro. Ya sabes que la línea azul va en línea recta de\(\left(-9,8\right)\) al punto\(\left(1, -4\right)\).
Solución
Para calcular estas coordenadas, es necesario calcular el punto medio entre\(\left(-9,8\right)\) y\(\left(1, -4\right)\).
Para encontrar el punto medio entre\(\left(-9,8\right)\) y\(\left(1, -4\right)\), sustituir en los valores dados en la fórmula de punto medio y resolver.
La fórmula del punto medio:\(\left(x_m,y_m\right)=\left(\dfrac{x_1+x_2}{2} , \dfrac{y_1+y_2}{2}\right)\)
Sustituir en los valores y variables dados:\(midpoint=\left(\dfrac{-9+1}{2} , \dfrac{8+(-2)}{2}\right)\)
\(midpoint=\left(−4,2\right)\)
Por lo tanto, las coordenadas del tren subterráneo a mitad de camino por la línea azul son\(\left(-4, 2\right)\).
Ejemplo\(\PageIndex{2}\)
En una caminata, tú y tu amigo deciden tomar diferentes rutas, pero luego se reúnen para almorzar. Caminas 3 millas al norte y 2 millas al oeste. Partiendo del mismo punto, tu amigo camina 4 millas al este y 1 milla al sur. Desde estos puntos, cada uno camina uno hacia el otro, reuniéndose a mitad de camino para almorzar. ¿Dónde estaría su lugar de encuentro a la hora del almuerzo en referencia a su punto de partida?
Solución
Piense en el punto de partida como el origen de un sistema de coordenadas cartesianas. Si caminas hacia el norte 3 millas, eso es caminar recto por la gráfica 3 unidades. Caminar al oeste 2 millas es lo mismo que caminar a la izquierda 2 unidades en la gráfica. Entonces has llegado al punto\(\left(-2, 3\right)\). Para tu amigo, el este está a la derecha (positivo) y el sur está abajo (negativo), por lo que llega a\(\left(4,-1\right)\). Ahora necesitas encontrar el punto medio:
\(\left(x_m,y_m\right)=\left(\dfrac{-2+4}{2} , \dfrac{3+(-12)}{2}\right)=(22,22)=\left(1,1\right)\)
Su lugar de encuentro a la hora del almuerzo sería 1 milla al norte y 1 milla al este de su punto de partida.
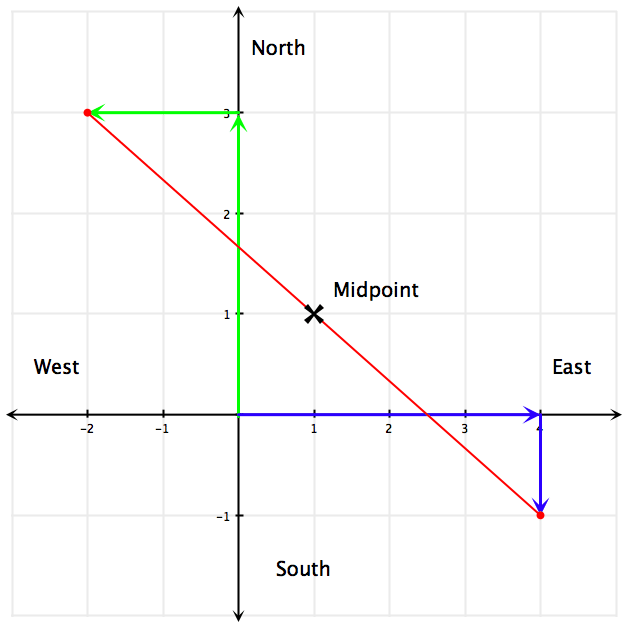Figura\(\PageIndex{1}\)Revisar
En 1—10, encuentra el punto medio del segmento de línea que une los dos puntos.
- \(\left(x_1, y_1\right)\)y\(\left(x_2, y_2\right)\)
- \(\left(7, 7\right)\)y\(\left(–7, 7\right)\)
- \(\left(–3, 6\right)\)y\(\left(3, –6\right)\)
- \(\left(–3, –1\right)\)y\(\left(–5, –8\right)\)
- \(\left(3, –4\right)\)y\(\left(6, 1\right)\)
- \(\left(2, –3\right)\)y\(\left(2, 4\right)\)
- \(\left(4, –5\right)\)y\(\left(8, 2\right)\)
- \(\left(1.8, –3.4\right)\)y\(\left(–0.4, 1.4\right)\)
- \(\left(5, –1\right)\)y\(\left(–4, 0\right)\)
- \(\left(10, 2\right)\)y\(\left(2, –4\right)\)
- Un punto final de un segmento de línea es\(\left(4, 5\right)\) y el punto medio del segmento de línea es\(\left(3, –2\right)\). Encuentra el otro punto final.
- Un punto final de un segmento de línea es\(\left(–10, –2\right)\) y el punto medio del segmento de línea es\(\left(0, 4\right)\). Encuentra el otro punto final.
- Shawn vive seis cuadras al oeste y diez cuadras al norte del centro de la ciudad. Kenia vive catorce cuadras al este y dos cuadras al norte del centro de la ciudad.
- ¿A qué distancia están estas dos chicas “como las moscas del cuervo”?
- ¿Dónde está el punto medio entre sus casas?
Reseña Mixta
- Una población aumenta 1.2% anual. La población actual es de 121,000.
- ¿Cuál será la población en 13 años?
- Suponiendo que esta tasa continúe, ¿cuándo llegará la población a 200 mil?
- Escribir\(1.29651843 \cdot 10^5\) en forma estándar.
- ¿Es\(4, 2, 1,\dfrac{1}{2}, \dfrac{1}{6}, \dfrac{1}{8}, …\) un ejemplo de secuencia geométrica? Explica tu respuesta.
- Simplificar\(6x^3(4xy^{2}+y^{3}z)\).
- Supongamos\(0=(x−2)(x+1)(x−3)\). ¿Cuáles son los\(x\) −intercepts?
- Simplificar\(\sqrt{300}\).
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 11.8.
El vocabulario
| Término | Definición |
|---|---|
| Fórmula de punto medio | La fórmula del punto medio dice que para los puntos finales\(\left(x_1, y_1\right)\) y\(\left(x_2, y_2\right)\), el punto medio es\(\left(\dfrac{x_1+x_2}{2} , \dfrac{y_1+y_2}{2}\right)\). |
| punto medio | El punto medio de dos vectores es la ubicación en el centro de sus puntos finales. |
Recurso Adicional
Elemento Interactivo
Video: Fórmula de punto medio - Descripción general
Actividades: Preguntas de discusión sobre la fórmula de punto medio
Práctica: Fórmula de punto medio
Mundo real: Mapa SF - Pyththm