7.4: Partes correspondientes de figuras similares
- Page ID
- 107434
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Identificar longitudes laterales coincidentes y medidas de ángulo en figuras similares.
María tiene un proyecto de arte debido a la escuela. Ella decide hacer una pequeña réplica de su dormitorio. Comienza midiendo los ángulos de su dormitorio, luego dibuja figuras similares. La figura más grande representa su dormitorio y la figura más pequeña representa su réplica.
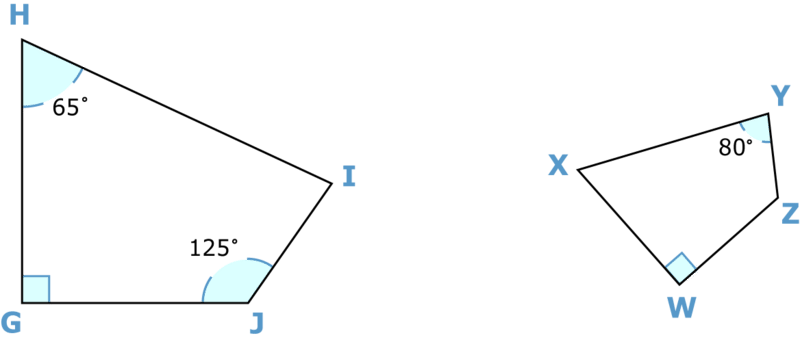
La puerta de su habitación se encuentra en el medio de\(\overline{IJ}\). Para su réplica, la puerta debe colocarse en medio del lado correspondiente. ¿A qué lado de la réplica corresponde\(\overline{IJ}\)?
En este concepto, conocerás los lados correspondientes de figuras similares.
Partes correspondientes de figuras similares
El triángulo ABC es similar al triángulo DEF. Esto quiere decir que si bien tienen la misma forma, no son del mismo tamaño. De hecho, existe una relación entre las partes correspondientes del triángulo.
Las longitudes laterales son correspondientes aunque no sean congruentes. Utilice el símbolo para similar (”\(\sim\) “) para mostrar la relación entre los lados correspondientes de los dos triángulos.
\(\overline{AB}\sim \overline{DE}\)
\(\overline{BC}\sim \overline{EF}\)
\(\overline{AC}\sim \overline{DF}\)
Ejemplo\(\PageIndex{1}\)
Antes, te dieron un problema sobre María y su dormitorio.
Ella está haciendo una réplica de su dormitorio para su clase de arte. Dibuja dos figuras similares para asegurarse de que está colocando todo en la posición correcta.
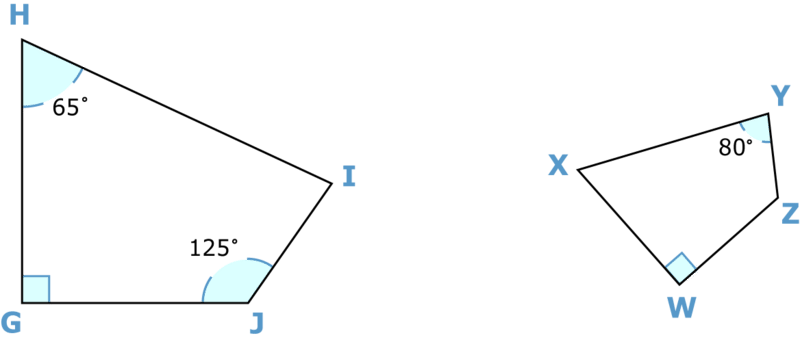
Solución
Ella necesita colocar la puerta de su habitación en el medio del lado que le corresponde\(\overline{IJ}\). ¿A qué lado corresponde\(\overline{IJ}\)?
Primero, gira la segunda figura para que se vea como la primera figura.
Después, ubique el costado en la segunda figura que esté en la posición que\(\overline{IJ}\) está en la primera figura.
\(\overline{YZ}\)
La respuesta es que\(\overline{YZ}\) corresponde a\(\overline{IJ}\). María necesita colocar la puerta de su habitación en el centro de\(\overline{YZ}\) la réplica.
Ejemplo\(\PageIndex{2}\)
Las cifras que aparecen a continuación son similares. ¿De qué lado corresponde\(\overline{NO}\)?
Figura\(\PageIndex{5}\)Solución
Primero, posiciona la segunda figura para que se vea como la primera figura.
Después, identificar el lado en la segunda figura que está en la misma\(\overline{NO}\) posición que en la primera figura.
\(\overline{QR}\)
La respuesta es que\(\overline{QR}\) corresponde a\(\overline{NO}\).
Ejemplo\(\PageIndex{3}\)
\(\overline{AB}\sim _____\)
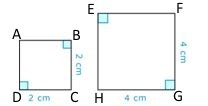
Solución
Primero, mira para ver qué lado del segundo triángulo corresponde al segmento dado.
\(\overline{EF}\)
Entonces, completa el problema.
\(\overline{AB}\sim \overline{EF}\)
La respuesta es esa\(\overline{AB}\sim \overline{EF}\).
Ejemplo\(\PageIndex{4}\)
¿Qué hace que los dos cuadrados sean similares si ambos tienen cuatro ángulos rectos?
Solución
Primero, comprueba si las longitudes laterales son las mismas.
No
A continuación, revisa para ver si la forma es la misma.
Sí
Entonces, exponer por qué los dos cuadrados son similares.
Misma forma, diferentes tamaños
La respuesta es que los dos cuadrados son similares porque tienen la misma forma, pero diferentes tamaños.
Ejemplo\(\PageIndex{5}\)
En el par de triángulos, ¿los dos triángulos son similares o congruentes?
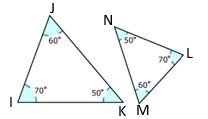Figura\(\PageIndex{8}\)Solución
Primero, comprueba si los dos triángulos son del mismo tamaño.
No
A continuación, comprueba si los dos triángulos tienen la misma forma.
Sí
Después, determine si los dos triángulos son similares o congruentes.
Similares
Los dos triángulos son similares.
Revisar
Utilice las siguientes figuras para responder a cada pregunta.
- ¿Estos dos triángulos son similares o congruentes?
- ¿Cómo lo sabes?
- ¿A qué lado es congruente\(\overline{AB}\)?
- ¿A qué lado es congruente\(\overline{AC}\)?
- ¿A qué lado es congruente\(\overline{RS}\)?
- ¿Qué ángulo es congruente con el ángulo A?
- ¿Qué ángulo es congruente con el ángulo B?
- ¿Qué ángulo es congruente con el ángulo C?
- ¿Las dos figuras son similares o congruentes?
- ¿Por qué?
- ¿A qué lado es congruente\(\overline{NO}\)?
- ¿A qué lado es congruente\(\overline{MN}\)?
- ¿A qué lado es congruente\(\overline{ST}\)?
- ¿A qué lado es congruente\(\overline{QT}\)?
- ¿A qué lado es congruente\(\overline{OP}\)?
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 9.17.
Recursos
El vocabulario
| Término | Definición |
|---|---|
| Congruente | Las figuras congruentes son idénticas en tamaño, forma y medida. |
| Correspondiente | Los lados correspondientes entre dos triángulos son lados en la misma posición relativa. |
| Similares | Dos figuras son similares si tienen la misma forma, pero no necesariamente del mismo tamaño. |
Recursos adicionales
Video: Triángulos Congruentes y Similares
Práctica: Partes correspondientes de figuras similares