9.4: Superficie
- Page ID
- 107320
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Superficie y redes
En geometría, una red es una forma bidimensional que se puede plegar para formar una forma tridimensional o un sólido. O una red es un dibujo hecho cuando la superficie de una figura tridimensional se presenta plana mostrando cada cara y borde de la figura en 2 dimensiones.
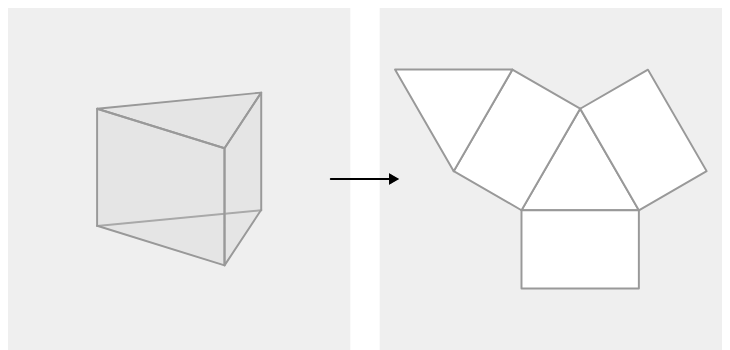
Aquí hay algunos pasos para determinar si una red forma un sólido:
1. Asegúrese de que el sólido y la red tengan el mismo número de caras y que las formas de las caras del sólido coincidan con las formas de las caras correspondientes en la red.
2. Visualice cómo se va a plegar la red para formar el sólido y asegúrese de que todos los lados encajen correctamente.
Las redes son útiles cuando necesitamos encontrar la superficie de los sólidos. En la imagen de arriba, se puede ver un prisma triangular cuando se despliega consiste en dos triángulos y tres rectángulos. Los triángulos son las bases del prisma y los rectángulos son las caras laterales.
Área de superficie de un sólido
El área superficial de un objeto tridimensional es la medida del área total de todas sus caras. Esto significa que una forma de encontrar la superficie de un sólido es encontrar el área de su red.
\(Surface\: area\: of\: rectangular\: prism=2ab+2ac+2bc=2(ab+ac+bc)\)
El área superficial de un prisma rectangular es el área de los seis rectángulos que lo cubren. Pero no tenemos que averiguar los seis porque sabemos que la parte superior e inferior son iguales, la parte delantera y trasera son iguales, y los lados izquierdo y derecho son los mismos.
Redes de Sólidos
Explore las redes y vea cómo la forma 2d se transforma en una forma 3d.

Tenga en cuenta que podría haber un par de interpretaciones diferentes de cualquier red. La mayoría de los prismas tienen múltiples redes.
Elemento Interactivo
Agrega el texto del elemento interactivo aquí. Esta caja NO se imprimirá en pdf
Encuentra el área de superficie aproximada del prisma triangular a continuación. La base es un triángulo equilátero.
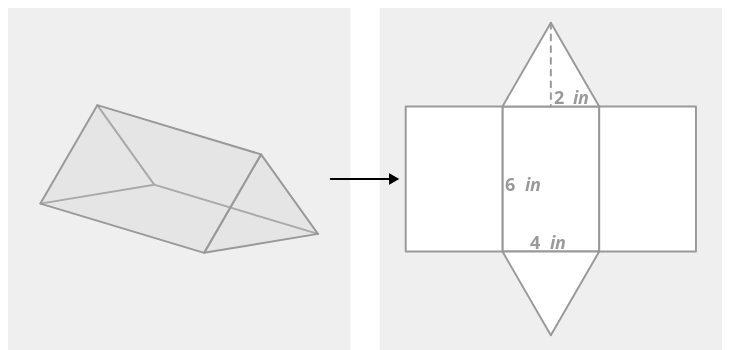
La red está compuesta por tres rectángulos congruentes y dos triángulos equiláteros congruentes.
El área superficial es la suma de las áreas de las cinco formas. Para encontrar el área del triángulo, es necesario conocer la altura del triángulo. Utilizando el Teorema de Pitágoras, se puede determinar que la altura es de aproximadamente 3.46 pulgadas.
\(H^2=P^2+B^2\)
\(4^2=P^2+2^2\)
\(P^2=16−4=12\)
\(P=3.46 inches\)

Dibuja la red de una pirámide cuadrada.
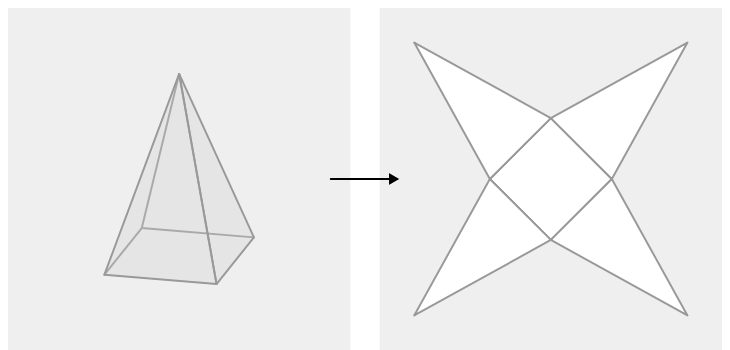
Una pirámide cuadrada tiene una altura de 20 pulgadas. Cada lado de la base cuadrada mide 12 pulgadas. ¿Cuál es la superficie de la pirámide?
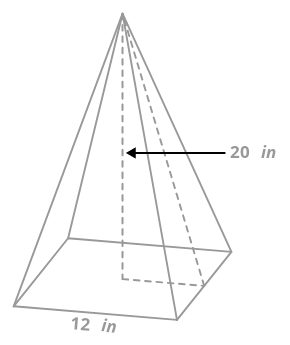
Para encontrar el área de superficie, deberá determinar el área de las caras triangulares. Para encontrar el área de cada cara triangular, necesitarás la base y la altura del triángulo. Para ello, imagina un triángulo rectángulo erguido en la pirámide.
La altura de este triángulo es de 20 pulgadas y la base del triángulo es de 6 pulgadas. Es hipotenusa, que es la altura de la cara triangular, se puede determinar con el Teorema de Pitágoras.
Ahora puedes encontrar el área de cada una de las cinco formas que componen la red con el fin de encontrar la superficie.

\(H^2=P^2+B^2\)
\(H^2=20^2+6^2\)
\(H^2=400+36\)
\ (H=\ sqrt {436} =20.88 pulgadas

Identificar el sólido cuya red se da a continuación, con base en la forma de la base.
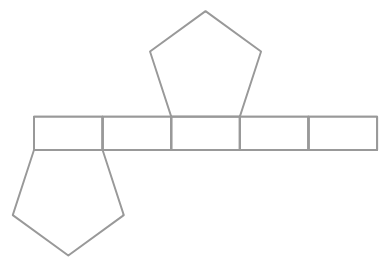
El sólido es _______.
CK-12 PLIX: Secciones Transversales y Redes
Elemento Interactivo
Ejemplo\(\PageIndex{1}\)
Una taza de pintura cubre aproximadamente 22 pies cuadrados. Necesitas pintar todas las caras de un cubo para usarlo como utilería en una obra de teatro. Cada borde del cubo mide 2.5 pies de largo. ¿Cuánta pintura necesitarás comprar?
Solución
Una taza de pintura cubre aproximadamente 22 pies cuadrados. Cada borde del cubo mide 2.5 pies de largo. Para averiguar cuánta pintura necesitarás, debes encontrar el área de superficie del cubo.
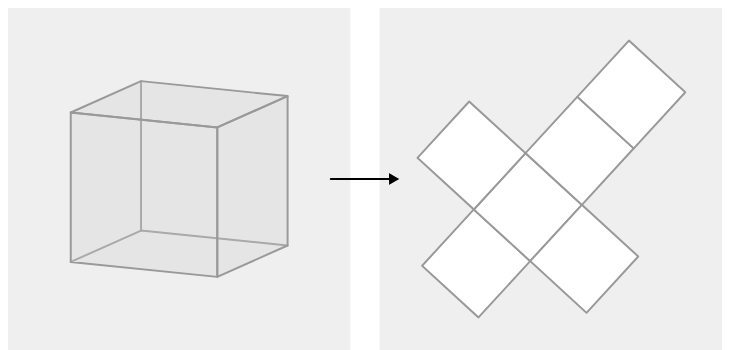
El cubo tiene seis caras cuadradas congruentes. El área de cada cuadrado es\((2.5)^2=6.25 ft^2\). La superficie total del cubo es\(37.5 ft^2\). Necesitarás\(37.522\approx 1.7\) tazas de pintura.
Ejemplo\(\PageIndex{2}\)
Dibuja la red para un prisma pentagonal.
Solución
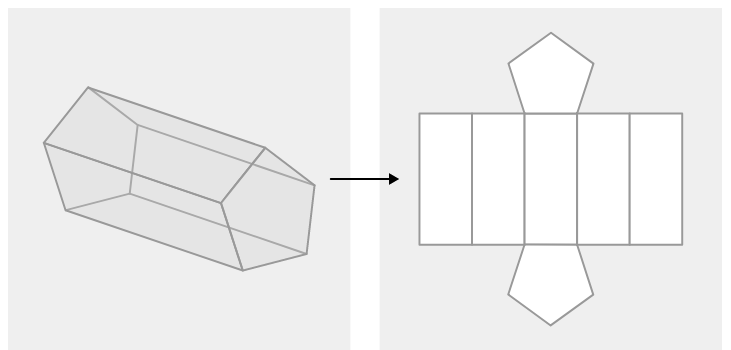
Ejemplo\(\PageIndex{3}\)
La base de un prisma pentagonal es el siguiente pentágono:
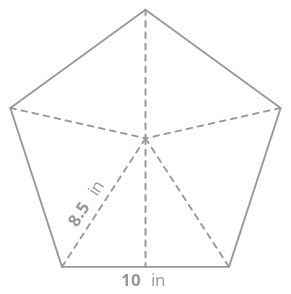
Encuentra el área del pentágono diseccionando el pentágono en cinco triángulos y encontrando el área de cada triángulo.
Solución
Usa el Teorema de Pitágoras para encontrar la altura de cada triángulo.
\(H^2=P^2+B^2\)
\(8.5^2=P^2+5^2\)
\(P^2=72.25−25=47.25\)
\(P=\sqrt{47.25}=6.87 inches\)

Ejemplo\(\PageIndex{4}\)
Encuentra el área de superficie para un prisma pentagonal con una altura de 25 pulgadas y una base dada en el Ejemplo 3.

Solución
El prisma pentagonal está formado por cinco caras rectangulares y dos caras pentagonales. Cada rectángulo mide 10 pulgadas por 25 pulgadas.

Revisar
1. Explicar la conexión entre el área superficial de un sólido y la red de un sólido.
2. Al indicar un área de superficie, ¿por qué se utilizan unidades cuadradas como\(in^2\) "”?
Una pirámide triangular tiene cuatro caras triangulares equiláteros congruentes. Cada borde de la pirámide mide 6 pulgadas.
3. Dibuja una red para la pirámide.
4. Encuentra el área de una cara triangular.
5. Encuentra la superficie de la pirámide.
Una pirámide hexagonal de 20 pulgadas de alto tiene una base hexagonal regular que se puede dividir en seis triángulos equiláteros con longitudes laterales de 12 pulgadas, como se muestra a continuación.
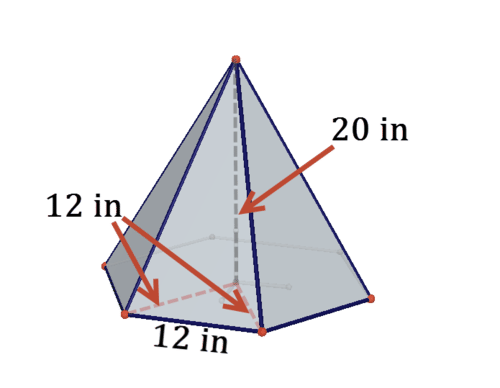
6. Dibuja una red para la pirámide.
7. Encuentra el área de la base hexagonal.
8. La pirámide tiene 6 caras triangulares. Usa el Teorema de Pitágoras para ayudarte a encontrar la altura de cada uno de estos triángulos.
9. Encuentra la superficie total de la pirámide.
Un prisma cuadrado se remata con una pirámide cuadrada para crear el sólido compuesto debajo.
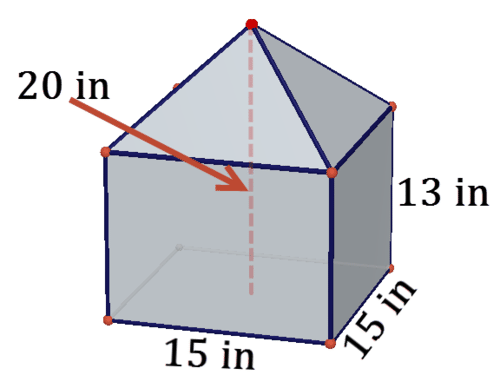
10. Dibuja una red para el sólido.
11. Hay cuatro caras triangulares. Usa el Teorema de Pitágoras para ayudarte a encontrar la altura de cada uno de estos triángulos.
12. Encuentra la superficie total del sólido.
Un sólido tiene la siguiente neta.
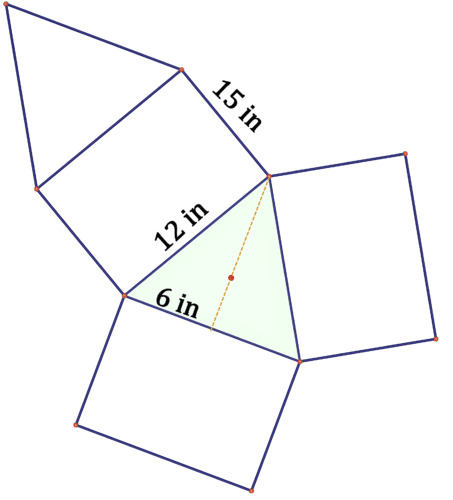
13. ¿Qué tipo de sólido es este?
14. Encuentra el área de superficie del sólido.
15. ¿Cómo sería la red de un cilindro? Intenta hacer un boceto.
16. ¿Cómo sería la red de un cono? Intenta hacer un boceto.
16. Grafica los puntos\((2,3)\) y\((12,3)\). Etiquételos A y B y conéctelos para formar un segmento. Dibuje segmentos verticales conectándolos al\(x\) eje. Gire esta forma alrededor del\(x\) eje para formar un sólido. ¿Qué cifra has hecho? Explique. Encuentra la superficie y el volumen de esta figura.
17. Grafica los puntos\((2,0)\) y\((10,6)\). Etiquételos A y B y conéctelos para formar un segmento. Dibuja un segmento vertical desde B hasta el\(x\) eje. Gire esta forma alrededor del\(x\) eje para formar un sólido. ¿Qué cifra has hecho? Explique. Encuentra la superficie y el volumen de esta figura.
18. Grafica los puntos\((24,10)\) y\((12,5)\). Formar un sólido de revolución como se describió anteriormente. Encuentra su superficie y volumen.
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 1.11.
Recursos adicionales
Elemento Interactivo
Práctica: Superficie

