9.5: Volumen

Número de cubos unitarios para llenar prismas, esferas, pirámides, cilindros, conos y sólidos compuestos.

Volumen de Sólidos

El volumen de un sólido es la medida de cuánto espacio ocupa un objeto. Se mide por el número de cubos unitarios que se necesitan para llenar el sólido.

Figura$\PageIndex{1}$

Volumen de un prisma

Un prisma es un sólido con dos bases poligonales congruentes que son paralelas y conectadas por rectángulos. Los prismas son nombrados por su forma base.

Figura$\PageIndex{2}$

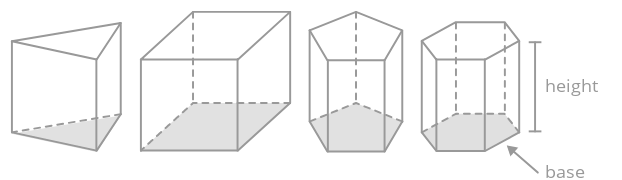
Para encontrar el volumen de un prisma, encuentra el área de su base y multiplícalo por su altura.
$V_{prism}=A_{base}\cdot h$

Volumen de un cilindro

Un cilindro es un sólido tridimensional que consta de dos lados congruentes, paralelos y circulares (las bases), unidos por una superficie curva.

Figura$\PageIndex{3}$

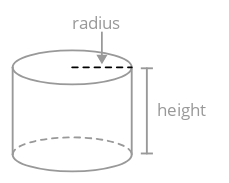
Para encontrar el volumen de un cilindro, encontrar el área de su base circular y multiplicar por su altura.

$V_{cylinder}= \pir^{2}h$

CK-12 PLIX: Superficie y Volumen de Cilindros

Elemento Interactivo

Volumen de una pirámide

Una pirámide es un sólido tridimensional con una base poligonal. Cada esquina de un polígono está unida a un vértice singular, lo que le da a la pirámide su forma distintiva. Cada borde base y el vértice forman un triángulo. Las pirámides son nombradas por su forma base.

Para encontrar el volumen de una pirámide, encuentra el volumen del prisma con la misma base y divídalo por tres.

Figura$\PageIndex{4}$

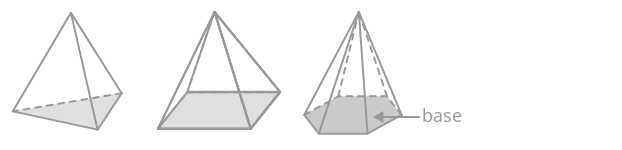
$V_{pyramid}=\dfrac{A_{base}\cdot h}{3}$

Volumen de un Cono

Un cono es un sólido tridimensional con una base circular cuya superficie lateral se encuentra en un punto llamado vértice.

Figura$\PageIndex{5}$

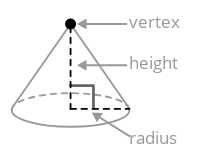
Para encontrar el volumen de un cono, encuentra el volumen del cilindro con la misma base y divídalo por tres.

$V_{cone}=\dfrac{ \pi r^{2}h}{3}$

Considerar:

¿Cuál es la relación entre el volumen de un cilindro y de un cono, teniendo el mismo radio y altura?

Figura$\PageIndex{6}$

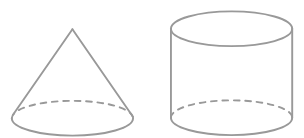
La relación entre el volumen de un cilindro y un cono con el mismo radio y altura es _______.

Volumen de una Esfera

Una esfera es el conjunto de todos los puntos en el espacio equidistante de un punto central. La distancia desde el punto central a la esfera se llama radio.

Figura$\PageIndex{7}$

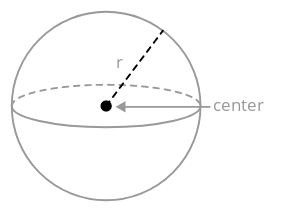
El volumen de una esfera depende de su radio.

$V_{sphere}=\dfrac{4}{3} \pi r^{3}$

Cálculo del volumen

Haga clic en la pequeña flecha azul junto a la imagen de abajo y arrastre los puntos naranjas para ajustar las dimensiones del sólido que se indican a continuación y observar cómo cambia el volumen.

Figura\(\PageIndex{8}\)

Volumen de un sólido compuesto

Un sólido compuesto es un sólido compuesto por sólidos geométricos comunes. Los sólidos que lo componen son generalmente prismas, pirámides, conos, cilindros y esferas.

Figura$\PageIndex{8}$

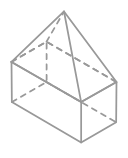
El volumen de un sólido compuesto es la suma de los volúmenes de los sólidos individuales que componen el compuesto.

Veamos algunos problemas donde encontramos el volumen.

1. Encuentra el volumen del prisma rectangular a continuación.

Figura$\PageIndex{9}$

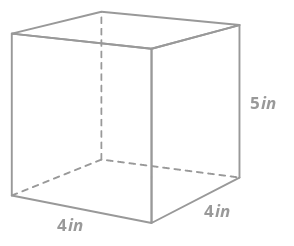
Para encontrar el volumen del prisma, es necesario encontrar el área de la base y multiplicar por la altura. Tenga en cuenta que para un prisma rectangular, cualquier cara puede ser la “base”, no solo la cara que parece estar en la parte inferior.

Figura$\PageIndex{10}$

2. Encuentra el volumen del cono a continuación.

Figura$\PageIndex{11}$

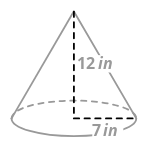
Para encontrar el volumen del cono, es necesario encontrar el área de la base circular, multiplicar por la altura y dividir por tres.

Figura$\PageIndex{12}$

3. Encuentra el volumen de una esfera con radio de 4 cm.

Figura$\PageIndex{11}$

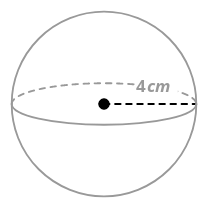
$\begin{aligned} \text{Volume of Sphere }&=&\dfrac{4}{3} \pi r^{3} \\ &=&\dfrac{4}{3} \pi(4)^{3} \\ &=&\dfrac{256 \pi}{3} cm^{3}\end{aligned}$

Ejemplo$\PageIndex{1}$

El sólido compuesto de abajo está hecho de un cubo y una pirámide cuadrada. La longitud de cada borde del cubo es de 12 pies y la altura total del sólido es de 22 pies. ¿Cuál es el volumen del sólido? ¿Por qué querrías conocer el volumen del sólido?

Figura$\PageIndex{1}$

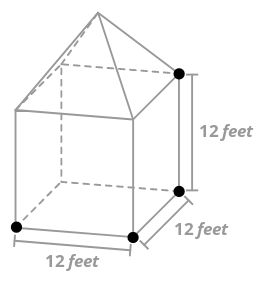
Solución

Para encontrar el volumen del sólido, encuentra la suma de los volúmenes del prisma (el cubo) y la pirámide. Tenga en cuenta que dado que la altura total es de 22 pies y la altura del cubo es de 12 pies, la altura de la pirámide debe ser de 10 pies.

\ (\ begin {alineado}
\ text {Volumen de prisma (Cubo)} &=A_ {\ text {base}}\ cdot h\\
& =( 12\ cdot 12) (12)\\
&=1728\ mathrm {ft} ^ {3}\
\ text {Volumen de Pirámide} &=\ frac {A_ {\ texto {base}}\ cdot h} {3}\\
&=\ frac {(12\ cdot 12) (10)} {3}\\
&=480\ mathrm {ft} ^ {3}\\
&=\ text {Volumen de prisma (Cubo)} +\ text {Volumen de Pirámide}\\
&=1728+480\\
&=2208\ mathrm {ft} ^ {3}
\ end {alineado}\)

El volumen te ayuda a saber cuánto aguantará el sólido. Un pie cúbico contiene aproximadamente 7.48 galones de líquido, por lo que

\ (\ begin {aligned}
\ text {Galones de líquido el sólido puede contener} &=\ text {Volumen de sólido. Número de galones/pie cúbico}\\
& =( 2208) (7.48)\\
&=16,515.84\ text {galones}
\ end {alineado}\)

Ejemplo$\PageIndex{2}$

El área de la base de la pirámide de abajo es$100 cm^{2}$. La altura es de 5 cm. ¿Cuál es el volumen de la pirámide?

Figura$\PageIndex{12}$

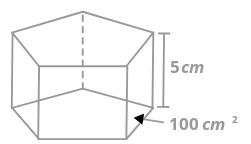
Solución

$V_{prism}=A_{base}\cdot h=(100\text{ cm}^{2} )\cdot (5 cm)=500\text{ cm}^{3}$

Ejemplo$\PageIndex{3}$

El volumen de una esfera es$\dfrac{500 \pi}{3} in^{3}$. ¿Cuál es el radio de la esfera?

Solución

Para encontrar el radio, utilice la fórmula:$Volume\: of\: Sphere = \dfrac{4}{3} \pir^{3}$

$\begin{aligned} \dfrac{500 \pi}{3}&=\dfrac{4}{3} \pi r^{3} \\ 4r^{3} =500 \\ r^{3} &=125 \\ r&=5\text{ in} \end{aligned}$

Ejemplo$\PageIndex{4}$

El volumen de una pirámide cuadrada es$64 in^{3}$. La altura de la pirámide es tres veces la longitud de un lado de la base. ¿Cuál es la altura de la pirámide?

Solución

Figura$\PageIndex{13}$

Lateral$s=4$ adentro y altura$h=3(4)=12 in.$

Revisar

Encuentra el volumen de cada sólido o sólido compuesto.

1. 
   

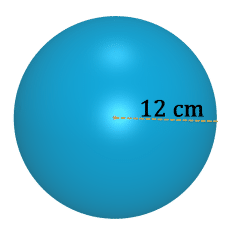
   Figura$\PageIndex{14}$

2. 
   

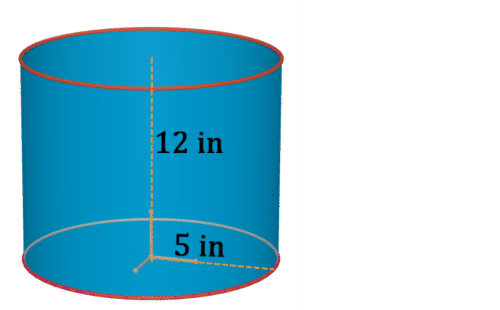
   Figura$\PageIndex{15}$

3. 
   

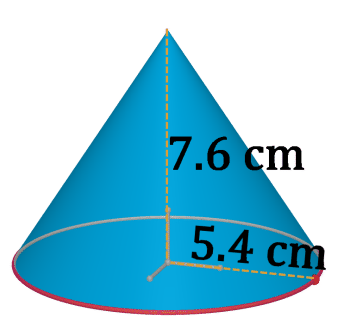
   Figura$\PageIndex{16}$

4. 
   

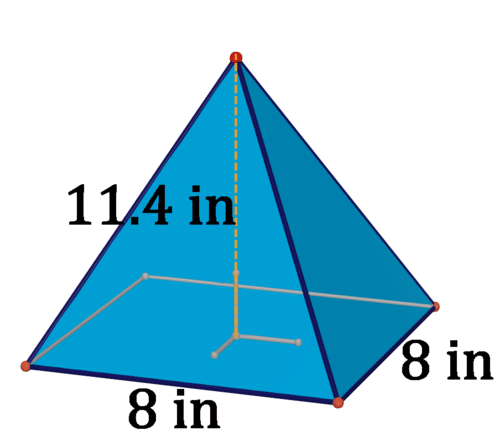
   Figura$\PageIndex{17}$

5. La base es un triángulo equilátero.

   
   

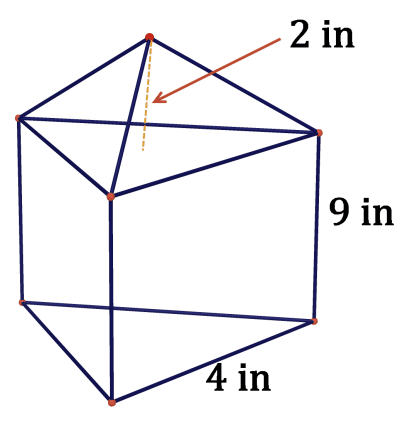
   Figura$\PageIndex{18}$

6. 
   

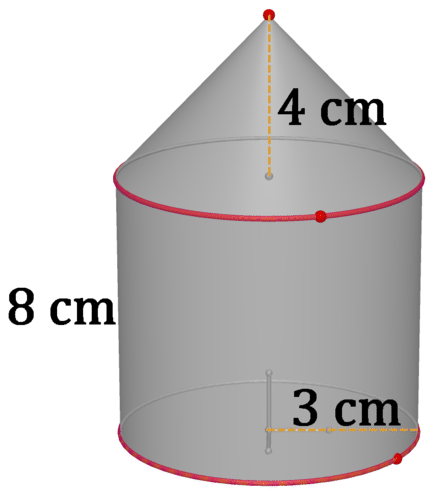
   Figura$\PageIndex{19}$

7. Explique por qué la fórmula para el volumen de un prisma involucra el área de la base.

8. ¿Cómo se relaciona un cilindro con un prisma?

9. ¿Cómo se relaciona una pirámide con un cono?

10. ¿Cómo se relaciona una esfera con un círculo?

11. Si un centímetro cúbico contendrá 1 mililitro de agua, aproximadamente ¿cuántos litros de agua aguantará el sólido en #1? (Un litro son 1000 mililitros).

12. Si un centímetro cúbico contendrá 1 mililitro de agua, aproximadamente ¿cuántos litros de agua aguantará el sólido en #3? (Un litro son 1000 mililitros).

13. Si 231 pulgadas cúbicas contendrán un galón de agua, aproximadamente ¿cuántos galones de agua sostendrá el sólido en #5?

14. El volumen de un cono es$125 \pi in^3$. La altura es tres veces la longitud del radio. ¿Cuál es la altura del cono?

15. El volumen de un prisma pentagonal es$360 in^3$. La altura del prisma es de 3 pulgadas. ¿Cuál es el área de la base del pentágono?

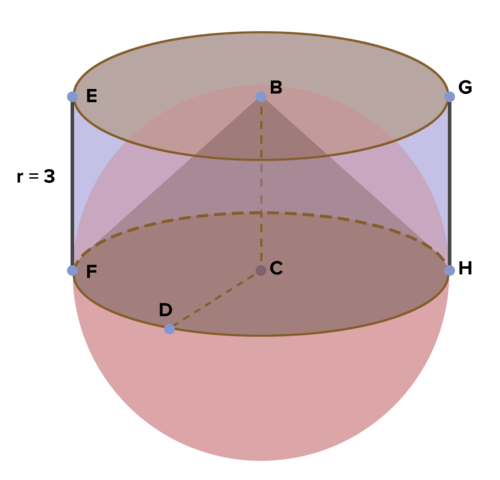
16. La siguiente figura presenta un cilindro cuya altura es de 3 unidades. Dentro del cilindro hay un hemisferio (la mitad de una esfera). Y dentro del hemisferio hay un cono. Encuentra el volumen del cilindro y el cono. Encuentra el volumen de la esfera y luego el hemisferio. ¿Ves una relación entre el volumen del cilindro y el cono, y el del hemisferio? Explique. Utilice esto para derivar la fórmula para el volumen de una esfera a partir de las fórmulas para un cilindro y un cono.

Figura$\PageIndex{20}$

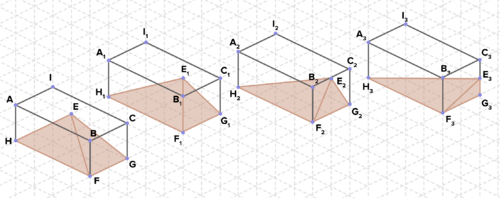
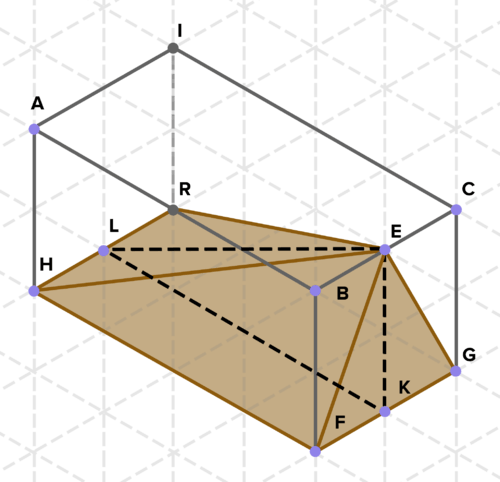
17. La rejilla isométrica de abajo está compuesta por triángulos equiláteros cuyo lado son de longitud unitaria 1. Encuentra el volumen para cada una de las pirámides. ¿Qué observas? Explique.

Figura$\PageIndex{21}$

18. Encuentra el área de superficie y volumen de la siguiente pirámide. Cada segmento de línea en la cuadrícula de fondo tiene una longitud 1.

Figura$\PageIndex{22}$

Reseña (Respuestas)

Para ver las respuestas de la opinión, haga clic aquí.