9.6: Secciones Transversales y Sólidos Básicos de Revolución
- Page ID
- 107272
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Secciones transversales de sólidos y sólidos creados por rotación de formas alrededor de líneas.
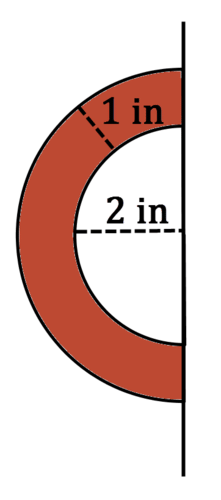
La figura sombreada de abajo se gira alrededor de la línea. ¿Cuál es el volumen del sólido que se crea?
Secciones Transversales
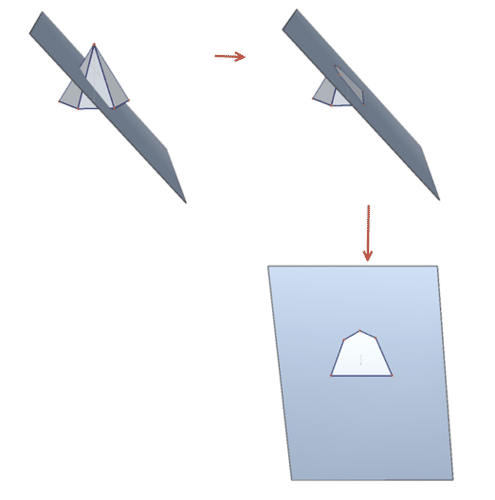
Recordemos que una sección transversal es la forma que ves cuando haces una rebanada a través de un sólido. Un sólido puede tener muchas secciones transversales diferentes dependiendo de dónde se haga la rebanada. Considera una pirámide hexagonal. Las secciones transversales perpendiculares a la base serán triángulos. Las secciones transversales paralelas a la base serán hexágonos. También es posible tomar secciones transversales utilizando planos que no son paralelos ni perpendiculares a la base. Abajo, una pirámide hexagonal ha sido cortada en una inclinación. La sección transversal es un pentágono.
Elemento Interactivo
Agrega el texto del elemento interactivo aquí. Esta caja NO se imprimirá en pdf
Las secciones transversales son una forma en que los objetos bidimensionales se conectan a objetos tridimensionales.
Una segunda conexión entre dos y tres dimensiones proviene del hecho de que los sólidos tridimensionales se pueden crear girando objetos bidimensionales alrededor de una línea.
Elemento Interactivo
Agrega el texto del elemento interactivo aquí. Esta caja NO se imprimirá en pdf
Veamos algunos problemas sobre las secciones transversales.
- Identifique el sólido que se crea cuando la siguiente forma se gira alrededor de la línea.
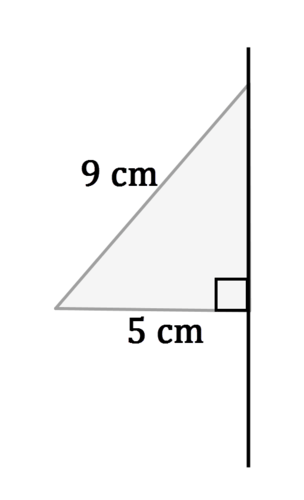
El sólido es un cono con radio de 5 cm.
- Encuentra el volumen del sólido de #1.
El volumen de un cono es\(V=\dfrac{\pi r^{2}h}{3}\). El radio es de 5 cm. Para encontrar la altura del cono, usa el Teorema de Pitágoras:
\(5^{2}+h^{2}=9^{2}\)
\(h=\sqrt{56}\approx 7.48\: cm\)
El volumen del cono es:
\(V=\dfrac{\pi (5^{2})(7.48)}3\approx 195.83 cm^{3}\)
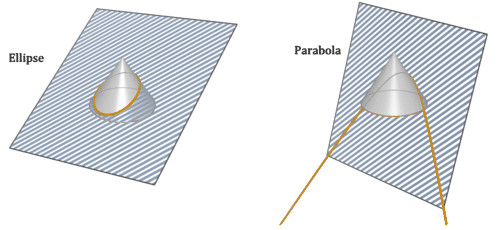
- Identificar al menos tres formas bidimensionales creadas por secciones transversales del sólido desde el primer problema.
Las secciones transversales tomadas paralelas a la base serán círculos. Las secciones transversales tomadas perpendiculares a la base serán triángulos. Cuando la sección transversal se toma en una inclinación, hay muchas otras posibilidades. Dos secciones transversales adicionales son una elipse o una parábola rellena.
Ejemplo\(\PageIndex{1}\)
Anteriormente, se le preguntó cuál es el volumen del sólido que se creó.
La figura sombreada de abajo se gira alrededor de la línea.

Solución
El sólido resultante es una esfera con una esfera quitada del centro. El volumen de la esfera grande es\(\dfrac{4\pi (3^{3})}{3}=36\pi in^{3}\). El volumen de la pequeña esfera es\(\dfrac{4\pi (2^{3})}{3}=32\pi 3 in^{3}\). El volumen del sólido resultante es:
\(V=36\pi −\dfrac{32\pi} {3}=\dfrac{76\pi}{3}\text{ in}^{3}\)
Usa la imagen de abajo para #2 - #4.
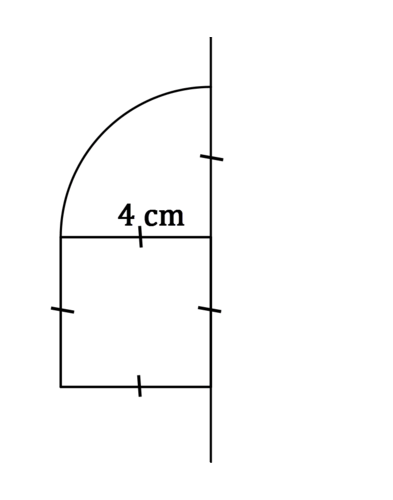
Ejemplo\(\PageIndex{2}\)
Identificar el sólido que se crea cuando la figura anterior se gira alrededor de la línea.
Solución
El sólido es un cilindro con un hemisferio en la parte superior. El radio de cada uno es de 4 cm.
Ejemplo\(\PageIndex{3}\)
Encuentra el volumen del sólido de #2.
Solución
El volumen del cilindro es\(\pi (4^{2})(4)=64\pi cm^{3}\). El volumen del hemisferio es\(\dfrac{4\pi (4^{3})}{6}=\dfrac{128\pi}{3} cm^{3}\). El volumen de todo el sólido es\(\dfrac{320\pi}{3} cm^{3}\).
Ejemplo\(\PageIndex{4}\)
Identificar al menos tres formas bidimensionales creadas por secciones transversales del sólido a partir de #2.
Solución
Posibles respuestas: Las secciones transversales tomadas paralelas a la base serán círculos. Las secciones transversales tomadas perpendiculares a la base serán rectángulos con semicírculos en la parte superior. Algunas secciones transversales tomadas en una inclinación serán elipses.
Revisar
Usa la imagen de abajo para #1 - #3.
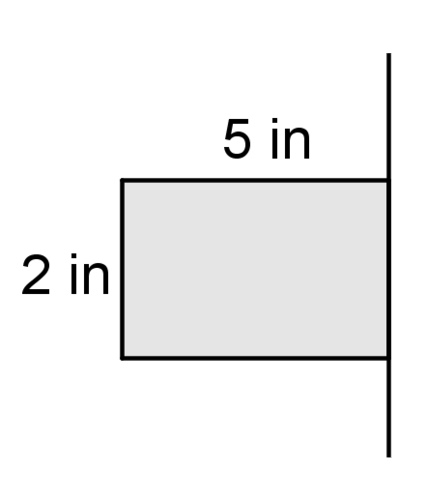
1. Describa el sólido que se crea cuando la figura anterior se gira alrededor de la línea.
2. Encuentra el volumen del sólido.
3. Identificar al menos 3 formas bidimensionales creadas por secciones transversales del sólido.
Usa la imagen de abajo para #4 - #6.
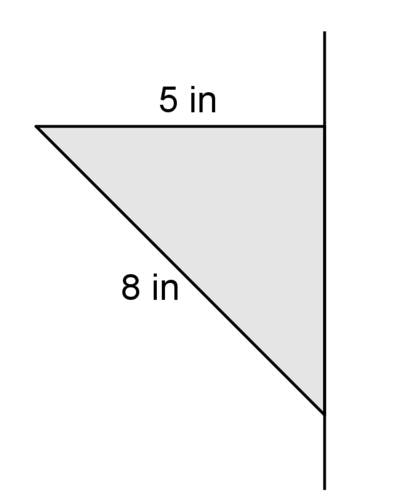
4. Describa el sólido que se crea cuando la figura anterior se gira alrededor de la línea.
5. Encuentra el volumen del sólido.
6. Identificar al menos 3 formas bidimensionales creadas por secciones transversales del sólido.
Usa la imagen de abajo para #7 - #9.
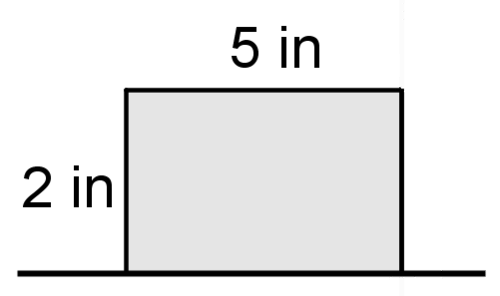
7. Describa el sólido que se crea cuando la figura anterior se gira alrededor de la línea.
8. Encuentra el volumen del sólido.
9. Identificar al menos 2 formas bidimensionales creadas por secciones transversales del sólido.
Usa la imagen de abajo para #10 - #12.
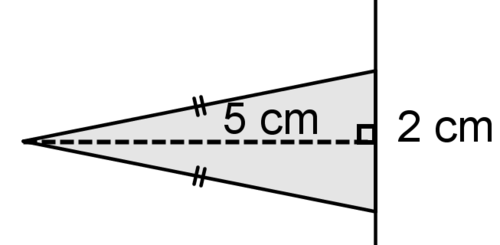
10. Describa el sólido que se crea cuando la figura anterior se gira alrededor de la línea.
11. Encuentra el volumen del sólido.
12. Identificar al menos 2 formas bidimensionales creadas por secciones transversales del sólido.
Usa la imagen de abajo para #13 - #15.
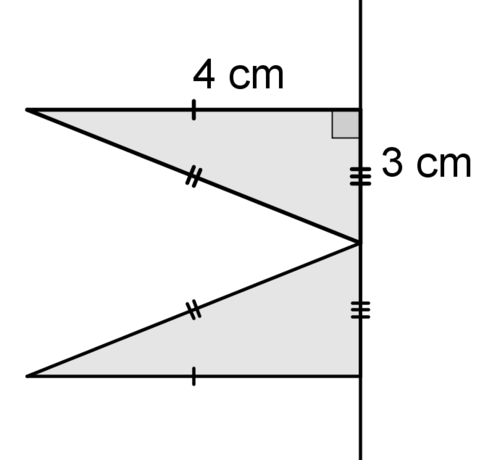
13. Describa el sólido que se crea cuando la figura anterior se gira alrededor de la línea.
14. Encuentra el volumen del sólido.
15. Identificar al menos 2 formas bidimensionales creadas por secciones transversales del sólido.
16. A continuación se presentan secciones transversales de diversos sólidos. Encuentra el área de cada sección transversal. (En el papel de rejilla isométrico que se muestra, un lado de un triángulo equilátero representa 1 unidad de longitud en cualquier dirección).
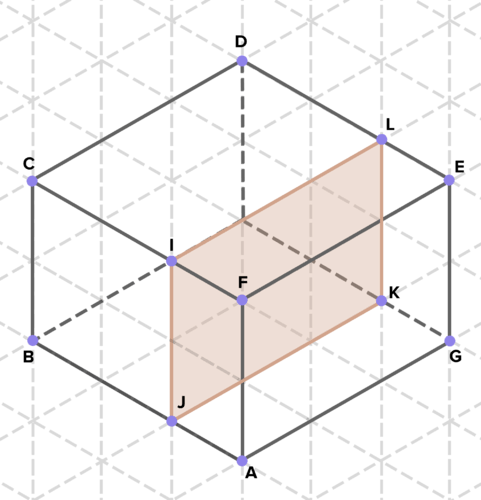
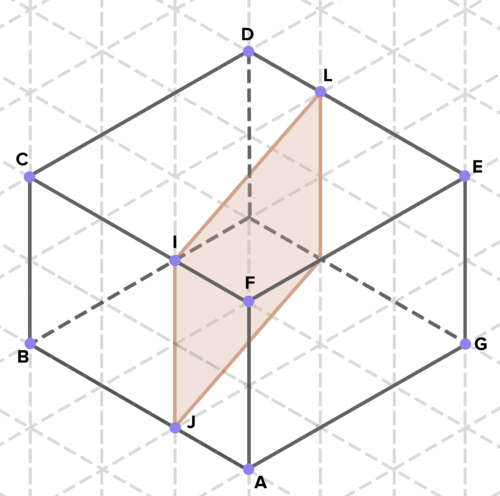
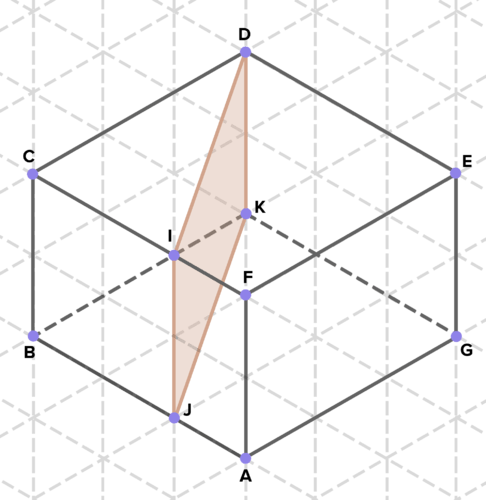
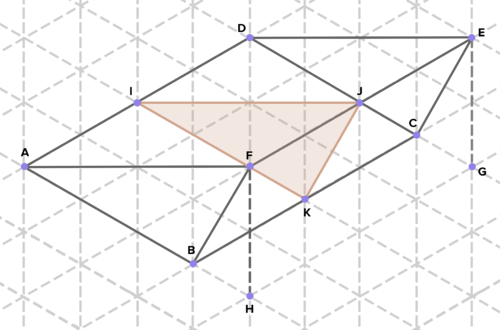
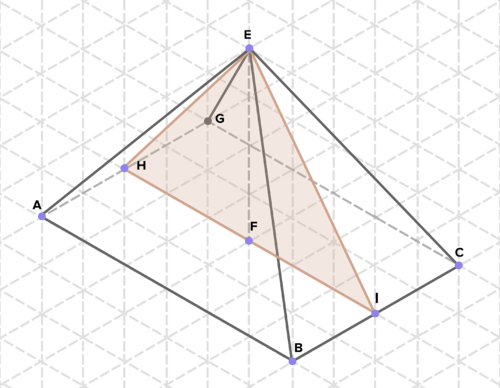
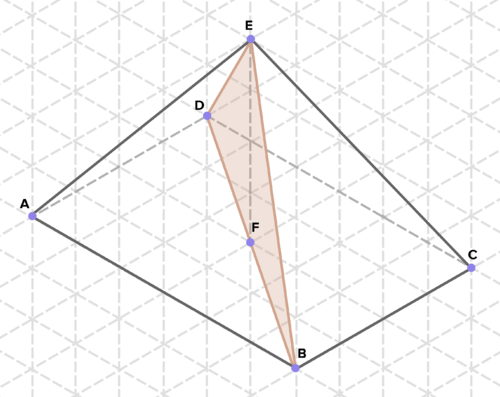
Reseña (Respuestas)
Para ver las respuestas de la opinión, haga clic aquí.

