9.7: Sólidos compuestos
- Page ID
- 107282
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Sólidos compuestos por dos o más sólidos.
Un sólido compuesto es un sólido que está compuesto, o compuesto por, dos o más sólidos. Los sólidos de los que se compone son generalmente prismas, pirámides, conos, cilindros y esferas. Para encontrar el área superficial y el volumen de un sólido compuesto, es necesario saber cómo encontrar el área superficial y el volumen de prismas, pirámides, conos, cilindros y esferas. Para mayor información sobre cualquiera de esos sólidos específicos, consulte el concepto que se enfoca en ellos. Este concepto asumirá el conocimiento de esos cinco sólidos.
La mayoría de los problemas de sólidos compuestos que verá serán sobre el volumen, por lo que la mayoría de los ejemplos y problemas de práctica a continuación son sobre el volumen. También hay un ejemplo de área de superficie.
¿Y si construyeras un modelo sólido de casa tridimensional que consiste en una pirámide encima de un prisma cuadrado? ¿Cómo podría determinar cuánto espacio bidimensional y tridimensional ocupa ese modelo?
Ejemplo\(\PageIndex{1}\)
Encuentra el volumen del siguiente sólido.
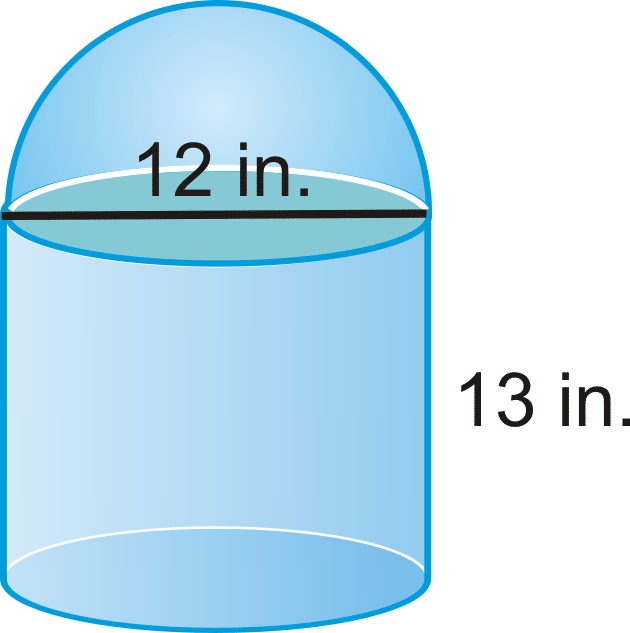
Solución
Usa lo que sabes de cilindros y esferas. La parte superior del sólido es un hemisferio.
\(\begin{aligned} V_{cylinder}&= \pi 6^{2}(13)=468 \pi \\ V_{hemisphere}&=12(\dfrac{4}{3} \pi 6^{3})=144 \pi \\ V_{total}&=468 \pi +144 \pi =612 \pi \text{ in}^{3} \end{aligned}\)
Ejemplo\(\PageIndex{2}\)
Encuentra el volumen del prisma base. Redondea tu respuesta a la centésima más cercana.
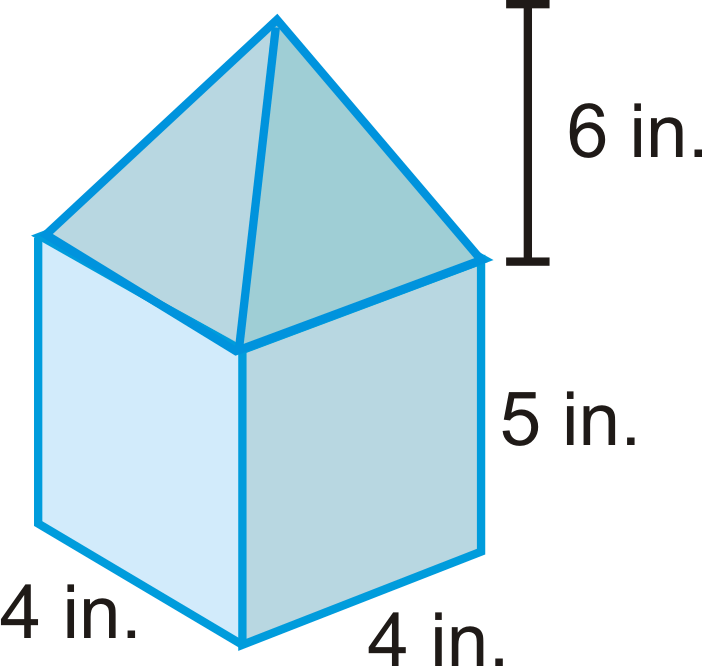
Solución
Usa lo que sabes de los prismas.
\(\begin{aligned} V_{prism}=B\cdot h \\ V_{prism}=(4\cdot 4)\cdot 5 \\ V_{prism}=80\text{ in}^{3}\end{aligned}\)
Ejemplo\(\PageIndex{3}\)
Encuentra el volumen del sólido a continuación.
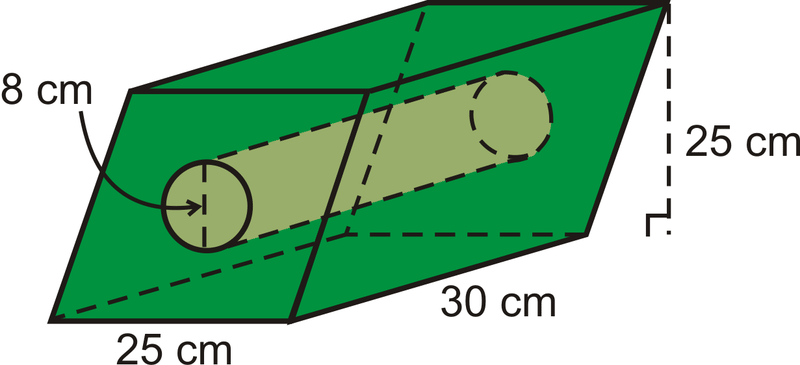
Solución
Este sólido es un prisma basado en paralelogramo con un cilindro cortado en el centro.
\(\begin{aligned} V_{prism}=(25\cdot 25)30=18,750\text{ cm}^{3} \\ V_{cylinder}= \pi (4)^{2}(30)=480 \pi \text{ cm}^{3}\end{aligned}\)
El volumen total es\(18750−480 \pi \approx 17,242.04 cm^{3}\).
Ejemplo\(\PageIndex{4}\)
Encuentra el volumen del sólido compuesto. Todas las bases son cuadrados.
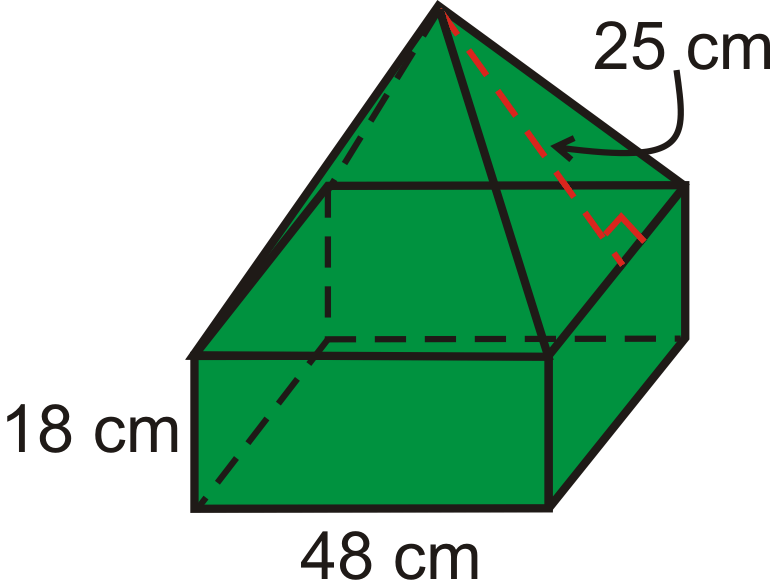
Solución
Se trata de un prisma cuadrado con una pirámide cuadrada en la parte superior. Primero, necesitamos la altura de la porción piramidal. Usando el Teorema de Pitágoras, tenemos,\(h=\sqrt{25^{2}−24^{2}}=7\).
\(\begin{aligned} V_{prism}&=(48)(48)(18)=41,472\text{ cm}^{3} \\ V_{pyramid}&=\dfrac{1}{3}(48^{2})(7)=5376\text{ cm}^{3}\end{aligned}\)
El volumen total es\(41,472+5376=46,848 cm^{3}\).
Ejemplo\(\PageIndex{5}\)
Encuentra el área de superficie del siguiente sólido.
Solución
Este sólido es un cilindro con un hemisferio en la parte superior. Es un sólido, por lo que no incluya la parte inferior del hemisferio ni la parte superior del cilindro.
\(\begin{aligned}SA&=LA_{cylinder}+LA_{hemisphere}+A_{base\: circle} \\ &=2 \pi rh+\dfrac{1}{2}4 \pi r^{2}+ \pi r^{2} \\ &=2 \pi (6)(13)+2 \pi 6^{2}+ \pi 6^{2} \\ &=156 \pi +72 \pi +36 \pi \\ &=264 \pi in^{2}\end{aligned}\)
“LA” significa área lateral.
Revisar
Redondea tus respuestas a la centésima más cercana. El sólido de abajo es un cubo con un cono recortado.
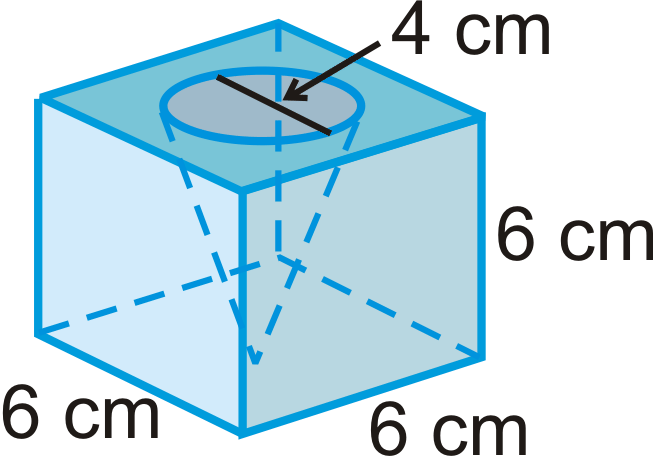
- Encuentra el volumen del cubo.
- Encuentra el volumen del cono.
- Encuentra el volumen de todo el sólido.
El sólido de abajo es un cilindro con un cono en la parte superior.
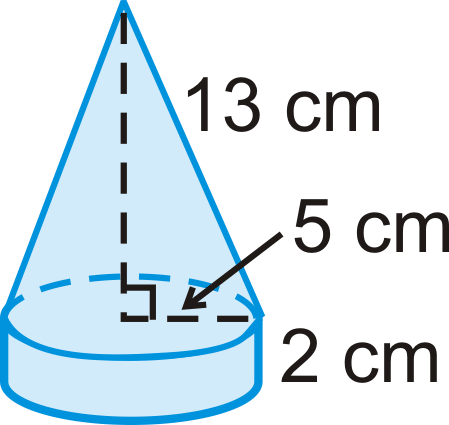
- Encuentra el volumen del cilindro.
- Encuentra el volumen del cono.
- Encuentra el volumen de todo el sólido.
-
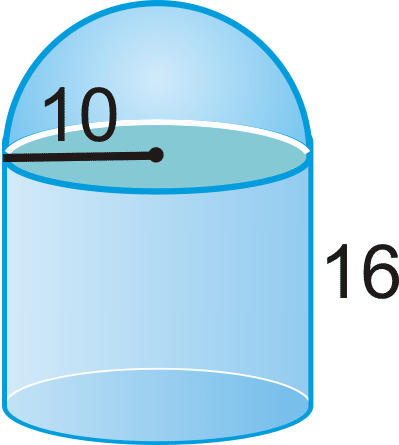
Figura\(\PageIndex{8}\) -
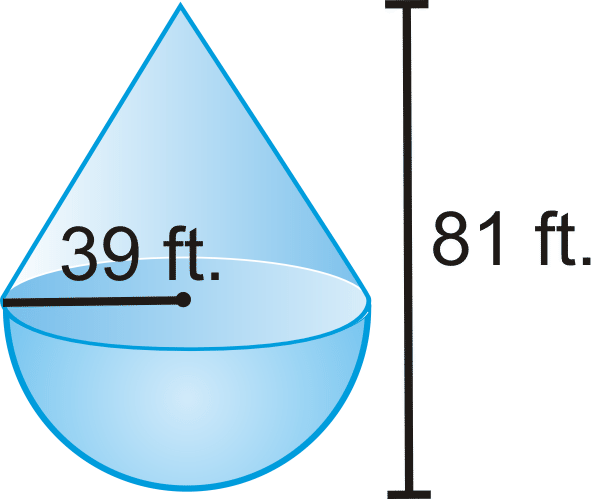
Figura\(\PageIndex{9}\) - Puedes asumir que el fondo está abierto.
Encuentra el volumen de las siguientes formas. Redondea tus respuestas a la centésima más cercana.
-
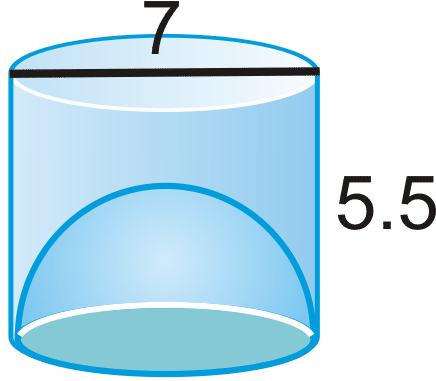
Figura\(\PageIndex{11}\) -
Figura\(\PageIndex{12}\) -
Figura\(\PageIndex{1}\): Copiar y Pegar Leyenda aquí. (Copyright; autor vía fuente) - Una esfera tiene un radio de 5 cm. Un cilindro derecho tiene el mismo radio y volumen. Encuentra la altura del cilindro.
Las bases del prisma son cuadradas y se corta un cilindro del centro.
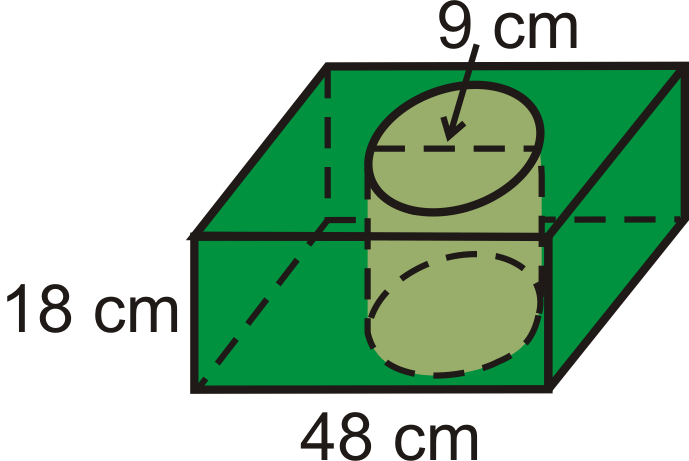Figura\(\PageIndex{13}\)- Encuentra el volumen del prisma.
- Encuentra el volumen del cilindro en el centro.
- Encuentra el volumen de la figura.
Se trata de un prisma con medio cilindro en la parte superior.
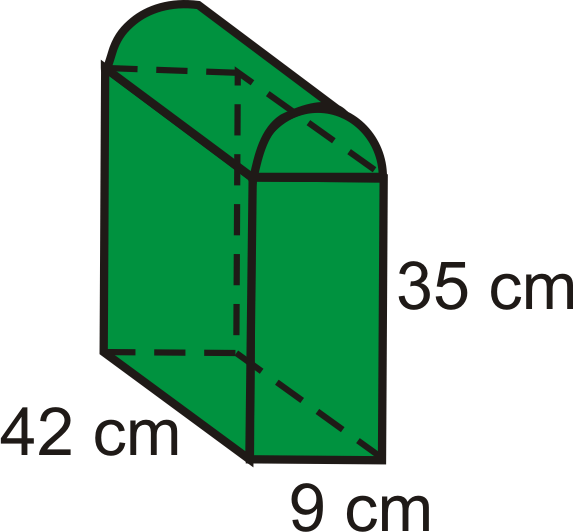Figura\(\PageIndex{14}\)- Encuentra el volumen del prisma.
- Encuentra el volumen del medio cilindro.
- Encuentra el volumen de toda la figura.
Las pelotas de tenis con un diámetro de 3 pulgadas se venden en latas de tres. La lata es un cilindro. Redondea tus respuestas a la centésima más cercana.
Figura\(\PageIndex{15}\)- ¿Cuál es el volumen de una pelota de tenis?
- ¿Cuál es el volumen del cilindro?
- Supongamos que las bolas tocan la lata en los lados, arriba e abajo. ¿Cuál es el volumen del espacio no ocupado por las pelotas de tenis?
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 11.8.
vocabulario
| Término | Definición |
|---|---|
| sólido compuesto | Un sólido que está compuesto, o compuesto por, dos o más sólidos. |
| volumen | Una medición tridimensional que es una medida de cuánto espacio tridimensional ocupa un sólido. |
| Teorema de Pitágoras | El Teorema de Pitágoras es una relación matemática entre los lados de un triángulo rectángulo\(a^{2}+b^{2}=c^{2}\), dada por, donde a y b son patas del triángulo y c es la hipotenusa del triángulo. |
Recursos adicionales
Elemento Interactivo
Video: Principios de sólidos compuestos - Básicos
Actividades: Preguntas de discusión sobre sólidos compuestos
Ayudas de estudio: Guía de estudio de superficie y volumen
Práctica: Sólidos compuestos
Mundo real: Arcos de la naturaleza