9.8: Área y Volumen de Sólidos Similares
- Page ID
- 107251
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Resolver problemas usando relaciones entre sólidos similares.
Comprender las relaciones de escala

Tim tiene un cubo con una longitud lateral de 4 pulgadas. Tiene un cubo similar con dimensiones que son el doble del primer cubo. ¿Cómo se compara el volumen del cubo más grande con el volumen del cubo más pequeño?
En este concepto, aprenderás a entender las relaciones de escala de área y volumen.
Relaciones de escala
Puede comparar las relaciones de escala de distancia, área y volumen al observar figuras tridimensionales. Algunos ejemplos de figuras tridimensionales incluyen un prisma o una pirámide. Al comparar diferentes medidas, verá las relaciones proporcionales entre ellas.
Veamos una situación que involucra volumen.
Brooke tiene un modelo a escala de un almacén. Una unidad de almacenamiento tiene la forma de un prisma rectangular y tiene las dimensiones 4 pulg. por 3 pulg. por 6 in. Si la escala del modelo es\(0.5 \text{ in}=2\text{ ft}\), ¿cuáles son las dimensiones reales de la unidad de almacenamiento? ¿Cuál es el volumen?
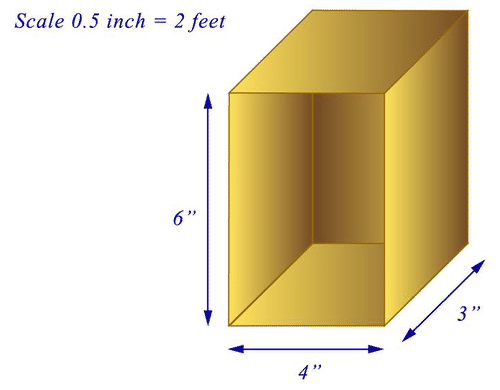
Primero, observe que hay dos partes en este problema. La primera parte es averiguar las dimensiones reales dado que Brooke tiene un modelo a escala. La segunda parte es averiguar el volumen. Comience usando la escala para escribir una proporción para el largo, ancho y alto.
\ (\ begin {aligned}
&\ text {length}\ quad\ text {width}\ quad\ text {altura}\\
&\ frac {0.5\ mathrm {in}} {2\ mathrm {ft}} =\ frac {4\ mathrm {in}} {x\ mathrm {ft}}\ quad\ frac {0.5\ mathrm {in}} {2\ mathrm {ft}} =\ frac {3\ mathrm {in}} {x\ mathrm {ft}}\ quad\ frac {0.5\ mathrm {in}} {2\ mathrm {ft}} =\ frac {6\ mathrm {in}} {x\ mathrm {ft}}
\ end {alineado}\)
A continuación, cruzar multiplicar por cada dimensión.
\ (\ begin {array} {ccc}
\ texto {longitud} &\ texto {ancho} &\ texto {altura}\
\ frac {0.5} {2} =\ frac {4} {x} &\ frac {0.5} {2} =\ frac {3} {x} &\ frac {0.5} {2} =\ frac {6} {x}\\
0.5 x=2\ times 4 & 0.5 x=2\ times 3 & 0.5 x=2\ times 6\\
0.5 x=8 & amp; 0.5 x=6 & 0.5 x=12
\ end {array}\)
Luego, divide ambos lados por 0.5 para resolver para x.
\ (\ begin {array} {ccc}
\ text {length} &\ text {width} &\ text {altura}\\
0.5 x=8 & 0.5 x=6 & 0.5 x=12\
\ frac {0.5 x} {0.5} =\ frac {8} {0.5} &\ frac {0.5 x} {0.5} =\ frac {6} {0.5} &\ frac {0.5 x} {0.5} =\ frac {12} {0.5}\\
x=16 & x=12 & x=24
\ end {array}\)
Las respuestas son 16, 12 y 24.
La longitud de la unidad de almacenamiento es de 16 pies, el ancho es de 12 pies y la altura es de 24 pies.
Entonces, es necesario calcular el volumen de la unidad de almacenamiento.
\(\begin{aligned} V&=l\times w\times h \\ V&=16\times 12\times 24 \\ V&=4608\end{aligned}\)
La respuesta es 4608.
El volumen de la unidad de almacenamiento es\(4608\: ft^{3}\) o 4608 pies cúbicos.
Existe una relación entre el área de la base del prisma y el volumen del prisma. Echemos un vistazo a cómo el área de la base del prisma se relaciona con el volumen del prisma usando el problema de la unidad de almacenamiento.
\(\begin{aligned} A&=l\times w \\ A&=16\times 12 \\ A&=192\end{aligned}\)
El área del prisma es de 192 pies^ {2} o 192 pies cuadrados.
Ahora, para ver la relación entre el volumen de un prisma y el área de un prisma, divida el volumen por el área.
\(\dfrac{V}{A}=4608192\)
\(\dfrac{V}{A}=24\)
La respuesta es 24.
Observe que esta es la altura del prisma.
Ejemplo\(\PageIndex{1}\)
Antes, te dieron un problema sobre los cubos de Tim.
Tim tiene dos cubos donde el más grande es el doble del tamaño que el más pequeño. Esto quiere decir que hay un factor de escala de 2.
Solución
Primero, encuentra las dimensiones del cubo más grande.
El cubo más pequeño tiene una medida lateral de 4 pulgadas. Dado que esto es un cubo, la longitud=anchura = altura=4 pulgadas.
El cubo más grande tendrá una medida lateral de 4 pulg\ times 2=8 in. Por lo tanto la longitud=anchura = altura=8 pulgadas.
A continuación encuentra el volumen de ambos cubos y compara.
\ (\ begin {aligned}
&\ text {Volumen del cubo más pequeño}\ quad\ text {Volumen del cubo más grande}\\
&\ begin {array} {ll}
v=L\ veces w\ veces h & v=L\ veces w\ veces h\
V=4\ mathrm {in}\ times 4\ mathrm {in}\ times 4\ mathrm {in} & V=8\ mathrm {in}}\ tiempos 8\ mathrm {in}\ times 8\ mathrm {in}\\
V=64\ mathrm {in} ^ {3} & V=512\ mathrm {in} ^ {3}
\ end {array}
\ end {alineado}\)
Luego, compara el volumen del cubo más grande con el cubo más pequeño.
\(\begin{aligned} \dfrac{\text{Volume of larger cube}}{\text{Volume of smaller cube}}&=\dfrac{512}{64} \\ \dfrac{\text{Volume of larger cube}}{\text{Volume of smaller cube}}&=8\end{aligned}\)
La respuesta es 8.
El volumen del cubo más grande es 8 veces el volumen del cubo más pequeño.
Ejemplo\(\PageIndex{2}\)
Demostrar que la altura del siguiente prisma se puede encontrar usando una relación de volumen a área para un prisma con una longitud de 6 pulgadas, un ancho de 5 pulgadas y una altura de 9 pulgadas.
Solución
Primero, calcula el volumen del prisma.
\(\begin{aligned} V&=l\times w\times h \\ V&=6\times 5\times 9 \\ V&=270\end{aligned}\)
A continuación, calcule el área del prisma.
\(\begin{aligned} A&=l\times w \\ A&=6\times 5 \\ A&=30 \end{aligned}\)
Después, divida el volumen por el área.
\(\begin{aligned}\dfrac{V}{A}&=\dfrac{270}{30} \\ \dfrac{V}{A}&=9\end{aligned}\)
La respuesta es 9.
Observe que esta es la altura del prisma.
Ejemplo\(\PageIndex{3}\)
Un prisma tiene una longitud de 16 pies, un ancho de 12 pies y una altura de 18 pies. Encuentra el volumen del prisma.
Solución
\(\begin{aligned} V&=l\times w\times h \\ V&=16\times 12\times 18 \\ V&=3456\end{aligned}\)
La respuesta es 3456.
El volumen del prisma es\(3456 ft^{3}\) o 3456 pies cúbicos.
Ejemplo\(\PageIndex{4}\)
Un prisma tiene una longitud de 16 pies, un ancho de 12 pies y una altura de 18 pies. Encuentra el área de la base.
Solución
\(\begin{aligned} A&=l\times w \\ A&=16\times 12 \\ A&=192\end{aligned}\)
La respuesta es 192.
El área del prisma es\(192 ft^{2}\) o 192 pies cuadrados.
Ejemplo\(\PageIndex{5}\)
Escriba una relación comparando el volumen con el área del prisma y simplifique.
Solución
\(\beign{aligned}\dfrac{V}{A}&=\dfrac{3456}{192} \\ \dfrac{V}{A}&=18\end{aligned}\)
La respuesta es 18.
La altura del prisma es de 18 pies.
Revisar
Resuelve cada problema.
1. Un cubo mide 8 pies en cada lado. Un cubo similar tiene dimensiones que son el doble de grandes. ¿Cómo se compara el volumen del cubo más grande con el volumen del cubo más pequeño? Escribe una relación para mostrar la comparación.
2. Un cubo mide 3 pulgadas en cada lado. Un cubo similar tiene dimensiones que son la mitad de las del otro cubo. ¿Cómo se compara el volumen del cubo más grande con el volumen del cubo más pequeño? Escribe una relación para mostrar la comparación
3. Un modelo a escala de una caja de arena tiene dimensiones de 0.5 pulgadas por 3 pulgadas por 4 pulgadas. Si la escala del modelo es de 1 pulgadas=1 pie, ¿cuál es el volumen del sandbox real?
4. Un cubo mide 5 pulgadas en cada lado. Un cubo similar tiene dimensiones que son 3 veces más grandes. ¿Cómo se compara el volumen del cubo más grande con el volumen del cubo más pequeño? Escribe una relación para mostrar la comparación.
5. Una caja de envío mide 16 pulgadas por 12 pulgadas por 8 pulgadas. Una segunda caja tiene un tamaño similar pero cada dimensión es 14 de largo. ¿Cómo se compara el volumen de la segunda caja con el volumen de la primera caja?
6. La pecera de Rina tiene un volumen de 8,000 pulgadas cúbicas. Las dimensiones de la pecera de AVA son todas 12 del tamaño de la de Rina's ¿Cuál es el volumen de la pecera de AVA?
7. Un prisma tiene un ancho de 6 pies, una longitud de 8 pies y una altura de 12 pies. ¿Cuál es el volumen del prisma?
8. ¿Cuál es el área de la base de este prisma?
9. ¿Cuál sería el volumen de un prisma 14 del tamaño del descrito anteriormente?
10. ¿Cuál sería el volumen de un prisma 12 del tamaño del descrito anteriormente?
11. ¿Cuál sería el volumen de un prisma dos veces el tamaño del descrito anteriormente?
12. ¿Qué proporción puedes usar para descubrir la relación entre volumen y área?
13. ¿Qué medida encontrarás cuando simplifiques esta relación?
14. Verdadero o falso. Puede usar la medición a escala para encontrar la altura de un prisma.
15. Verdadero o falso. Puede usar la medición a escala para encontrar las dimensiones de un prisma.
Recursos
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 4.11.
vocabulario
| Término | Definición |
|---|---|
| Área | Área es el espacio dentro del perímetro de una figura bidimensional. |
| Modelo a Escala | Un modelo a escala es un modelo que representa un espacio tridimensional. |
| Tridimensional | Una figura dibujada en tres dimensiones se dibuja utilizando longitud, anchura y altura o profundidad. |
| Bidimensional | Una figura dibujada en dos dimensiones solo se dibuja usando largo y ancho. |
| Volumen | Volumen es la cantidad de espacio dentro de los límites de un objeto tridimensional. |
Video: Principios de Sólidos Similares - Básicos
Actividades: Área y Volumen de Sólidos Similares Preguntas de Discusión
Ayudas de estudio: Guía de estudio de superficie y volumen
Práctica: Área y Volumen de Sólidos Similares
Mundo real: ¿Hay vida ahí fuera?

