9.9: Aplicaciones de área superficial y volumen
- Page ID
- 107313
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Utilice sólidos geométricos para modelar objetos del mundo real y resolver problemas. Encuentra densidad por la proporción de masa, personas o cosas con respecto al volumen o área.
Modelado en tres dimensiones
Mark quiere hacer una caja abierta a partir de un trozo de papel de 8.5 pulgadas por 11 pulgadas cortando cuadrados de cada esquina, doblando los lados y asegurándolo con cinta adhesiva. ¿Cómo se relaciona el volumen de su caja con el tamaño de los cuadrados que recorta?
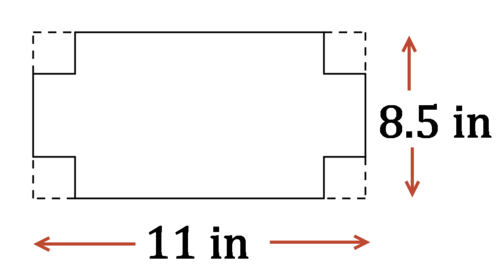
Modelado en tres dimensiones
Vives en un mundo tridimensional. Mira a tu alrededor y observa lo que ves a lo largo de tu día. ¿Puedes encontrar ejemplos de prismas? ¿Cilindros? ¿Pirámides? ¿Conos? ¿Esferas?
Si bien la mayoría de los objetos en tu vida diaria no son perfectos prismas, pirámides, cilindros, conos o esferas, la mayoría están cerca de uno de estos cinco sólidos o una combinación de estos sólidos. Modelar en tres dimensiones se trata de poder elegir el mejor sólido para ayudar a analizar una situación tridimensional del mundo real, y luego usar tus conocimientos de geometría para tomar decisiones sobre la situación de la vida real. Deberías preguntarte:
- ¿Qué sólidos o sólidos son el mejor modelo de este objeto de la vida real?
- ¿Qué problemas estoy tratando de resolver o decisiones estoy tratando de tomar sobre el objeto de la vida real?
- ¿Qué información sobre el objeto de la vida real me dan y dónde encaja en mi modelo?
Aplicación en el mundo real: cortar árboles
Una gran tormenta hace que un árbol grande caiga en tu patio. La porción principal del tronco del árbol mide aproximadamente 9 pies alrededor y mide 40 pies de largo. Planeas cortar el árbol para usar y vender como leña de fuego. Aproximadamente, ¿qué volumen de madera obtendrás del árbol?
El tronco de un árbol se modela mejor con un cilindro. Aquí, está buscando el volumen aproximado del cilindro. Se dan dos piezas de información.
1. “La porción principal del tronco del árbol mide aproximadamente 9 pies alrededor” — Esta es la circunferencia de la base del cilindro. Puede utilizar esta medida para encontrar el radio del cilindro.
\(2\pi r=9\rightarrow r=\dfrac{9}{2\pi} \rightarrow r\approx 1.43\text{ ft}\)
2. “40 pies de largo” — Esta es la altura del cilindro.
\(h=40\text{ ft}\)
El volumen de la madera del árbol es aproximadamente:
\(V=\pi r^{2}h=\pi (1.43^{2})(40)\approx 257\text{ ft}^{3}\)
Aplicación en el mundo real: compra de madera
La madera se vende comúnmente en cordones. Un cordón de madera es una pila de madera apretada que mide 4 pies por 4 pies por 8 pies. Aproximadamente, ¿cuántas cuerdas de madera producirá el árbol picado del primer problema?
Un cordón de madera se modela mejor con un prisma rectangular. \(V=A_{Base}\cdot h\), entonces\(V=(4\cdot 4)\cdot 8=128 ft^{3}\). Cada cordón de madera tiene aproximadamente 128 pies cúbicos de madera. Dado que el árbol del primer problema produjo 257 pies cúbicos de madera, se trata de\(\dfrac{257}{128}\approx 2\) cordones de madera.
Ahora, vamos a llegar a una ecuación que relacione la longitud alrededor de un árbol en pies, la altura de un árbol en pies, y el número aproximado de cuerdas de madera que producirá un árbol.
Se quiere llegar a una ecuación que tome una entrada de circunferencia y altura y produzca una salida de cordones de madera. Piense en los pasos dados en los Ejemplos A y B y repita estos pasos con variables para circunferencia y altura en lugar de valores específicos.
- Let\(C= \text{ distance around the tree}\)
- Let\(h= \text{ height of tree}\)
Usa la distancia alrededor del árbol para encontrar el radio:
\(C=2\pi r\rightarrow r=C^2\pi\)
El volumen de la madera del árbol es:
\(\begin{aligned} V&=\pi r^{2}h \\ &=\pi (\dfrac{C}{2\pi})^{2}h \\ &=\dfrac{C^{2}h}{4\pi}\end{aligned}\)
Una vez que se tiene el volumen de la madera de un árbol dado, para encontrar el número de cuerdas de madera se divide el volumen por 128 ft3, que es el número de pies cúbicos en un cordón de madera.
\(\text{Number of Cords}=\dfrac{V}{128}=\dfrac{\dfrac{C^{2}h}{4\pi }}{128}=\dfrac{C^{2}h}{512\pi}\)
Prueba esta fórmula usando la información original del primer problema sobre cortar árboles para ver si obtienes la respuesta correcta al segundo problema. En este primer problema, C=9 pies y h=40 ft.
\(\text{Number of Cords}=\dfrac{C^{2}h}{512\pi }=\dfrac{(9^{2})(40)}{512\pi }\approx 2.01\)
Esto coincide con la respuesta a, para que puedas estar seguro de que tu ecuación es correcta.
Ejemplo\(\PageIndex{1}\)
Anteriormente, se le preguntó cómo se relaciona el volumen de la caja de Mark con el tamaño de los cuadrados que recortó.
Solución
Deje que el largo del lado del cuadrado que Mark recorta de cada esquina sea x La porción del papel que se convertirá en la base de la caja una vez que esté hecha está sombreada abajo en rojo.
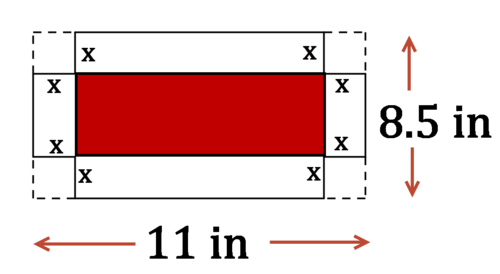
La caja es un prisma rectangular. El volumen de la caja es por lo tanto\ (V=A_ {Base}\ cdot h.
- \(A_{Base}=(11−2x)(8.5−2x)=4x^{2}−39x+93.5\)
- \(h=x\)
Por lo tanto, el volumen de la caja en cuanto al tamaño del cuadrado es:
\(V=x(4x2−39x+93.5)=4x^{3}−39x^{2}+93.5x.\)
Mark puede usar esta fórmula para determinar el volumen de la caja dada la longitud del lado de los cuadrados que corta. Por ejemplo, si corta cuadrados que son de 2 pulgadas por 2 pulgadas, entonces x=2. El volumen de la caja sería:
\(V=4(2^{3})−39(2^{2})+93.5(2)=63 in^{3}\)
Ejemplo\(\PageIndex{2}\)
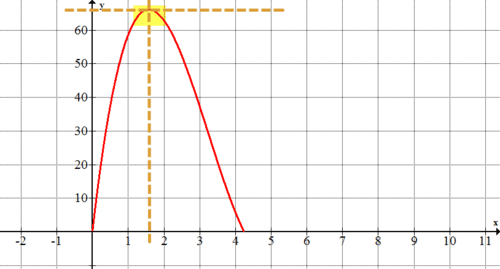
Grafica la ecuación\(y=4x^{3}−39x^{2}+93.5x\) con una calculadora gráfica. ¿Qué representan los puntos de esta gráfica? ¿Qué parte de esta gráfica es relevante para este problema?
Solución
Los puntos en la gráfica representan el volumen de la caja dada la longitud del lado de cada cuadrado recortado.
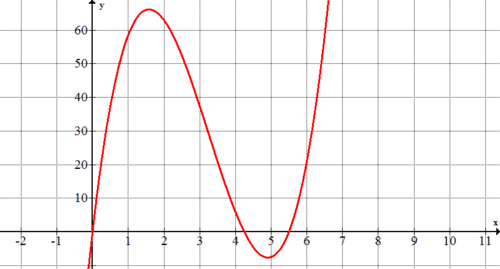
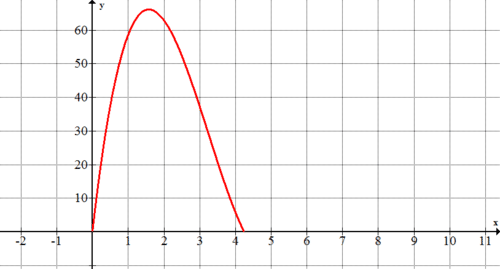
Debido a que Mark no puede cortar un cuadrado con una longitud lateral negativa o un cuadrado con una longitud lateral mayor a 4.25 pulgadas (porque el papel tiene solo 8.5 pulgadas de ancho), la porción de la gráfica que es relevante es la porción con\(x\) valores entre 0 y 4.25.
Ejemplo\(\PageIndex{3}\)
Aproximadamente, ¿qué tamaño cuadrados maximizarán el volumen de la caja (harán que la caja tenga el mayor volumen posible)? ¿Cómo te ayuda la gráfica de #1 a responder a esta pregunta?
Solución
El volumen máximo parece ocurrir con cuadrados que son aproximadamente 1.6 pulgadas por 1.6 pulgadas. El volumen en ese punto parece estar alrededor\(66 in^{3}\). El gráfico ayuda a responder a esta pregunta porque el pico en la gráfica es donde se produce el volumen máximo.
Ejemplo\(\PageIndex{4}\)
¿El tamaño del cuadrado que maximiza el volumen también maximiza el área de superficie de la caja? Explique.
Solución
El área de superficie de la caja abierta será el área de la caja desplegada (la red). Cuanto más corte del papel, menor será el área de superficie. Por lo tanto, el tamaño del cuadrado que maximiza el volumen tampoco maximiza el área de superficie de la caja.
Revisar
Un rollo de toallas de papel de 11 pulgadas de alto tiene un tubo interno de cartón con un diámetro de 1.5 pulgadas. El ancho de la toalla de papel en el rollo es de 2 pulgadas y cada toalla de papel tiene un grosor de 0.015 pulgadas.
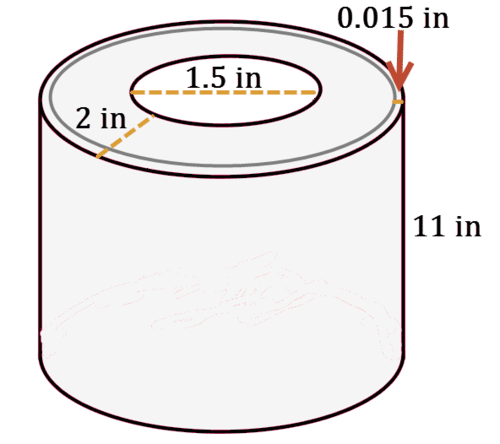
1. ¿Cuál es el volumen de las toallas de papel? ¿Cambiará el volumen si se desenrolla el rollo de toallas de papel?
2. Si se desenrolla todo el rollo de toallas de papel, ¿cuánto tiempo durará la cadena de toallas de papel desenrolladas? [Pista: Usa tu respuesta a #1 para ayudar]
3. Crea una ecuación que generalice la relación entre las variables: diámetro del tubo, ancho de toalla de papel en rollo, grosor de toalla de papel y longitud de toallas de papel desenrolladas. ¿Por qué la altura del rollo de toallas de papel no importa en esta relación?
Para decorar un pastel con glaseado morado, Sam planea llenar una bolsa sándwich con cremallera con glaseado, cortar una de las puntas de la bolsa y exprimir el glaseado de la esquina (ver imagen abajo).
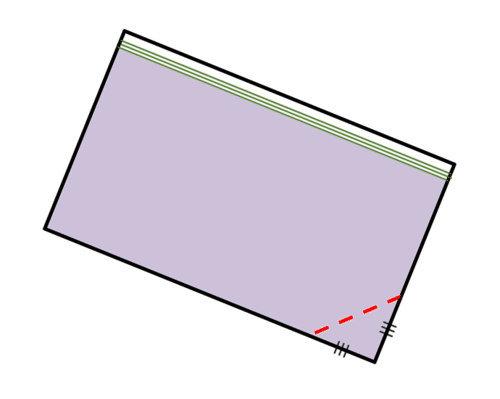
4. Suponiendo que corta un triángulo isósceles de la esquina, qué longitud de corte debe hacer para glaseado de tubería con un diámetro de 1 centímetro. En otras palabras, ¿cuál debería ser la longitud de la línea punteada roja?
5. Dar una ecuación que muestre la relación entre la longitud del corte realizado y el diámetro del glaseado a medida que sale de la bolsa.
6. Estás empacando anuarios que miden 11 pulgadas por 14 pulgadas por 1.5 pulgadas. Tienes cajas que miden 12 pulgadas por 30 pulgadas por 10 pulgadas. ¿Cuántos libros caben en cada caja?
Una cierta vela encendida pierde\ (7 in^ {3} de volumen cada hora.

7. Si la vela original medía 10 pulgadas de alto con un diámetro de 3 pulgadas, ¿cuál es el volumen de la vela después de 3 horas?
8. Crear una ecuación que relacione la altura original de la vela, el diámetro de la vela, el tiempo quemado y el volumen actual de la vela para todas las velas que pierden\(7 in^{3}\) de volumen por hora.
9. Mike y sus amigos están teniendo una pelea de globos de agua. Cada globo aproximadamente esférico puede contener una taza de agua. Si una taza de agua tiene un volumen de aproximadamente\(14.44 in^{3}\), ¿cuál es el radio de cada globo lleno?
Marissa trabaja en una heladería. Los conos de azúcar tienen un diámetro de 2 pulgadas y una altura de 4 pulgadas. Para un cono de una sola cucharada, empaca el cono con helado y luego pone una cucharada encima. Para un cono de doble cucharada, empaca el cono con helado y luego pone dos bolas encima (ver boceto a continuación). Para un cono de triple cucharada, empaca el cono con helado y luego pone tres bolas encima. Una taza de helado tiene un volumen de\(14.44 in^{3}\).

10. Aproximadamente ¿cuánto helado (en tazas) obtiene un cono de una sola cucharada?
11. Aproximadamente ¿cuánto helado (en tazas) obtiene un cono de doble cucharada?
12. Aproximadamente ¿cuánto helado (en tazas) obtiene un cono de triple cucharada?
13. Describe al menos dos razones por las que tus respuestas a las tres preguntas anteriores son sólo aproximadas.
14. Si un cono de cuchara simple cuesta $2.50 y un cono de cuchara doble cuesta $3.50. ¿Qué tipo de cono es mejor teniendo en cuenta el costo por taza de helado?
15. Si un cono de pala simple cuesta $2.50, ¿cuánto debería costar un cono de triple pala si tiene un precio justo?
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 9.5.
El vocabulario
| Término | Definición |
|---|---|
| Circunferencia | La circunferencia de un círculo es la medida de la distancia alrededor del borde exterior de un círculo. |
Recursos adicionales
Práctica: Aplicaciones de área superficial y volumen

