9.10: Superficie y Volumen de Prismas
- Page ID
- 107292
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Figuras 3-D con 2 bases congruentes en planos paralelos y rectángulos para sus otras caras.
Prismas
Un prisma es una figura tridimensional con 2 bases congruentes, en planos paralelos, en los que las otras caras son rectángulos.
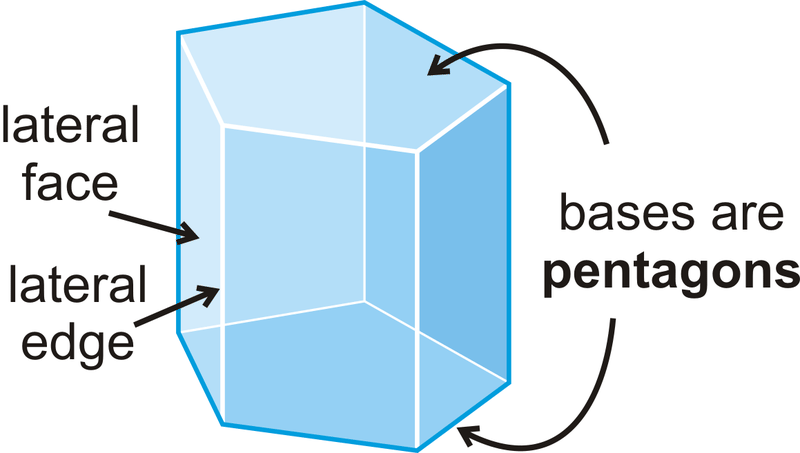
Las caras no base son caras laterales . Los bordes entre las caras laterales son bordes laterales .
Este ejemplo particular es un prisma pentagonal porque su base es un pentágono. Los prismas son nombrados por la forma de su base. Los prismas se clasifican como prismas derechos (prismas donde todas las caras laterales son perpendiculares a las bases) o prismas oblicuos (prismas que se inclinan hacia un lado, cuya base es un paralelogramo más que un rectángulo, y cuya altura es perpendicular al plano de la base), como se muestra a continuación.
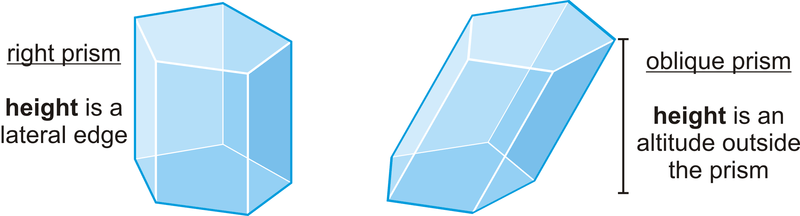
Superficie
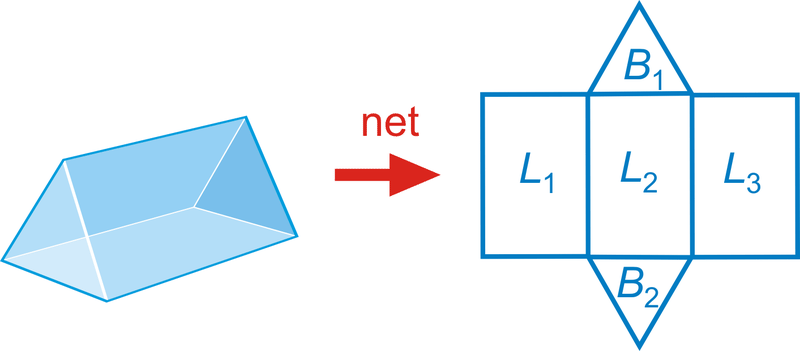
Para encontrar el área superficial de un prisma, busque la suma de las áreas de sus caras. El área lateral es la suma de las áreas de las caras laterales. La unidad básica de área es la unidad cuadrada.
\(Surface Area=B_{1}+B_{2}+L_{1}+L_{2}+L_{3}\)
\(Lateral Area=L_{1}+L_{2}+L_{3}\)
Volumen
Para encontrar el volumen de cualquier sólido debes averiguar cuánto espacio ocupa. La unidad básica de volumen es la unidad cúbica.
Para los prismas en particular, para encontrar el volumen se debe encontrar el área de la base y multiplicarla por la altura.
Volumen de un prisma:\(V=B\cdot h\), dónde\(B= area\: of\: base\).

Si un prisma oblicuo y un prisma derecho tienen la misma área base y altura, entonces tendrán el mismo volumen. Esto se debe al Principio de Cavalieri, que establece que si dos sólidos tienen la misma altura y la misma área de sección transversal en cada nivel, entonces tendrán el mismo volumen.
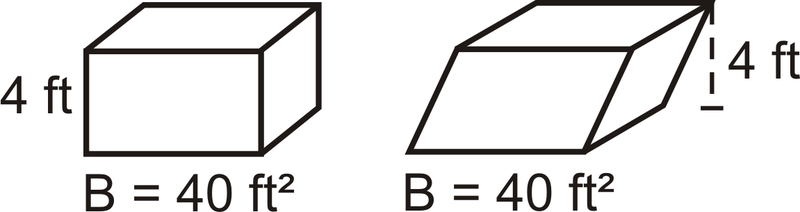
¿Y si te dieran una figura tridimensional sólida con dos bases congruentes en las que las otras caras fueran rectángulos? ¿Cómo podrías determinar cuánto espacio bidimensional y tridimensional ocupa esa figura?
Ejemplo\(\PageIndex{1}\)
La superficie total del prisma triangular es\(540\text{ units}^{2}\). ¿Qué es\(x\)?
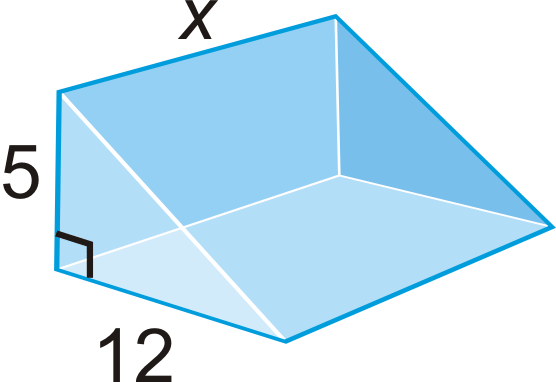
Solución
La superficie total es igual a:
\(A_{2\: triangles}+A_{3\: rectangles}=540\)
La hipotenusa de las bases triangulares es 13,\(5^{2}+12^{2}\). Vamos a rellenar lo que sabemos.

\(\begin{aligned} A_{2\: triangles}=2(\dfrac{1}{2}\cdot 5\cdot 12)=60 \\ A_{3\: rectangles}&=5x+12x+13x=30x \\ 60+30x &=540 \\ 30x&=480 \\ x&=16\text{ units }\qquad \text{ The height is 16 units.}\end{aligned}\)
Ejemplo\(\PageIndex{2}\)
Encuentra el volumen del prisma rectangular derecho a continuación.
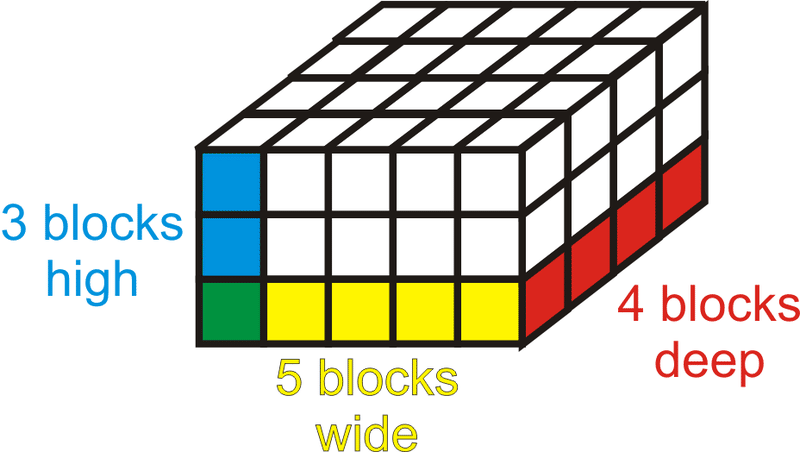
Solución
El área de la base es\((5)(4)=20\) y la altura es 3. Entonces el volumen total es\((20)(3)=60\text{ unit}^{3}\)
Ejemplo\(\PageIndex{3}\)
Encuentra el área de superficie del prisma a continuación.
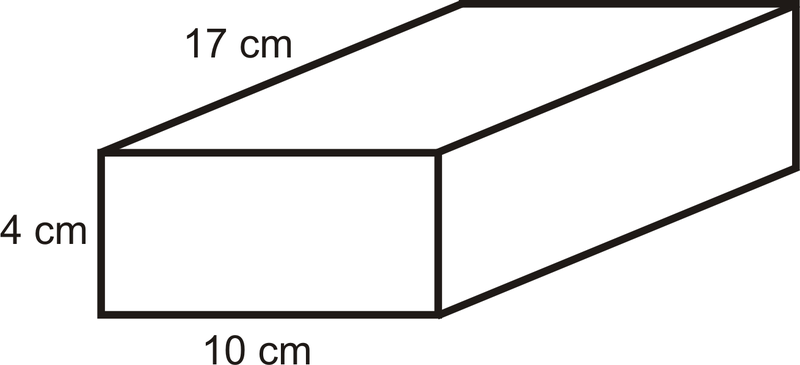
Solución
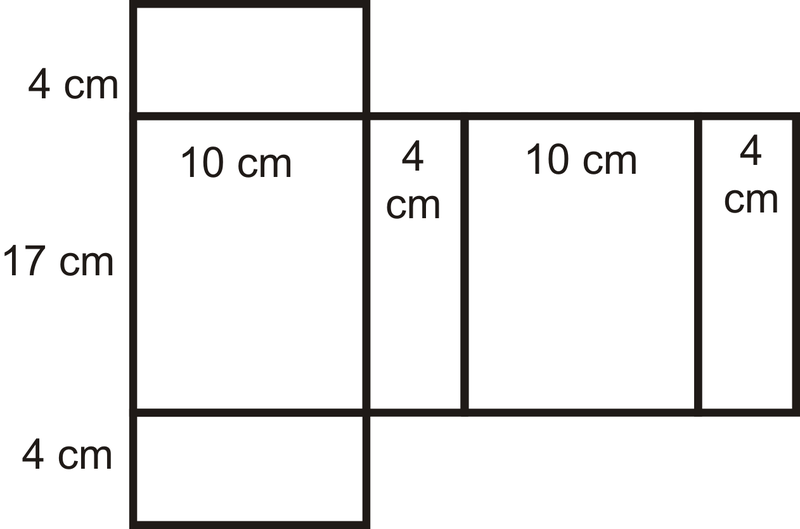
Para resolver, dibuja la red del prisma para que podamos asegurarnos de encontrar el área de TODAS las caras.
Usando la red, tenemos:
\(\begin{aligned} SA_{prism}&=2(4)(10)+2(10)(17)+2(17)(4)\\ &=80+340+136 \\ &=556 \text{ cm}^{2}\end{aligned}\)
Ejemplo\(\PageIndex{4}\)
Encuentra el área de superficie del prisma a continuación.
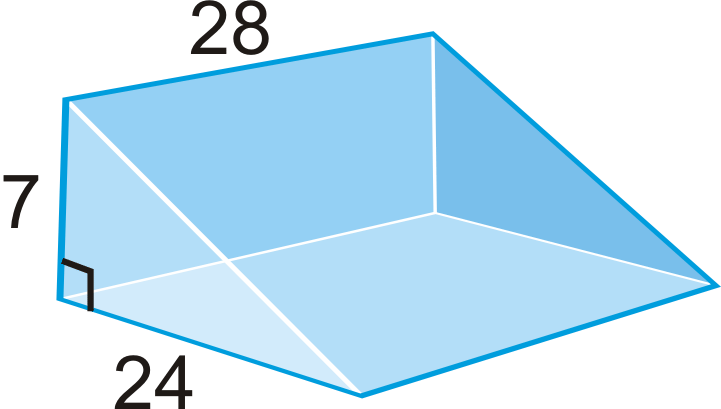
Solución
Se trata de un prisma triangular derecho. Para encontrar la superficie, necesitamos encontrar la longitud de la hipotenusa de la base porque es el ancho de una de las caras laterales. Podemos usar el Teorema de Pitágoras para encontrar esta longitud.
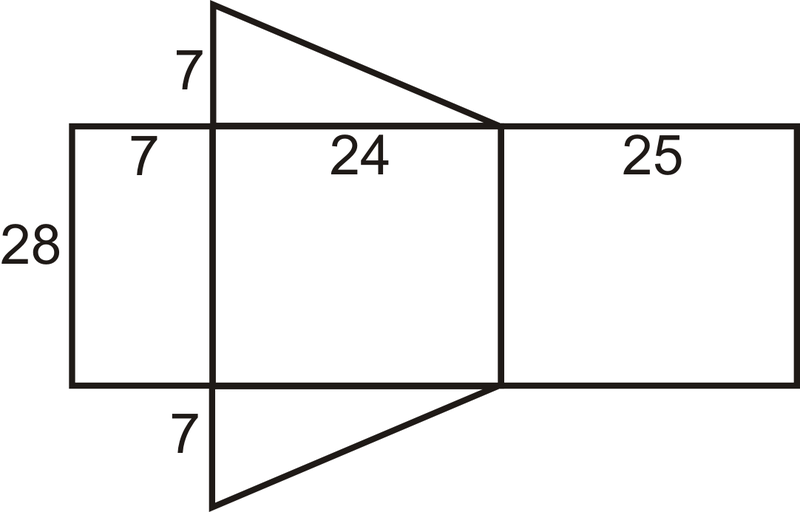
\(\begin{aligned} 7^{2}+24^{2}&=c^{2} \\ 49+576&=c^{2} \\ 625&=c^{2} \qquad c=25\end{aligned}\)
Mirando a la red, la superficie es:
\(\begin{aligned} SA&=28(7)+28(24)+28(25)+2(\dfrac{1}{2}\cdot 7\cdot 24) \\ SA&=196+672+700+168=1736 units^{2}\end{aligned}\)
Ejemplo\(\PageIndex{5}\)
Tienes una pequeña tienda triangular en forma de prisma. ¿Cuánto volumen tiene una vez que está configurado?
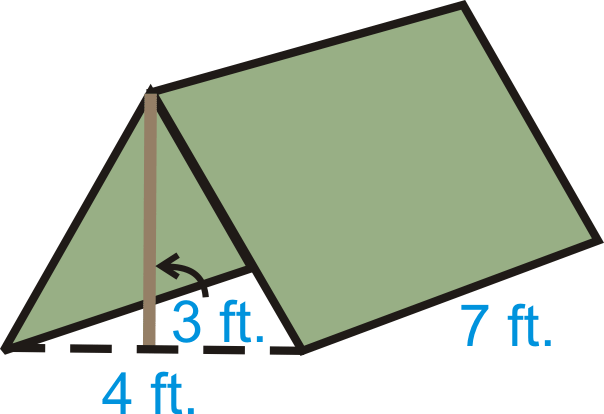
Solución
Primero, necesitamos encontrar el área de la base.
\(\begin{aligned} B&=\dfrac{1}{2}(3)(4)=6 \text{ ft}^{2} \\ V&=Bh=6(7)=42 \text{ ft}^{3}\end{aligned}\)
A pesar de que la altura en este problema no parece una “altura”, es porque es el segmento perpendicular que conecta las dos bases.
Revisar
- ¿Qué tipo de prisma es este?
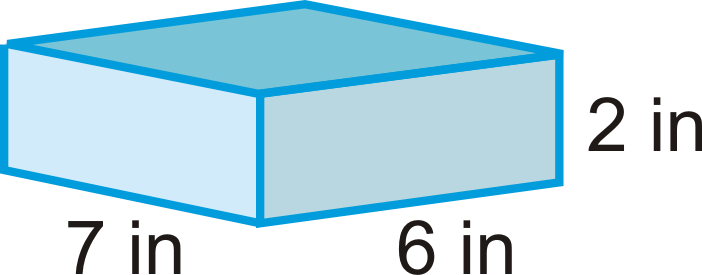
Figura\(\PageIndex{14}\) - Dibuja la red de este prisma.
- Encuentra el área de las bases.
- Encuentra el área de caras laterales, o el área de superficie lateral.
- Encuentra la superficie total del prisma.
- ¿Cuántos cubos de una pulgada pueden caber en una caja que mide 8 pulgadas de ancho, 10 pulgadas de largo y 12 pulgadas de alto? ¿Esto es lo mismo que el volumen de la caja?
- Una caja de cereales en 2 pulgadas de ancho, 10 pulgadas de largo y 14 pulgadas de alto. ¿Cuánto cereal contiene la caja?
- Una lata de refresco mide 4 pulgadas de alto y tiene un diámetro de 2 pulgadas. ¿Cuánto refresco contiene la lata? Redondea tu respuesta a la centésima más cercana.
- Un cubo sostiene\(216\text{ in}^{3}\). ¿Cuál es la longitud de cada borde?
- Un cubo tiene lados que son de 8 pulgadas. ¿Cuál es el volumen?
Utilice el prisma triangular derecho para responder a las preguntas 11-15.
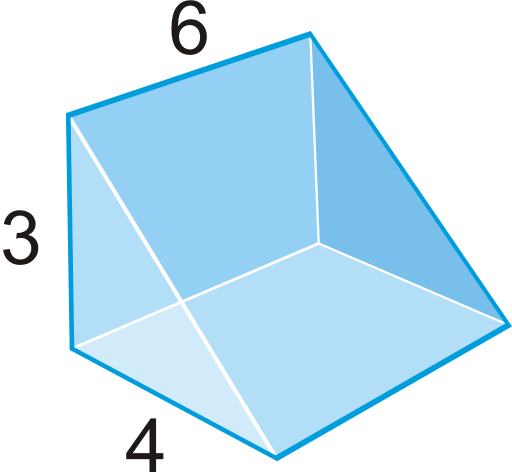
- Encuentra el volumen del prisma.
- ¿Qué forma son las bases de este prisma? ¿Cuáles son sus áreas?
- ¿Cuáles son las dimensiones de cada una de las caras laterales? ¿Cuáles son sus áreas?
- Encuentra el área de superficie lateral del prisma.
- Encuentra la superficie total del prisma.
- Describir la diferencia entre el área de superficie lateral y la superficie total.
- Los dados difusos son cubos con lados de 4 pulgadas.

Figura\(\PageIndex{16}\) - ¿Cuál es el volumen y la superficie de una matriz?
- ¿Cuál es el volumen y la superficie de ambos dados?
Encuentra el volumen de los siguientes sólidos. Redondea tus respuestas a la centésima más cercana.
- las bases son trapezoides isósceles
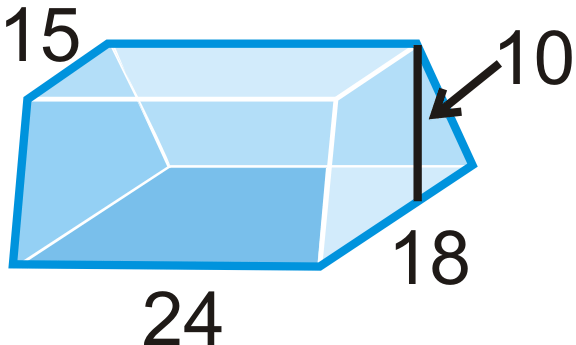
Figura\(\PageIndex{17}\) -
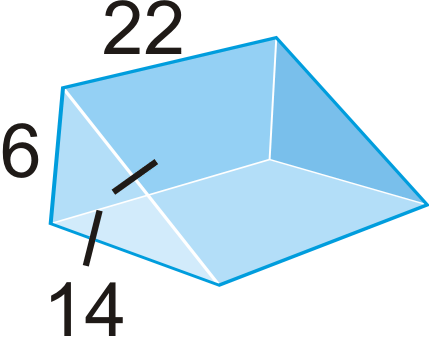
Figura\(\PageIndex{18}\) -
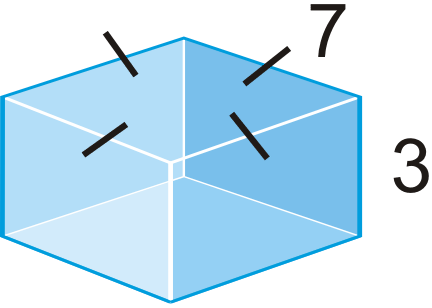
Figura\(\PageIndex{19}\) -
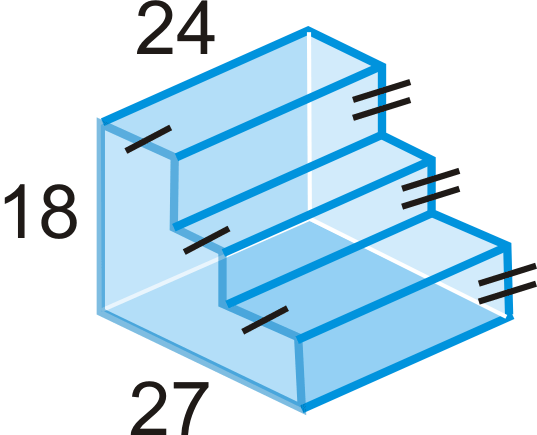
Figura\(\PageIndex{20}\)
Encontrar el valor de\(x\), dada la superficie.
- \(V=504 \text{ unit}^{3} \)
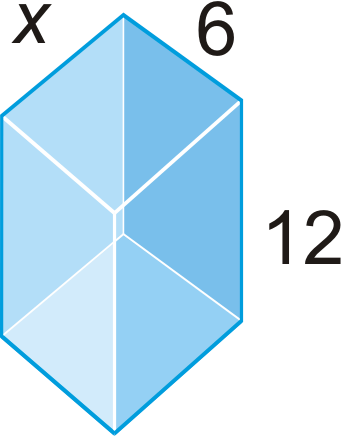
Figura\(\PageIndex{21}\) - \(V=2688\text{ unit}^{3} \)
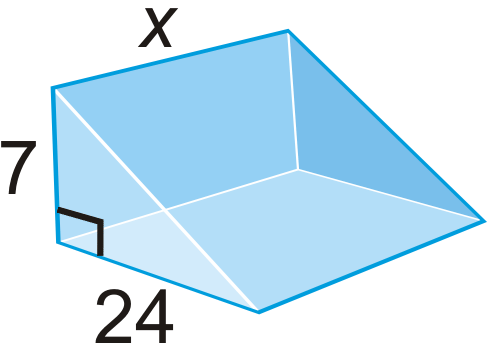
Figura\(\PageIndex{22}\)
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 11.3.
vocabulario
| Término | Definición |
|---|---|
| bordes laterales | Bordes entre las caras laterales de un prisma. |
| prisma oblicuo | Un prisma que se inclina hacia un lado y cuya altura es perpendicular al plano de la base. |
| prisma | es una figura tridimensional con 2 bases congruentes, en planos paralelos, y en la que las otras caras son rectángulos. |
| prisma derecho | Un prisma donde todas las caras laterales son perpendiculares a las bases. |
| Superficie | El área superficial es el área total de todas las superficies de un objeto tridimensional. |
| Volumen | El volumen es la cantidad de espacio dentro de los límites de un objeto tridimensional. |
| Caras Laterales | Todas las caras de un prisma aparte de la base se conocen como caras laterales. |
Recursos adicionales
Elemento Interactivo
Video: Principios de prismas - Básicos
Actividades: Prismas Preguntas de Discusión
Ayudas de estudio: Guía de estudio de prismas y cilindros
Práctica: Superficie y Volumen del Prisma

