9.11: Superficie de prismas
- Page ID
- 107338
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Utilice fórmulas para encontrar el área de superficie de prismas rectangulares y prismas triangulares.
Superficie de prismas triangulares

Max compró un prisma de luz para su mamá para el Día de la Madre. Quiere averiguar cuánto papel de envolver se necesita para envolverlo. Para ello, necesita averiguar la superficie del regalo. El extremo triangular tiene una base de 3 cm y una altura de 4 cm. La longitud de cada lado es de 6 cm y la altura del prisma (longitud del lado rectangular) es de 8 cm. ¿Cuál es la superficie del regalo que Max compró para su mamá?
En este concepto, aprenderás a calcular el área superficial de un prisma triangular.
Encontrar el área de superficie de un prisma triangular
Área es el espacio que está contenido en una figura bidimensional. El área superficial es el área total de todos los lados y caras de una figura tridimensional. Para encontrar el área de superficie, se calcula el área de cada cara y luego se suman estas áreas juntas.
Una forma de hacerlo es usar una red, ya que una red es una representación bidimensional de un sólido tridimensional, o una imagen desplegada de un sólido.
¿Cuál es la superficie de la figura a continuación?

La red para este prisma triangular es la siguiente:
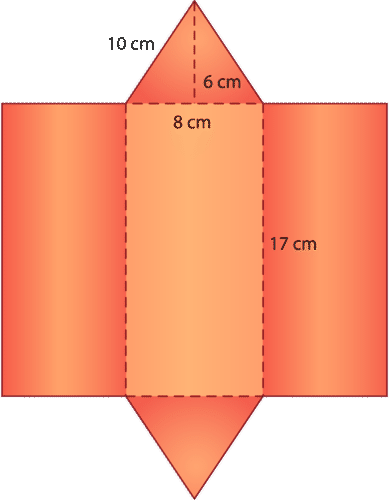
Ahora, vamos a rellenar las medidas para los lados de cada cara con el fin de calcular su área. Los prismas triangulares tienen su propia fórmula para encontrar área de superficie porque tienen dos caras triangulares opuestas entre sí.
La fórmula\( A=\dfrac{1}{2}bh\) se utiliza para encontrar el área de las caras triangulares superiores y bases, donde A = área, b = base y h = altura. La fórmula\(A=lw\) se utiliza para encontrar el área de las tres caras laterales rectangulares, donde A = área, l = longitud y w = ancho.
Tapando las medidas que se dan en la red, calcule el área de cada cara. Recuerda usar la fórmula de área correcta para los triángulos y rectángulos.
\ (\ begin {array} {llllll}
\ texto {Cara inferior} &\ texto {Cara superior} &\ texto {lado} &\ texto {lado} &\ texto {lado} &\ texto {lado}\\
A=\ frac {1} {2} b h y A=\ frac {1} {2} b h & a=L w & a=L w y a=L w
\\ frac {1} {2} (8) (6) + &\ frac {1} {2} (8) (6) + & 17\ times 10+ & 17\ times 10+ & 17\ times 8\\
24 & + & 24 & + & amp; 170 & + & 170 & + & 136\\
=524\ mathrm {~cm} ^ {2} & & & & &
\ end {array}\)
Al sumar estos valores juntos, se obtiene una superficie de 524 centímetros cuadrados para este prisma triangular.
\(SA=bh+(s_{1}+s_{2}+s_{3})H\)
También puede usar una fórmula para calcular el área de superficie de un prisma triangular que puede ahorrar tiempo durante el proceso de usar una red para derivar las áreas:
donde b = base; h = altura del triángulo; s_ {1}\), s_ {2}\), y s_ {3}\) = la longitud de cada lado de la base del triángulo, y H = la altura del prisma (que es la longitud de los rectángulos).
Primero, encuentra el área de las dos caras triangulares. Cada cara tendrá un área de 12bh. Recuerda, puedes usar una fórmula para calcular el área de un par de caras. Por lo tanto, puede duplicar esta fórmula para encontrar el área de ambas caras triangulares a la vez lo que resulta en la fórmula 2 (12bh). El 2 multiplicado por el 12 equivale a 1, o se cancela entre sí, y te quedas con bh.
A continuación, es necesario calcular el área de cada una de las caras laterales rectangulares. La longitud de cada rectángulo es la misma que la altura del prisma, así llama a esto H. El ancho de cada rectángulo es en realidad el mismo que los lados de la base triangular. En lugar de multiplicar la longitud y el ancho para cada rectángulo, puedes combinar esta información. Dado que hay 3 anchuras rectangulares (todas iguales a los lados de los triángulos), multiplique el perímetro de la base triangular por la altura de los rectángulos, H, que dará el área de los tres rectángulos.
Si juntas estas piezas, el área de las bases y el área de las caras laterales, obtienes esta fórmula:
\(SA=bh+(s_{1}+s_{2}+s_{3})H\)
donde bh = el área de la parte superior y base del triángulo, y (\(s_{1}+s_{2}+s_{3})H\)= el área de las caras laterales rectangulares.
Recuerde que la altura de la base triangular (\(h\)) no es necesariamente la misma que la altura del prisma (H).
Ejemplo\(\PageIndex{1}\)
Antes, te dieron un problema sobre el regalo que Max compró para su mamá.
El extremo triangular tiene una base de 3 cm y una altura de 4 cm. La longitud de cada lado es de 6 cm y la altura del prisma (longitud del rectángulo) es de 8 cm. ¿Cuál es la superficie de este prisma triangular?
Solución
Primero, sustituya los valores dados en la fórmula.
\(\begin{aligned} SA&=bh+(s_{1}+s_{2}+s_{3})H \\ SA&=3(4)+(3+6+6)(8)\end{aligned}\)
A continuación, multiplique los tiempos base altura para el área de los triángulos (bh), y agregue sus tres lados (\(s_{1} + s_{2} + s_{3}\)).
\(SA=12+15(8)\)
Luego, multiplica la suma de los lados del triángulo por la altura del prisma (H\)) y suma los valores juntos para la respuesta, recordando incluir la unidad de medida apropiada.
\(\begin{aligned} SA&=12+120 \\ SA&=132\text{ cm}^{2}\end{aligned}\)
La respuesta es que la superficie del regalo que Max compró para su mamá es de 132 centímetros cuadrados.
Ejemplo\(\PageIndex{1}\)
Calcule el área de superficie del siguiente prisma triangular:
Solución
Primero, sustituya los valores dados en la fórmula.
\(\begin{aligned} SA&=bh+(s_{1}+s_{2}+s_{3})H \\ SA&=4(6)+(4+7+7)(12)\end{aligned}\)
A continuación, multiplique los tiempos base altura para el área de los triángulos (bh) y agregue los tres lados del triángulo (\(s_{1} + s_{2} + s_{3}\)).
\(SA=24+18(12)\)
Luego, multiplica la suma de los lados del triángulo por la altura del prisma (H) y suma los valores juntos para la respuesta, asegurándose de incluir la unidad de medida apropiada.
\(\begin{aligned} SA&=24+216 \\ SA&=240 cm^{2}\end{aligned}\)
La respuesta es que la superficie del prisma triangular anterior es de 240 centímetros cuadrados.
Ejemplo\(\PageIndex{1}\)
Un prisma triangular tiene un extremo triangular con una base de 5 pulgadas y una altura de 4 pulgadas. La longitud de cada lado es de 8 pulgadas y el ancho de cada lado es de 6 pulgadas. ¿Cuál es la superficie del prisma?
Solución
Primero, sustituya los valores dados en la fórmula.
\(\begin{aligned} SA&=bh+(s_{1}+s_{2}+s_{3})H \\ SA&=5(4)+(5+6+6)(8)\end{aligned}\)
A continuación, multiplique los tiempos base altura para el área de los triángulos (bh), y agregue sus tres lados (s_ {1} + s_ {2} + s_ {3}\)).
\(SA=20+17(8)\)
Después, multiplica la suma de los lados del triángulo por la altura del prisma (H) y suma los valores juntos para la respuesta, recordando incluir la unidad de medida apropiada.
\(\begin{aligned} SA&=20+136 \\ SA&=156\text{ in}^{2}\end{aligned}\)
La respuesta es que la superficie del prisma triangular anterior es de 156 pulgadas cuadradas.
Ejemplo\(\PageIndex{1}\)
Un prisma triangular tiene un extremo triangular con una base de 8 pies y una altura de 6 pies. La longitud de cada lado es de 10 pies y el ancho de cada lado es de 6 pies. ¿Cuál es la superficie del prisma?
Solución
Primero, sustituya los valores dados en la fórmula.
\(\begin{aligned} SA&=bh+(s_{1}+s_{2}+s_{3})H \\ SA&=8(6)+(8+6+6)(10)\end{aligned}\)
A continuación, múltiples los tiempos base altura para el área de los triángulos (bh), y añadir los tres lados del triángulo (s_ {1} + s_ {2} + s_ {3}\)).
\(SA=48+20(10)\)
Luego, multiplica la suma de los lados del triángulo por la altura del prisma (H) y suma los valores juntos para la respuesta, asegurándose de incluir la unidad de medida apropiada.
\(\begin{aligned} SA&=48+200 \\ SA&=248\text{ ft}^{2}\end{aligned}\)
La respuesta es que la superficie del prisma triangular anterior es de 248 pies cuadrados.
Ejemplo\(\PageIndex{1}\)
Un prisma triangular tiene un extremo triangular con una base de 12 pulgadas y una altura de 9 pulgadas. La longitud de cada lado es de 14 pulgadas y el ancho de cada lado es de 9 pulgadas. ¿Cuál es la superficie del prisma?
Solución
Primero, sustituya los valores dados en la fórmula.
\(\begin{aligned} SA&=bh+(s_{1}+s_{2}+s_{3})H \\ SA&=12(9)+(9+9+9)(14)\end{aligned}\)
A continuación, multiplique los tiempos base altura para el área de los triángulos (bh\)), y agregue los tres lados del triángulo (\(s_{1} + s_{2} + s_{3}\)).
\(SA=108+27(14)\)
Luego, multiplica la suma de los lados del triángulo por la altura del prisma (H\)) y suma los valores juntos para la respuesta, asegurándose de incluir la unidad de medida apropiada.
\(\begin{aligned} SA&=108+378 \\ SA&=486\text{ in}^{2}\end{aligned}\)
La respuesta es que la superficie del prisma triangular anterior es de 486 pulgadas cuadradas.
Revisar
Utilice la siguiente figura para responder a cada pregunta.

- ¿Qué unidad son las medidas de esta cifra?
- ¿Cuál es la longitud de la base?
- ¿Cuál es el ancho de la base?
- ¿Cuál es la forma de los lados?
- ¿Cuál es la medida del lado triangular?
- ¿Cuál es la fórmula para encontrar el área superficial de un prisma triangular?
- ¿Cuál es la superficie de esta figura?
Encuentra el área de superficie de cada prisma triangular.
- Un prisma triangular tiene un extremo triangular con una base de 4 pulgadas y una altura de 3 pulgadas. La longitud de cada lado es de 5 pulgadas y el ancho de cada lado es de 3 pulgadas. ¿Cuál es la superficie del prisma?
- Un prisma triangular tiene un extremo triangular con una base de 4 pies y una altura de 5 pies. La longitud de cada lado es de 6 pies y el ancho de cada lado es de 5 pies. ¿Cuál es la superficie del prisma?
- Un prisma triangular tiene un extremo triangular con una base de 3 pulgadas y una altura de 3 pulgadas. La longitud de cada lado es de 4 pulgadas y el ancho de cada lado es de 3 pulgadas. ¿Cuál es la superficie del prisma?
- Un prisma triangular tiene un extremo triangular con una base de 6 metros y una altura de 5 metros. La longitud de cada lado es de 8 metros y el ancho de cada lado es de 5 metros. ¿Cuál es la superficie del prisma?
- Un prisma triangular tiene un extremo triangular con una base de 15 pies y una altura de 10 pies. La longitud de cada lado es de 12 pies y el ancho de cada lado es de 10 pies. ¿Cuál es la superficie del prisma?
- Un prisma triangular tiene un extremo triangular con una base de 9 pulgadas y una altura de 7 pulgadas. La longitud de cada lado es de 9 pulgadas y el ancho de cada lado es de 7 pulgadas. ¿Cuál es la superficie del prisma?
- Un prisma triangular tiene un extremo triangular con una base de 8 pulgadas y una altura de 6 pulgadas. La longitud de cada lado es de 15 pulgadas y el ancho de cada lado es de 6 pulgadas. ¿Cuál es la superficie del prisma?
- Un prisma triangular tiene un extremo triangular con una base de 5.5 pies y una altura de 4 pies. La longitud de cada lado es de 9 pies y el ancho de cada lado es de 5 pies. ¿Cuál es la superficie del prisma?
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 10.5.
Recursos
vocabulario
| Término | Definición |
|---|---|
| Área | Área es el espacio dentro del perímetro de una figura bidimensional. |
| Prisma | Un prisma es un objeto tridimensional con dos bases paralelas congruentes que son polígonos. |
| Superficie | El área superficial es el área total de todas las superficies de un objeto tridimensional. |
| Prisma Triangular | Un prisma triangular es un prisma compuesto por dos bases triangulares y tres caras rectangulares. |
Recursos adicionales
Elemento Interactivo
Video: Encontrar el área de superficie de una caja superior abierta
Práctica: Superficie de Prismas

