9.16: Superficie y Volumen de Pirámides
- Page ID
- 107241
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Área superficial y volumen de sólidos con una base y caras laterales que se encuentran en un vértice común.
Pirámides
Una pirámide es un sólido con una base y caras laterales que se encuentran en un vértice común . Los bordes entre las caras laterales son bordes laterales . Los bordes entre la base y las caras laterales son bordes de base .

Una pirámide regular es una pirámide donde la base es un polígono regular. Todas las pirámides regulares también tienen una altura inclinada, que es la altura de una cara lateral. Una pirámide no regular no tiene una altura inclinada.

Superficie
El área superficial es una medida bidimensional que es el área total de todas las superficies que unen un sólido. La unidad básica de área es la unidad cuadrada. Para las pirámides, necesitaremos usar la altura inclinada, que está etiquetada como l, para encontrar el área de cada cara triangular.
Superficie de una Pirámide Regular: Si B es el área de la base, y n es el número de triángulos, entonces\(SA=B+\dfrac{1}{2}nbl\).
La red muestra la superficie de una pirámide. Si alguna vez olvidas la fórmula, usa la red.

Volumen
Para encontrar el volumen de cualquier sólido debes averiguar cuánto espacio ocupa. La unidad básica de volumen es la unidad cúbica.
Volumen de una Pirámide:\(V=\dfrac{1}{3}Bh\) dónde\(B\) está el área de la base.

¿Y si te dieran una figura tridimensional sólida con una base y caras laterales que se encuentran en un vértice común? ¿Cómo podrías determinar cuánto espacio bidimensional y tridimensional ocupa esa figura?
Ejemplo\(\PageIndex{1}\)
Encuentra la altura inclinada de la pirámide cuadrada.

Solución
La altura inclinada es la hipotenusa del triángulo rectángulo formado por la altura y la mitad de la longitud de la base. Usa el Teorema de Pitágoras.
\(\begin{aligned} 8^{2}+24^{2}&=l^{2} \\ 640&=l^{2} \\ l=\sqrt{640}&=8\sqrt{10}\end{aligned}\)
Ejemplo\(\PageIndex{2}\)
Encuentra el área de superficie de la pirámide triangular regular.

Solución
“Regular” nos dice que la base es un triángulo equilátero. Dibujémoslo y encontremos su área.

\(B=\dfrac{1}{2}\cdot 8\cdot 4\sqrt{3}=16\sqrt{3}\)
La superficie es:
\(SA=16\sqrt{3}+\dfrac{1}{2}\cdot 3\cdot 8\cdot 18=16\sqrt{3}+216\approx 243.71\)
Ejemplo\(\PageIndex{3}\)
Si el área de superficie lateral de una pirámide cuadrada regular es\(72\: ft^{2}\) y el borde base es igual a la altura inclinada. ¿Cuál es la longitud del borde base?
Solución
En la fórmula para el área de superficie, el área de superficie lateral es\(\dfrac{1}{2}nbl\). Eso lo sabemos\(n=4\) y\(b=l\). Vamos a resolver para\(b\).
\(\begin{aligned} \dfrac{1}{2}nbl&=72\text{ ft}^{2} \\ \dfrac{1}{2}(4)b^{2}&=7^{2} \\ 2b^{2}&=7^{2} \\ b^{2}&=36\\ b&=6 \text{feet}\end{aligned}\)
Ejemplo\(\PageIndex{4}\)
Encuentra la altura y luego el volumen de la pirámide.

Solución
En este ejemplo, se nos da la altura inclinada. Usa el Teorema de Pitágoras.
\(\begin{aligned} 7^{2}+h^{2}&=25^{2} \\ h^{2}&=576 \\ h&=24\end{aligned}\)
\(V=13(142)(24)=1568\text{ units}^{3}\)
Ejemplo\(\PageIndex{5}\)
Encuentra el volumen de la pirámide con un triángulo rectángulo como base.
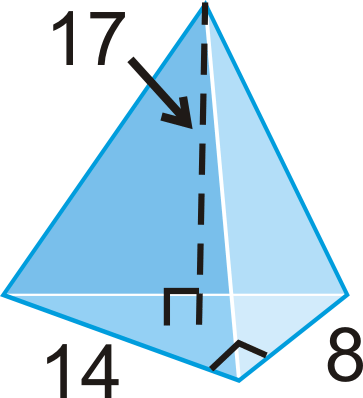
Solución
La base de la pirámide es un triángulo rectángulo. El área de la base es\(\dfrac{1}{2}(14)(8)=56\text{ units}^{2}\).
\(V=\dfrac{1}{3}(56)(17)\approx 317.33\text{ units}^{3}\)
Ejemplo\(\PageIndex{6}\)
Una pirámide rectangular tiene un área base de\(56\: cm^{2}\) y un volumen de\(224\: cm^{3}\). ¿Cuál es la altura de la pirámide?
Solución
Usa la fórmula para el volumen y conecta la información que nos dieron. Entonces resuelve para la altura.
\(\begin{aligned} V&=\dfrac{1}{3}Bh \\ 224&=\dfrac{1}{3}\cdot 56h \\ 12&=h \end{aligned}\)
Revisar
Rellene los espacios en blanco sobre el diagrama a la izquierda.

- x es el ___________.
- La altura inclinada es ________.
- y es el ___________.
- La altura es ________.
- La base es _______.
- El borde base es ________.
Para las preguntas 7-8, esboce cada uno de los siguientes sólidos y responda la pregunta. Tus dibujos deben ser a escala, pero no uno a uno. Deja tu respuesta en forma radical más simple.
- Dibuja una pirámide cuadrada con una longitud de borde de 9 pulgadas y una altura de 12 pulgadas. Encuentra la altura inclinada.
- Dibuja una pirámide triangular equilátera con una longitud de borde de 6 cm y una altura de 6 cm. ¿Cuál es la altura de la base?
Encuentra la altura inclinada, l, de una cara lateral en cada pirámide. Redondee su respuesta a la centésima más cercana.
-

Figura\(\PageIndex{11}\) -

Figura\(\PageIndex{12}\)
Encuentra el área de superficie y el volumen de la pirámide regular. Redondee sus respuestas a la centésima más cercana.
-

Figura\(\PageIndex{13}\) -

Figura\(\PageIndex{14}\) -

Figura\(\PageIndex{15}\) -

Figura\(\PageIndex{16}\) -
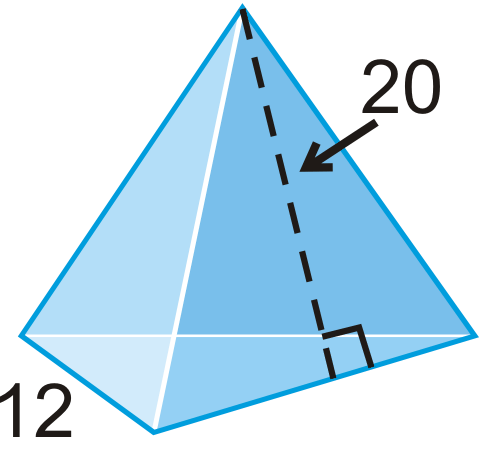
Figura\(\PageIndex{17}\) -

Figura\(\PageIndex{18}\) - Un tetraedro regular tiene cuatro triángulos equiláteros como sus caras.
- Encuentra la altura de una de las caras si la longitud del borde es de 6 unidades.
- Encuentra el área de una cara.
- Encuentra la superficie total del tetraedro regular.
- Si el área de superficie de una pirámide cuadrada es\(40\text{ ft}^{2}\) y el borde base es de 4 pies, ¿cuál es la altura inclinada?
- Si el área lateral de una pirámide cuadrada es\(800\text{ in}^2\) y la altura inclinada es de 16 pulgadas, ¿cuál es la longitud del borde base?
- Si el área lateral de una pirámide triangular regular es\(252\text{ in}^2\) y el borde base es de 8 pulgadas, ¿cuál es la altura inclinada?
- El volumen de una pirámide cuadrada es de 72 pulgadas cuadradas y el borde base es de 4 pulgadas. ¿Cuál es la altura?
- El volumen de una pirámide triangular es\(170\text{ in}^3\) y el área base es\(34\text{ in}^2\). ¿Cuál es la altura de la pirámide?
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 11.5.
El vocabulario
| Término | Definición |
|---|---|
| bordes laterales | Bordes entre las caras laterales de un prisma. |
| caras laterales | Las caras no base de un prisma. |
| Pyramid | Una pirámide es un objeto tridimensional con una base que es un polígono y caras triangulares que se encuentran en un vértice. |
| pirámide regular | es una pirámide donde la base es un polígono regular. Todas las pirámides regulares también tienen una altura inclinada, que es la altura de una cara lateral. |
| Cono | Un cono es una figura tridimensional sólida con una base circular y un vértice. |
| Vertex | Un vértice es un punto de intersección de las líneas o rayos que forman un ángulo. |
| Volumen | El volumen es la cantidad de espacio dentro de los límites de un objeto tridimensional. |
| Principio de Cavalieri | Afirma que si dos sólidos tienen la misma altura y la misma área de sección transversal en cada nivel, entonces tendrán el mismo volumen. |
| Borde base | El borde base es el borde entre la base y las caras laterales de un prisma. |
| Altura Inclinada | La altura inclinada es la altura de una cara lateral de una pirámide. |
| Apothem | El apotema de un polígono regular es un segmento perpendicular desde el punto central del polígono hasta el punto medio de uno de sus lados. |

