9.17: Volumen de pirámides
- Page ID
- 107263
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)El volumen es igual al área de los tiempos base\(\dfrac{1}{3}\) de altura.

Michael y Juanita están interesados en la cantidad de arena requerida para construir una pirámide de arena del tamaño que ven mientras están en una exhibición de esculturas de arena. Miden cuidadosamente el ancho de la base cuadrada de la pirámide de arena que es de 4 pies y la altura de la pirámide que es de 5 pies. ¿Cuánta arena se requiere para construir esta pirámide de arena?
En este concepto, aprenderás a calcular el volumen de una pirámide.
Encontrar el volumen de una pirámide
Las pirámides son formas sólidas que existen en el espacio tridimensional. Una pirámide tiene lados que son caras triangulares y una base que puede ser de cualquier forma.

El volumen es la medida de cuánto espacio ocupa o retiene una figura tridimensional. El volumen se mide en unidades cúbicas, porque se trata de tres dimensiones: largo, ancho y alto.
Se puede comenzar a entender el volumen de una pirámide comparando una pirámide con una figura que es similar a ella. Sabes que un prisma tiene largo, ancho y alto. Las bases paralelas de un prisma pueden ser cualquier polígono. Este tiene una base cuadrada; por lo que se llama cubo.

Ahora piensa en una pirámide. Tiene una base que puede ser cualquier polígono. La base de esta pirámide es un cuadrado.

Estos son ambos similares dado que tienen bases cuadradas. Piensa en el volumen de una pirámide mirando el volumen del cubo o prisma. Mira esta imagen que demuestra la relación de un cubo con una pirámide cuadrada:

Para encontrar el volumen de este cubo, multiplique la base por el ancho por la altura. Para encontrar el volumen de la pirámide, toma el área de la base,\(B\) y multiplícala por la altura y luego multiplícala por\(\dfrac{1}{3}\). Aquí está la fórmula para encontrar el volumen de una pirámide.
\(\(V=\dfrac{1}{3}Bh\)
Una cosa a tener en cuenta es que las pirámides pueden ser complicadas porque pueden tener muchas bases diferentes. \(B\)en la fórmula significa que necesitas encontrar el área de la base. Si la base es un cuadrado, necesitará usar la fórmula para el área de un cuadrado,\(B=s^2\). Si la base es un rectángulo, el área de la base es\(B=lw\). Si la base es un triángulo, usa la fórmula\(B=\dfrac{bh}{2}\). Asegurarse de tener la fórmula correcta es esencial en su trabajo con pirámides.
Veamos un ejemplo. ¿Cuál es el volumen de la pirámide a continuación?
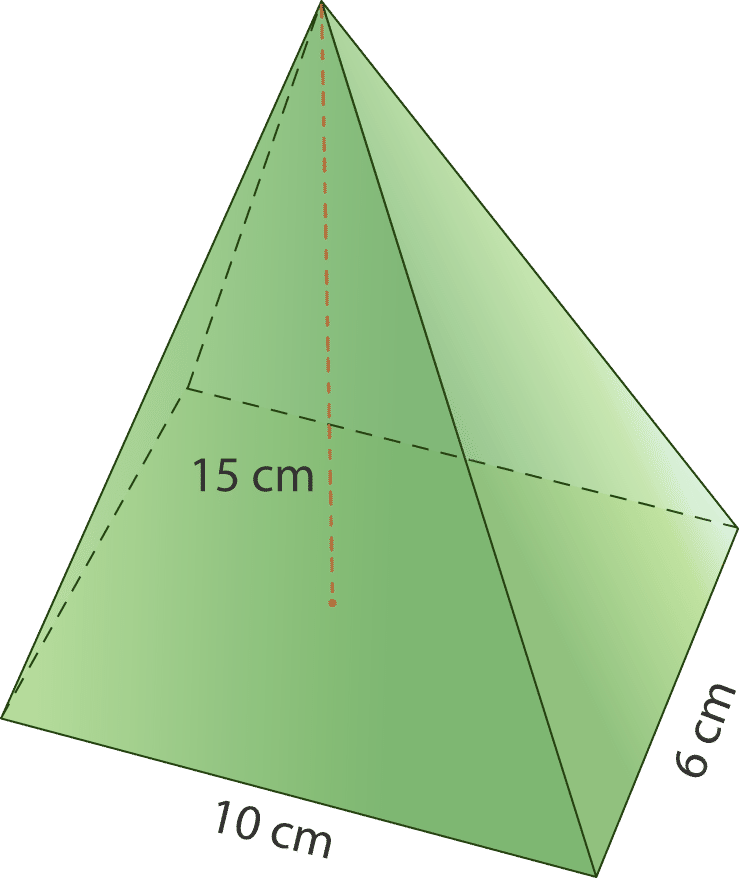
Primero, decide qué forma es la base de la pirámide. Un lado mide 10 centímetros y el otro mide 6 centímetros, por lo que debe ser un rectángulo. Usa la fórmula de área para rectángulos para encontrar B, el área base.
\(\begin{aligned} B&=lw \\ B&=10(6) \\ B&=60\text{ cm}^{2}\end{aligned}\)
El área de la base de esta pirámide es de 60 centímetros cuadrados. Ahora multiplica esto por la altura y 13 según la fórmula.
\(\begin{aligned} V&=\dfrac{1}{3}Bh \\ V&=\dfrac{1}{3}(60)(15) \\ V&=\dfrac{900}{3} \\ V&=300\text{ cm}^{3}\end{aligned}\)
La respuesta es que el volumen de la pirámide es de 300 centímetros cúbicos.
Recuerda, mides el volumen en tres dimensiones, así que escribe la respuesta en unidades cúbicas.
Veamos otro ejemplo.
Encuentra el volumen de la figura a continuación.

Esta vez la base es un triángulo, por lo que necesitarás usar la fórmula de área para que los triángulos encuentren el área base. Tenga cuidado de no confundir la altura del triángulo base con la altura de toda la pirámide.
\(\begin{aligned} B&=\dfrac{1}{2}bh\\ B&=\dfrac{1}{2}(8)(3) \\ B&=\dfrac{24}{2} \\ B&=12 in^{2}\end{aligned}\)
El área base para esta pirámide triangular es de 12 pulgadas cuadradas. Pon esto en la fórmula y resuelve para V, volumen.
\(\begin{aligned} V&=\dfrac{1}{3}Bh \\ V&=\dfrac{1}{3}(12)(17) \\ V&=\dfrac{204}{3} \\ V&=68\text{ in}^{3}\end{aligned}\)
La respuesta es que el volumen de esta pirámide es de 68 pulgadas cúbicas.
Ejemplo\(\PageIndex{1}\)
Anteriormente, se le dio un problema sobre el interés de Michael y Juanita en la pirámide de escultura de arena.
Quieren averiguar el volumen de arena requerido para crear una pirámide de escultura de arena con base 4 pies y altura 5 pies:
Solución
Primero, determine la forma de la base y use la fórmula correcta para encontrar el área base. Dado que la base es un cuadrado, use la fórmula de área para cuadrados para encontrar el área base.
\(\begin{aligned} B&=s^{2} \\ B&=(4)^{2} \\ B&=16\text{ ft}^{2}\end{aligned}\)
El área base de la pirámide es de 16 centímetros cuadrados.
A continuación, conecte el área de la base, y la altura de la pirámide en la fórmula para el volumen de una pirámide y multiplique los valores juntos.
\(\begin{aligned} V&=\dfrac{1}{3}Bh \\ V&=\dfrac{1}{3}(16)(5) \\ V&=803\end{aligned}\)
Luego, divida por 3 para la respuesta, asegurándose de incluir la unidad de medida apropiada.
\(\begin{aligned}V&=803 \\ V&=26.67\text{ ft}^{3}\end{aligned}\)
La respuesta es que el volumen de arena requerido para crear la pirámide de escultura de arena es de 26.67 pies cúbicos.
Ejemplo\(\PageIndex{2}\)
Felice compró la vela de abajo para el cumpleaños de su amiga. El paquete dice que la vela quema una hora por cada 20 centímetros cúbicos de cera. ¿Cuál es el volumen de la vela para que Felice pueda averiguar cuánto tiempo va a quemar?

Solución
Primero, determine la forma de la base y use la fórmula correcta para encontrar el área base. Dado que la base es un cuadrado, usa la fórmula de área para cuadrados para encontrar el área base.
\(\begin{aligned}B&=s^{2} \\ B&=(12)^{2} \\ B&=144\text{ cm}^{2}\end{aligned}\)
El área base de la pirámide es de 144 centímetros cuadrados.
A continuación, conecte el área de la base, y la altura de la pirámide en la fórmula para el volumen de una pirámide y multiplique los valores juntos.
\(\begin{aligned} V&=\dfrac{1}{3}Bh \\ V&=\dfrac{1}{3}(144)(24) \\ V&=\dfrac{3456}{3}\end{aligned}\)
Luego, divida por 3 para la respuesta, asegurándose de incluir la unidad de medida apropiada.
\(\begin{aligned} V&=\dfrac{3456}{3} \\ V&=1,152\text{ cm}^{3}\end{aligned}\)
La respuesta es que el volumen de la vela es de 1,152 cm cúbicos.
Ejemplo\(\PageIndex{3}\)
Encuentra el volumen de una pirámide cuadrada con una base de 8 cm y una altura de 6 cm.
Solución
Primero, determine la forma de la base y use la fórmula correcta para encontrar el área base. La base es un cuadrado, así que usa la fórmula de área para cuadrados para encontrar el área base.
\(\begin{aligned} B&=s^{2} \\ B&=(8)^{2} \\ B&=64\text{ cm}^{2}\end{aligned}\)
El área base de la pirámide es de 64 centímetros cuadrados.
A continuación, conecte el área de la base, y la altura de la pirámide en la fórmula para el volumen de una pirámide y multiplique los valores juntos.
\(\begin{aligned} V&=\dfrac{1}{3}Bh \\ V&=\dfrac{1}{3}(64)(6) \\ V&=\dfrac{384}{3}\end{aligned} \)
Luego, divida por 3 para la respuesta, asegurándose de incluir la unidad de medida apropiada.
\(\begin{aligned} V&=\dfrac{384}{3} \\ V&=128\text{ cm}^{3}\end{aligned}\)
La respuesta es que el volumen de la pirámide es de 128 cm cúbicos.
Ejemplo\(\PageIndex{4}\)
Encuentra el volumen de una pirámide rectangular con una longitud de 10 cm, un ancho de 8 cm y una altura de 9 cm.
Solución
Primero, determine la forma de la base y use la fórmula correcta para encontrar el área base. Dado que la base es un rectángulo, use la fórmula de área para cuadrados para encontrar el área base.
\(\begin{aligned} B&=lw \\ B&=(10)(8) \\ B&=80\text{ cm}^{2}\end{aligned}\)
El área base de la pirámide es de 80 centímetros cuadrados.
A continuación, conecte el área de la base, y la altura de la pirámide en la fórmula para el volumen de una pirámide y multiplique los valores juntos.
\(\begin{aligned} V&=\dfrac{1}{3}Bh \\ V&=\dfrac{1}{3}(80)(9) \\ V&=\dfrac{720}{3}\end{aligned}\)
Luego, divida por 3 para la respuesta, asegurándose de incluir la unidad de medida apropiada.
\(\begin{aligned} V&=\dfrac{720}{3} \\ V&=240\text{ cm}^{3}\end{aligned}\)
La respuesta es que el volumen de la pirámide es de 240 cm cúbicos.
Ejemplo\(\PageIndex{5}\)
Encuentra el volumen de una pirámide cuadrada con una base de 5.5 pulgadas y una altura de 4 pulgadas.
Solución
Primero, determine la forma de la base y use la fórmula correcta para encontrar el área base. La base es un cuadrado, así que usa la fórmula de área para cuadrados para encontrar el área base.
\(\begin{aligned} B&=s^{2} \\ B&=(5.5)^{2} \\ B&=30.25 in^{2}\end{aligned} \)
El área base de la pirámide es de 30.25 centímetros cuadrados.
A continuación, conecte el área de la base, y la altura de la pirámide en la fórmula para el volumen de una pirámide y multiplique los valores juntos.
\(\begin{aligned} V&=\dfrac{1}{3}Bh \\ V&=\dfrac{1}{3}(30.25)(4) \\ V&=\dfrac{121}{3}\end{aligned}\)
Luego, divida por 3 para la respuesta, asegurándose de incluir la unidad de medida apropiada.
\(\begin{aligned} V&=\dfrac{121}{3} \\ V&=40.33\text{ in}^{3}\end{aligned}\)
La respuesta es que el volumen de la pirámide es de 40.33 pulgadas cúbicas.
Revisar
Encuentra el volumen de cada una de las siguientes pirámides.
- Una pirámide cuadrada con una base de 6 pies y una altura de 9 pies.
- Una pirámide cuadrada con una base de 8 m y una altura de 10 m.
- Una pirámide cuadrada con una base de 11 pulgadas y una altura de 13 pulgadas.
- Una pirámide cuadrada con una base de 9 pies y una altura de 14 pies.
- Una pirámide cuadrada con una base de 4.5 pulgadas y una altura de 5 pulgadas.
- Una pirámide rectangular con una longitud de base de 4 pulgadas, un ancho de base de 3 pulgadas y una altura de 5 pulgadas.
- Una pirámide rectangular con una longitud de base de 5 pies, un ancho de base de 4 pies y una altura de 6 pies.
- Una pirámide rectangular con una longitud de base de 7 m, un ancho de base de 4 m y una altura de 9 m.
- Una pirámide triangular con una longitud de base de 5 pulgadas y una altura de base de 4 pulgadas con una altura de pirámide de 6 pulgadas.
- Una pirámide triangular con una longitud de base de 8 pies y una altura base de 7 pies con una altura de pirámide de 9 pies.
- Una pirámide cuadrada con una base de 8 pies y una altura de 4 pies.
- Una pirámide rectangular con una longitud de 5 pulgadas, un ancho de 4 pulgadas y una altura de 6 pulgadas.
- Una pirámide cuadrada con una base de 3.5 pies y una altura de 6.5 pies.
- Una pirámide cuadrada con una base de 6.5 pies y una altura de 8.5 pies.
- Una pirámide rectangular con un ancho de 4 pies, una longitud de 6 pies y una altura de 7.5 pies.
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 10.14.
El vocabulario
| Término | Definición |
|---|---|
| Cono | Un cono es una figura tridimensional sólida con una base circular y un vértice. |
| Pyramid | Una pirámide es un objeto tridimensional con una base que es un polígono y caras triangulares que se encuentran en un vértice. |
| Volumen | El volumen es la cantidad de espacio dentro de los límites de un objeto tridimensional. |
Recursos adicionales
Elemento Interactivo
Video: Volumen de una pirámide - Descripción general
Práctica: Volumen de pirámides

