9.18: Superficie y Volumen de Cilindros
- Page ID
- 107273
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Superficie y volumen de sólidos con bases circulares congruentes en planos paralelos.
Cilindros
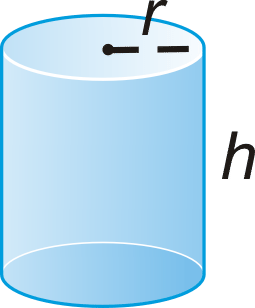
Un cilindro es un sólido con bases circulares congruentes que se encuentran en planos paralelos. El espacio entre los círculos está encerrado.
Un cilindro tiene un radio y una altura .
Un cilindro también puede ser oblicuo (inclinado) como el de abajo.
Superficie
El área de superficie es la suma del área de las caras de un sólido. La unidad básica de área es la unidad cuadrada.
Área de superficie de un cilindro derecho:\(SA=2 \pi r^{2}+2 \pi r h\).
\(\underbrace{2 \pi r^{2}}_\text{area of both circles}+ \underbrace{2 \pi r h}_\text{length of rectangle}\)
Volumen
Para encontrar el volumen de cualquier sólido debes averiguar cuánto espacio ocupa. La unidad básica de volumen es la unidad cúbica. Para los cilindros, el volumen es el área de la base circular multiplicada por la altura.
Volumen de un cilindro:\(V= \pi r^{2}h\)
Si un cilindro oblicuo tiene la misma área base y altura que otro cilindro, entonces tendrá el mismo volumen. Esto se debe al Principio de Cavalieri, que establece que si dos sólidos tienen la misma altura y la misma área de sección transversal en cada nivel, entonces tendrán el mismo volumen.
¿Y si te dieran una figura tridimensional sólida con bases circulares encerradas congruentes que están en planos paralelos? ¿Cómo podrías determinar cuánto espacio bidimensional y tridimensional ocupa esa figura?
Ejemplo\(\PageIndex{1}\)
Si el volumen de un cilindro es\(484 \pi in^{3}\) y la altura es de 4 pulgadas, ¿cuál es el radio?
Solución
Resolver para\(r\).
\(\begin{aligned} 484 \pi&= \pi r^{2}(4) \\ 121&=r^{2} \\ 11\text{ in}&=r\end{aligned}\)
Ejemplo\(\PageIndex{2}\)
La circunferencia de la base de un cilindro es\(80 \pi\) cm y la altura es de 36 cm. Encuentra la superficie total.
Solución
Tenemos que resolver para el radio, usando la circunferencia.
\(\begin{aligned} 2 \pi r&=80 \pi \\ r&=40\end{aligned}\)
Ahora, podemos encontrar la superficie.
\(\begin{aligned} SA&=2 \pi(40)^{2}+(80 \pi)(36) \\ &=3200 \pi+2880 \pi \\ &=6080 \pi \text{ units}^{2}\end{aligned}\)
Ejemplo\(\PageIndex{3}\)
Encuentra la superficie del cilindro.
Solución
\(r=4\)y\(h=12\).
\(\begin{aligned} SA&=2 \pi(4)^{2}+2 \pi(4)(12) \\ &=32 \pi+96 \pi \\ &=128 \pi \text{ units}^{2}\end{aligned} \)
Ejemplo\(\PageIndex{4}\)
La circunferencia de la base de un cilindro es\(16 \pi\) y la altura es 21. Encuentra la superficie del cilindro.
Solución
Tenemos que resolver para el radio, usando la circunferencia.
\(\begin{aligned} 2 \pi r&=16 \pi \\ r&=8\end{aligned}\)
Ahora, podemos encontrar la superficie.
\(\begin{aligned} SA&=2 \pi(8)2+(16 \pi)(21) \\ &=128 \pi+336 \pi \\ &=464 \pi \text{ units}^{2}\end{aligned}\)
Ejemplo\(\PageIndex{5}\)
Encuentra el volumen del cilindro.
Solución
Si el diámetro es 16, entonces el radio es 8.
\(\begin{aligned} V&= \pi 8^{2}(21) \\ &=1344 \pi \text{ units}^{3}\end{aligned}\)
Revisar
- Dos cilindros tienen la misma superficie. ¿Tienen el mismo volumen? ¿Cómo lo sabes?
- Un cilindro tiene\(r=h\) y el radio es de 4 cm. ¿Cuál es el volumen?
- Un cilindro tiene un volumen de\(486 \pi \text{ ft}^{3}\). Si la altura es de 6 pies, ¿cuál es el diámetro?
- Un cilindro derecho tiene un radio de 7 cm y una altura de 18 cm. Encuentra el volumen.
Encuentra el volumen de los siguientes sólidos. Redondee sus respuestas a la centésima más cercana.
-
Figura\(\PageIndex{7}\) -
Figura\(\PageIndex{8}\)
Encuentra el valor de x, dado el volumen.
- \(V=6144 \pi \text{ units}^{3}\)
Figura\(\PageIndex{9}\) - El área de la base de un cilindro es\(49 \pi \text{ in}^{2}\) y la altura es de 6 pulgadas. Encuentra el volumen.
- La circunferencia de la base de un cilindro es\(34 \pi \text{ cm}\) y la altura es de 20 cm. Encuentra la superficie total.
- La superficie lateral de un cilindro es\(30 \pi \text{ m}^{2}\) y la altura es de 5 m. ¿Cuál es el radio?
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 11.4.
El vocabulario
| Término | Definición |
|---|---|
| cilindro | Un sólido con bases circulares congruentes que se encuentran en planos paralelos. El espacio entre los círculos está encerrado. Un cilindro tiene un radio y una altura y también puede ser oblicuo (inclinado). |
| Superficie | El área superficial es el área total de todas las superficies de un objeto tridimensional. |
| Volumen | El volumen es la cantidad de espacio dentro de los límites de un objeto tridimensional. |
| Principio de Cavalieri | Afirma que si dos sólidos tienen la misma altura y la misma área de sección transversal en cada nivel, entonces tendrán el mismo volumen. |
| Cilindro oblicuo | Un cilindro oblicuo es un cilindro con bases que no están directamente encima unas de otras. |
Recursos adicionales
Elemento Interactivo
Video: Principios de Cilindros - Básicos
Actividades: Cilindros Discusión Preguntas
Ayudas de estudio: Guía de estudio de prismas y cilindros
Práctica: Superficie y Volumen de Cilindros
Mundo real: Equipos de perforación