9.19: Superficie de Cilindros
- Page ID
- 107337
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)\(SA=2 \pi r(h+r)\)
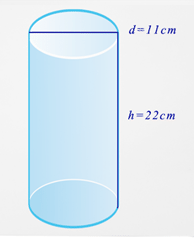
La señora Johnson está envolviendo un paquete cilíndrico en papel marrón para que pueda enviarlo por correo a su hijo. En base a las dimensiones que se muestran, ¿cuánto papel necesitará para cubrir el paquete?
En este concepto, aprenderás a encontrar la superficie de los cilindros.
Superficie
Un cilindro tiene dos bases circulares congruentes paralelas con un rectángulo curvo como su lado. Una forma es usar una red.
Una red es un diagrama bidimensional de una figura tridimensional. Si pudieras desplegar un cilindro (como una lata) para que quede completamente plano, tendrías algo que se vea así.

Con la red de un cilindro, se necesitaría calcular el área de cada círculo y el área del lado curvo del cilindro. Entonces podrías sumar estos valores juntos para encontrar la k.
La fórmula se\(A&= \pi r^{2}\) puede utilizar para encontrar el área de un círculo bases. Vuelva a mirar de cerca el cilindro de arriba. Las dos caras circulares son congruentes, por lo que deben tener el mismo radio y diámetro.
Veamos un ejemplo.

Primero, calcule el área de las bases circulares.
\(\begin{aligned} A&= \pi r^{2}\\ A&= \pi (4)^{2} \\ A&= \pi (16) \\ A&=50.3\end{aligned}\)
A continuación, encuentra la longitud del lado del cilindro. Sabes que el ancho es de 8 cm pero no se muestra el largo. Se desenvolvió el cilindro para formar la red. Por lo tanto, la circunferencia del círculo sería la longitud del lado.
\(\begin{aligned}C&=2 \pi r \\ C&=2 \pi \times 4 \\ C&=25.1\end{aligned}\)
Después, calcula el área del costado.
\(\begin{aligned}A&=l\times w \\ A&=25.1\times 8 \\ A&=200.8\end{aligned}\)
Luego, encuentra el área de superficie del cilindro agregando el área lateral al área superior e inferior.
\(\begin{aligned}SA&=bottom+top+side \\ SA&=50.3+50.3+200.8 \\ SA&=301.4\end{aligned}\)
La respuesta es 301.4.
La superficie del cilindro es\(301.4 \text{ cm}^{2}\).
Al juntar todo esto, puede usar la siguiente fórmula para encontrar el área de superficie del cilindro:
\(SA=2 \pi r^{2}+2 \pi rh\)
La fórmula\(2 \pi r^{2}\) representa el área de los círculos superior e inferior del cilindro. El\(2 \pi r h\) representa el perímetro (\(2 \pi r\)) multiplicado por la altura,\(h\).
Veamos un ejemplo.
¿Cuál es la superficie de la figura a continuación?
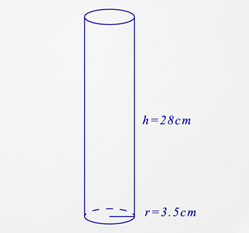
Primero, sustituya lo que sabes en la fórmula de área de superficie.
\(\begin{aligned}SA&=2 \pi r^{2}+2 \pi r h \\ SA&=2 \pi (3.5)^{2}+2 \pi (3.5)(28)\end{aligned}\)
A continuación, calcule el área de superficie.
\(\begin{aligned}SA&=2 \pi (3.5)^{2}+2 \pi (3.5)(28) \\ SA&=2 \pi (12.25)+2 \pi (98) \\ SA&=76.97+615.75 \\ SA&=692.72\end{aligned}\)
La respuesta es 692.72.
La superficie del cilindro es\(692.7 \text{ cm}^{2}\).
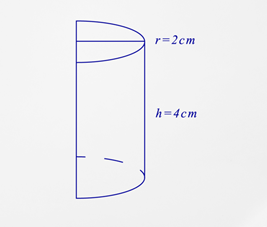
En ocasiones, se puede tener un cilindro que ha sido cortado. A esto se le llama un cilindro truncado. Aquí es donde solo ves una sección del cilindro y necesitarás averiguar la superficie de lo que ves.
Ejemplo\(\PageIndex{1}\)
Anteriormente, le dieron un problema sobre el envoltorio cilíndrico de la señora Johnson.
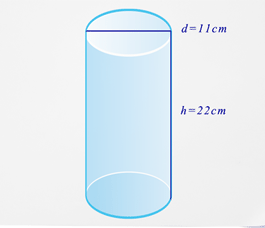
Solución
Primero, necesitas encontrar el radio. Recuerde, el radio es la mitad de la medida del diámetro.
\(\begin{aligned}r&=\dfrac{d}{2} \\ r&=\dfrac{11}{2} \\ r&=5.5v\end{aligned}\)
A continuación, sustituya lo que sabes en la fórmula de área de superficie.
\(\begin{aligned}SA&=2 \pi r^{2}+2 \pi rh \\ SA&=2 \pi (5.5)^{2}+2 \pi (5.5)(22)\end{aligned}\)
Después, calcule el área de superficie.
\(\begin{aligned}SA&=2 \pi (5.5)^{2}+2 \pi (5.5)(22) \\ SA&=2 \pi (30.25)+2 \pi (121) \\ SA&=190.1+760.3 \\ SA&=950.4\end{aligned}\)
La respuesta es 950.4.
La señora Johnson necesita\(950.4 \: cm^{2}\) papel marrón para envolver su paquete.
Ejemplo\(\PageIndex{2}\)
¿Cuál es la superficie de la figura a continuación?

Solución
Primero, necesitas encontrar el radio. Recuerda que el radio es la mitad de la medida del diámetro.
\(\begin{aligned}r&=\dfrac{d}{2} \\ r&=\dfrac{13}{2} \\ r&=6.5\end{aligned}\)
A continuación, sustituya lo que sabes en la fórmula de área de superficie.
\(\begin{aligned}SA&=2 \pi r^{2}+2 \pi rh \\ SA&=2 \pi (6.5)^{2}+2 \pi (6.5)(11)\end{aligned}\)
Después, calcule el área de superficie.
\(\begin{aligned}SA&=2 \pi (6.5)^{2}+2 \pi (6.5)(11) \\ SA&=2 \pi (42.25)+2 \pi (71.5) \\ SA&=265.5+449.2 \\ SA&=714.7\end{aligned}\)
La respuesta es 714.7.
El área superficial del cilindro es\ (714.7\: ft^ {2}.
Ejemplo\(\PageIndex{3}\)
Encuentra el área de superficie de un cilindro con un radio de 6 pulgadas y una altura de 5 pulgadas.
Solución
Primero, sustituya lo que sabes en la fórmula de área de superficie.
\(\begin{aligned}SA&=2 \pi r^{2}+2 \pi rh \\ SA&=2 \pi (6)^{2}+2 \pi (6)(5)\end{aligned}\)
A continuación, calcule el área de superficie.
\(\begin{aligned} SA&=2 \pi (6)^{2}+2 \pi (6)(5) \ SA&=2 \pi (36)+2 \pi (30) \\ SA&=226.2+188.5 \\ SA&=414.7\end{aligned}\)
La respuesta es 414.7.
La superficie del cilindro es\(414.7 \: in^{2}\).
Ejemplo\(\PageIndex{4}\)
Encuentra la superficie de un cilindro con un radio de 4 cm y una altura de 12 cm.
Solución
Primero, sustituya lo que sabes en la fórmula de área de superficie.
\(SA&=2 \pi r^{2}+2 \pi rh \\ SA&=2 \pi (4)^{2}+2 \pi (4)(12)\end{aligned}\)
A continuación, calcule el área de superficie.
\(\begin{aligned} SA&=2 \pi (4)^{2}+2 \pi (4)(12) \\ SA&=2 \pi (16)+2 \pi (48) \\ SA&=100.5+301.6 \\ SA&=402.1\end{aligned}\)
La respuesta es 402.1.
La superficie del cilindro es\(402.1 \: cm^{2}\).
Ejemplo\(\PageIndex{5}\)
Encuentra la superficie de un cilindro con un diámetro de 10 metros y una altura de 15 metros.
Solución
Primero, necesitas encontrar el radio. Recuerda que el radio es la mitad de la medida del diámetro.
\(\begin{aligned} r&=\dfrac{d}{2} \\ r&=\dfrac{10}{2} \\ r&=5\end{aligned}\)
A continuación, sustituya lo que sabes en la fórmula de área de superficie.
\(\begin{aligned} SA&=2 \pi r^{2}+2 \pi r h \\ SA&=2 \pi (5)^{2}+2 \pi (5)(15)\end{aligned}\)
Después, calcule el área de superficie.
\(\begin{aligned}SA&=2 \pi (5)^{2}+2 \pi (5)(15) \\ SA&=2 \pi (25)+2 \pi (75) \\ SA&=157.1+471.2 \\ SA&=628.3\end{aligned}\)
La respuesta es 628.3.
La superficie del cilindro es\(628.3 \: m^{2}\).
Revisar
Usa los diagramas para responder a las preguntas que se encuentran debajo de cada una.

- ¿Cuál es el nombre de esta figura?
- ¿Cuál es la forma de la base de esta figura?
- ¿Cuántas bases hay?
- ¿Cuál es la superficie de esta figura?
- ¿Qué medida se necesita el radio o el diámetro?

- ¿Cuál es el nombre de esta figura?
- ¿A qué medida se le da el radio o el diámetro?
- ¿Cuál es la superficie de la figura?
Usa lo que has aprendido para responder a cada pregunta.
- Un tanque de agua cilíndrico mide 35 de largo y 10 pies de ancho. ¿De qué cantidad de chapa está hecho el tanque?
- ¿Utilizó área o superficie para resolver este problema?
- Verdadero o falso. Solo puedes encontrar el área de superficie si conoces el volumen.
- Verdadero o falso. La superficie y el volumen miden lo mismo.
- Verdadero o falso. El área de superficie mide el exterior de un cilindro.
- Verdadero o falso. Necesita el radio para encontrar el área de superficie de un cilindro.
- Verdadero o falso. El radio es la mitad del diámetro.
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 8.7.
vocabulario
| Término | Definición |
|---|---|
| Cilindro | Un cilindro es una figura sólida con dos bases circulares congruentes paralelas. |
| Net | Una red es un diagrama que muestra una vista “aplanada” de un sólido. En una red, cada cara y base se muestra con todas sus dimensiones. Una red también puede servir como patrón para construir un sólido tridimensional. |
| Prisma | Un prisma es un objeto tridimensional con dos bases paralelas congruentes que son polígonos. |
| Superficie | El área superficial es el área total de todas las superficies de un objeto tridimensional. |
| Tridimensional | Una figura dibujada en tres dimensiones se dibuja utilizando longitud, anchura y altura o profundidad. |
| Cilindro Truncado | Un cilindro que se corta en parte de un cilindro completo. |
Recursos adicionales
Elemento Interactivo
Video: Volumen del cilindro y área de superficie
Práctica: Superficie de Cilindros
Mundo real: ¿Por qué flotan los superpetroleros?

