9.20: Volumen de Cilindros
- Page ID
- 107262
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)El volumen es igual al área de arriba o abajo veces la altura.

Ramona preparó una olla grande de conservas de frutas, pero se quedó sin frascos de conservas antes de haber enlatado todas las conservas. Ella sacó dos contenedores de almacenamiento de alimentos de la alacena. Los contenedores cilíndricos tienen las dimensiones que se indican a continuación. No hay suficiente de la reserva extra para ambos contenedores, por lo que solo necesita uno de los contenedores y tiene que ser el que tenga mayor volumen.

¿Cómo puede Ramona usar estas dimensiones para averiguar qué contenedor contendrá más?
En este concepto, aprenderás a usar fórmulas para encontrar el volumen de cilindros.
Encontrar el volumen de cilindros
Volumen es la cantidad de espacio contenido dentro de una figura sólida. En el caso de los cilindros, se puede pensar en el volumen como la capacidad, o la cantidad de un líquido o sustancia, que puede contener.
A diferencia de los prismas, los cubos unitarios no encajan muy bien en un cilindro.

Entonces, para calcular el volumen de un cilindro con precisión, es necesario usar una fórmula en lugar de cubos unitarios.
Para calcular el volumen de un cilindro, comience calculando el área de la base circular. Eso te dará una medida para el número de cubos unitarios que pueden caber en la parte inferior del cilindro. La altura del cilindro mostrará qué tan alto se pueden apilar los cubos dentro del cilindro.
Aquí está la fórmula para encontrar el volumen de un cilindro.
\(V&= \pi r^{2}h\)
Apliquemos esta fórmula.

El radio de la base circular es de 2 pulgadas. La altura del cilindro es de 7 pulgadas. Si tomas ambas medidas dadas y las sustitutas en la fórmula, puedes resolver por el volumen del cilindro.
\(\begin{aligned} V&= \pi r^{2} h \\ V&= (3.14)(2^{2})(7) \\ V&= (3.14)(4)(7) \\ V&= (3.14)(28) \\ V&= 87.92\text{ in}^{3}\end{aligned}\)
El volumen del cilindro es\(87.92\text{ in}^{3}\).
Ejemplo\(\PageIndex{1}\)
Antes, te dieron un problema sobre Ramona y su conserva extra de fruta.
Ramona tiene dos contenedores de almacenamiento de alimentos, pero no está seguro de cuál contendrá más. ¿Cómo puede Raymond usar estas dimensiones para averiguar cuál aguantará más?

Solución
Comienza con el contenedor de la izquierda.
Primero, tenga en cuenta que el diámetro es el doble del radio, así que divida el diámetro por 2 para obtener el radio.
8\ divide 2=4
El radio es 4.
A continuación, sustituya la información dada en la fórmula para luego resolver.
\(\begin{aligned}V&= \pi r^{2} h \\ V&= \pi (4)^{2} (16) \\ V&= \pi (16)(16) \\ V&= 256 \pi \\ V&= 803.84\text{ in}^{3}\end{aligned}\)
El primer contenedor tiene capacidad para 803.84 pulgadas cúbicas.
A continuación, considere el otro contenedor.
Primero, tenga en cuenta que el diámetro es el doble del radio, así que divida el diámetro por 2 para obtener el radio.
12\ divide 2=6
El radio es 6.
A continuación, sustituya la información dada en la fórmula para luego resolver.
\(\begin{aligned}V&= \pi r^{2} h \\ V&= \pi (6)^{2} (6) \\ V&= \pi (36)(6) \\ V&= 216 \pi \\ V&= 678.24\text{ in}^{3}\end{aligned}\)
El segundo contenedor tiene 678.24 pulgadas cúbicas.
El contenedor de la izquierda tiene el mayor volumen.
Ejemplo\(\PageIndex{2}\)
Usa la fórmula para encontrar el volumen de un cilindro para responder a la siguiente pregunta.
Un tanque de agua tiene un radio de 50 pies y una altura de 400 pies. ¿Cuántos pies cúbicos de agua aguantará el tanque cuando esté lleno?
Solución
Primero, sustituya la información dada en la fórmula y resuelva.
\(\begin{aligned}V&= \pi r^{2}h \\ V&= \pi (502)(400) \\ V&= \pi (2,500)(400) \\ V&= 1,000,000 \pi \\ V&= 3,140,000\text{ in}^{3}\end{aligned}\)
¡El tanque de agua contendrá más de 3 millones de pies cúbicos de agua!
Ejemplo\(\PageIndex{3}\)
Encuentra el volumen del cilindro.

Solución
Primero, sustituya la información dada en la fórmula y luego resuelva.
\(\begin{aligned}V&= \pi r^{2} h \\ V&= \pi (1^{2})(8) \\ V&= \pi (1)(8) \\ V&= 8 \pi \\ V&= 25.12\text{ in}^{3}\end{aligned}\)
La respuesta es de 25.12 pulgadas cúbicas.
Ejemplo\(\PageIndex{4}\)
Encuentra el volumen del cilindro.
d=10\ texto {ft}\),\(h=12 \text{ ft}\)
Solución
Primero, tenga en cuenta que el diámetro es el doble del radio, así que divida el diámetro por 2 para obtener el radio.
10\ divide 2=5\)
El radio es 5.
A continuación, sustituya la información dada en la fórmula para luego resolver.
\(\begin{aligned}V&= \pi r^{2} h \\ V&= \pi (5)^{2} (12) \\ V&= \pi (25)(12) \\ V&= 300 \pi \\ V&= 942 \text{ ft}^{3}\end{aligned}\)
La respuesta es de 942 pies cúbicos.
Ejemplo\(\PageIndex{5}\)
Encuentra el volumen del cilindro.
\(r=6\text{ in}\),\(h=10\text{ in}\)
Solución
Primero, sustituya la información dada en la fórmula y luego resuelva.
\(\begin{aligned}V&= \pi r^{2} h \\ V&= \pi (6)^{2}(10) \\ V&= \pi (36)(10) \\ V&= 360 \pi \\ V&= 1130.4\text{ in}^{3}\end{aligned}\)
La respuesta es de 1130.4 pulgadas cúbicas.
Revisar
Encuentra el volumen de cada uno de los siguientes cilindros.
- \(r=5\text{ in}\),\(h=8\text{ in}\)
- \(r=4\text{ in}\),\(h=7\text{ in}\)
- \(r=3 \text{ ft}\),\(h=5 \text{ ft}\)
- \(r=3 \text{ ft}\),\(h=8 \text{ ft}\)
- \(r=4 \text{ cm}\),\(h=9 \text{ cm}\)
-

Figura\(\PageIndex{7}\) -

Figura\(\PageIndex{8}\) -

Figura\(\PageIndex{9}\) -
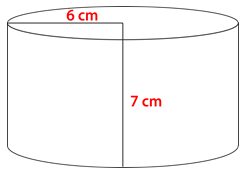
Figura\(\PageIndex{10}\) -
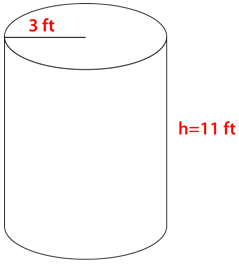
Figura\(\PageIndex{11}\) -

Figura\(\PageIndex{12}\) -

Figura\(\PageIndex{13}\) -

Figura\(\PageIndex{14}\) -
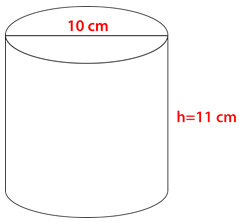
Figura\(\PageIndex{15}\) -

Figura\(\PageIndex{16}\)
El vocabulario
| Término | Definición |
|---|---|
| Cilindro | Un cilindro es una figura sólida con dos bases circulares congruentes paralelas. |
| Radio | El radio de un círculo es la distancia desde el centro del círculo hasta el borde del círculo. |
| Superficie | El área superficial es el área total de todas las superficies de un objeto tridimensional. |
| Volumen | El volumen es la cantidad de espacio dentro de los límites de un objeto tridimensional. |
Recursos adicionales
Elemento Interactivo
Video: Volumen de Geometría Sólida
Práctica: Volumen de Cilindros
Mundo real: ¿Por qué flotan los superpetroleros?

