9.1: Radiación de un Momento Actual

En esta sección, comenzamos a abordar el siguiente problema: Ante una distribución de densidad de corriente impresionada\({\bf J}({\bf r})\), ¿cuál es la intensidad del campo eléctrico resultante\({\bf E}({\bf r})\)? Una ruta hacia una respuesta es a través de las ecuaciones de Maxwell. Viendo las ecuaciones de Maxwell como un sistema de ecuaciones diferenciales, es posible una solución matemática rigurosa dadas las condiciones de límite adecuadas. La solución rigurosa que sigue ese enfoque es relativamente complicada, y se presenta a partir de la Sección 9.2 de este libro.

Si en cambio limitamos el alcance a una distribución de corriente suficientemente simple, es posible una derivación informal simple. En esta sección se presenta dicha derivación. La ventaja de abordar primero un caso especial simple es que nos permitirá evaluar rápidamente la naturaleza de la solución, lo que resultará útil una vez que finalmente abordemos el problema más general. Además, los resultados presentados en esta sección resultarán suficientes para abordar muchas aplicaciones comúnmente encontradas.

Figura\(\PageIndex{1}\): Un momento\(+\hat{\bf{z}}\) de corriente dirigido localizado en el origen. (CC BY-SA 4.0; C. Wang)

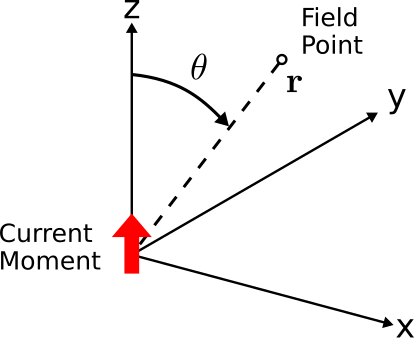
La distribución simple de corriente considerada en esta sección se conoce como momento actual. Un ejemplo de un momento actual se muestra en la Figura\(\PageIndex{1}\) y en este caso se define de la siguiente manera:

\[\Delta{\bf J}({\bf r}) = \hat{\bf z}~I~\Delta l~\delta({\bf r}) \label{m0194_eCM} \]

donde\(I~\Delta l\) es el componente escalar del momento actual, que tiene unidades de longitud de tiempos de corriente (unidades base SI de A\(\cdot\) m); y\(\delta({\bf r})\) es la función de muestreo volumétrico ¹ definida de la siguiente manera:

\ begin {align} ~ &\ delta ({\ bf r})\ triangleq 0~~~\ mbox {para} ~~~ {\ bf r}\ neq 0; ~~~\ mbox {y}\ label {m0194_eDelta1}\ ~ &\ int_ {\ mathcal {V}}\ delta ({\ bf r}) ~dv\ angleq 1\ etiqueta {M0194_Edelta2}\ end {align}

donde\(\mathcal{V}\) está cualquier volumen que incluya el origen (\({\bf r}=0\)). Es evidente a partir de la Ecuación\ ref {M0194_Edelta2} que\(\delta({\bf r})\) tiene unidades base SI de m\(^{-3}\). Posteriormente,\(\Delta{\bf J}({\bf r})\) cuenta con unidades base SI de A/m\(^2\), confirmando que se trata de una densidad de corriente volumétrica. Sin embargo, es la forma más simple posible de densidad de corriente volumétrica, ya que —como indica la Ecuación\ ref {M0194_Edelta1} — existe sólo en el origen y en ningún otro lugar.

Aunque algunas distribuciones actuales se aproximan al momento actual, las distribuciones actuales que se encuentran en la práctica común de ingeniería generalmente no existen precisamente en esta forma. Sin embargo, el momento actual resulta generalmente útil como un “bloque de construcción” a partir del cual se pueden construir distribuciones prácticas de corriente, a través del principio de superposición. La radiación de las distribuciones de corriente construidas de esta manera se calcula simplemente sumando la radiación de cada uno de los momentos de corriente constituyentes.

Ahora consideremos la intensidad del campo eléctrico\(\Delta{\bf E}({\bf r})\) que se crea por esta distribución de corriente. Primero, si la corriente es constante (es decir, “DC”), este problema cae dentro del dominio de la magnetostática; es decir, el resultado es completamente descrito por el campo magnético, y no puede haber radiación. Por lo tanto, limitemos nuestra atención al caso “AC”, para el cual es posible la radiación. Será conveniente emplear representación fasorial. En la representación fasorial, la densidad de corriente es

\[\Delta\widetilde{\bf J}({\bf r}) = \hat{\bf z}~\widetilde{I}~\Delta l~\delta({\bf r}) \label{m0194_eCM2} \]

donde\(\widetilde{I}~\Delta l\) es simplemente el momento actual escalar expresado como un fasor.

Ahora estamos listos para abordar la pregunta “¿A qué se\(\Delta\widetilde{\bf E}({\bf r})\) debe\(\Delta\widetilde{\bf J}({\bf r})\)?” Sin hacer ninguna matemática, sabemos bastante de ello\(\Delta\widetilde{\bf E}({\bf r})\). Por ejemplo:

• Dado que los campos eléctricos son proporcionales a las corrientes que los dan origen, esperamos\(\Delta\widetilde{\bf E}({\bf r})\) ser proporcionales a\(\left|\widetilde{I}~\Delta l\right|\).
• Si estamos lo suficientemente lejos del origen, esperamos\(\Delta\widetilde{\bf E}({\bf r})\) ser aproximadamente proporcionales a\(1/r\) donde\(r\triangleq\left|{\bf r}\right|\) esta la distancia de la corriente de origen. Esto se debe a que las fuentes puntuales dan lugar a ondas esféricas, y la densidad de potencia en una onda esférica sería proporcional a\(1/r^2\). Dado que la densidad de potencia promedio en el tiempo es proporcional a\(\left|\Delta\widetilde{\bf E}({\bf r})\right|^2\),\(\Delta\widetilde{\bf E}({\bf r})\) debe ser proporcional a\(1/r\).
• Si estamos lo suficientemente lejos del origen, y la pérdida debida al medio es insignificante, entonces esperamos que la fase de cambie aproximadamente\(\Delta\widetilde{\bf E}({\bf r})\) a velocidad\(\beta\) donde\(\beta\) está la constante de propagación de fase\(2\pi/\lambda\). Ya que esperamos frentes de fase esféricos, por lo tanto,\(\Delta\widetilde{\bf E}({\bf r})\) deben contener el factor\(e^{-j\beta r}\).
• La ley de Ampere indica que una corriente\(\hat{\bf z}\) -dirigida en el origen debe dar lugar a un campo magnético\(\hat{\bf \phi}\) -dirigido en el\(z=0\) plano. ² Al mismo tiempo, el teorema de Poynting requiere que el producto cruzado de los campos eléctrico y magnético apunte en la dirección del flujo de energía. En el presente problema, esta dirección está alejada de la fuente; es decir,\(+\hat{\bf r}\). Por lo tanto,\(\Delta\widetilde{\bf E}(z=0)\) apunta en la\(-\hat{\bf z}\) dirección. El mismo principio se aplica fuera del\(z=0\) plano, por lo que en general esperamos\(\Delta\widetilde{\bf E}({\bf r})\) apuntar en la\(\hat{\bf \theta}\) dirección.
• Esperamos\(\Delta\widetilde{\bf E}({\bf r})=0\) a lo largo del\(z\) eje. Posteriormente\(\left|\Delta\widetilde{\bf E}(\hat{\bf r})\right|\) deberá aumentar de cero a\(\theta=0\) y volver a cero en\(\theta=\pi\). La simetría del problema sugiere\(\left|\Delta\widetilde{\bf E}(\hat{\bf r})\right|\) es máxima en\(\theta=\pi/2\). Esta magnitud debe variar de la manera más sencilla posible, llevándonos a concluir que\(\Delta\widetilde{\bf E}(\hat{\bf r})\) es proporcional a\(\sin\theta\). Además, la simetría radial del problema significa que no\(\Delta\widetilde{\bf E}(\hat{\bf r})\) debe depender en absoluto de\(\phi\).

Armando estas ideas, concluimos que el campo eléctrico irradiado tiene la siguiente forma:

\[\Delta\widetilde{\bf E}({\bf r}) \approx \hat{\bf \theta} C \left(\widetilde{I}~\Delta l\right) \left(\sin\theta\right) \frac{e^{-j\beta r}}{r} \nonumber \]

donde\(C\) es una constante que da cuenta de todas las constantes de proporcionalidad identificadas en el análisis anterior. Ya que las unidades de\(\Delta\widetilde{\bf E}({\bf r})\) son V/m, las unidades de\(C\) deben ser\(\Omega\) /m. Aún no hemos contabilizado la impedancia de onda del medio\(\eta\), que tiene unidades de\(\Omega\), por lo que sería una buena apuesta basada en las unidades que\(C\) es proporcional a\(\eta\). No obstante, aquí el análisis informal llega a un callejón sin salida, por lo que simplemente vamos a exponer el resultado de la solución rigurosa:\(C=j\eta\beta/4\pi\). Las unidades son correctas, y finalmente obtenemos:

\[\Delta\widetilde{\bf E}({\bf r}) \approx \hat{\bf \theta} \frac{j\eta\beta}{4\pi} \left(\widetilde{I}~\Delta l\right) \left(\sin\theta\right) \frac{e^{-j\beta r}}{r} \nonumber \]

Evidencia adicional de que esta solución es correcta proviene del hecho de que satisface la ecuación de onda\(\nabla^2 \Delta\widetilde{\bf E}({\bf r}) + \beta^2 \Delta\widetilde{\bf E}({\bf r}) = 0\). ³

Obsérvese que la expresión que hemos obtenido para el campo eléctrico radiado es aproximada (de ahí la “\(\approx\)”). Esto se debe en parte a nuestra presunción de una simple onda esférica, que sólo puede ser válida a distancias alejadas de la fuente. Pero, ¿hasta dónde? Una suposición educada serían distancias mucho mayores que una longitud de onda (i.e.,\(r\gg\lambda\)). Esto servirá por ahora; en otra sección, demostraremos rigurosamente que esta conjetura es esencialmente correcta.

Concluimos esta sección señalando que la distribución actual analizada en esta sección a veces es referida como un dipolo hertziano. Un dipolo hertziano se define típicamente como un filamento recto infinitesimalmente delgado de corriente con una longitud que es muy pequeña en relación con una longitud de onda, pero no precisamente cero. Esta interpretación no cambia la solución obtenida en esta sección, por lo que podemos ver el momento actual y el dipolo hertziano como efectivamente los mismos en aplicaciones prácticas de ingeniería.

Lectura adicional:

• “Función delta Dirac” en Wikipedia.
• “Antena dipolo” (sección titulada “Dipolo Hertziano”) en Wikipedia.

---

1. También una forma de la función delta de Dirac; ver “Lectura adicional” al final de esta sección. ↩
2. Esto a veces se describe como la “regla de la mano derecha” de la ley de Ampere. ↩
3. Confirmar esto es sencillo (simplemente sustituir y evaluar) y se deja como un ejercicio para el alumno. ↩