1.2: Números negativos
- Page ID
- 110927
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Los números negativos son una realidad, desde las temperaturas invernales hasta nuestras cuentas bancarias. Practicemos la evaluación de expresiones que involucran números negativos.

Valor Absoluto
El valor absoluto de un número es su distancia de\(0\). Se puede pensar en ello como el tamaño de un número sin identificarlo como positivo o negativo. Los números con el mismo valor absoluto pero signos diferentes, como\(3\) y\(-3\), se denominan opuestos. El valor absoluto de\(-3\) es\(3\), y el valor absoluto de\(3\) es también\(3\).
Utilizamos un par de barras verticales rectas para indicar el valor absoluto; por ejemplo,\(|-3|=3\) y\(|3|=3\).
Evaluar cada expresión.
1. \(|-5|\)
2. \(|5|\)
- Responder
-
1. 5
2. 5
Sumando números negativos
Para sumar dos números negativos, sumar sus valores absolutos (es decir, ignorar los signos negativos) y hacer que la respuesta final sea negativa.
Realizar cada adición.
3. \(-8+(-7)\)
4. \(-13+(-9)\)
- Responder
-
3. -15
4. -22
Para sumar un número positivo y un número negativo, restamos el valor absoluto menor del mayor. Si el número positivo tiene el valor absoluto mayor, la respuesta final es positiva. Si el número negativo tiene el valor absoluto mayor, la respuesta final es negativa.
Realizar cada adición.
5. \(7+(-3)\)
6. \(-7+3\)
7. \(14+(-23)\)
8. \(-14+23\)
9. La temperatura al mediodía de un lunes frío era de\(-7\) °F. Al día siguiente al mediodía, la temperatura había subido\(25\) °F. ¿Cuál era la temperatura al mediodía del martes?
- Responder
-
5. 4
6. -4
7. -9
8. 9
9. \(18\)°F
Si una expresión consiste únicamente en adiciones, podemos romper las reglas para el orden de las operaciones y sumar los números en el orden que escojamos.
Evalúa cada expresión usando cualquier atajo que notes.
10. \(-10+4+(-4)+3+10\)
11. \(-291+73+(-9)+27\)
- Responder
-
10. \(3\)
11. -200
Restar números negativos
La imagen de abajo muestra parte de un talón de pago en el que se necesitaba hacer un\(18\) pago de $, pero la gente de nómina quería rastrear el pago en la categoría de deducciones. Por supuesto, un número positivo en las deducciones restará dinero del cheque de pago. Aquí, sin embargo, una deducción de\(18\) dólares negativos tiene el efecto de agregar\(18\) dólares al cheque de pago. Restar una cantidad negativa equivale a sumar una cantidad positiva.
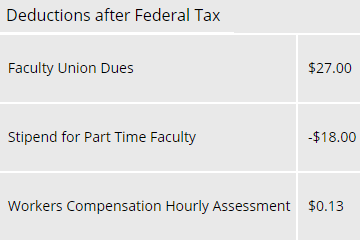
Para restar dos números con signo, sumamos el primer número al opuesto del segundo número.
Realizar cada resta.
12. \(5-2\)
13. \(2-5\)
14. \(-2-5\)
15. \(-5-2\)
16. \(2-(-5)\)
17. \(5-(-2)\)
18. \(-2-(-5)\)
19. \(-5-(-2)\)
20. Un día de febrero, la temperatura en Portland, Oregon es de\(43\) °F, y la temperatura en Portland, Maine, es de\(-12\) °F ¿Cuál es la diferencia de temperatura?
- Responder
-
12. 3
13. -3
14. -7
15. -7
16. 7
17. 7
18. 3
19. -3
20. \(55\)Diferencia de °F
Multiplicar números negativos
Supongamos que gastas\(3\) dólares en un café todos los días. Podríamos representar gastar 3 dólares como número negativo,\(-3\) dólares. En el transcurso de una semana laboral de un\(5\) día, gastarías\(15\) dólares, que podríamos representar como\(-15\) dólares. Esto demuestra que\(-3\cdot5=-15\), o\(5\cdot-3=-15\).

Si se multiplican dos números con signos opuestos, el producto es negativo.
Encuentra cada producto.
21. \(-4\cdot3\)
22. \(5(-8)\)
- Responder
-
21. -12
22. -40
Volviendo a nuestro ejemplo de café, lo vimos\(5(-3)=-15\). Por lo tanto, lo contrario de\(5(-3)\) debe ser positivo\(15\). Porque\(-5\) es lo contrario de\(5\), esto implica eso\(-5(-3)=15\).
Si se multiplican dos números con el mismo signo, el producto es positivo.
¡ADVERTENCIA! Estas reglas son distintas de las reglas de adición; ten cuidado de no mezclarlas.
Encuentra cada producto.
23. \(-2(-9)\)
24. \(-3(-7)\)
- Responder
-
23. 18
24. 21
Recordemos que un exponente representa una multiplicación repetida. Veamos qué pasa cuando elevamos un número negativo a un exponente.
Evaluar cada expresión.
25. \((-2)^2\)
26. \((-2)^3\)
27. \((-2)^4\)
28. \((-2)^5\)
- Responder
-
25. \(4\)
26. -8
27. 16
28. -32
Si un número negativo se eleva a una potencia impar, el resultado es negativo.
Si un número negativo se eleva a una potencia par, el resultado es positivo.
Dividir números negativos
Volvamos al ejemplo del café que vimos antes:\(-3\cdot5=-15\). Podemos reescribir este hecho usando la división y ver eso\(-15\div5=-3\); un negativo dividido por un positivo da un resultado negativo. También,\(-15\div-3=5\); un negativo dividido por un negativo da un resultado positivo. Esto quiere decir que las reglas para la división funcionan exactamente igual que las reglas para la multiplicación.
Si se dividen dos números con signos opuestos, el cociente es negativo.
Si se dividen dos números con el mismo signo, el cociente es positivo.
Encuentra cada cociente.
29. \(-42\div6\)
30. \(32\div(-8)\)
31. \(-27\div(-3)\)
32. \(0\div4\)
33. \(0\div(-4)\)
34. \(4\div0\)
- Responder
-
29. -7
30. -4
31. 9
32. 0
33. 0
34. indefinido
Sigue adelante y revisa esos tres últimos ejercicios con una calculadora. ¿Alguna sorpresa?
- 0 dividido por otro número es 0.
- Un número dividido por 0 no está definido, o no es un número real.
Aquí hay una explicación rápida de por qué no\(4\div0\) puede ser un número real. Supongamos que hay un número misterioso, al que llamaremos\(n\), tal que\(4\div0=n\). Entonces podemos reescribir esta división como una multiplicación relacionada,\(n\cdot0=4\). Pero porque\(0\) veces cualquier número es\(0\), el lado izquierdo de esta ecuación es\(0\), y obtenemos el resultado eso\(0=4\), lo cual no tiene sentido. Por lo tanto, no existe tal número\(n\), y\(4\div0\) no puede ser un número real.
Orden de Operaciones con Números Negativos
P: Trabajar dentro de paréntesis o símbolos de agrupación, siguiendo el orden PEMDAS según sea necesario.
E: Evaluar exponentes.
MD: Realizar multiplicaciones y divisiones de izquierda a derecha.
AS: Realizar adiciones y restas de izquierda a derecha.
Terminemos este módulo con algún orden de práctica de operaciones.
Evaluar cada expresión usando el orden de las operaciones.
35. \((2-5)^2\cdot2+1\)
36. \(2-5^2\cdot(2+1)\)
37. \([7(-2)+16]\div2\)
38. \(7(-2)+16\div2\)
39. \(\dfrac{1-3^4}{2(5)}\)
40. \(\dfrac{(1-3)^4}{2}\cdot5\)
- Responder
-
35. \(19\)
36. -73
37. 1
38. -6
39. -8
40. 40


