5.5: Dividir polinomios
- Page ID
- 112384
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Al final de esta sección, podrás:
- Dividiendo monomios
- Dividir un polinomio por un monomio
- Dividir polinomios usando división larga
- Dividir polinomios usando división sintética
- Dividir funciones polinomiales
- Usar el resto y los teoremas de factores
Antes de comenzar, toma este cuestionario de preparación.
Dividir monomios
Ahora estamos familiarizados con todas las propiedades de los exponentes y las usamos para multiplicar polinomios. A continuación, usaremos estas propiedades para dividir monomios y polinomios.
Encuentra el cociente:\(54a^2b^3÷ (−6ab^5)\).
Solución
Cuando dividimos los monomios con más de una variable, escribimos una fracción para cada variable.
\(\begin{array} {ll} {} &{54a^2b^3÷(−6ab^5)} \\[5pt] {\text{Rewrite as a fraction.}} &{\dfrac{54a^2b^3}{−6ab^5}} \\[5pt] {\text{Use fraction multiplication.}} &{\dfrac{54}{−6}·\dfrac{a^2}{a}·\dfrac{b^3}{b^5}} \\[5pt] {\text{Simplify and use the Quotient Property.}} &{−9·a·\dfrac{1}{b^2}} \\[5pt] {\text{Multiply.}} &{−\dfrac{9a}{b^2}} \end{array}\)
Encuentra el cociente:\(−72a^7b^3÷(8a^{12}b^4)\).
- Contestar
-
\(−\dfrac{9}{a^5b}\)
Encuentra el cociente:\(−63c^8d^3÷(7c^{12}d^2)\).
- Contestar
-
\(\dfrac{−9d}{c^4}\)
Una vez que se familiarice con el proceso y lo haya practicado paso a paso varias veces, es posible que pueda simplificar una fracción en un solo paso.
Encuentra el cociente:\(\dfrac{14x^7y^{12}}{21x^{11}y^6}\).
Solución
Tenga mucho cuidado de simplificar\(\dfrac{14}{21}\) dividiendo un factor común, y de simplificar las variables restando sus exponentes.
\(\begin{array} {ll} {} &{\dfrac{14x^7y^{12}}{21x^{11}y^6}} \\ {\text{Simplify and use the Quotient Property.}} &{\dfrac{2y^6}{3x^4}} \\ \end{array}\)
Encuentra el cociente:\(\dfrac{28x^5y^{14}}{49x^9y^{12}}\).
- Contestar
-
\(\dfrac{4y^2}{7x^4}\)
Encuentra el cociente:\(\dfrac{30m^5n^{11}}{48m^{10}n^{14}}\).
- Contestar
-
\(\dfrac{5}{8m^5n^3}\)
Dividir un polinomio por un monomio
Ahora que sabemos dividir un monomio por un monomio, el siguiente procedimiento es dividir un polinomio de dos o más términos por un monomio. El método que usaremos para dividir un polinomio por un monomio se basa en las propiedades de adición de fracciones. Entonces comenzaremos con un ejemplo para revisar la adición de fracciones. La suma\(\dfrac{y}{5}+\dfrac{2}{5}\) simplifica a\(\dfrac{y+2}{5}\). Ahora haremos esto a la inversa para dividir una sola fracción en fracciones separadas. Por ejemplo,\(\dfrac{y+2}{5}\) se puede escribir\(\dfrac{y}{5}+\dfrac{2}{5}\).
Este es el “reverso” de la adición de fracciones y establece que si a, b y c son números donde\(c\neq 0\), entonces\(\dfrac{a+b}{c}=\dfrac{a}{c}+\dfrac{b}{c}\). Utilizaremos esto para dividir polinomios por monomios.
Para dividir un polinomio por un monomio, dividir cada término del polinomio por el monomio.
Encuentra el cociente:\((18x^3y−36xy^2)÷(−3xy)\).
Solución
\(\begin{array} {ll} {} &{(18x^3y−36xy^2)÷(−3xy)} \\[5pt] {\text{Rewrite as a fraction.}} &{\dfrac{18x^3y−36xy^2}{−3xy}} \\[5pt] {\text{Divide each term by the divisor. Be careful with the signs!}} &{\dfrac{18x^3y}{−3xy}−\dfrac{36xy^2}{−3xy}} \\[5pt] {\text{Simplify.}} &{−6x^2+12y} \end{array}\)
Encuentra el cociente:\((32a^2b−16ab^2)÷(−8ab)\).
- Contestar
-
\(−4a+2b\)
Encuentra el cociente:\((−48a^8b^4−36a^6b^5)÷(−6a^3b^3)\).
- Contestar
-
\(8a^5b+6a^3b^2\)
Dividir polinomios usando división larga
Dividir un polinomio por un binomio, seguimos un procedimiento muy similar a la división larga de números. Entonces, veamos cuidadosamente los pasos que damos cuando dividimos un número de 3 dígitos, 875, por un número de 2 dígitos, 25.
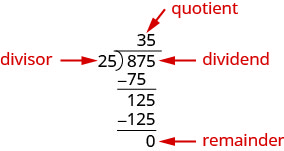
Verificamos la división multiplicando el cociente por el divisor. Si hicimos la división correctamente, el producto debería ser igual al dividendo.
\[\begin{array} {l} {35·25} \\ {875\checkmark} \\ \nonumber \end{array}\]
Ahora vamos a dividir un trinomio por un binomio. Al leer el ejemplo, observe lo similares que son los pasos al ejemplo numérico anterior.
Encuentra el cociente:\((x^2+9x+20)÷(x+5)\).
Solución
| \(\require{enclose}\) | \(\qquad (x^2+9x+20) \div (x+5)\) |
| Escríbelo como un problema de división larga. Asegúrese de que el dividendo esté en forma estándar. |
\(\qquad x+5\enclose{longdiv}{ x^2+9x+20\phantom{0}} \) |
|
Dividir\(x^2\) por\(x\). Puede ser útil preguntarse: “¿Qué necesito |
\(\qquad \begin{array}{r} {\color{red}x}\hspace{2.3em}\\[-3pt] {\color{red}x}+5\enclose{longdiv}{ {\color{red}x^2}+9x+20\phantom{0}} \end{array}\) |
| Poner la respuesta,\(x\), en el cociente sobre el\(x\) término. Multiplicar\(x\) tiempos\(x+5\). Alinee los términos similares bajo el dividendo. |
\(\qquad \begin{array}{r}x\hspace{2.3em}\\[-3pt] x+5\enclose{longdiv}{x^2+9x+20\phantom{0}}\\[-3pt] \underline{\color{red}x^2+5x}\hspace{2.4em} \end{array}\) |
| Restar\(x^2+5x\) de\(x^2+9x\). Puede que le resulte más fácil cambiar las señales y luego agregarlas. Luego derribar el último término,\(20.\) |
\(\qquad \begin{array}{r}x\hspace{2.3em}\\[-3pt] x+5\enclose{longdiv}{x^2+\phantom{00}9x+20\phantom{0}}\\[-3pt] \underline{{\color{red}-}x^2+({\color{red}-}5x)}\hspace{2.1em}\\[-3pt] {\color{red}4x+20}\hspace{0.5em} \end{array}\) |
Dividir\(4x\) por\(x\). Puede ser útil preguntarse: “¿Qué necesito multiplicar\(x\) por para conseguir\(4x\)?” Poner la respuesta,\(4\), en el cociente sobre el término constante. |
\(\qquad \begin{array}{r}x+\phantom{0}{\color{red}4}\hspace{.5em}\\[-3pt] {\color{red}x}+5\enclose{longdiv}{x^2+\phantom{00}9x+20\phantom{0}}\\[-3pt] \underline{{\color{red}-}x^2+({\color{red}-}5x)}\hspace{2.1em}\\[-3pt] {\color{red}4x}+20\hspace{0.5em} \end{array}\) |
| Multiplicar 4 veces\(x+5\). |
\(\qquad \begin{array}{r}x+\phantom{0}4\hspace{.5em}\\[-3pt] x+5\enclose{longdiv}{x^2+\phantom{00}9x+20\phantom{0}}\\[-3pt] \underline{{\color{red}-}x^2+({\color{red}-}5x)}\hspace{2.1em}\\[-3pt] 4x+20\hspace{0.5em}\\[-3pt] \underline{ \color{red}4x+20}\hspace{.5em} \end{array}\) |
| Restar\(4x+20\) de\(4x+20\). |
\(\qquad \begin{array}{r}x+\phantom{0}4\hspace{.5em}\\[-3pt] x+5\enclose{longdiv}{x^2+\phantom{00}9x+20\phantom{0}}\\[-3pt] \underline{{\color{red}-}x^2+({\color{red}-}5x)}\hspace{2.1em}\\[-3pt] 4x+20\hspace{.5em}\\[-3pt] \underline{{\color{red}-}4x+({\color{red}-}20)}\\[-3pt] 0\hspace{.33em}\end{array}\) |
|
Comprobar: \(\begin{array} {ll} {\text{Multiply the quotient by the divisor.}} &{(x+4)(x+5)} \\ {\text{You should get the dividend.}} &{x^2+9x+20\checkmark}\\ \end{array}\) |
Encuentra el cociente:\((y^2+10y+21)÷(y+3)\).
- Contestar
-
\(y+7\)
Encuentra el cociente:\((m^2+9m+20)÷(m+4)\).
- Contestar
-
\(m+5\)
Cuando dividimos 875 por 25, no teníamos resto. Pero a veces la división de números sí deja un resto. Lo mismo ocurre cuando dividimos polinomios. En el siguiente ejemplo, tendremos una división que deja un resto. Escribimos el resto como fracción con el divisor como denominador.
Mira hacia atrás en los dividendos de los ejemplos anteriores. Los términos fueron escritos en orden descendente de grados, y no faltaron grados. El dividendo en este ejemplo será\(x^4−x^2+5x−6\). Le falta un\(x^3\) término. Vamos a añadir en\(0x^3\) como marcador de posición.
Encuentra el cociente:\((x^4−x^2+5x−6)÷(x+2)\).
Solución
Observe que no hay\(x^3\) término en el dividendo. Vamos a añadir\(0x^3\) como marcador de posición.
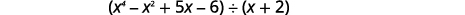 |
|
| Escríbelo como un problema de división larga. Asegúrese de que el dividendo esté en forma estándar con marcadores de posición para términos faltantes. | 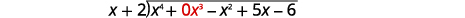 |
| Dividir\(x^4\) por\(x\). Poner la respuesta,\(x^3\), en el cociente sobre el\(x^3\) término. Multiplicar\(x^3\) tiempos\(x+2\). Alinee los términos similares. Restar y luego bajar el siguiente término. |
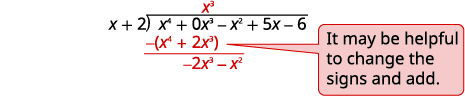 |
| Dividir\(−2x^3\) por\(x\). Poner la respuesta,\(−2x^2\), en el cociente sobre el\(x^2\) término. Multiplicar\(−2x^2\) tiempos\(x+1\). Alinee los términos similares Restar y derribar el siguiente término. |
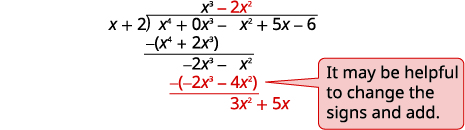 |
| Dividir\(3x^2\) por\(x\). Poner la respuesta,\(3x\), en el cociente sobre el\(x\) término. Multiplicar\(3x\) tiempos\(x+1\). Alinee los términos similares. Restar y derribar el siguiente término. |
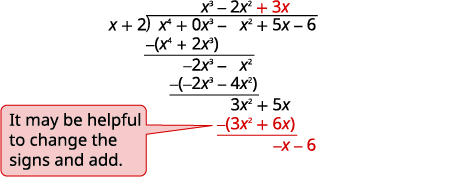 |
| Dividir\(−x\) por\(x\). Poner la respuesta,\(−1\), en el cociente sobre el término constante. Multiplicar\(−1\) tiempos\(x+1\). Alinee los términos similares. Cambia las señales, agrega. Escribe el resto como una fracción con el divisor como denominador. |
 |
| Para verificar, multiplicar\((x+2)(x^3−2x^2+3x−1−4x+2)\). El resultado debe ser\(x^4−x^2+5x−6\). |
Encuentra el cociente:\((x^4−7x^2+7x+6)÷(x+3)\).
- Contestar
-
\(x^3−3x^2+2x+1+3x+3\)
Encuentra el cociente:\((x^4−11x^2−7x−6)÷(x+3)\).
- Contestar
-
\(x^3−3x^2−2x−1−3x+3\)
En el siguiente ejemplo, dividiremos por\(2a−3\). A medida que dividamos, tendremos que considerar tanto las constantes como las variables.
Encuentra el cociente:\((8a^3+27)÷(2a+3)\).
Solución
Esta vez vamos a mostrar la división todo en un solo paso. Necesitamos agregar dos marcadores de posición para poder dividir.
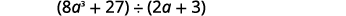 |
|
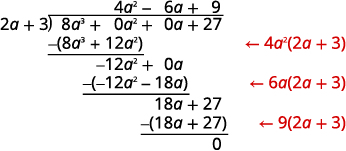 |
Para verificar, multiplicar\((2a+3)(4a^2−6a+9)\).
El resultado debe ser\(8a^3+27\).
Encuentra el cociente:\((x^3−64)÷(x−4)\).
- Contestar
-
\(x^2+4x+16\)
Encuentra el cociente:\((125x^3−8)÷(5x−2)\).
- Contestar
-
\(25x^2+10x+4\)
Dividir polinomios usando división sintética
Como hemos mencionado antes, a los matemáticos les gusta encontrar patrones para facilitar su trabajo. Dado que la división larga puede ser tediosa, echemos un vistazo a la división larga que hicimos en Ejemplo y busquemos algunos patrones. Utilizaremos esto como base para lo que se llama división sintética. A continuación se muestra el mismo problema en el formato de división sintética.
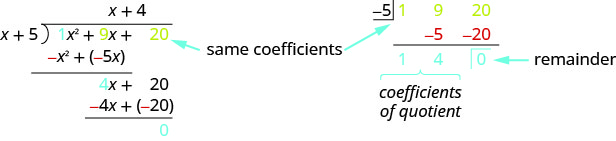
La división sintética básicamente solo elimina variables y números repetidos innecesarios. Aquí\(x^2\) se quitan todos los\(x\) y. Así como los\(−x^2\) y\(−4x\) como son opuestos al término anterior.
- La primera fila de la división sintética son los coeficientes del dividendo. El\(−5\) es lo opuesto al 5 en el divisor.
- La segunda fila de la división sintética son los números que se muestran en rojo en el problema de división.
- La tercera fila de la división sintética son los números mostrados en azul en el problema de división.
Observe que el cociente y el resto se muestran en la tercera fila.
\[\text{Synthetic division only works when the divisor is of the form }x−c. \nonumber \]
En el siguiente ejemplo se explicará el proceso.
Utilice la división sintética para encontrar el cociente y el resto cuando\(2x^3+3x^2+x+8\) se divide por\(x+2\).
Solución
| Escribir el dividendo con poderes decrecientes de\(x\). | 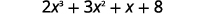 |
| Escribir los coeficientes de los términos como la primera fila de la división sintética. |
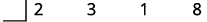 |
| Escriba el divisor como\(x−c\) y coloque c en la división sintética en la caja del divisor. |
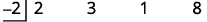 |
| Bajar el primer coeficiente a la tercera fila. | 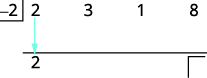 |
| Multiplique ese coeficiente por el divisor y coloque el resultado en la segunda fila debajo del segundo coeficiente. |
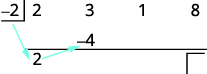 |
| Agrega la segunda columna, poniendo el resultado en la tercera fila. | 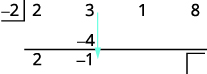 |
| Multiplique ese resultado por el divisor y coloque el resultado en la segunda fila debajo del tercer coeficiente. |
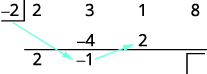 |
| Agrega la tercera columna, poniendo el resultado en la tercera fila. | 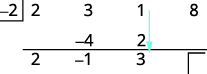 |
| Multiplique ese resultado por el divisor y coloque el resultado en la tercera fila bajo el tercer coeficiente. |
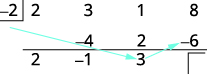 |
| Agrega la columna final, poniendo el resultado en la tercera fila. | 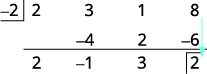 |
| El cociente es\(2x^2−1x+3\) y el resto es 2. |
La división está completa. Los números de la tercera fila nos dan el resultado. Los\(2\space\space\space−1\space\space\space3\) son los coeficientes del cociente. El cociente es\(2x^2−1x+3\). El 2 en la casilla de la tercera fila es el resto.
Comprobar:
\(\begin{align} (\text{quotient})(\text{divisor}) + \text{remainder} &= \text{dividend} \nonumber\\ (2x^2−1x+3)(x+2)+2 &\overset{?}{=} 2x^3+3x^2+x+8 \nonumber\\ 2x^3−x^2+3x+4x^2−2x+6+2 &\overset{?}{=} 2x^3+3x^2+x+8 \nonumber\\ 2x^3+3x^2+x+8 &= 2x^3+3x^2+x+8\checkmark \nonumber \end{align} \)
Utilice la división sintética para encontrar el cociente y el resto cuando\(3x^3+10x^2+6x−2\) se divide por\(x+2\).
- Contestar
-
\(3x^2+4x−2;\space 2\)
Utilice la división sintética para encontrar el cociente y el resto cuando\(4x^3+5x^2−5x+3\) se divide por\(x+2\).
- Contestar
-
\(4x^2−3x+1; 1\)
En el siguiente ejemplo, haremos todos los pasos juntos.
Utilice la división sintética para encontrar el cociente y el resto cuando\(x^4−16x^2+3x+12\) se divide por\(x+4\).
Solución
El polinomio\(x^4−16x^2+3x+12\) tiene su término en orden con grado descendente pero notamos que no hay\(x^3\) término. Añadiremos un 0 como marcador de posición para el\(x^3\) término. En\(x−c\) forma, el divisor es\(x−(−4)\).
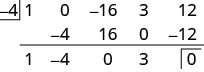
Dividimos un\(4^{\text{th}}\) grado polinomio por un\(1^{\text{st}}\) grado polinomio por lo que el cociente será un\(3^{\text{rd}}\) grado polinomio.
Al leer desde la tercera fila, el cociente tiene los coeficientes\(1\space\space\space−4\space\space\space0\space\space\space3\), que es\(x^3−4x^2+3\). El resto
es 0.
Utilice la división sintética para encontrar el cociente y el resto cuando\(x^4−16x^2+5x+20\) se divide por\(x+4\).
- Contestar
-
\(x^3−4x^2+5;\space 0\)
Utilice la división sintética para encontrar el cociente y el resto cuando\(x^4−9x^2+2x+6\) se divide por\(x+3\).
- Contestar
-
\(x^3−3x^2+2;\space 0\)
Dividir funciones polinomiales
Así como los polinomios se pueden dividir, las funciones polinómicas también se pueden dividir.
Para funciones\(f(x)\) y\(g(x)\), donde\(g(x)\neq 0\),
\[\left(\dfrac{f}{g}\right)(x)=\dfrac{f(x)}{g(x)} \nonumber\]
Para funciones\(f(x)=x^2−5x−14\) y\(g(x)=x+2\), encuentre:
- \(\left(\dfrac{f}{g}\right)(x)\)
- \(\left(\dfrac{f}{g}\right)(−4)\).
Solución
ⓐ
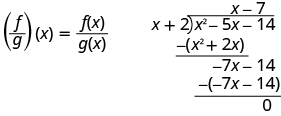
\(\begin{array} {ll} {\text{Substitute for }f(x)\text{ and }g(x).} &{\left(\dfrac{f}{g}\right)(x)=\dfrac{x^2−5x−14}{x+2}} \\[5pt] {\text{Divide the polynomials.}} &{\left(\dfrac{f}{g}\right)(x)=x−7} \end{array} \)
ⓑ En parte ⓐ encontramos\(\left(\dfrac{f}{g}\right)(x)\) y ahora se les pide encontrar\(\left(\dfrac{f}{g}\right)(−4)\).
\(\begin{array} {ll} {} &{\left(\dfrac{f}{g}\right)(x)=x−7} \\[5pt] {\text{To find }\left(\dfrac{f}{g}\right)(−4), \text{ substitute }x=−4.} &{\left(\dfrac{f}{g}\right)(−4)=−4−7} \\[5pt] {} &{\left(\dfrac{f}{g}\right)(−4)=−11} \end{array}\)
Para funciones\(f(x)=x^2−5x−24\) y\(g(x)=x+3\), encuentre:
- \(\left(\dfrac{f}{g}\right)(x)\)
- \(\left(\dfrac{f}{g}\right)(−3)\).
- Contestar a
-
\(\left(\dfrac{f}{g}\right)(x)=x−8\)
- Respuesta b
-
\(\left(\dfrac{f}{g}\right)(−3)=−11\)
Para funciones\(f(x)=x2−5x−36\) y\(g(x)=x+4\), encuentre:
- \(\left(\dfrac{f}{g}\right)(x)\)
- \(\left(\dfrac{f}{g}\right)(−5)\).
- Contestar a
-
\(\left(\dfrac{f}{g}\right)(x)=x−9\)
- Respuesta b
-
\(\left(\dfrac{f}{g}\right)(x)=x−9\)
Usar el teorema del resto y del factor
Veamos los problemas de división que acabamos de trabajar que terminaron con un resto. Se resumen en la siguiente tabla. Si tomamos el dividendo de cada problema de división y lo usamos para definir una función, obtenemos las funciones que se muestran en el gráfico. Cuando el divisor se escribe como\(x−c\), el valor de la función at\(c\),\(f(c)\), es el mismo que el resto del problema de división.
| Dividendo | Divisor\(x−c\) | Resto | Función | \(f(c)\) |
|---|---|---|---|---|
| \(x^4−x^2+5x−6\) | \ (x−c\)” datos-valign="top">\(x−(−2)\) | \(−4\) | \(f(x)=x^4−x^2+5x−6\) | \ (f (c)\)” datos-valign="top">\(−4\) |
| \(3x^3−2x^2−10x+8\) | \ (x−c\)” datos-valign="top">\(x−2\) | 4 | \(f(x)=3x^3−2x^2−10x+8\) | \ (f (c)\)” datos-valign="top">4 |
| \(x^4−16x^2+3x+15\) | \ (x−c\)” datos-valign="top">\(x−(−4)\) | 3 | \(f(x)=x^4−16x^2+3x+15\) | \ (f (c)\)” datos-valign="top">3 |
Para ver esto de manera más general, nos damos cuenta de que podemos verificar un problema de división multiplicando el cociente por el divisor y sumando el resto. En notación de funciones podríamos decir, para obtener el dividendo\(f(x)\), multiplicamos el cociente,\(q(x)\) multiplicamos el divisor,\(x−c\), y sumamos el resto,\(r\).
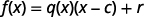 |
|
| Si evaluamos esto en\(c\), obtenemos: | 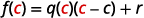 |
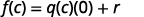 |
|
 |
Esto nos lleva al Teorema del Resto.
Si la función polinómica\(f(x)\) está dividida por\(x−c\), entonces el resto es\(f(c)\).
Usa el Teorema del Resto para encontrar el resto cuando\(f(x)=x^3+3x+19\) se divide por\(x+2\).
Solución
Para usar el Teorema del Resto, debemos usar el divisor en la\(x−c\) forma. Podemos escribir el divisor\(x+2\) como\(x−(−2)\). Entonces, nuestro\(c\) es\(−2\).
Para encontrar el resto, evaluamos\(f(c)\) cual es\(f(−2)\).
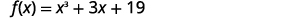 |
|
| Evaluar\(f(−2)\), sustituir\(x=−2\). | 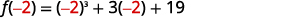 |
| Simplificar. | 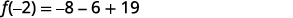 |
 |
|
| El resto es 5 cuando\(f(x)=x^3+3x+19\) se divide por\(x+2\). | |
| Comprobar: Use división sintética para verificar. |
|
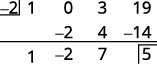 |
|
| El resto es 5. |
Usa el Teorema del Resto para encontrar el resto cuando\(f(x)=x^3+4x+15\) se divide por\(x+2\).
- Contestar
-
\(−1\)
Usa el Teorema del Resto para encontrar el resto cuando\(f(x)=x^3−7x+12\) se divide por\(x+3\).
- Contestar
-
\(6\)
Cuando dividimos\(8a^3+27\) por\(2a+3\) en Ejemplo el resultado fue\(4a^2−6a+9\). Para revisar nuestro trabajo, multiplicamos\(4a2−6a+9\) por\(2a+3\) para conseguir\(8a^3+27\).
\[(4a^2−6a+9)(2a+3)=8a^3+27 \nonumber \]
Escrito de esta manera, podemos ver eso\(4a^2−6a+9\) y\(2a+3\) son factores de\(8a^3+27\). Cuando hicimos la división, el resto era cero.
Siempre que un divisor\(x−c\),, divide una función polinómica,\(f(x)\), y dando como resultado un resto de cero, decimos que\(x−c\) es un factor de\(f(x)\).
Lo contrario también es cierto. Si\(x−c\) es un factor de\(f(x)\) entonces\(x−c\) dividirá la función polinómica resultando en un resto de cero.
Esto lo expondremos en el Teorema de los Factores.
Para cualquier función polinómica\(f(x)\),
- si\(x−c\) es un factor de\(f(x)\), entonces\(f(c)=0\)
- si\(f(c)=0\), entonces\(x−c\) es un factor de\(f(x)\)
Utilice el Teorema del Resto para determinar si\(x−4\) es un factor de\(f(x)=x^3−64\).
Solución
El Teorema del Factor nos dice que\(x−4\) es un factor de\(f(x)=x^3−64\) si\(f(4)=0\).
\(\begin{array} {ll} {} &{f(x)=x^3−64} \\[5pt] {\text{To evaluate }f(4) \text{ substitute } x=4.} &{f(4)=4^3−64} \\[5pt] {\text{Simplify.}} &{f(4)=64−64} \\[5pt]{\text{Subtract.}} &{f(4)=0} \end{array}\)
Ya que\(f(4)=0, x−4\) es un factor de\(f(x)=x^3−64\).
Utilice el Teorema de Factores para determinar si\(x−5\) es un factor de\(f(x)=x^3−125\).
- Contestar
-
si
Utilice el Teorema de Factores para determinar si\(x−6\) es un factor de\(f(x)=x^3−216\).
- Contestar
-
si
Acceda a estos recursos en línea para obtener instrucción adicional y práctica con polinomios divididos.
- Dividir un polinomio por un binomio
- Teorema de División Sintética y Resto
Conceptos clave
- División de un polinomio por un monomio
- Para dividir un polinomio por un monomio, dividir cada término del polinomio por el monomio.
- División de Funciones Polinómicas
- Para funciones\(f(x)\) y\(g(x)\), donde\(g(x)\neq 0\),
\(\left(\dfrac{f}{g}\right)(x)=\dfrac{f(x)}{g(x)}\)
- Para funciones\(f(x)\) y\(g(x)\), donde\(g(x)\neq 0\),
- Teorema del resto
- Si la función polinómica\(f(x)\) está dividida por\(x−c\), entonces el resto es\(f(c)\).
- Teorema del Factor: Para cualquier función polinómica\(f(x)\),
- si\(x−c\) es un factor de\(f(x)\), entonces\(f(c)=0\)
- si\(f(c)=0\), entonces\(x−c\) es un factor de\(f(x)\)


