1.9: Los números reales
- Page ID
- 110445
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Al final de esta sección, podrás:
- Simplifica expresiones con raíces cuadradas
- Identificar números enteros, números racionales, números irracionales y números reales
- Localizar fracciones en la recta numérica
- Localizar decimales en la recta numérica
Una introducción más completa a los temas tratados en esta sección se puede encontrar en los capítulos de Preálgebra, Decimales y Propiedades de los Números Reales.
Simplifique las expresiones con raíces cuadradas
Recuerda que cuando un número\(n\) se multiplica por sí mismo, lo escribimos\(n^{2}\) y leemos “\(n\)al cuadrado”. El resultado se llama el cuadrado de\(n\). Por ejemplo,
\[\begin{array} { l l } { 8 ^ { 2 } } & { \text { read '8 squared' } } \\ { 64 } & { 64 \text { is called the square of } 8 \text { . } } \end{array}\]
De igual manera, 121 es el cuadrado de 11, porque\(11^{2}\) es 121.
Si\(n^{2}=m\), entonces\(m\) es el cuadrado de\(n\).
Hacer la actividad de Matemáticas Manipulativas “Números Cuadrados” te ayudará a desarrollar una mejor comprensión de los números cuadrados perfectos.
Completa la siguiente tabla para mostrar los cuadrados de los números de conteo del 1 al 15.

Los números de la segunda fila se denominan números cuadrados perfectos. Será útil aprender a reconocer los números cuadrados perfectos.
Los cuadrados de los números de conteo son números positivos. ¿Y los cuadrados de los números negativos? Sabemos que cuando los signos de dos números son iguales, su producto es positivo. Por lo que el cuadrado de cualquier número negativo también es positivo.
\[( - 3 ) ^ { 2 } = 9 \quad ( - 8 ) ^ { 2 } = 64 \quad ( - 11 ) ^ { 2 } = 121 \quad ( - 15 ) ^ { 2 } = 225\]
¿Se dio cuenta de que estos cuadrados son los mismos que los cuadrados de los números positivos?
A veces tendremos que mirar a la inversa la relación entre los números y sus cuadrados. Porque\(10^{2}=100\), decimos 100 es el cuadrado de 10. También decimos que 10 es una raíz cuadrada de 100. Un número cuyo cuadrado es mm se llama raíz cuadrada de\(m\).
Si\(n^{2}=m\), entonces\(n\) es una raíz cuadrada de\(m\).
Observe\((−10)^{2}=100\) también, por lo que también\(−10\) es una raíz cuadrada de\(100\). Por lo tanto, ambos\(10\) y\(−10\) son raíces cuadradas de\(100\).
Entonces, cada número positivo tiene dos raíces cuadradas, una positiva y otra negativa. ¿Y si solo quisiéramos la raíz cuadrada positiva de un número positivo? El signo radical,\(\sqrt{m}\), denota la raíz cuadrada positiva. La raíz cuadrada positiva se llama raíz cuadrada principal. Cuando usamos el signo radical eso siempre significa que queremos la raíz cuadrada principal.
También utilizamos el signo radical para la raíz cuadrada de cero. Porque\(0^{2}=0, \sqrt{0}=0\). Observe que cero tiene solo una raíz cuadrada.
\(\sqrt{m}\)se lee “la raíz cuadrada de\(m\)”
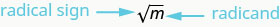
Si\(m = n^{2}\), entonces\(\sqrt{m} = n\), para\(n\geq 0\).
La raíz cuadrada de\(m\),\(\sqrt{m}\), es el número positivo cuyo cuadrado es\(m\).
Ya que 10 es la raíz cuadrada principal de 100, escribimos\(\sqrt{100}=10\). Es posible que desee completar la siguiente tabla para ayudarle a reconocer las raíces cuadradas.

Simplificar:
- \(\sqrt{25}\)
- \(\sqrt{121}\)
- Responder
-
- \[\begin{array} {ll} {} &{\sqrt{25}} \\ {\text {Since }5^{2} = 25} &{5} \end{array}\]
- \[\begin{array} {ll} {} &{\sqrt{121}} \\ {\text {Since }11^{2} = 121} &{11} \end{array}\]
Simplificar:
- \(\sqrt{36}\)
- \(\sqrt{169}\)
- Responder
-
- 6
- 13
Simplificar:
- \(\sqrt{16}\)
- \(\sqrt{196}\)
- Responder
-
- 4
- 14
Sabemos que cada número positivo tiene dos raíces cuadradas y el signo radical indica el positivo. Escribimos\(\sqrt{100)=10\). Si queremos encontrar la raíz cuadrada negativa de un número, colocamos un negativo frente al signo radical. Por ejemplo,\(-\sqrt{100)=-10\). Leemos\(-\sqrt{100)\) como “lo contrario de la raíz cuadrada de 10”.
Simplificar:
- \(-\sqrt{9}\)
- \(-\sqrt{144}\)
- Responder
-
- \[\begin{array} {ll} {} &{-\sqrt{9}} \\ {\text {The negative is in front of the radical sign.}} &{-3} \end{array}\]
- \[\begin{array} {ll} {} &{-\sqrt{144}} \\ {\text {The negative is in front of the radical sign.}} &{-12} \end{array}\]
Simplificar:
- \(\sqrt{16}\)
- \(\sqrt{196}\)
- Responder
-
- −2
- −15
Simplificar:
- \(\sqrt{16}\)
- \(\sqrt{196}\)
- Responder
-
- −9
- −10
Identificar números enteros, números racionales, números irracionales y números reales
Ya hemos descrito los números como números de conteo s, números enteros y enteros. ¿Cuál es la diferencia entre estos tipos de números?
\[\begin{array} { l l } { \text { Counting numbers } } & { 1,2,3,4 , \ldots } \\ { \text { Whole numbers } } & { 0,1,2,3,4 , \ldots } \\ { \text { Integers } } & { \dots - 3 , - 2 , - 1,0,1,2,3 , \ldots } \end{array}\]
¿Qué tipo de números obtendríamos si empezáramos con todos los enteros y luego incluimos todas las fracciones? Los números que tendríamos forman el conjunto de números racionales. Un número racional es un número que se puede escribir como una relación de dos enteros.
Un número racional es un número de la forma\(\dfrac{p}{q}\), donde p y q son números enteros y\(q \neq 0\)
Un número racional se puede escribir como la relación de dos enteros.
Todas las fracciones firmadas, como\(\dfrac{4}{5}\),\(-\dfrac{7}{8}\),\(\dfrac{13}{4}\),\(-\dfrac{20}{3}\) son números racionales. Cada numerador y cada denominador es un entero.
¿Los números enteros son racionales? Para decidir si un entero es un número racional, intentamos escribirlo como una relación de dos enteros. Cada entero se puede escribir como una relación de números enteros de muchas maneras. Por ejemplo, 3 equivale a\(\dfrac{3}{1}\)\(-\dfrac{6}{2}\),\(\dfrac{9}{3}\),\(\dfrac{12}{4}\),\(-\dfrac{15}{5} \ldots\)
Una manera fácil de escribir un entero como una relación de enteros es escribirlo como una fracción con denominador uno.
\[3 = \frac { 3 } { 1 } \quad - 8 = - \frac { 8 } { 1 } \quad 0 = \frac { 0 } { 1 }\]
Como cualquier entero puede escribirse como la relación de dos enteros, ¡todos los enteros son números racionales! Recuerden que los números de conteo y los números enteros también son enteros, y así ellos, también, son racionales.
¿Qué pasa con los decimales? ¿Son racionales? Veamos algunos para ver si podemos escribir cada uno de ellos como la proporción de dos enteros.
Ya hemos visto que los enteros son números racionales. El entero\(−8\) podría escribirse como el decimal\(−8.0\). Entonces, claramente, algunos decimales son racionales.
Piensa en el decimal\(7.3\). ¿Podemos escribirlo como una relación de dos enteros? Porque\(7.3\) significa\(7\dfrac{3}{10}\), podemos escribirlo como una fracción impropia,\(\dfrac{73}{10}\). Así\(7.3\) es la relación de los enteros\(73\) y\(10\). Es un número racional.
En general, cualquier decimal que termine después de un número de dígitos (como\(7.3\) o\(−1.2684\)) es un número racional. Podemos usar el valor posicional del último dígito como denominador al escribir el decimal como fracción.
Escribe como la relación de dos enteros:
- −27
- 7.31
- Responder
-
- \[\begin{array} {ll} {} &{-27} \\ {\text {Write it as a fraction with denominator 1.}} &{\dfrac{-27}{1}} \end{array}\]
- \[\begin{array} {ll} {} &{7.31} \\ {\text {Write is as a mixed number. Remember.}} &{} \\ {\text {7 is the whole number and the decimal}} &{7\dfrac{31}{100}} \\ {\text {part, 0.31, indicates hundredths.}} &{} \\ {\text{Convert to an improper fraction.}} &{\dfrac{731}{100}} \end{array}\]
Entonces vemos que −27 y 7.31 son ambos números racionales, ya que pueden escribirse como la proporción de dos enteros.
Escribe como la relación de dos enteros:
- −24
- 3.57
- Responder
-
- \(\dfrac{-24}{1}\)
- \(\dfrac{357}{100}\)
Escribe como la relación de dos enteros:
- −19
- 8.41
- Responder
-
- \(\dfrac{-19}{1}\)
- \(\dfrac{841}{100}\)
Hemos visto que cada entero es un número racional, ya que\(a = \dfrac{a}{1}\) para cualquier entero,\(a\). También podemos cambiar cualquier entero a un decimal añadiendo un punto decimal y un cero.
\[\begin{array} { l l l l l l l } { \text { Integer } } & { - 2 } & { - 1 } & { 0 } & { 1 } & { 2 } & { 3 } \\ { \text { Decimal form } } & { - 2.0 } & { - 1.0 } & { 0.0 } & { 1.0 } & { 2.0 } & { 3.0 } \\ { } & { \text { These decimal numbers stop. } } \end{array}\]
También hemos visto que cada fracción es un número racional. Mira la forma decimal de las fracciones que consideramos anteriormente.
\[\begin{array} { l l l l } { \text { Ratio of integers } } & { \frac { 4 } { 5 } } & { - \frac { 7 } { 8 } } & { \frac { 13 } { 4 } } & { - \frac { 20 } { 3 } } \\ { \text { The decimal form } } & { 0.8 } & { - 0.875 } & { 3.25 } & { - 6.666 \dots } \\ { } & { } & { } & { - 6.\overline{6} } \\ { } & { \text { These decimal either stop or repeat. } } \end{array}\]
¿Qué nos dicen estos ejemplos?
Cada número racional se puede escribir tanto como una relación de enteros, (\(\dfrac{p}{q}\), donde p y q son enteros y\(q\neq 0\)), y como un decimal que se detiene o se repite.
Aquí están los números que miramos anteriormente expresados como una relación de enteros y como decimal:
| Fracciones | Enteros | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Número | \(\frac{4}{5}\) | \(\frac{7}{8}\) | \(\frac{13}{4}\) | \(-\frac{20}{3}\) | −2 | −1 | 0 | 1 | 2 | 3 |
| Relación de números enteros | \(\frac{4}{5}\) | \(\frac{7}{8}\) | \(\frac{13}{4}\) | \(-\frac{20}{3}\) | \(-\frac{2}{1}\) | \(-\frac{1}{1}\) | \(\frac{0}{1}\) | \(\frac{1}{1}\) | \(\frac{2}{1}\) | \(\frac{3}{1}\) |
| Forma Decimal | 0.8 | −0.875 | 3.25 | \(−6.\overline{6}\) | −2.0 | −1.0 | 0.0 | 1.0 | 2.0 | 3.0 |
Un número racional es un número de la forma\(\frac{p}{q}\), donde p y q son números enteros y\(q\neq 0\)
Su forma decimal se detiene o se repite.
¿Hay decimales que no se detienen ni repiten? ¡Sí!
El número\(\pi\) (la letra griega pi, pronunciada “pie”), que es muy importante para describir los círculos, tiene una forma decimal que no se detiene ni se repite.
\[\pi =3.141592654\ldots\]
Incluso podemos crear un patrón decimal que no se detenga ni repita, como
\[2.01001000100001\ldots\]
Los números cuya forma decimal no se detiene ni se repite no pueden escribirse como una fracción de enteros. A estos números los llamamos irracionales.
Un número irracional es un número que no se puede escribir como la relación de dos enteros.
Su forma decimal no se detiene y no se repite.
Resumimos un método que podemos usar para determinar si un número es racional o irracional.
Si la forma decimal de un número
- repite o detiene, el número es racional.
- no repite y no se detiene, el número es irracional.
Teniendo en cuenta la\(0.58\overline{3}, 0.47, 3.605551275\ldots\) lista de números
- números racionales
- números irracionales.
- Responder
-
- \[\begin{array} {ll} {\text{Look for decimals that repeat or stop}} &{\text{The 3 repeats in }0.58\overline{3}.} \\ {} &{\text {The decimal 0.47 stops after the 7.}}\\ {} &{\text {So } 0.58\overline{3} \text{ and } 0.47 \text{are rational}} \end{array}\]
- \[\begin{array} {ll} {\text{Look for decimals that repeat or stop}} &{3.605551275\ldots\text{has no repeating block of}} \\ {} &{\text {digits and it does not stop.}}\\ {} &{\text {So } 3.605551275\ldots \text{ is irrational.}} \end{array}\]
Para los números dados, enumere el
- números racionales
- números irracionales:\(0.29, 0.81\overline{6}, 2.515115111….\)
- Responder
-
- \(0.29, 0.81\overline{6}\)
- \(2.515115111….\)
Para los números dados, enumere el
- números racionales
- números irracionales:\(2.6\overline{3}, 0.125, 0.418302…\)
- Responder
-
- \(2.6\overline{3}, 0.125\)
- \(0.418302…\)
Por cada número dado, identificar si es racional o irracional:
- \(\sqrt{36}\)
- \(\sqrt{44}\)
- Responder
-
- Reconocer que 36 es un cuadrado perfecto, ya que\(6^{2} = 36\). Entonces\(\sqrt{36} = 6\), por lo tanto,\(\sqrt{36}\) es racional.
- Recuerda eso\(6^{2} = 36\) y\(7^{2} = 49\), así no\(44\) es un cuadrado perfecto. Por lo tanto, la forma decimal de nunca\(\sqrt{44}\) se repetirá y nunca se detendrá, así\(\sqrt{44}\) es irracional.
Por cada número dado, identificar si es racional o irracional:
- \(\sqrt{81}\)
- \(\sqrt{17}\)
- Responder
-
- racional
- irracional
Por cada número dado, identificar si es racional o irracional:
- \(\sqrt{116}\)
- \(\sqrt{121}\)
- Responder
-
- irracional
- racional
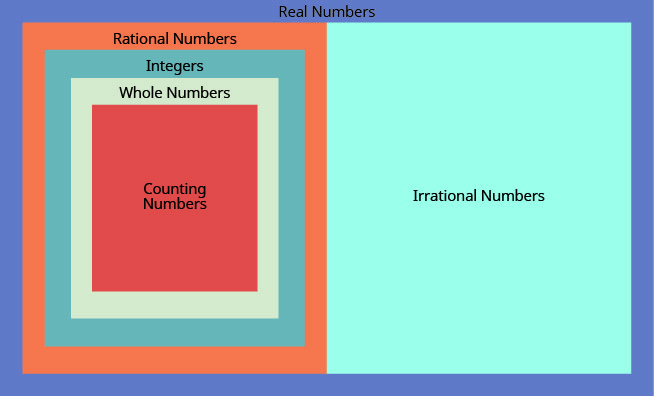
Hemos visto que todos los números de conteo son números enteros, todos los números enteros son números enteros, y todos los enteros son números racionales. Los números irracionales son números cuya forma decimal no se detiene y no se repite. Cuando armamos los números racionales y los números irracionales, obtenemos el conjunto de números reales s.
Un número real es un número que es racional o irracional.
Todos los números que usamos en álgebra elemental son números reales. La figura\(\PageIndex{3}\) ilustra cómo encajan los conjuntos de números que hemos discutido en esta sección.
¿Podemos simplificar\(\sqrt{-25}\)? ¿Hay un número cuyo cuadrado es\(−25\)?
\[(\quad)^{2}=−25?\]
Ninguno de los números que hemos tratado hasta ahora tiene un cuadrado que sea\(−25\). ¿Por qué? Cualquier número positivo al cuadrado es positivo. Cualquier número negativo al cuadrado es positivo. Entonces decimos que no hay un número real igual a\(\sqrt{-25}\).
La raíz cuadrada de un número negativo no es un número real.
Por cada número dado, identifique si es un número real o no un número real:
- \(\sqrt{-169}\)
- \(-\sqrt{64}\)
- Responder
-
- No hay un número real cuyo cuadrado sea\(−169\). Por lo tanto, no\(\sqrt{-169}\) es un número real.
- Ya que lo negativo está frente al radical,\(-\sqrt{64}\) es\(−8\), ya que\(−8\) es un número real,\(-\sqrt{64}\) es un número real.
Por cada número dado, identifique si es un número real o no un número real:
- \(\sqrt{-196}\)
- \(-\sqrt{81}\)
- Responder
-
- no es un número real
- número real
Por cada número dado, identifique si es un número real o no un número real:
- \(-\sqrt{49}\)
- \(\sqrt{-121}\)
- Responder
-
- número real
- no es un número real
Dados los números\(−7, \frac{14}{5}, 8, \sqrt{5}, 5.9, \sqrt{64}\), enumere el
- números enteros
- enteros
- números racionales
- números irracionales
- números reales
- Responder
-
- Recuerda, los números enteros son 0, 1, 2, 3,... y 8 es el único número entero dado.
- Los enteros son los números enteros, sus opuestos y 0. Así que el número entero 8 es un número entero, y −7 es lo opuesto a un número entero así que también es un número entero. También, fíjese que 64 es el cuadrado de 8 así\(-\sqrt{64} = -8\). Entonces los enteros son\(−7, 8, \sqrt{64}\).
- Como todos los enteros son racionales, entonces\(-7, 8, -\sqrt{64}\) son racionales. Los números racionales también incluyen fracciones y decimales que se repiten o se detienen, así\(\frac{14}{5}\) y\(5.9\) son racionales. Entonces la lista de números racionales es\(−7, \frac{14}{5}, 8, 5.9, \sqrt{64}\)
- Recuerda que 5 no es un cuadrado perfecto, por lo que\(\sqrt{5}\) es irracional.
- Todos los números listados son números reales.
Para los números dados, enumere el
- números enteros
- enteros
- números racionales
- números irracionales
- números reales:\(−3, -\sqrt{2}, 0.\overline{3}, \frac{9}{5}, 4, \sqrt{49}\)
- Responder
-
- \(4, \sqrt{49}\).
- \(−3, 4, \sqrt{49}\)
- \(−3, 0.\overline{3}, \frac{9}{5}, 4, \sqrt{49}\)
- \( -\sqrt{2}\)
- \(−3, \sqrt{2}, 0.\overline{3}, \frac{9}{5}, 4, \sqrt{49}\)
Para los números dados, enumere el
- números enteros
- enteros
- números racionales
- números irracionales
- números reales:\(−\sqrt{25},−\frac{3}{8}, −1, 6, \sqrt{121}, 2.041975…\)
- Responder
-
- \(6, \sqrt{121}\).
- \(−\sqrt{25}, −1, 6, \sqrt{121}\)
- \(−\sqrt{25},−\frac{3}{8}, −1, 6, \sqrt{121}\)
- \(2.041975…\)
- \(−\sqrt{25},−\frac{3}{8}, −1, 6, \sqrt{121}, 2.041975…\)
Localizar fracciones en la línea numérica
La última vez que miramos la recta numérica, solo tenía enteros positivos y negativos en ella. Ahora queremos incluir fracciones s y decimales en él.
Hacer la actividad de Matemáticas Manipulativas “Línea numérica Parte 3” te ayudará a desarrollar una mejor comprensión de la ubicación de las fracciones en la recta numérica.
Empecemos con fracciones y localicemos\(\frac{1}{5}, -\frac{4}{5}, 3, \frac{7}{4}, -\frac{9}{2}, -5\) y\(\frac{8}{3}\) en la recta numérica.
Empezaremos con los números enteros 3 y −5. porque son los más fáciles de trazar. Ver Figura\(\PageIndex{4}\).
Las fracciones propias listadas son\(\frac{1}{5}\text{ and } -\frac{4}{5}\). Sabemos que la fracción propiamente dicha\(\frac{1}{5}\) tiene un valor menor a uno y así se ubicaría entre 0 y 1. El denominador es 5, por lo que dividimos la unidad de 0 a 1 en 5 partes iguales\(\frac{1}{5}, \frac{2}{5}, \frac{3}{5}, \frac{4}{5}\). Trazar\(\frac{1}{5}\). Ver Figura\(\PageIndex{4}\).
Del mismo modo,\(-\frac{4}{5}\) está entre 0 y −1. Después de dividir la unidad en 5 partes iguales trazamos\(-\frac{4}{5}\). Ver Figura\(\PageIndex{4}\).
Por último, mira las fracciones impropias\(\frac{7}{4}, -\frac{9}{2}, \frac{8}{3}\). Se trata de fracciones en las que el numerador es mayor que el denominador. Localizar estos puntos puede ser más fácil si cambias cada uno de ellos a un número mixto. Ver Figura\(\PageIndex{4}\).
\[\frac { 7 } { 4 } = 1 \frac { 3 } { 4 } \quad - \frac { 9 } { 2 } = - 4 \frac { 1 } { 2 } \quad \frac { 8 } { 3 } = 2 \frac { 2 } { 3 }\]La figura\(\PageIndex{4}\) muestra la recta numérica con todos los puntos trazados.

Localice y etiquete lo siguiente en una recta numérica:\(4, \frac{3}{4}, -\frac{1}{4}, -3, \frac{6}{5}, -\frac{5}{2}\) y\(\frac{7}{3}\).
- Responder
-
Localizar y trazar los enteros, 4, −3.
Localice\(\frac{3}{4}\) primero la fracción adecuada. La fracción\(\frac{3}{4}\) está entre 0 y 1. Dividimos la distancia entre 0 y 1 en cuatro partes iguales luego, trazamos\(\frac{3}{4}\). Del mismo modo parcela\(-\frac{1}{4}\).
Ahora localice las fracciones impropias\(\frac{6}{5}\),\(-\frac{5}{2}\),\(\frac{7}{3}\). Es más fácil trazarlos si los convertimos a números mixtos y luego los trazamos como se describió anteriormente:\(\frac{6}{5} = 1\frac{1}{5}\),\(-\frac{5}{2} = -2\frac{1}{2}\),\(\frac{7}{3} = 2\frac{1}{3}\).

Localice y etiquete lo siguiente en una recta numérica:\(-1, \frac{1}{3}, \frac{6}{5}, -\frac{7}{4}, \frac{9}{2}, 5\) y\(-\frac{8}{3}\).
- Responder
-
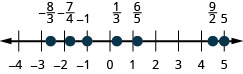
Localice y etiquete lo siguiente en una recta numérica:\(\frac{1}{5}, -\frac{4}{5}, 3, \frac{7}{4}, -\frac{9}{2}, -5\) y\(\frac{8}{3}\).
- Responder
-
En Ejercicio\(\PageIndex{25}\), usaremos los símbolos de desigualdad para ordenar fracciones. En capítulos anteriores se utilizó la línea numérica para ordenar números.
- \(a < b\)“a es menor que b” cuando a está a la izquierda de b en la recta numérica
- \(a > b\)“a es mayor que b” cuando a está a la derecha de b en la recta numérica
A medida que nos movemos de izquierda a derecha en una recta numérica, los valores aumentan.
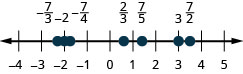
Ordene cada uno de los siguientes pares de números, usando\(<\) o\(>\). Puede ser útil hacer referencia a la Figura\(\PageIndex{5}\).
- \(−\frac{2}{3}\text{___}-1\)
- \(−3\frac{1}{2}\text{___}-3\)
- \(−\frac{3}{4}\text{___}-\frac{1}{4}\)
- \(−2\text{___}-\frac{8}{3}\)

- Responder
-
Tenga cuidado al ordenar números negativos.
- \(\begin{array} { r r } { } & { - \frac { 2 } { 3 } \text{ ___ } -1 } \\ { - \frac { 2 } { 3 } \text { is to the right of } - 1 \text { on the number line. } } & { - \frac { 2 } { 3 } > - 1 } \end{array}\)
- \(\begin{array} { r r } { } & { - 3\frac { 1 } { 2 } \text{ ___ } -3 } \\ { - 3\frac { 1 } { 2 } \text { is to the right of } - 3 \text { on the number line. } } & { - \frac { 2 } { 3 } > - 1 } \end{array}\)
- \(\begin{array} { r r } { } & { - \frac { 3 } { 4 } \text{ ___ } -\frac{1}{4} } \\ { - \frac { 3 } { 4 } \text { is to the right of } - \frac{1}{4} \text { on the number line. } } & { - \frac{3}{4} < - \frac{1}{4} } \end{array}\)
- \(\begin{array} { r r } { } & { - \-2 \text{ ___ } -\frac{8}{3} } \\ { -2 \text { is to the right of } - \frac{8}{3} \text { on the number line. } } & { -2 > -\frac{8}{3} } \end{array}\)
Ordene cada uno de los siguientes pares de números, usando\(<\) o\(>\).
- \(−\frac{1}{3}\text{___}-1\)
- \(−1\frac{1}{2}\text{___}-2\)
- \(−\frac{2}{3}\text{___}-\frac{1}{3}\)
- \(−3\text{___}-\frac{7}{3}\)
- Responder
-
- \(>\)
- \(>\)
- \(<\)
- \(<\)
Ordene cada uno de los siguientes pares de números, usando\(<\) o\(>\).
- \(−1\text{___}-\frac{2}{3}\)
- \(−2\frac{1}{4}\text{___}-2\)
- \(−\frac{3}{5}\text{___}-\frac{4}{5}\)
- \(−4\text{___}-\frac{10}{3}\)
- Responder
-
- \(<\)
- \(<\)
- \(>\)
- \(<\)
Localizar decimales en la línea numérica
Dado que los decimales son formas de fracciones, ubicar decimales en la recta numérica es similar a ubicar fracciones en la recta numérica.
Localice 0.4 en la recta numérica.
- Responder
-
Una fracción propiamente dicha tiene un valor menor a uno. El número decimal\(0.4\) es equivalente a\(\frac{4}{10}\), una fracción propia, por lo que\(0.4\) se ubica entre 0 y 1. En una recta numérica, divida el intervalo entre 0 y 1 en 10 partes iguales. Ahora etiquetar las piezas\(0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0\). Escribimos 0 como 0.0 y 1 y 1.0, para que los números estén consistentemente en décimas. Por último, marcar\(0.4\) en la recta numérica. Ver Figura\(\PageIndex{6}\).

Figura\(\PageIndex{6}\)
Localizar en la recta numérica: 0.6.
- Contestar
-

Localizar en la recta numérica: 0.9.
- Contestar
-

Localizar\(−0.74\) en la línea numérica.
- Contestar
-
El decimal (−0.74\) es equivalente a\(-\frac{74}{100}\), por lo que se ubica entre 0 y −1. En una recta numérica, marque y etiquete las centésimas en el intervalo entre 0 y −1. Ver Figura\(\PageIndex{7}\).

Figura\(\PageIndex{7}\)
Localice en la recta numérica: −0.6.
- Contestar
-
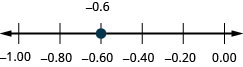
Localice en la recta numérica: −0.7.
- Contestar
-
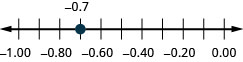
¿Cuál es más grande, 0.04 o 0.40? Si piensas en esto como dinero, sabes que $0.40 (cuarenta centavos) es mayor que $0.04 (cuatro centavos). Entonces,\(0.40 > 0.04\)
Nuevamente, podemos usar la línea numérica para ordenar números.
- \(a < b\)“a es menor que b” cuando a está a la izquierda de b en la recta numérica
- \(a > b\)“a es mayor que b” cuando a está a la derecha de b en la recta numérica
¿Dónde se encuentran 0.04 y 0.40 en la recta numérica? Ver Figura\(\PageIndex{8}\).

Vemos que 0.40 está a la derecha de 0.04 en la recta numérica. Esta es otra forma de demostrarlo\(0.40 > 0.04\).
¿Cómo se compara 0.31 con 0.308? Esto no se traduce en dinero para que sea fácil de comparar. Pero si convertimos 0.31 y 0.308 en fracciones, podemos decir cuál es más grande.
| 0.31 | 0.308 | |
| Convertir a fracciones. | \(\frac{31}{100}\) | \(\frac{308}{1000}\) |
| Necesitamos un denominador común para compararlos. | 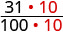 |
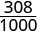 |
| \(\frac{310}{1000}\) | \(\frac{308}{1000}\) |
Porque\(310 > 308\), eso lo sabemos\(\frac{310}{1000} > \frac{308}{1000}\). Por lo tanto,\(0.31 > 0.308\).
Observe lo que hicimos\(0.31\) al convertir a una fracción, comenzamos con la fracción\(\frac{31}{100}\) y terminamos con la fracción\(\frac{310}{1000}\) equivalente.Convertir de\(\frac{310}{1000}\) nuevo a un decimal da 0.310. Entonces 0.31 equivale a 0.310. ¡Escribir ceros al final de un decimal no cambia su valor!
\[\frac { 31 } { 100 } = \frac { 310 } { 1000 } \quad \text { and } \quad 0.31 = 0.310\]
Decimos que 0.31 y 0.310 son decimales equivalentes.
Dos decimales son equivalentes si convierten a fracciones equivalentes.
Usamos decimales equivalentes cuando ordenamos decimales.
Aquí se resumen los pasos que tomamos para ordenar decimales.
- Escribe los números uno debajo del otro, alineando los puntos decimales.
- Comprueba si ambos números tienen el mismo número de dígitos. Si no, escribe ceros al final del que tenga menos dígitos para que coincidan.
- Compara los números como si fueran números enteros.
- Ordene los números usando el signo de desigualdad apropiado.
Ordene\(0.64 \text{ ___ } 0.6\) usando\(<\) o\(>\).
- Contestar
-
\(\begin{array} { ll } { \text {Write the numbers one under the other, } } &{0.64} \\ { \text {lining up the decimal points. } } &{0.6} \\ \\ { \text {Add a zero to 0.6 to make it a decimal } } &{0.64} \\ {\text{with 2 decimal places.}} &{0.60} \\ {\text{Now they are both hundredths.}} &{} \\ \\ {\text{64 is greater than 60.}} &{64 > 60} \\ \\ {\text{64 hundredths is greater than 60 hundredths.}} &{0.64 > 0.60} \\ \\ {} &{0.64 > 0.6}\end{array}\)
Ordene cada uno de los siguientes pares de números, usando\(<\) o\(>\):\(0.42 \text{ ___ } 0.4\).
- Contestar
-
\(>\)
Ordene cada uno de los siguientes pares de números, usando\(<\) o\(>\):\(0.18 \text{ ___ } 0.1\).
- Contestar
-
\(>\)
Ordene\(0.83 \text{ ___ } 0.803\) usando\(<\) o\(>\).
- Contestar
-
\(\begin{array} { ll } {} &{0.83\text{ ___ }0.803} \\ \\{ \text {Write the numbers one under the other, } } &{0.83} \\ { \text {lining up the decimal points. } } &{0.803} \\ \\ { \text {They do not have the same number of} } &{0.830} \\ {\text{digits.}} &{0.803} \\ {\text{Write one zero at the end of 0.83.}} &{} \\ \\ {\text{Since 830 > 803, 830 hundredths is}} &{0.830 > 0.803} \\ {\text{greater than 803 thousandths.}} &{}\\ \\ {} &{0.83 > 0.803}\end{array}\)
Ordene cada uno de los siguientes pares de números, usando\(<\) o\(>\):\(0.76 \text{ ___ } 0.706\).
- Contestar
-
\(>\)
Ordene cada uno de los siguientes pares de números, usando\(<\) o\(>\):\(0.305 \text{ ___ } 0.35\).
- Contestar
-
\(<\)
Cuando ordenamos decimales negativos, es importante recordar cómo ordenar enteros negativos. Recordemos que los números más grandes están a la derecha en la recta numérica. Por ejemplo, porque −2 se encuentra a la derecha de -3 en la recta numérica, lo sabemos\(−2>−3\). Del mismo modo, los números más pequeños se encuentran a la izquierda en la recta numérica. Por ejemplo, porque −9 se encuentra a la izquierda de −6 en la recta numérica, lo sabemos\(−9<−6\). Ver Figura\(\PageIndex{9}\).
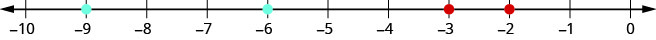
Si ampliamos el intervalo entre 0 y −1, como se muestra en Ejercicio\(\PageIndex{40}\), veríamos de la misma manera que\(−0.2>−0.3\) y\(−0.9<−0.6\).
Usar\(<\) o\(>\) ordenar\(−0.1\text{ ___ }−0.8\).
- Contestar
-
\(\begin{array} { ll } {} &{-0.1 \text{ ___ } -0.8} \\ \\ { \text { Write the numbers one under the other, lining up the } } &{-0.1} \\ { \text { decimal points. } } &{-0.8} \\ { \text { They have the same number of digits. } } &{} \\ \\ { \text { since } - 1 > - 8 , - 1 \text { tenth is greater than } - 8 \text { tenths. } } &{-0.1 > -0.8} \end{array}\)
Ordene el siguiente par de números, usando\(<\) o\(>\):\(−0.3\text{ ___ }−0.5\).
- Contestar
-
\(>\)
Ordene el siguiente par de números, usando\(<\) o\(>\):\(−0.6\text{ ___ }−0.7\).
- Contestar
-
\(>\)
Conceptos clave
- La notación de raíz cuadrada
\(\sqrt{m}\) se lee 'la raíz cuadrada de\(m\). ' Si\(m = n^{2}\), entonces\(\sqrt{m} = n\), para\(n \geq 0\). - Orden de decimales
- Escribe los números uno debajo del otro, alineando los puntos decimales.
- Comprueba si ambos números tienen el mismo número de dígitos. Si no, escribe ceros al final del que tenga menos dígitos para que coincidan.
- Compara los números como si fueran números enteros.
- Ordene los números usando el signo de desigualdad apropiado.
La práctica hace la perfección
Simplifique las expresiones con raíces cuadradas
En los siguientes ejercicios, simplifique.


