3.3: Resolver aplicaciones de mezcla

Última actualización
Guardar como PDF

Page ID: 110326

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Objetivos de aprendizaje

Al final de esta sección, podrás:

Resuelve problemas de palabras de monedas
Resolver problemas de palabras de boletos y sellos
Resolver problemas de mezcla
Utilice el modelo de mezcla para resolver problemas de inversión utilizando intereses simples

Nota

Antes de comenzar, toma este cuestionario de preparación.

Multiplicar:$14(0.25)$.
Si te perdiste este problema, revisa el Ejercicio 1.8.19.
Resolver:$0.25x+0.10(x+4)=2.5$.
Si te perdiste este problema, revisa el Ejercicio 2.4.22.
El número de monedas de diez centavos es tres más que el número de trimestres. Que q represente el número de trimestres. Escribe una expresión para el número de monedas de diez centavos.
Si te perdiste este problema, revisa Ejercicio 1.3.43.

Resolver problemas de monedas

En problemas de mezcla, tendremos dos o más ítems con diferentes valores para combinar juntos. El modelo de mezcla es utilizado por los tenderos y camareros para asegurarse de que establecen precios justos para los productos que venden. Muchos otros profesionales, como químicos, banqueros de inversión y paisajistas también utilizan el modelo de mezcla.

Nota

Hacer la actividad Matemáticas Manipulativas Coin Lab te ayudará a desarrollar una mejor comprensión de los problemas verbales de mezcla.

Empezaremos por mirar una aplicación con la que todos estén familiarizados: ¡dinero!

Imagina que sacamos un puñado de monedas de un bolsillo o monedero y las colocamos en un escritorio. ¿Cómo determinaríamos el valor de ese montón de monedas? Si podemos formar un plan paso a paso para encontrar el valor total de las monedas, nos ayudará a medida que comencemos a resolver problemas verbales de monedas.

Entonces, ¿qué haríamos? Para conseguir algo de orden al desorden de las monedas, podríamos separar las monedas en pilas de acuerdo a su valor. Los cuartos irían con cuartos, monedas de diez centavos con monedas de diez centavos, monedas de cinco centavos con monedas de cinco centavos, y así sucesivamente. Para obtener el valor total de todas las monedas, agregaríamos el valor total de cada pila.

Pilas de centavos, monedas de cinco centavos, monedas de diez centavos y cuartos — Figura$\PageIndex{1}$

¿Cómo determinaríamos el valor de cada pila? Piensa en la pila de diez centavos, ¿cuánto vale? Si contamos el número de monedas de diez centavos, sabremos cuántas tenemos, la cantidad de monedas de diez centavos.

Pero esto no nos dice el valor de todas las monedas de diez centavos. Digamos que contamos 17 dimes, ¿cuánto valen? Cada centavo vale $0.10—ese es el valor de una moneda de diez centavos. Para encontrar el valor total de la pila de 17 monedas de diez centavos, multiplica 17 por $0.10 para obtener $1.70. Este es el valor total de las 17 monedas de diez centavos. Este método lleva al siguiente modelo.

Valor total de monedas

Para el mismo tipo de moneda, el valor total de un número de monedas se encuentra utilizando el modelo

\[number\cdot value = total\space value\]

donde
número es el número de monedas

valor es el valor de cada moneda

el valor total es el valor total de todas las monedas

El número de monedas de diez centavos por el valor de cada moneda de diez centavos es igual al valor total de las monedas de diez centavos.

\[\begin{aligned} \text {number.} \cdot \text { value } &=\text { total value } \\ 17 \cdot \$ 0.10 &=\$ 1.70 \end{aligned}\]

Podríamos continuar con este proceso para cada tipo de moneda, y luego conoceríamos el valor total de cada tipo de moneda. Para obtener el valor total de todas las monedas, suma el valor total de cada tipo de moneda.

Veamos un caso específico. Supongamos que hay 14 cuartos, 17 dimes, 21 monedas de cinco centavos y 39 centavos.

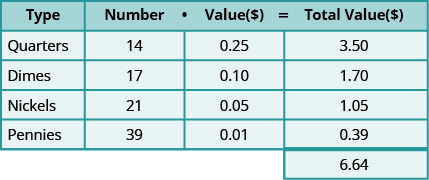
$Esta tabla tiene cinco filas y cuatro columnas con una celda extra en la parte inferior de la cuarta columna. La fila superior es una fila de encabezado que lee de izquierda a derecha Type, Number, Value ($) y Total Value ($). La segunda fila dice Cuartos, 14, 0.25 y 3.50. La tercera fila dice Dimes, 17, 0.10 y 1.70. La cuarta fila dice Nickels, 21, 0.05 y 1.05. La quinta fila dice Pennies, 39, 0.01 y 0.39. La celda extra lee 6.64.$

Mesa$\PageIndex{1}$

El valor total de todas las monedas es de $6.64.

¡Observe cómo el gráfico ayuda a organizar toda la información! Veamos cómo usamos este método para resolver un problema de palabras de moneda.

Ejemplo$\PageIndex{1}$

Adalberto tiene $2.25 en monedas de diez centavos y cinco centavos en el bolsillo. Tiene nueve cinco centavos más que diez centavos. ¿Cuántas de cada tipo de moneda tiene?

Solución

Paso 1. Lee el problema. Asegúrate de que todas las palabras e ideas sean entendidas.

Determinar los tipos de monedas involucradas.
Piensa en la estrategia que usamos para encontrar el valor del puñado de monedas. Lo primero que necesitamos es notar qué tipos de monedas están involucradas. Adalberto tiene monedas de diez centavos y cinco centavos. Crear una tabla para organizar la información. Consulte la tabla a continuación.

Etiquete las columnas “tipo”, “número”, “valor”, “valor total”.
Enumere los tipos de monedas.
Escribe en el valor de cada tipo de moneda.
Escribe en el valor total de todas las monedas.

Podemos trabajar este problema todo en centavos o en dólares. Aquí lo haremos en dólares y pondremos en el signo del dólar ($) en la tabla como recordatorio.
El valor de una moneda de diez centavos es de $0.10 y el valor de un níquel es de $0.05. El valor total de todas las monedas es de $2.25. La siguiente tabla muestra esta información.
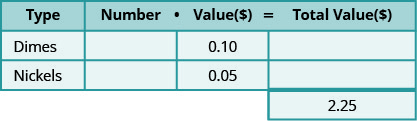
$Esta tabla tiene tres filas y cuatro columnas con una celda extra en la parte inferior de la cuarta columna. La fila superior es una fila de encabezado que lee de izquierda a derecha Type, Number, Value ($) y Total Value ($). La segunda fila dice Dimes, blank, 0.10 y blank. La tercera fila dice Nickels, blank, 0.05 y blank. La celda extra dice 2.25.$

Paso 2. Identificar lo que estamos buscando.

Se nos pide encontrar el número de monedas de diez y cinco centavos que tiene Adalberto.

Paso 3. Nombra lo que estamos buscando. Elija una variable para representar esa cantidad.

Usa expresiones variables para representar el número de cada tipo de moneda y escríbelas en la tabla.

Multiplique el número por el valor para obtener el valor total de cada tipo de moneda.

A continuación contamos el número de cada tipo de moneda. En este problema no podemos contar cada tipo de moneda —eso es lo que estás buscando— pero tenemos una pista. Hay nueve monedas más de cinco centavos que de diez centavos. El número de monedas de cinco centavos es nueve más que el número de monedas de diez centavos.

\[\begin{aligned} \text { Let } d &=\text { number of dimes. } \\ d+9 &=\text { number of nickels } \end{aligned}\]

Rellene la columna “número” en la tabla para ayudar a organizar todo.

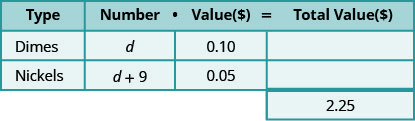
$Esta tabla tiene tres filas y cuatro columnas con una celda extra en la parte inferior de la cuarta columna. La fila superior es una fila de encabezado que lee de izquierda a derecha Type, Number, Value ($) y Total Value ($). La segunda fila dice Dimes, d, 0.10 y en blanco. La tercera fila dice Níqueles, d más 9, 0.05 y en blanco. La celda extra dice 2.25.$

¡Ahora tenemos toda la información que necesitamos del problema!

Multiplicamos el número por el valor para obtener el valor total de cada tipo de moneda. Si bien no conocemos el número real, sí tenemos una expresión para representarlo.

Y así ahora multiplicar$\text{number}\cdot\text{value}=\text{total value}$. Vea cómo se hace esto en la tabla a continuación.

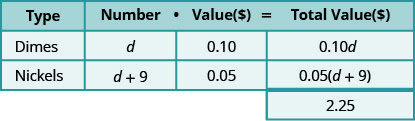
$Esta tabla tiene tres filas y cuatro columnas con una celda extra en la parte inferior de la cuarta columna. La fila superior es una fila de encabezado que lee de izquierda a derecha Type, Number, Value ($) y Total Value ($). La segunda fila dice Dimes, d, 0.10 y 0.10d. La tercera fila dice Níqueles, d más 9, 0.05 y 0.05 veces la cantidad (d más 9). La celda extra dice 2.25.$

Observe que hicimos que el encabezamiento de la mesa muestre el modelo.

Paso 4. Traducir en una ecuación. Puede ser útil reafirmar el problema en una oración. Traducir la oración en inglés en una ecuación algebraica.

Escribe la ecuación sumando los valores totales de todos los tipos de monedas.

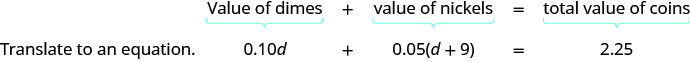
$La frase, “valor de diez centavos más valor de cinco centavos es igual al valor total de las monedas”, puede traducirse en una ecuación. Traduzca “value of dimes” a 0.10d, traduzca “value of nickles” a 0.05d, y traduzca “valor total de monedas” a 2.25. La ecuación completa es 0.10d más 0.05 veces la cantidad d más 9 es igual a 2.25.$

Paso 5. Resolver la ecuación usando buenas técnicas de álgebra.

Ahora resuelve esta ecuación.	$.$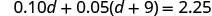
Distribuir.	$.$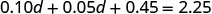
Combina términos similares.	$.$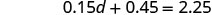
Restar 0.45 de cada lado.	$.$
Dividir.	$.$
Por lo que hay 12 dimes.
El número de monedas de cinco centavos es d+9d+9.	$.$
	$.$
	21

Paso 6. Comprueba la respuesta en el problema y asegúrate de que tenga sentido.

¿Esto comprueba?

\[\begin{array}{llll}{12 \text { dimes }} & {12(0.10)} &{=} &{1.20} \\ {21 \text { nickels }} & {21(0.05)} & {=} &{\underline{1.05}} \\ {} &{} &{}&{$ 2.25\checkmark} \end{array}\]

Paso 7. Contesta la pregunta con una oración completa.

Adalberto tiene doce monedas de diez centavos y veintiún monedas de cinco centavos.

Si esto fuera un ejercicio de tarea, nuestro trabajo podría verse como el siguiente.

$Una tarea escrita en papel de hoja suelta forrada. El encargo dice: “Adalberto tiene 2 dólares y 25 centavos en monedas de diez centavos y cinco centavos en el bolsillo. Tiene nueve cinco centavos más que diez centavos. ¿Cuántos de cada tipo tiene?” Debajo de esto hay una tabla. La primera fila de la tabla es una fila de encabezado, y cada celda nombra la columna o columnas debajo de ella. La primera celda de la izquierda se llama “Tipo”. La segunda celda contiene la ecuación “Número” por “Valor” es igual a “Valor total”, con una columna correspondiente a “Número”, una columna correspondiente a “Valor” y una columna correspondiente al valor total. De ahí que el contenido de la columna “Número” multiplicado por el contenido de la columna “Valor” sea igual al contenido de la columna “Valor total”. En la segunda fila de la tabla, la columna “Tipo” contiene “Dimes”, la columna “Número” contiene d, la columna “Valor” contiene 0.10 y la columna “Valor total” contiene 0.10d. En la tercera fila de la tabla, la columna “Tipo” contiene “Níqueles”, la columna “Número” contiene d más 9, la columna “Valor contiene 0.05, y la columna “Valor total” contiene 0.05 veces la cantidad d más 9. Una fila hacia abajo, la columna “Valor total” contiene una celda más, que contiene 2.25. Debajo de la tabla se encuentra la ecuación 0.10d más 0.05d más 0.45 es igual a 2.25. Por debajo de esto se encuentra 0.15d más 0.45 es igual a 2.25. Por debajo de esto se encuentra 0.15d es igual a 1.80. A la derecha está d más 9, lo que se traduce en 12 más 9, o 21 nickels. A la derecha de esto está la etapa de comprobación, donde vemos si 12 centavos y 21 nickels ascienden a 2 dólares y 25 centavos. 12 veces 0.10 es igual a 1.20, y 21 veces (0.05) es igual a 1.05. 1.20 más 1.05 es igual a 2.25.$

Pruébalo$\PageIndex{1}$

Michaela tiene $2.05 en monedas de diez centavos y cinco centavos en su monedero. Tiene siete monedas de diez centavos más que de cinco centavos. ¿Cuántas monedas de cada tipo tiene?

Contestar: 9 níqueles, 16 dimes

Pruébalo$\PageIndex{2}$

Liliana tiene $2.10 en monedas de cinco centavos y cuartos en su mochila. Tiene 12 monedas más de cinco centavos que cuartos. ¿Cuántas monedas de cada tipo tiene?

Contestar: 17 níqueles, 5 cuartos

Resolver problemas de palabras de monedas.

Lee el problema. Asegúrate de que todas las palabras e ideas sean entendidas.
- Determinar los tipos de monedas involucradas.
- Crear una tabla para organizar la información.
- Etiquete las columnas “tipo”, “número”, “valor”, “valor total”.
- Enumere los tipos de monedas.
- Escribe en el valor de cada tipo de moneda.
- Escribe en el valor total de todas las monedas.
Identificar lo que estamos buscando.
Nombra lo que estamos buscando. Elija una variable para representar esa cantidad.
- Usa expresiones variables para representar el número de cada tipo de moneda y escríbelas en la tabla.
- Multiplique el número por el valor para obtener el valor total de cada tipo de moneda.
Traducir en una ecuación.
Puede ser útil reafirmar el problema en una oración con toda la información importante. Después, traduzca la oración en una ecuación.
Escribe la ecuación sumando los valores totales de todos los tipos de monedas.
Resolver la ecuación usando buenas técnicas de álgebra.
Comprueba la respuesta en el problema y asegúrate de que tenga sentido.
Contesta la pregunta con una oración completa.

Ejemplo$\PageIndex{2}$

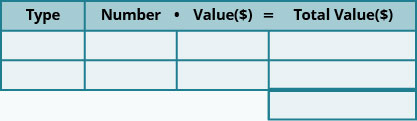
María tiene $2.43 en cuartos y centavos en su billetera. Ella tiene el doble de centavos que cuartos. ¿Cuántas monedas de cada tipo tiene?

Solución

Paso 1. Lee el problema.

Determinar los tipos de monedas involucradas.

Sabemos que María tiene cuartos y centavos.

Crear una tabla para organizar la información.

Paso 2. Identifica lo que buscas.
- Estamos buscando el número de cuartos y centavos.
Paso 3. Nombre. Representar el número de cuartos y centavos usando variables.
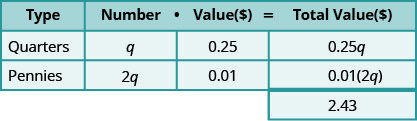
- Multiplica el 'número' y el 'valor' para obtener el 'valor total' de cada tipo de moneda. $Sin texto Alt$
  Paso 4. Traducir. Escribe la ecuación sumando el 'valor total' de todos los tipos de monedas.
  
  $\begin{array} {ll} {\textbf{Step5. Solve} \text{ the equation.}} &{0.25q + 0.01(2q) = 2.43} \\{\text{Multiply.}} &{0.25q + 0.02q = 2.43} \\ {\text{Combine like terms.}} &{0.27q = 2.43} \\ {\text{Divide by 0.27}} &{q = 9 \text{ quarters}} \\ {\text{The number of pennies is 2q.}} &{2q} \\ {} &{2\cdot 9} \\ {} &{18 \text{ pennies}} \\ {\textbf{Step 6. Check} \text{ the answer in the problem.}} &{} \\\\ {\text{Maria has 9 quarters and 18 pennies. Dies this}} &{} \\ {\text{make }$2.43?} &{} \end{array}$
  $\begin{array} {llll}\\ {9\text{ quarters }} &{ 9(0.25)} &{=} &{2.25} \\ {18\text{ pennies }} &{18(0.01)} &{=} &{\underline{0.18}} &{}\\ {\text{Total}} &{} &{} &{$2.43\checkmark} \end{array}$
  $\begin{array} {ll} \\ {\textbf{Step 7. Answer}\text{ the question.}} &{\text{Maria has nine quarters and eighteen pennies.}} \end{array}$

Pruébalo$\PageIndex{3}$

Sumanta tiene $4.20 en monedas de cinco centavos y diez centavos en su alcancía. Ella tiene el doble de cinco centavos que diez centavos. ¿Cuántas monedas de cada tipo tiene?

Contestar: 42 níqueles, 21 dimes

Pruébalo$\PageIndex{4}$

Alison tiene tres veces más monedas de diez centavos que cuartos en su bolso. Ella tiene $9.35 en total. ¿Cuántas monedas de cada tipo tiene?

Contestar: 51 dimes, 17 trimestres

En el siguiente ejemplo, mostraremos solo la tabla terminada; recuerde los pasos que tomamos para rellenar la tabla.

Ejemplo$\PageIndex{3}$

Danny tiene centavos y monedas de cinco centavos por valor de $2.14 en su alcancía. El número de monedas de cinco centavos es dos más de diez veces el número de centavos. ¿Cuántas monedas de cinco centavos y cuántos centavos tiene Danny?

Solución

Paso 1. Lee el problema.
Determinar los tipos de monedas involucradas.	centavos y cinco centavos
Crear una tabla.
Escribe en el valor de cada tipo de moneda.	Los centavos valen $0.01. Las monedas de níquel valen 0.05 dólares.
Paso 2. Identificar lo que estamos buscando.	el número de centavos y monedas de cinco centavos
Paso 3. Nombre. Representar el número de cada tipo de moneda utilizando variables.
El número de monedas de cinco centavos se define en términos del número de centavos, así que empieza con centavos.	Dejar$p=$ número de centavos.
El número de monedas de cinco centavos es dos más de diez veces el número de centavos.	Y vamos$10p+2=$ número de monedas de cinco centavos.
Multiplica el número y el valor para obtener el valor total de cada tipo de moneda.
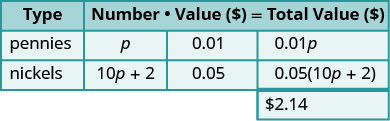$Esta tabla tiene tres filas y cuatro columnas con una celda extra en la parte inferior de la cuarta columna. La fila superior es una fila de encabezado que lee de izquierda a derecha Type, Number, Value ($) y Total Value ($). La segunda fila dice centavos, p, 0.01 y 0.01p. La tercera fila dice níqueles, 10p más 2, 0.05 y 0.05 veces la cantidad (10p más 2). El celular extra dice $2.14.$
Paso 4. Traducir. Escribe la ecuación sumando el valor total de todos los tipos de monedas.	$.$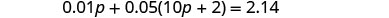
Paso 5. Resuelve la ecuación.	$.$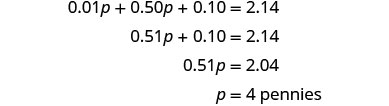
¿Cuántas cinco centavos?	$.$
Paso 6. Comprueba la respuesta en el problema y asegúrate de que tenga sentido Danny tiene cuatro centavos y 42 monedas de cinco centavos. ¿El valor total es $2.14? $\begin{array}{rll} {4(0.01)+42(0.05)} &{\stackrel{?}{=}} &{2.14} \\ {2.14} &{=} &{2.14\checkmark} \end{array}$
Paso 7. Contesta la pregunta.	Danny tiene cuatro centavos y 42 monedas de cinco centavos.

Pruébalo$\PageIndex{5}$

Jesse tiene 6.55 dólares en cuartos y monedas de cinco centavos en el bolsillo. El número de monedas de cinco centavos es más de cinco veces el número de trimestres. ¿Cuántas monedas y cuántos cuartos tiene Jesse?

Contestar: 41 níqueles, 18 cuartos

Pruébalo$\PageIndex{6}$

Elane tiene un total de $7.00 en monedas de diez centavos y cinco centavos en su frasco de monedas. El número de monedas de diez centavos que tiene Elane es siete menos de tres veces el número de monedas de cinco centavos. ¿Cuántas de cada moneda tiene Elane?

Contestar: 22 níqueles, 59 dimes

Resolver problemas de palabras de boletos y sellos

Los problemas que involucran boletos o sellos son muy parecidos a los problemas de monedas. Cada tipo de boleto y sello tiene un valor, tal como lo hace cada tipo de moneda. Entonces, para resolver estos problemas, seguiremos los mismos pasos que usamos para resolver problemas de monedas.

Ejemplo$\PageIndex{4}$

En un concierto escolar, el valor total de los boletos vendidos fue de 1.506 dólares. Los boletos de estudiante se venden por $6 cada uno y los boletos para adultos por $9 cada uno. El número de boletos de adulto vendidos fue cinco menos de tres veces el número de boletos de estudiante vendidos. ¿Cuántos boletos de estudiante y cuántos boletos de adulto se vendieron?

Solución

Paso 1. Lee el problema.

Determinar los tipos de boletos involucrados. Hay boletos para estudiantes y boletos para adultos.
Crear una tabla para organizar la información.

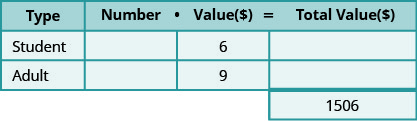
$Esta tabla tiene tres filas y cuatro columnas con una celda extra en la parte inferior de la cuarta columna. La fila superior es una fila de encabezado que lee de izquierda a derecha Type, Number, Value ($) y Total Value ($). La segunda fila dice Estudiante, en blanco, 6 y en blanco. La tercera fila dice Adulto, en blanco, 9 y en blanco. La celda extra dice 1506.$

Paso 2. Identificar lo que estamos buscando.

Estamos buscando el número de boletos para estudiantes y adultos.

Paso 3. Nombre. Representar el número de cada tipo de ticket utilizando variables.

Sabemos que el número de boletos para adultos vendidos fue cinco menos de tres veces el número de boletos de estudiante vendidos.

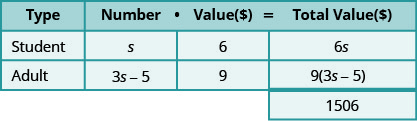
Multiplique el número por el valor para obtener el valor total de cada tipo de boleto. $Esta tabla tiene tres filas y cuatro columnas con una celda extra en la parte inferior de la cuarta columna. La fila superior es una fila de encabezado que lee de izquierda a derecha Type, Number, Value ($) y Total Value ($). La segunda fila dice Estudiante, s, 6 y 6s. La tercera fila dice Adulto, 3s menos 5, 9 y 9 veces la cantidad (3s menos 5). La celda extra dice 1506.$
Paso 4. Traducir. Escribe la ecuación sumando los valores totales de cada tipo de ticket.

\[6 s+9(3 s-5)=1506 \nonumber\]

Paso 5. Resuelve la ecuación.

\[\begin{array}{rcl}{6 s+27 s-45} &{=} &{1506} \\ {33 s-45} &{=} &{1506} \\ {33 s} &{=} &{1551} \\ {s} & {=} &{47 \text { student tickets }} \\ {\text{Number of adult tickets}} &{=} &{3s-5} \\ {} &{=} &{3(47)-5} \\ {\text{So there were}} &{136} &{\text{adult tickets}}\end{array} \nonumber\]

Paso 6. Consulta la respuesta.

Había 47 boletos de estudiante a $6 cada uno y 136 boletos para adultos a $9 cada uno. ¿El valor total es 1,506$? Encontramos el valor total de cada tipo de boleto multiplicando el número de boletos por su valor luego sumamos para obtener el valor total de todos los boletos vendidos.

\[\begin{array}{lll} {47\cdot 6} &{=} &{282} \\ {136\cdot 9} &{=} &{\underline{1224}} \\ {} &{} &{1506\checkmark} \\\end{array} \nonumber\]

Paso 7. Contesta la pregunta. Vendieron 47 boletos de estudiante y 136 boletos de adultos.

Pruébalo$\PageIndex{7}$

El primer día de un torneo de waterpolo el valor total de los boletos vendidos fue de $17,610. Los pases de un día se venden por $20 y los pases de torneo se venden por $30. El número de pases de torneo vendidos fue 37 más que el número de pases de día vendidos. ¿Cuántos pases de día y cuántos pases de torneo se vendieron?

Contestar: 330 pases diarios, 367 pases para torneos

Pruébalo$\PageIndex{8}$

En el cine, el valor total de los boletos vendidos fue de $2,612.50. Los boletos para adultos se venden por $10 cada uno y los boletos para adultos/niños se venden por $7.50 cada uno El número de boletos mayores/niños vendidos fue de 25 menos del doble del número de boletos de adultos vendidos. ¿Cuántos boletos para adultos mayores y niños y cuántos boletos de adultos se vendieron?

Contestar: 112 boletos adultos, 199 boletos senior/niño

Hemos aprendido a encontrar el número total de boletos cuando el número de un tipo de boleto se basa en el número del otro tipo. A continuación, veremos un ejemplo donde conocemos el número total de boletos y tenemos que averiguar cómo se relacionan los dos tipos de boletos.

Supongamos que Bianca vendió un total de 100 boletos. Cada boleto era un boleto de adulto o un boleto infantil. Si vendió 20 boletos infantiles, ¿cuántos boletos para adultos vendió?

¿Dijías '80'? ¿Cómo lo averiguaste? ¿Le restaste 20 de 100?

Si vendía 45 boletos infantiles, ¿cuántos boletos para adultos vendió?

¿Dijías '55'? ¿Cómo lo encontraste? ¿Al restar 45 de 100?

¿Y si vendió 75 boletos infantiles? ¿Cuántos boletos para adultos vendió?

El número de boletos para adultos debe ser de 100−75. Vendió 25 boletos para adultos.

Ahora, supongamos que Bianca vendió x boletos infantiles. Entonces, ¿cuántos boletos para adultos vendió? Para averiguarlo, seguiríamos la misma lógica que usamos anteriormente. En cada caso, restamos el número de boletos infantiles de 100 para obtener el número de boletos de adultos. Ahora hacemos lo mismo con x.

Esto lo hemos resumido a continuación.

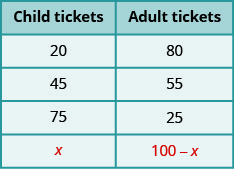
$Esta tabla tiene cinco filas y dos columnas. La fila superior es una fila de cabecera que lee de izquierda a derecha boletos para niños y boletos para adultos. La segunda fila dice 20 y 80. La tercera fila dice 45 y 55. La cuarta fila dice 75 y 25. La quinta fila dice x y 100 más x.$

Mesa$\PageIndex{2}$

Podemos aplicar estas técnicas a otros ejemplos

Ejemplo$\PageIndex{5}$

Galeno vendió 810 boletos para el carnaval de su iglesia por un total de $2,820. Los boletos para niños cuestan $3 cada uno y los boletos para adultos cuestan $5 cada uno. ¿Cuántos boletos infantiles y cuántos boletos de adultos vendió?

Solución

Paso 1. Lee el problema.

Determinar los tipos de boletos involucrados. Hay boletos para niños y boletos para adultos.
Crear una tabla para organizar la información.

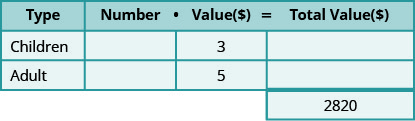
$Esta tabla tiene tres filas y cuatro columnas con una celda extra en la parte inferior de la cuarta columna. La fila superior es una fila de encabezado que lee de izquierda a derecha Tipo, Número, Valor ($) y Valor total ($). La segunda fila dice Niños, en blanco, 3 y en blanco. La tercera fila dice Adulto, en blanco, 5 y en blanco. La celda extra lee 2820.$

Paso 2. Identificar lo que estamos buscando.

Estamos buscando el número de boletos para niños y adultos.

Paso 3. Nombre. Representar el número de cada tipo de ticket utilizando variables.

Sabemos que el total de boletos vendidos fue 810.
Esto significa que el número de boletos infantiles más el número de boletos para adultos deben sumar 810.
Deja$c$ ser el número de boletos infantiles.

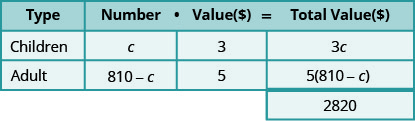
$Esta tabla tiene tres filas y cuatro columnas con una celda extra en la parte inferior de la cuarta columna. La fila superior es una fila de encabezado que lee de izquierda a derecha Tipo, Número, Valor ($) y Valor total ($). La segunda fila dice Niños, c, 3 y 3c. La tercera fila dice Adulto, 810 menos c, 5 y 5 veces la cantidad (810 menos c). La celda extra lee 2820.$

Entonces$810−c$ es el número de boletos para adultos.
Multiplique el número por el valor para obtener el valor total de cada tipo de boleto.

Paso 4. Traducir.

Escribe la ecuación sumando los valores totales de cada tipo de ticket.

Paso 5. Resuelve la ecuación.

\[\begin{align*} 3 c+5(810-c) &=2,820 \\ 3 c+4,050-5 c &=2,820 \\-2 c &=-1,230 \\ c &=615 \text { children tickets } \end{align*}\]

¿Cuántos adultos?

\[\begin{array}{c}{810-c} \\ {810-615} \\ {195 \text { adult tickets }}\end{array} \nonumber\]

Paso 6. Consulta la respuesta. Había 615 boletos infantiles a $3 cada uno y 195 boletos para adultos a $5 cada uno. ¿El valor total es 2.820$?

\[\begin{array}{rrl}{615 \cdot 3} &{=} & {1845} \\ {195 \cdot 5} &{=} & {\underline{975}} \\ {} &{} &{2,820\checkmark} \end{array} \nonumber\]

Paso 7. Contesta la pregunta. Galen vendió 615 boletos infantiles y 195 boletos para adultos.

Pruébalo$\PageIndex{9}$

Durante su turno en la taquilla del museo, Leah vendió 115 boletos por un total de $1,163. Los boletos para adultos cuestan $12 y los boletos para estudiantes cuestan $5. ¿Cuántos boletos para adultos y cuántos boletos de estudiante vendió Leah?

Contestar: 84 boletos para adultos, 31 boletos para estudiantes

Pruébalo$\PageIndex{10}$

Un barco de observación de ballenas tenía 40 pasajeros que pagaban a bordo. El total recaudado de los boletos fue de $1,196. Los pasajeros con tarifa completa pagaron $32 cada uno y los pasajeros con tarifa reducida pagaron $26 cada uno. ¿Cuántos pasajeros de tarifa completa y cuántos pasajeros de tarifa reducida había en el barco?

Contestar: 26 tarifa completa, 14 tarifa reducida

Ahora, haremos uno donde llenemos la mesa todos a la vez.

Ejemplo$\PageIndex{6}$

Mónica pagó 8.36 dólares por timbres. El número de sellos de 41 centavos fue de cuatro más del doble del número de sellos de dos centavos. ¿Cuántos sellos de 41 centavos y cuántos sellos de dos centavos compró Mónica?

Solución

Los tipos de sellos son sellos de 41 centavos y sellos de dos centavos. ¡Sus nombres también dan el valor!

“El número de sellos de 41 centavos fue de cuatro más del doble del número de sellos de dos centavos”.

\[\begin{array}{l}{\text { Let } x=\text { number of } 2 \text { -cent stamps. }} \\ {2 x+4=\text { number of } 41-\text { cent stamps }}\end{array} \nonumber\]

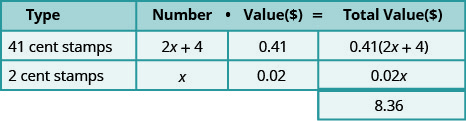
$Esta tabla tiene tres filas y cuatro columnas con una celda extra en la parte inferior de la cuarta columna. La fila superior es una fila de encabezado que lee de izquierda a derecha Tipo, Número, Valor ($) y Valor total ($). En la segunda fila se lee sellos de 41 centavos, 2x más 4, 0.41 y 0.41 veces la cantidad (2x más 4). La tercera fila dice sellos de 2 centavos, x, 0.02 y 0.02x. La celda extra dice 8.36.$

\[\begin{array}{lr} {\text{Write the equation from the total values.}} &{0.41(2x + 4) + 0.02x = 8.36} \\ {} &{0.82x + 1.64 + 0.02x = 8.36} \\ {} &{0.84x + 1.64 = 8.36} \\ {\text{Solve the equation.}} &{0.84x = 6.72} \\ {} &{x = 8} \\\\ {\text{Monica bought eight two-cent stamps.}} &{} \\{\text{Find the number of 41-cent stamps she bought}} &{2x + 4 \text{ for } x = 8} \\{\text{by evaluating}} &{2x + 4} \\{} &{2(8) + 4} \\ {} &{20} \end{array} \nonumber\]

Cheque.

\[\begin{array} {rll} {8(0.02) + 20(0.41)} &{\stackrel{?}{=}} &{8.36} \\ {0.16 + 8.20} &{\stackrel{?}{=}} &{8.36} \\{8.36} &{=} &{8.46\checkmark} \end{array}\]
\[\begin{array} {ll} \\ {} &{\text{Monica bought eight two-cent stamps and 20}} \\ {} &{\text{41-cent stamps}} \end{array} \nonumber\]

Pruébalo$\PageIndex{11}$

Eric pagó 13.36 dólares por timbres. El número de sellos de 41 centavos fue ocho más del doble del número de sellos de dos centavos. ¿Cuántos sellos de 41 centavos y cuántos sellos de dos centavos compró Eric?

Contestar: 32 a $0.41, 12 a $0.02

Pruébalo$\PageIndex{12}$

Kailee pagó 12.66 dólares por timbres. El número de sellos de 41 centavos fue cuatro menos de tres veces el número de sellos de 20 centavos. ¿Cuántos sellos de 41 centavos y cuántos sellos de 20 centavos compró Kailee?

Contestar: 26 a $0.41, 10 a $0.20

Resolver problemas de mezcla

Ahora resolveremos algunas aplicaciones más generales del modelo de mezcla. Los tenderos y camareros utilizan el modelo de mezcla para establecer un precio justo para un producto hecho a partir de la mezcla de dos o más ingredientes. Los planificadores financieros utilizan el modelo de mezcla cuando invierten dinero en una variedad de cuentas y quieren encontrar la tasa de interés general. Los paisajistas utilizan el modelo de mezcla cuando tienen un surtido de plantas y un presupuesto fijo, y los coordinadores de eventos hacen lo mismo al elegir aperitivos y entradas para un banquete.

Nuestro primer problema de palabras de mezcla será hacer una mezcla de trail a partir de pasas y nueces.

Ejemplo$\PageIndex{7}$

Henning está mezclando pasas y nueces para hacer 10 libras de mezcla de trail. Las pasas cuestan $2 la libra y las nueces cuestan $6 la libra. Si Henning quiere que su costo para el trail mix sea de $5.20 la libra, ¿cuántas libras de pasas y cuántas libras de nueces debe usar?

Solución

Como antes, rellenamos un cuadro para organizar nuestra información.

Las 10 libras de mezcla de trail provendrán de mezclar pasas y nueces.

\[\begin{array}{l}{\text { Let } x=\text { number of pounds of raisins. }} \\ {10-x=\text { number of pounds of nuts }}\end{array} \nonumber\]

Ingresamos el precio por libra para cada artículo.

Multiplicamos el número por el valor para obtener el valor total.

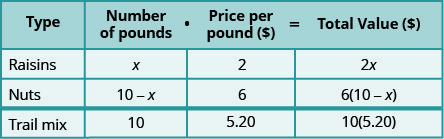
$Esta tabla tiene cuatro filas y cuatro columnas. La fila superior es una fila de encabezado que dice de izquierda a derecha Tipo, Número de libras, Precio por libra ($) y Valor Total ($). La segunda fila dice pasas, x, 2 y 2x. La tercera fila dice nueces, 10 menos x, 6 y 6 veces la cantidad (10 menos x). En la cuarta fila se lee trail mix, 10, 5.20 y 10 veces 5.20.$

Observe que la última línea de la tabla da la información de la cantidad total de la mezcla.

Sabemos que el valor de las pasas más el valor de los frutos secos será el valor de la mezcla de trail.

Escribe la ecuación a partir de los valores totales.	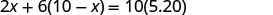$Ejemplo3.32.jpg$
Resuelve la ecuación.	$.$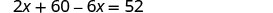
	$.$
	$.$
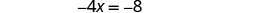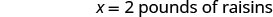Encuentra el número de libras de nueces.	$.$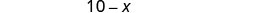
	$.$
	8 libras de nueces
Cheque. $\begin{array}{rll} {2($2) + 8($6)} &{\stackrel{?}{=} } &{10($5.20)} \\ {$4 + $48} &{\stackrel{?}{=} } &{$52} \\ {$52} &{=} &{$52\checkmark} \end{array}$
	Henning mezcló dos libras de pasas con ocho libras de nueces.

Pruébalo$\PageIndex{13}$

Orlando está mezclando nueces y cuadrados de cereales para hacer una mezcla de fiesta. Las nueces se venden por $7 la libra y los cuadrados de cereales se venden por $4 la libra. Orlando quiere hacer 30 libras de mezcla de fiesta a un costo de $6.50 la libra, ¿cuántas libras de nueces y cuántas libras de cuadrados de cereales debe usar?

Contestar: 5 libras cuadrados de cereales, 25 libras de nueces

Pruébalo$\PageIndex{14}$

Becca quiere mezclar jugo de frutas y refrescos para hacer un ponche. Ella puede comprar jugo de frutas por $3 el galón y refresco por $4 el galón. Si quiere hacer 28 galones de ponche a un costo de $3.25 el galón, ¿cuántos galones de jugo de frutas y cuántos galones de refresco debe comprar?

Contestar: 21 galones de ponche de fruta, 7 galones de refresco

También podemos utilizar el modelo de mezcla para resolver problemas de inversión utilizando interés simple. Hemos utilizado la fórmula de interés simple,$I=Prt$, donde$t$ representaba el número de años. Cuando sólo necesitamos encontrar el interés por un año,$t=1$, entonces entonces$I=Pr$.

Ejemplo$\PageIndex{8}$

Stacey tiene 20,000 dólares para invertir en dos cuentas bancarias diferentes. Una cuenta paga intereses al 3% anual y la otra cuenta paga intereses al 5% anual. ¿Cuánto debería invertir en cada cuenta si quiere ganar 4.5% de interés anual sobre el monto total?

Solución

Llenaremos un cuadro para organizar nuestra información. Utilizaremos la fórmula de interés simple para encontrar los intereses devengados en las diferentes cuentas.

El interés sobre la inversión mixta vendrá de sumar los intereses de la cuenta ganando 3% y los intereses de la cuenta ganando 5% para obtener el interés total sobre los 20,000 dólares.

\[\begin{aligned} \text { Let } x &=\text { amount invested at } 3 \% \\ 20,000-x &=\text { amount invested at } 5 \% \end{aligned}\]

El monto invertido es el principal de cada cuenta.

Ingresamos la tasa de interés para cada cuenta.

Multiplicamos la cantidad invertida por la tasa para obtener el interés.

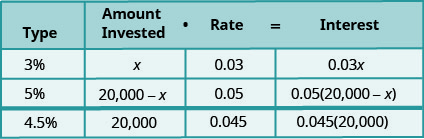
$Esta tabla tiene cuatro filas y cuatro columnas. La fila superior es una fila de encabezado que dice de izquierda a derecha Tipo, Monto invertido, Tasa e Interés. La segunda fila dice 3%, x, 0.03 y 0.03x. La tercera fila dice 5%, 20,000 menos x, 0.05 y 0.05 veces la cantidad (20,000 menos x). La cuarta fila dice 4.5%, 20,000, 0.045 y 0.045 veces 20,000.$

Observe que el monto total invertido, 20,000, es la suma del monto invertido al 3% y el monto invertido al 5%. Y el interés total,$0.045(20,000)$, es la suma de los intereses ganados en la cuenta del 3% y los intereses devengados en la cuenta del 5%.

Al igual que con las otras aplicaciones de mezcla, la última columna de la tabla nos da la ecuación a resolver.

Escribe la ecuación a partir de los intereses devengados. Resuelve la ecuación.	$\begin{array}{rll}{0.03x + 0.05(20000-x)} &{=} &{0.045(20000)} \\\\ {0.03x + 1000 - 0.05x} &{=} &{900} \\ {-0.02x} &{=} &{-100} \\ {x} &{=} &{5000} \\ {\text{amount invested at 3%}} \end{array}$
Encuentra la cantidad invertida en 5%.	$.$ $.$ $.$
Cheque. $\begin{array}{rll} {0.03x + 0.05(15000 + x)} &{\stackrel{?}{=} } &{0.045(20000)} \\ {150 + 750} &{\stackrel{?}{=} } &{900} \\ {900} &{=} &{900\checkmark} \end{array}$
	Stacey debería invertir $5,000 en la cuenta que gana 3% y $15,000 en la cuenta que gana 5%.

Pruébalo$\PageIndex{15}$

Remy tiene $14,000 para invertir en dos fondos mutuos. Un fondo paga intereses al 4% anual y el otro fondo paga intereses al 7% anual. ¿Cuánto debería invertir en cada fondo si quiere ganar 6.1% de interés sobre el monto total?

Contestar: $4,200 al 4%, $9,800 al 7%

Pruébalo$\PageIndex{16}$

Marco tiene $8,000 para ahorrar para la educación universitaria de su hija. Quiere dividirlo entre una cuenta que paga 3.2% de interés anual y otra cuenta que paga 8% de interés anual. ¿Cuánto debería invertir en cada cuenta si quiere que el interés sobre la inversión total sea de 6.5%?

Contestar: $2,500 al 3.2%, $5,500 al 8%

Conceptos clave

Valor Total de Monedas Para el mismo tipo de moneda, el valor total de un número de monedas se encuentra utilizando el modelo.
número·valor=valor total donde número es el número de monedas y valor es el valor de cada moneda; valor total es el valor total de todas las monedas
Estrategia de resolución de problemas—Problemas de palabras de monedas
1. Lee el problema. Hacer que se entiendan todas las palabras e ideas. Determinar los tipos de monedas involucradas.
  - Crear una tabla para organizar la información.
  - Etiquete las columnas tipo, número, valor, valor total.
  - Enumere los tipos de monedas.
  - Escribe en el valor de cada tipo de moneda.
  - Escribe en el valor total de todas las monedas.
2. Identificar lo que estamos buscando.
3. Nombra lo que estamos buscando. Elija una variable para representar esa cantidad.
  Usa expresiones variables para representar el número de cada tipo de moneda y escríbelas en la tabla.
  Multiplique el número por el valor para obtener el valor total de cada tipo de moneda.
4. Traducir en una ecuación. Puede ser útil reafirmar el problema en una oración con toda la información importante. Después, traduzca la oración en una ecuación.
  Escribe la ecuación sumando los valores totales de todos los tipos de monedas.
5. Resolver la ecuación usando buenas técnicas de álgebra.
6. Comprueba la respuesta en el problema y asegúrate de que tenga sentido.
7. Contesta la pregunta con una oración completa.

Glosario

problemas de mezcla: Los problemas de mezcla combinan dos o más artículos con diferentes valores juntos.

Search

Text Color

Text Size

Margin Size

Font Type

Nota

Valor total de monedas

Ejemplo\(\PageIndex{1}\)

Pruébalo\(\PageIndex{1}\)

Pruébalo\(\PageIndex{2}\)

Resolver problemas de palabras de monedas.

Ejemplo\(\PageIndex{2}\)

Pruébalo\(\PageIndex{3}\)

Pruébalo\(\PageIndex{4}\)

Ejemplo\(\PageIndex{3}\)

Pruébalo\(\PageIndex{5}\)

Pruébalo\(\PageIndex{6}\)

Ejemplo\(\PageIndex{4}\)

Pruébalo\(\PageIndex{7}\)

Pruébalo\(\PageIndex{8}\)

Ejemplo\(\PageIndex{5}\)

Pruébalo\(\PageIndex{9}\)

Pruébalo\(\PageIndex{10}\)

Ejemplo\(\PageIndex{6}\)

Pruébalo\(\PageIndex{11}\)

Pruébalo\(\PageIndex{12}\)

Ejemplo\(\PageIndex{7}\)

Pruébalo\(\PageIndex{13}\)

Pruébalo\(\PageIndex{14}\)

Ejemplo\(\PageIndex{8}\)

Pruébalo\(\PageIndex{15}\)

Pruébalo\(\PageIndex{16}\)

Escribe la ecuación a partir de los intereses devengados. Resuelve la ecuación.	\(\begin{array}{rll}{0.03x + 0.05(20000-x)} &{=} &{0.045(20000)} \\\\ {0.03x + 1000 - 0.05x} &{=} &{900} \\ {-0.02x} &{=} &{-100} \\ {x} &{=} &{5000} \\ {\text{amount invested at 3%}} \end{array}\)
Encuentra la cantidad invertida en 5%.	$.$ $.$ $.$
Cheque. \(\begin{array}{rll} {0.03x + 0.05(15000 + x)} &{\stackrel{?}{=} } &{0.045(20000)} \\ {150 + 750} &{\stackrel{?}{=} } &{900} \\ {900} &{=} &{900\checkmark} \end{array}\)
	Stacey debería invertir $5,000 en la cuenta que gana 3% y $15,000 en la cuenta que gana 5%.