Capítulo 3 Ejercicios de revisión
- Page ID
- 110292
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Capítulo 3 Ejercicios de revisión
3.1 Uso de una estrategia de resolución de problemas
Abordar problemas de palabras con una actitud positiva
En los siguientes ejercicios, reflexiona sobre tu acercamiento a los problemas de palabras.
¿Cómo ha cambiado su actitud hacia la solución de problemas de palabras como resultado de trabajar en este capítulo? Explique.
- Contestar
-
las respuestas variarán
¿La estrategia de resolución de problemas te ayudó a resolver problemas de palabras en este capítulo? Explique.
Usar una estrategia de resolución de problemas para problemas de palabras
En los siguientes ejercicios, resuelve usando la estrategia de resolución de problemas para problemas de palabras. Recuerda escribir una oración completa para responder a cada pregunta.
Tres cuartas partes de las personas en un concierto son niños. Si hay 87 niños, ¿cuál es el número total de personas en el concierto?
- Contestar
-
116
Hay nueve saxofonistas en la banda. El número de saxofonistas es uno menos del doble del número de jugadores de tuba. Encuentra el número de jugadores de tuba.
Resolver problemas de números
En los siguientes ejercicios, resuelve cada problema de palabra numérica.
La suma de un número y tres es cuarenta y uno. Encuentra el número.
- Contestar
-
38
Dos veces la diferencia de un número y diez es cincuenta y cuatro. Encuentra el número.
Un número es nueve menos que otro. Su suma es negativa veintisiete. Encuentra los números.
- Contestar
-
−18, −9
Un número es once más que otro. Si su suma se incrementa en diecisiete, el resultado es 90. Encuentra los números.
Un número es dos más de cuatro veces otro. Su suma es −13. Encuentra los números.
- Contestar
-
−3, −10
La suma de dos números enteros consecutivos es −135. Encuentra los números.
Encuentra tres enteros consecutivos cuya suma es −141.
- Contestar
-
−48, −47, −46
Encuentra tres enteros pares consecutivos cuya suma sea 234.
Encuentra tres enteros impares consecutivos cuya suma es 51.
- Contestar
-
15, 17, 19
Koji tiene $5,502 en su cuenta de ahorros. Esto es $30 menos que seis veces el monto en su cuenta corriente. ¿Cuánto dinero tiene Koji en su cuenta corriente?
3.2 Resolver porcentaje de aplicaciones
Traducir y resolver ecuaciones básicas de porcentaje
En los siguientes ejercicios, traduzca y resuelva.
¿Qué número es 67% de 250?
- Contestar
-
167.5
¿300% de 82 es qué número?
¿12.5% de qué número es 20?
- Contestar
-
160
¿72 es 30% de qué número?
¿Cuál por ciento de 125 es 150?
- Contestar
-
120%
127.5 es ¿qué porcentaje de 850?
Resolver porcentaje de aplicaciones
En los siguientes ejercicios, resuelve.
La factura del almuerzo de Dino era de $19.45. Quería dejar como propina el 20% del total de la factura. ¿Cuánto debería ser la propina?
- Contestar
-
3,89
Reza estaba muy enfermo y perdió 15% de su peso original. Perdió 27 libras. ¿Cuál era su peso original?
Dolores compró una cuna a la venta por 350 dólares. El precio de venta fue del 40% del precio original. ¿Cuál era el precio original de la cuna?
- Contestar
-
$875
Jaden gana 2 680 por mes. Paga $938 mensuales por renta. ¿Qué porcentaje de su paga mensual va a la renta?
Encuentre aumento porcentual y disminución porcentual
En los siguientes ejercicios, resuelve.
Angel tiene un aumento en su sueldo anual de 55.400 dólares a 56.785 dólares. Encuentra el incremento porcentual.
- Contestar
-
2.5%
La factura mensual de gasolina de Rowena bajó de $83.75 el mes pasado a $56.95 este mes. Encuentra la disminución porcentual.
Resolver aplicaciones de interés simple
En los siguientes ejercicios, resuelve.
Winston depositó $3,294 en una cuenta bancaria con tasa de interés 2.6%. ¿Cuánto interés se ganó en 5 años?
- Contestar
-
$428.22
Moira le pidió prestados 4.500 dólares a su abuelo para pagar su primer año de universidad. Tres años después, ella reembolsó los $4,500 más 243 intereses. ¿Cuál era la tasa de interés?
El estado de cuenta del préstamo para refrigerador de Jaime dijo que pagaría $1,026 en intereses por un préstamo a 4 años en 13.5%. ¿Cuánto pidió prestado Jaime para comprar el refrigerador?
- Contestar
-
$1,900
En 12 años, un bono que pagó 6.35% de intereses ganó $7,620 intereses. ¿Cuál fue el principal del vínculo?
Resolver aplicaciones con descuento o margen
En los siguientes ejercicios, encuentra el precio de venta.
El precio original de un bolso era de 84 dólares. Carole lo compró a la venta por $21 de descuento.
- Contestar
-
$63
Marian quiere comprar una mesa de café que cuesta 495 dólares. La próxima semana la mesa de centro estará a la venta por $149 de descuento.
En los siguientes ejercicios, encuentra
- la cantidad de descuento y
- el precio de venta.
Emmett compró un par de zapatos a la venta al 40% de descuento sobre un precio original de 138 dólares.
- Contestar
-
- $55.20
- $82.80
Anastasia compró un vestido a la venta al 75% de descuento con un precio original de 280 dólares.
En los siguientes ejercicios, encuentra ⓐ la cantidad de descuento y ⓑ la tasa de descuento. (Redondear a la décima de porcentaje más cercana, si es necesario.)
Zack compró una impresora para su oficina que estaba a la venta por 380 dólares. El precio original de la impresora era de 450 dólares.
- Contestar
-
- $70
- 15.6%
Lacey compró un par de botas a la venta por 95 dólares. El precio original de las botas era de $200.
En los siguientes ejercicios, encuentra
- el importe del margen de beneficio y
- el precio de lista.
Nga y Lauren compraron un cofre en un mercadillo por 50 dólares. Lo volvieron a terminar y luego agregaron un margen de 350%.
- Contestar
-
- $175
- $225
Carly compró agua embotellada por $0.24 por botella en la tienda de descuento. Añadió un margen de 75% antes de venderlos en el partido de futbol.
3.3 Resolver aplicaciones de mezcla
Solucionar problemas verbales de monedas
En los siguientes ejercicios, resuelve cada problema de palabras de moneda.
Francie tiene $4.35 en monedas de diez centavos y trimestres. El número de diez centavos es cinco más que el número de trimestres. ¿Cuántas de cada moneda tiene?
- Contestar
-
16 dimes, 11 trimestres
Scott tiene $0.39 en centavos y monedas de cinco centavos. El número de centavos es ocho veces el número de monedas de cinco centavos. ¿Cuántas de cada moneda tiene?
Paulette tiene $140 en billetes de $5 y $10. El número de billetes de $10 es uno menos del doble del número de billetes de $5. ¿Cuántos de cada uno tiene?
- Contestar
-
seis billetes de $5, 11 billetes de $10
Lenny tiene $3.69 en centavos, monedas de diez centavos y cuartos. El número de centavos es tres más que el número de diez centavos. El número de trimestres es el doble del número de monedas de diez centavos. ¿Cuántas de cada moneda tiene?
Resolver problemas de palabras de boletos y sellos
En los siguientes ejercicios, resuelve cada boleto o sello problema de palabras.
Un almuerzo en la iglesia hizo $842. Los boletos para adultos cuestan $10 cada uno y los boletos para niños cuestan $6 cada uno. El número de niños fue de 12 más del doble del número de adultos. ¿Cuántos de cada boleto se vendieron?
- Contestar
-
35 adultos, 82 niños
Los boletos para un juego de basquetbol cuestan $2 para estudiantes y $5 para adultos. El número de estudiantes fue tres menos de 10 veces el número de adultos. El monto total de dinero de la venta de boletos fue de 619 dólares. ¿Cuántos de cada boleto se vendieron?
Se vendieron 125 boletos para el concierto de la banda de jazz por un total de 1.022 dólares. Los boletos de estudiante cuestan $6 cada uno y los boletos de admisión general cuestan $10 cada uno. ¿Cuántos de cada tipo de boleto se vendieron?
- Contestar
-
57 alumnos, 68 adultos
Una tarde el parque acuático vendió 525 boletos por un total de $13,545. Los boletos para niños cuestan $19 cada uno y los boletos para adultos cuestan $40 cada uno. ¿Cuántos de cada tipo de boleto se vendieron?
Ana gastó $4.06 comprando sellos. El número de sellos de $0.41 que compró fue cinco más que el número de sellos de $0.26. ¿Cuántos de cada uno compró?
- Contestar
-
tres sellos de $0.26, ocho $0.41 sellos
Yumi gastó $34.15 comprando sellos. El número de sellos de $0.56 que compró fue 10 menos de cuatro veces el número de sellos de $0.41. ¿Cuántos de cada uno compró?
Solucionar problemas verbales de mezcla
En los siguientes ejercicios, resuelve cada problema de mezcla de palabras.
Marquese está haciendo 10 libras de mezcla de trail a partir de pasas y nueces. Las pasas cuestan $3.45 por libra y las nueces cuestan $7.95 por libra. ¿Cuántas libras de pasas y cuántas libras de nueces debe usar Marquese para la mezcla de trail para costarle $6.96 por libra?
- Contestar
-
2.2 lb. de pasas, 7.8 lb. de frutos secos
Amber quiere poner azulejos en el salpicadero de los mostradores de su cocina. Ella necesitará 36 pies cuadrados de azulejo. Ella usará azulejos básicos que cuestan $8 por pie cuadrado y azulejos decoradores que cuestan $20 por pie cuadrado. ¿Cuántos pies cuadrados de cada baldosa debe usar para que el costo total del backsplash sea de $10 por pie cuadrado?
Shawn tiene $15,000 para invertir. Ella pondrá parte de ello en un fondo que paga 4.5% de intereses anuales y el resto en un certificado de depósito que paga 1.8% de interés anual. ¿Cuánto debería invertir en cada cuenta si quiere ganar 4.05% de interés anual sobre el monto total?
- Contestar
-
$12,500 al 4.5%, $2,500 al 1.8%
Enrique pidió prestados 23,500 dólares para comprar un auto. Le paga a su tío el 2% de interés sobre los 4.500 dólares que le pidió prestados, y le paga al banco 11.5% de intereses sobre el resto. ¿Qué tasa de interés promedio paga sobre el total de $23,500? (Redondea tu respuesta al décimo por ciento más cercano.)
3.4 Aplicaciones de Resolver Geometría: Triángulos, Rectángulos y Teorema de Pitágoras
Resolver aplicaciones usando propiedades de triángulo
En los siguientes ejercicios, resuelve usando propiedades de triángulo.
Las medidas de dos ángulos de un triángulo son 22 y 85 grados. Encuentra la medida del tercer ángulo.
- Contestar
-
73°
El área de juegos en un centro comercial es un triángulo con un perímetro de 48 pies. Las longitudes de dos lados son 19 pies y 14 pies. ¿Cuánto dura el tercer lado?
Una señal vial triangular tiene una base de 30 pulgadas y una altura de 40 pulgadas. ¿Cuál es su área?
- Contestar
-
600 pulgadas cuadradas
¿Cuál es la altura de un triángulo con área 67.5 metros cuadrados y base 9 metros?
Un ángulo de un triángulo es 30° más que el ángulo más pequeño. El ángulo más grande es la suma de los otros ángulos. Encuentra las medidas de los tres ángulos.
- Contestar
-
30°,60°,90°
Un ángulo de un triángulo rectángulo mide 58°. ¿Cuál es la medida de los otros ángulos del triángulo?
La medida del ángulo más pequeño en un triángulo rectángulo es 45° menos que la medida del siguiente ángulo más grande. Encuentra las medidas de los tres ángulos.
- Contestar
-
22.5°,67.5°,90°
El perímetro de un triángulo es de 97 pies. Un lado del triángulo es once pies más que el lado más pequeño. El tercer lado es seis pies más del doble del lado más pequeño. Encuentra las longitudes de todos los lados.
Usa el Teorema de Pitágoras
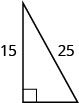
En los siguientes ejercicios, utilice el Teorema de Pitágoras para encontrar la longitud de la hipotenusa.
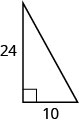
- Contestar
-
26
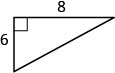
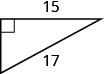
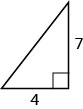
En los siguientes ejercicios, usa el Teorema de Pitágoras para encontrar la longitud del lado faltante. Redondear a la décima más cercana, si es necesario.
- Contestar
-
8
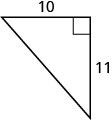
- Contestar
-
8.1
En los siguientes ejercicios, resuelve. Aproximado a la décima más cercana, si es necesario.
Sergio necesita fijar un cable para sujetar la antena al techo de su casa, como se muestra en la figura. La antena mide 8 pies de altura y Sergio tiene 10 pies de cable. ¿A qué distancia de la base de la antena puede fijar el cable?
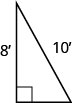
- Contestar
-
\(6^{\prime}\)
Seong está construyendo estanterías en su cochera. Las repisas son de 36 pulgadas de ancho y 15 pulgadas de alto. Quiere poner un corsé diagonal en la espalda para estabilizar las repisas, como se muestra. ¿Cuánto tiempo debe durar el corsé?
Resolver aplicaciones usando propiedades de rectángulo
En los siguientes ejercicios, resuelve usando propiedades de rectángulo.
La longitud de un rectángulo es de 36 pies y el ancho es de 19 pies. Encuentra el
- perímetro
- área.
- Contestar
-
- 110 pies
- 684 pies cuadrados
Una acera frente a la casa de Kathy tiene la forma de un rectángulo de cuatro pies de ancho por 45 pies de largo. Encuentra el
- perímetro
- área.
El área de un rectángulo es de 2356 metros cuadrados. La longitud es de 38 metros. ¿Cuál es el ancho?
- Contestar
-
62 m
El ancho de un rectángulo es de 45 centímetros. El área es de 2,700 centímetros cuadrados. ¿Cuál es la longitud?
El largo de un rectángulo es 12 cm más que el ancho. El perímetro es de 74 cm. Encuentra el largo y el ancho.
- Contestar
-
24.5 cm, 12.5 cm
El ancho de un rectángulo es tres más del doble de la longitud. El perímetro es de 96 pulgadas. Encuentra el largo y el ancho.
3.5 Resolver aplicaciones de movimiento uniforme
Resolver aplicaciones de movimiento uniforme
En los siguientes ejercicios, resuelve.
Cuando Gabe conduce de Sacramento a Redding le toma 2.2 horas. Elsa tarda 2 horas en conducir a la misma distancia. La velocidad de Elsa es siete millas por hora más rápida que la velocidad de Gabe. Encuentra la velocidad de Gabe y la velocidad de Elsa.
- Contestar
-
Gabe 70 mph, Elsa 77 mph
Louellen y Tracy se conocieron en un restaurante en la carretera entre Chicago y Nashville. Louellen había salido de Chicago y condujo 3.2 horas hacia Nashville. Tracy había salido de Nashville y condujo 4 horas hacia Chicago, a una velocidad una milla por hora más rápida que la velocidad de Louellen. La distancia entre Chicago y Nashville es de 472 millas. Encuentra la velocidad de Louellen y la velocidad de Tracy.
Dos autobuses salen de Amarillo al mismo tiempo. El autobús de Albuquerque se dirige hacia el oeste por la I-40 a una velocidad de 72 millas por hora, y el autobús de Oklahoma City se dirige hacia el este por la I-40 a una velocidad de 78 millas por hora. ¿Cuántas horas les llevará estar a 375 millas de distancia?
- Contestar
-
2.5 horas
Kyle remó su bote río arriba durante 50 minutos. Le tomó 30 minutos volver a remar río abajo. Su velocidad que va aguas arriba es dos millas por hora más lenta que su velocidad que va aguas abajo. Encuentra las velocidades aguas arriba y aguas abajo de Kyle.
A las 6:30, Devon salió de su casa y montó su bicicleta en la carretera llana hasta las 7:30. Entonces ella comenzó a montar cuesta arriba y cabalgó hasta las 8:00. Ella recorrió un total de 15 millas. Su velocidad en la carretera plana era tres millas por hora más rápida que su velocidad subiendo cuesta arriba. Encuentra la velocidad de Devon en la carretera plana y sube cuesta arriba.
- Contestar
-
carretera plana 11 mph, cuesta arriba 8 mph
Anthony condujo de la ciudad de Nueva York a Baltimore, a una distancia de 192 millas. Salió a las 3:45 y tuvo mucho tránsito hasta las 5:30. El tráfico fue ligero para el resto del viaje, y llegó a las 7:30. Su velocidad en el tráfico ligero era de cuatro millas por hora más del doble de su velocidad en el tráfico pesado. Encuentra la velocidad de manejo de Anthony en tráfico pesado y tráfico ligero.
3.6 Resolver aplicaciones con desigualdades lineales
Resolver aplicaciones con desigualdades lineales
En los siguientes ejercicios, resuelve.
Julianne tiene un presupuesto semanal de comida de 231 dólares para su familia. Si planea presupuestar la misma cantidad para cada uno de los siete días de la semana, ¿cuál es la cantidad máxima que puede gastar en comida cada día?
- Contestar
-
$33 por día
Rogelio pinta acuarelas. Obtuvo una tarjeta de regalo de 100 dólares a la tienda de suministros de arte y quiere usarla para comprar\(12^{\prime \prime} \times 16^{\prime \prime}\) lienzos. Cada lienzo cuesta $10.99. ¿Cuál es el número máximo de lienzos que puede comprar con su tarjeta regalo?
A Briana se le ha ofrecido un trabajo de ventas en otra ciudad. La oferta fue por $42,500 más 8% de sus ventas totales. Para que merezca la pena la mudanza, Briana necesita tener un salario anual de al menos 66,500 dólares. ¿Cuáles necesitarían ser sus ventas totales para que se mudara?
- Contestar
-
al menos $300,000
El auto de Renee le cuesta 195 dólares mensuales más $0.09 por milla. ¿Cuántas millas puede conducir Renee para que sus gastos mensuales de automóvil no superen los 250 dólares?
Costa es contador. Durante la temporada de impuestos, cobra 125 dólares para hacer una simple declaración de impuestos. Sus gastos por la compra de software, el alquiler de una oficina y la publicidad son de $6,000. ¿Cuántas declaraciones de impuestos debe hacer si quiere obtener una ganancia de al menos $8,000?
- Contestar
-
al menos 112 empleos
Jenna está planeando unas vacaciones en un resort de 5 días con tres de sus amigas. Le costará 279 dólares por pasajes aéreos, $300 por comida y entretenimiento, y 65 dólares diarios por su parte del hotel. Tiene 550 dólares ahorrados para sus vacaciones y puede ganar 25 dólares por hora como asistente en el estudio de fotografía de su tío. ¿Cuántas horas debe trabajar para tener suficiente dinero para sus vacaciones?
Prueba de práctica
Cuatro quintas partes de las personas en una caminata son niños. Si hay 12 niños, ¿cuál es el número total de personas en la caminata?
- Contestar
-
15
Un número es tres más que dos veces otro. Su suma es −63. Encuentra los números.
La suma de dos enteros impares consecutivos es −96. Encuentra los números.
- Contestar
-
−49, −47
El desayuno de Marla era de 525 calorías. Esto fue 35% de sus calorías totales para el día. ¿Cuántas calorías tenía ese día?
El pago por hora de Humberto aumentó de 16.25 dólares a 17.55 dólares. Encuentra el incremento porcentual.
- Contestar
-
8%
Melinda depositó $5,985 en una cuenta bancaria con una tasa de interés del 1.9%. ¿Cuánto interés se ganó en 2 años?
Dotty compró un congelador a la venta por 486.50 dólares. El precio original del congelador era de 695 dólares. Encuentra
- la cantidad de descuento y
- la tasa de descuento.
- Contestar
-
- $208.50
- 30%
Bonita tiene $2.95 en monedas de diez centavos y cuartos en el bolsillo. Si tiene cinco monedas de diez centavos más que cuartos, ¿cuántas de cada moneda tiene?
En un concierto se vendieron mil 600 dólares en boletos. Los boletos para adultos fueron de $9 cada uno y los boletos para niños fueron de $4 cada uno. Si el número de boletos para adultos era 30 menos del doble del número de boletos infantiles, ¿cuántos de cada tipo se vendieron?
- Contestar
-
140 adultos, 85 niños
Kim está haciendo ocho galones de ponche con jugo de frutas y refrescos. El jugo de fruta cuesta $6.04 por galón y el refresco cuesta $4.28 por galón. ¿Cuánto jugo de frutas y cuánto refresco debe usar para que el ponche cueste $5.71 por galón?
La medida de un ángulo de un triángulo es el doble de la medida del ángulo más pequeño. La medida del tercer ángulo es 14 más que la medida del ángulo más pequeño. Encuentra las medidas de los tres ángulos.
- Contestar
-
41.5°,55.5°,83°
¿Cuál es la altura de un triángulo con área 277.2 pulgadas cuadradas y base 44 pulgadas?
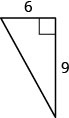
En los siguientes ejercicios, usa el Teorema de Pitágoras para encontrar la longitud del lado faltante. Redondear a la décima más cercana, si es necesario.
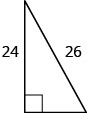
- Contestar
-
10
Un diamante de béisbol es realmente un cuadrado con lados de 90 pies. ¿Qué tan lejos está del plato casero a la segunda base, como se muestra?
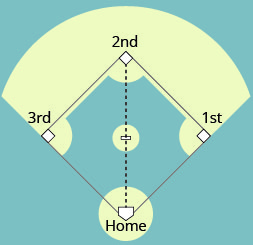
- Contestar
-
127.3 pies
La longitud de un rectángulo es de dos pies más de cinco veces el ancho. El perímetro es de 40 pies. Encuentra las dimensiones del rectángulo.
Dos aviones salen de Dallas al mismo tiempo. Uno se dirige hacia el este a una velocidad de 428 millas por hora. El otro avión se dirige hacia el oeste a una velocidad de 382 millas por hora. ¿Cuántas horas les llevará estar a 2,025 millas de distancia?
- Contestar
-
2.5 horas
León condujo desde su casa en Cincinnati hasta la casa de su hermana en Cleveland, a una distancia de 252 millas. Le tomó 412412 horas. Durante la primera media hora tuvo mucho tráfico, y el resto del tiempo su velocidad era de cinco millas por hora menos del doble de su velocidad en el tráfico pesado. ¿Cuál era su velocidad en el tráfico pesado?
Chloe tiene un presupuesto de 800 dólares para disfraces para los 18 integrantes de su grupo de teatro musical. ¿Cuál es el máximo que puede gastar por cada disfraz?
- Contestar
-
a lo sumo $44.44 por disfraz
Frank encontró una oferta de autos de alquiler en línea por $49 por semana más $0.24 por milla. ¿Cuántas millas podría conducir si quiere que el costo total de una semana no sea superior a $150?