4.11: Ortogonalidad
- Page ID
- 114506
- Determinar si un conjunto dado es ortogonal u ortonormal.
- Determinar si una matriz dada es ortogonal.
- Dado un conjunto linealmente independiente, utilice el Proceso Gram-Schmidt para encontrar los conjuntos ortogonales y ortonormales correspondientes.
- Encuentra la proyección ortogonal de un vector sobre un subespacio.
- Encuentra la aproximación de mínimos cuadrados para una colección de puntos.
En esta sección, examinamos lo que significa que los vectores (y conjuntos de vectores) sean ortogonales y ortonormales. En primer lugar, es necesario revisar algunos conceptos importantes. Puede recordar las definiciones para el lapso de un conjunto de vectores y un conjunto lineal independiente de vectores. Incluimos las definiciones y ejemplos aquí para mayor comodidad.
La colección de todas las combinaciones lineales de un conjunto de vectores\(\{ \vec{u}_1, \cdots ,\vec{u}_k\}\) en\(\mathbb{R}^{n}\) se conoce como el lapso de estos vectores y se escribe como\(\mathrm{span} \{\vec{u}_1, \cdots , \vec{u}_k\}\).
Llamamos a una colección de la forma\(\mathrm{span} \{\vec{u}_1, \cdots , \vec{u}_k\}\) un subespacio de\(\mathbb{R}^{n}\).
Considera el siguiente ejemplo.
Describir el lapso de los vectores\(\vec{u}=\left[ \begin{array}{rrr} 1 & 1 & 0 \end{array} \right]^T\) y\(\vec{v}=\left[ \begin{array}{rrr} 3 & 2 & 0 \end{array} \right]^T \in \mathbb{R}^{3}\).
Solución
Se puede ver que cualquier combinación lineal de los vectores\(\vec{u}\) y\(\vec{v}\) produce un vector\(\left[ \begin{array}{rrr} x & y & 0 \end{array} \right]^T\) en el\(XY\) plano -.
Además, cada vector en el\(XY\) plano es de hecho una combinación lineal de los vectores\(\vec{u}\) y\(\vec{v}\). Eso es porque\[\left[ \begin{array}{r} x \\ y \\ 0 \end{array} \right] = (-2x+3y) \left[ \begin{array}{r} 1 \\ 1 \\ 0 \end{array} \right] + (x-y)\left[ \begin{array}{r} 3 \\ 2 \\ 0 \end{array} \right]\nonumber \]
Así span\(\{\vec{u},\vec{v}\}\) es precisamente el\(XY\) -plano.
El lapso de un conjunto de vectores en\(\mathbb{R}^n\) es lo que llamamos un subespacio de\(\mathbb{R}^n\). Un subespacio\(W\) se caracteriza por la característica de que cualquier combinación lineal de vectores\(W\) es nuevamente un vector contenido en\(W\).
Otra propiedad importante de los conjuntos de vectores se llama independencia lineal.
Se dice que un conjunto de vectores distintos de cero\(\{ \vec{u}_1, \cdots ,\vec{u}_k\}\) en\(\mathbb{R}^{n}\) es linealmente independiente si ningún vector en ese conjunto está en el lapso de los otros vectores de ese conjunto.
Aquí hay un ejemplo.
Considerar vectores\(\vec{u}=\left[ \begin{array}{rrr} 1 & 1 & 0 \end{array} \right]^T\),\(\vec{v}=\left[ \begin{array}{rrr} 3 & 2 & 0 \end{array} \right]^T\), y\(\vec{w}=\left[ \begin{array}{rrr} 4 & 5 & 0 \end{array} \right]^T \in \mathbb{R}^{3}\). Verificar si el conjunto\(\{\vec{u}, \vec{v}, \vec{w}\}\) es linealmente independiente.
Solución
Ya verificamos en Ejemplo\(\PageIndex{1}\) que\(\mathrm{span} \{\vec{u}, \vec{v} \}\) es el\(XY\) -plano. Dado que claramente también\(\vec{w}\) está en el\(XY\) plano -, entonces el conjunto no\(\{\vec{u}, \vec{v}, \vec{w}\}\) es linealmente independiente.
En términos de expansión, un conjunto de vectores es linealmente independiente si no contiene vectores innecesarios. En el ejemplo anterior se puede ver que el vector\(\vec{w}\) no ayuda a abarcar ningún vector nuevo que no esté ya en el lapso de los otros dos vectores. Sin embargo puedes verificar que el conjunto\(\{\vec{u}, \vec{v}\}\) es linealmente independiente, ya que no obtendrás el\(XY\) -plane como el span de un solo vector.
También podemos determinar si un conjunto de vectores es linealmente independiente examinando combinaciones lineales. Un conjunto de vectores es linealmente independiente si y solo si siempre que una combinación lineal de estos vectores sea igual a cero, se deduce que todos los coeficientes son iguales a cero. Es un buen ejercicio para verificar esta equivalencia, y esta última condición se suele utilizar como definición (equivalente) de independencia lineal.
Si un subespacio es abarcado por un conjunto linealmente independiente de vectores, entonces decimos que es una base para el subespacio.
Que\(V\) sea un subespacio de\(\mathbb{R}^{n}\). Entonces\(\left\{ \vec{u}_{1},\cdots ,\vec{u}_{k}\right\}\) es una base para\(V\) si se mantienen las siguientes dos condiciones.
- \(\mathrm{span}\left\{ \vec{u}_{1},\cdots ,\vec{u}_{k}\right\} =V\)
- \(\left\{ \vec{u}_{1},\cdots ,\vec{u}_{k}\right\}\)es linealmente independiente
Así, el conjunto\(\{\vec{u}, \vec{v}\}\) de vectores de Ejemplo\(\PageIndex{2}\) es una base para\(XY\) -plane in\(\mathbb{R}^{3}\) ya que es linealmente independiente y abarca el\(XY\) -plano.
Recordemos de las propiedades del punto producto de vectores que dos vectores\(\vec{u}\) y\(\vec{v}\) son ortogonales si\(\vec{u} \cdot \vec{v} = 0\). Supongamos que un vector es ortogonal a un conjunto de expansión de\(\mathbb{R}^n\). ¿Qué se puede decir de tal vector? Esta es la discusión en el siguiente ejemplo.
Vamos\(\{\vec{x}_1, \vec{x}_2, \ldots, \vec{x}_k\}\in\mathbb{R}^n\) y supongamos\(\mathbb{R}^n=\mathrm{span}\{\vec{x}_1, \vec{x}_2, \ldots, \vec{x}_k\}\). Además, supongamos que existe un vector\(\vec{u}\in\mathbb{R}^n\) para el cual\(\vec{u}\cdot \vec{x}_j=0\) para todos\(j\),\(1\leq j\leq k\). ¿Qué tipo de vector es\(\vec{u}\)?
Solución
Escribe\(\vec{u}=t_1\vec{x}_1 + t_2\vec{x}_2 +\cdots +t_k\vec{x}_k\) para algunos\(t_1, t_2, \ldots, t_k\in\mathbb{R}\) (esto es posible porque\(\vec{x}_1, \vec{x}_2, \ldots, \vec{x}_k\) span\(\mathbb{R}^n\)).
Entonces
\[\begin{aligned} \| \vec{u} \| ^2 & = \vec{u}\cdot\vec{u} \\ & = \vec{u}\cdot(t_1\vec{x}_1 + t_2\vec{x}_2 +\cdots +t_k\vec{x}_k) \\ & = \vec{u}\cdot (t_1\vec{x}_1) + \vec{u}\cdot (t_2\vec{x}_2) + \cdots + \vec{u}\cdot (t_k\vec{x}_k) \\ & = t_1(\vec{u}\cdot \vec{x}_1) + t_2(\vec{u}\cdot \vec{x}_2) + \cdots + t_k(\vec{u}\cdot \vec{x}_k) \\ & = t_1(0) + t_2(0) + \cdots + t_k(0) = 0.\end{aligned}\]
Ya que\( \| \vec{u} \| ^2 =0\),\( \| \vec{u} \| =0\). Sabemos que\( \| \vec{u} \| =0\) si y sólo si\(\vec{u}=\vec{0}_n\). Por lo tanto,\(\vec{u}=\vec{0}_n\). En conclusión, el único vector ortogonal a cada vector de un conjunto de expansión de\(\mathbb{R}^n\) es el vector cero.
Ahora podemos discutir qué se entiende por un conjunto ortogonal de vectores.
Dejar\(\{ \vec{u}_1, \vec{u}_2, \cdots, \vec{u}_m \}\) ser un conjunto de vectores en\(\mathbb{R}^n\). Entonces este conjunto se llama un conjunto ortogonal si se mantienen las siguientes condiciones:
- \(\vec{u}_i \cdot \vec{u}_j = 0\)para todos\(i \neq j\)
- \(\vec{u}_i \neq \vec{0}\)para todos\(i\)
Si tenemos un conjunto ortogonal de vectores y normalizamos cada vector para que tengan longitud 1, el conjunto resultante se denomina conjunto ortonormal de vectores. Se pueden describir de la siguiente manera.
Un conjunto de vectores,\(\left\{ \vec{w}_{1},\cdots ,\vec{w}_{m}\right\}\) se dice que es un conjunto ortonormal si\[\vec{w}_i \cdot \vec{w}_j = \delta _{ij} = \left\{ \begin{array}{c} 1\text{ if }i=j \\ 0\text{ if }i\neq j \end{array} \right.\nonumber \]
Tenga en cuenta que todos los conjuntos ortonormales son ortogonales, pero lo contrario no es necesariamente cierto ya que los vectores pueden no estar normalizados. Para normalizar los vectores, simplemente necesitamos dividir cada uno por su longitud.
La normalización de un conjunto ortogonal es el proceso de convertir un conjunto ortogonal (pero no ortonormal) en un conjunto ortonormal. Si\(\{ \vec{u}_1, \vec{u}_2, \ldots, \vec{u}_k\}\) es un subconjunto ortogonal de\(\mathbb{R}^n\), entonces\[\left\{ \frac{1}{ \| \vec{u}_1 \| }\vec{u}_1, \frac{1}{ \| \vec{u}_2 \| }\vec{u}_2, \ldots, \frac{1}{ \| \vec{u}_k \| }\vec{u}_k \right\}\nonumber \] es un conjunto ortonormal.
Ilustramos este concepto en el siguiente ejemplo.
Considera el conjunto de vectores dado por\[\left\{ \vec{u}_1, \vec{u}_2 \right\} = \left\{ \left[ \begin{array}{c} 1 \\ 1 \end{array} \right], \left[ \begin{array}{r} -1 \\ 1 \end{array} \right] \right\}\nonumber \] Mostrar que es un conjunto ortogonal de vectores pero no uno ortonormal. Encuentra el conjunto ortonormal correspondiente.
Solución
Uno fácilmente verifica eso\(\vec{u}_1 \cdot \vec{u}_2 = 0\) y\(\left\{ \vec{u}_1, \vec{u}_2 \right\}\) es un conjunto ortogonal de vectores. Por otro lado se puede computar eso\( \| \vec{u}_1 \| = \| \vec{u}_2 \| = \sqrt{2} \neq 1\) y así no es un conjunto ortonormal.
Así, para encontrar un conjunto ortonormal correspondiente, simplemente necesitamos normalizar cada vector. Escribiremos\(\{ \vec{w}_1, \vec{w}_2 \}\) para el conjunto ortonormal correspondiente. Entonces,\[\begin{aligned} \vec{w}_1 &= \frac{1}{ \| \vec{u}_1 \| } \vec{u}_1\\ &= \frac{1}{\sqrt{2}} \left[ \begin{array}{c} 1 \\ 1 \end{array} \right] \\ &= \left[ \begin{array}{c} \frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{2}} \end{array} \right]\end{aligned}\]
Del mismo modo,\[\begin{aligned} \vec{w}_2 &= \frac{1}{ \| \vec{u}_2 \| } \vec{u}_2\\ &= \frac{1}{\sqrt{2}} \left[ \begin{array}{r} -1 \\ 1 \end{array} \right] \\ &= \left[ \begin{array}{r} -\frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{2}} \end{array} \right]\end{aligned}\]
Por lo tanto, el conjunto ortonormal correspondiente es\[\left\{ \vec{w}_1, \vec{w}_2 \right\} = \left\{ \left[ \begin{array}{c} \frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{2}} \end{array} \right], \left[ \begin{array}{r} -\frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{2}} \end{array} \right] \right\}\nonumber \]
Se puede verificar que este conjunto es ortogonal.
Considere un conjunto ortogonal de vectores en\(\mathbb{R}^n\), escrito\(\{ \vec{w}_1, \cdots, \vec{w}_k \}\) con\(k \leq n\). El lapso de estos vectores es un subespacio\(W\) de\(\mathbb{R}^n\). Si pudiéramos demostrar que este conjunto ortogonal también es linealmente independiente, tendríamos una base de\(W\). Esto lo mostraremos en el siguiente teorema.
Let\(\{ \vec{w}_1, \vec{w}_2, \cdots, \vec{w}_k \}\) Ser un conjunto ortonormal de vectores en\(\mathbb{R}^n\). Entonces este conjunto es linealmente independiente y forma una base para el subespacio\(W = \mathrm{span} \{ \vec{w}_1, \vec{w}_2, \cdots, \vec{w}_k \}\).
- Prueba
-
Para mostrar que es un conjunto linealmente independiente, supongamos que una combinación lineal de estos vectores es igual\(\vec{0}\), como:\[a_1 \vec{w}_1 + a_2 \vec{w}_2 + \cdots + a_k \vec{w}_k = \vec{0}, a_i \in \mathbb{R}\nonumber \] Necesitamos mostrar que todos\(a_i = 0\). Para ello, toma el producto punto de cada lado de la ecuación anterior con el vector\(\vec{w}_i\) y obtén lo siguiente.
\[\begin{aligned} \vec{w}_i \cdot (a_1 \vec{w}_1 + a_2 \vec{w}_2 + \cdots + a_k \vec{w}_k ) &= \vec{w}_i \cdot \vec{0}\\ a_1 (\vec{w}_i \cdot \vec{w}_1) + a_2 (\vec{w}_i \cdot \vec{w}_2) + \cdots + a_k (\vec{w}_i \cdot \vec{w}_k) &= 0 \end{aligned}\]
Ahora como el conjunto es ortogonal,\(\vec{w}_i \cdot \vec{w}_m = 0\) para todos\(m \neq i\), así tenemos:\[a_1 (0) + \cdots + a_i(\vec{w}_i \cdot \vec{w}_i) + \cdots + a_k (0) = 0\nonumber \]\[a_i \| \vec{w}_i \| ^2 = 0\nonumber \]
Ya que el conjunto es ortogonal, lo sabemos\( \| \vec{w}_i \| ^2 \neq 0\). De ello se deduce que\(a_i =0\). Dado que el\(a_i\) fue elegido arbitrariamente, el conjunto\(\{ \vec{w}_1, \vec{w}_2, \cdots, \vec{w}_k \}\) es linealmente independiente.
Finalmente ya que\(W = \mbox{span} \{ \vec{w}_1, \vec{w}_2, \cdots, \vec{w}_k \}\), el conjunto de vectores también abarca\(W\) y por lo tanto forma una base de\(W\).
Si un conjunto ortogonal es una base para un subespacio, llamamos a esto una base ortogonal. De igual manera, si un conjunto ortonormal es una base, llamamos a esto una base ortonormal.
Concluimos esta sección con una discusión sobre las expansiones de Fourier. Dada cualquier base\(B\) ortogonal\(\mathbb{R}^n\) y un vector arbitrario\(\vec{x} \in \mathbb{R}^n\), ¿cómo expresamos\(\vec{x}\) como una combinación lineal de vectores en\(B\)? La solución es la expansión de Fourier.
Dejar\(V\) ser un subespacio de\(\mathbb{R}^n\) y supongamos que\(\{ \vec{u}_1, \vec{u}_2, \ldots, \vec{u}_m \}\) es una base ortogonal de\(V\). Entonces para cualquier\(\vec{x}\in V\),
\[\vec{x} = \left(\frac{\vec{x}\cdot \vec{u}_1}{ \| \vec{u}_1 \| ^2}\right) \vec{u}_1 + \left(\frac{\vec{x}\cdot \vec{u}_2}{ \| \vec{u}_2 \| ^2}\right) \vec{u}_2 + \cdots + \left(\frac{\vec{x}\cdot \vec{u}_m}{ \| \vec{u}_m \| ^2}\right) \vec{u}_m\nonumber \]
Esta expresión se llama la expansión de Fourier de\(\vec{x}\), y\[\frac{\vec{x}\cdot \vec{u}_j}{ \| \vec{u}_j \| ^2},\nonumber \]\(j=1,2,\ldots,m\) son los coeficientes de Fourier.
Considera el siguiente ejemplo.
Dejar\(\vec{u}_1= \left[\begin{array}{r} 1 \\ -1 \\ 2 \end{array}\right], \vec{u}_2= \left[\begin{array}{r} 0 \\ 2 \\ 1 \end{array}\right]\), y\(\vec{u}_3 =\left[\begin{array}{r} 5 \\ 1 \\ -2 \end{array}\right]\), y dejar\(\vec{x} =\left[\begin{array}{r} 1 \\ 1 \\ 1 \end{array}\right]\).
Entonces\(B=\{ \vec{u}_1, \vec{u}_2, \vec{u}_3\}\) es una base ortogonal de\(\mathbb{R}^3\).
Calcular la expansión de Fourier de\(\vec{x}\), escribiendo así\(\vec{x}\) como una combinación lineal de los vectores de\(B\).
Solución
Ya que\(B\) es una base (verificar!) hay una manera única de expresar\(\vec{x}\) como una combinación lineal de los vectores de\(B\). Por otra parte ya que\(B\) es una base ortogonal (verificar!) , entonces esto se puede hacer calculando la expansión de Fourier de\(\vec{x}\).
Es decir:
\[\vec{x} = \left(\frac{\vec{x}\cdot \vec{u}_1}{ \| \vec{u}_1 \| ^2}\right) \vec{u}_1 + \left(\frac{\vec{x}\cdot \vec{u}_2}{ \| \vec{u}_2 \| ^2}\right) \vec{u}_2 + \left(\frac{\vec{x}\cdot \vec{u}_3}{ \| \vec{u}_3 \| ^2}\right) \vec{u}_3. \nonumber\]
Calculamos fácilmente:
\[\frac{\vec{x}\cdot\vec{u}_1}{ \| \vec{u}_1 \| ^2} = \frac{2}{6}, \; \frac{\vec{x}\cdot\vec{u}_2}{ \| \vec{u}_2 \| ^2} = \frac{3}{5}, \mbox{ and } \frac{\vec{x}\cdot\vec{u}_3}{ \| \vec{u}_3 \| ^2} = \frac{4}{30}. \nonumber\]
Por lo tanto,\[\left[\begin{array}{r} 1 \\ 1 \\ 1 \end{array}\right] = \frac{1}{3}\left[\begin{array}{r} 1 \\ -1 \\ 2 \end{array}\right] +\frac{3}{5}\left[\begin{array}{r} 0 \\ 2 \\ 1 \end{array}\right] +\frac{2}{15}\left[\begin{array}{r} 5 \\ 1 \\ -2 \end{array}\right]. \nonumber\]
Matrices ortogonales
Recordemos que el proceso para encontrar la inversa de una matriz fue a menudo engorroso. En contraste, fue muy fácil tomar la transposición de una matriz. Por suerte para algunas matrices especiales, la transposición es igual a la inversa. Cuando una\(n \times n\) matriz tiene todas las entradas reales y su transposición es igual a su inversa, la matriz se denomina matriz ortogonal.
La definición precisa es la siguiente.
Una\(n\times n\) matriz real\(U\) se llama matriz ortogonal si
\[UU^{T}=U^{T}U=I.\nonumber \]
Nota ya que\(U\) se supone que es una matriz cuadrada, basta con verificar solo una de estas igualdades\(UU^{T}=I\) o\(U^{T}U=I\) retenciones para garantizar que\(U^T\) es la inversa de\(U\).
Considera el siguiente ejemplo.
Matriz ortogonal Mostrar la matriz\[U=\left[ \begin{array}{rr} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \end{array} \right]\nonumber \] es ortogonal.
Solución
Todo lo que tenemos que hacer es verificar (una de las ecuaciones de) los requisitos de Definición\(\PageIndex{7}\).
\[UU^{T}=\left[ \begin{array}{rr} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \end{array} \right] \left[ \begin{array}{rr} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \end{array} \right] = \left[ \begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array} \right]\nonumber \]
Ya que\(UU^{T} = I\), esta matriz es ortogonal.
Aquí hay otro ejemplo.
Matriz ortogonal Let\(U=\left[ \begin{array}{rrr} 1 & 0 & 0 \\ 0 & 0 & -1 \\ 0 & -1 & 0 \end{array} \right] .\) Es\(U\) ortogonal?
Solución
Nuevamente la respuesta es sí y esto se puede verificar simplemente mostrando que\(U^{T}U=I\):
\[\begin{aligned} U^{T}U&=\left[ \begin{array}{rrr} 1 & 0 & 0 \\ 0 & 0 & -1 \\ 0 & -1 & 0 \end{array} \right] ^{T}\left[ \begin{array}{rrr} 1 & 0 & 0 \\ 0 & 0 & -1 \\ 0 & -1 & 0 \end{array} \right] \\ &=\left[ \begin{array}{rrr} 1 & 0 & 0 \\ 0 & 0 & -1 \\ 0 & -1 & 0 \end{array} \right] \left[ \begin{array}{rrr} 1 & 0 & 0 \\ 0 & 0 & -1 \\ 0 & -1 & 0 \end{array} \right] \\ &=\left[ \begin{array}{rrr} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array} \right]\end{aligned}\]
Cuando decimos que\(U\) es ortogonal, estamos diciendo eso\(UU^T=I\), es decir, que\[\sum_{j}u_{ij}u_{jk}^{T}=\sum_{j}u_{ij}u_{kj}=\delta _{ik}\nonumber \] donde\(\delta _{ij}\) está el símbolo de Kronecker definido por\[\delta _{ij}=\left\{ \begin{array}{c} 1 \text{ if }i=j \\ 0\text{ if }i\neq j \end{array} \right.\nonumber \]
En palabras, el producto de la\(i^{th}\) fila de\(U\) con la\(k^{th}\) fila da\(1\) si\(i=k\) y\(0\) si\(i\neq k.\) Lo mismo es cierto de las columnas porque\(U^{T}U=I\) también. Por lo tanto,\[\sum_{j}u_{ij}^{T}u_{jk}=\sum_{j}u_{ji}u_{jk}=\delta _{ik}\nonumber \] que dice que el producto de una columna con otra columna da\(1\) si las dos columnas son iguales y\(0\) si las dos columnas son diferentes.
Más sucintamente, esto establece que si\(\vec{u}_{1},\cdots ,\vec{u}_{n}\) son las columnas de\(U,\) una matriz ortogonal, entonces\[\vec{u}_{i}\cdot \vec{u}_{j}=\delta _{ij} = \left\{ \begin{array}{c} 1\text{ if }i=j \\ 0\text{ if }i\neq j \end{array} \right.\nonumber \]
Diremos que las columnas forman un conjunto ortonormal de vectores, y de manera similar para las filas. Así, una matriz es ortogonal si sus filas (o columnas) forman un conjunto ortonormal de vectores. Observe que la convención es llamar a tal matriz ortogonal en lugar de ortonormal (¡aunque esto puede tener más sentido!).
Las filas de una matriz\(n \times n\) ortogonal forman una base ortonormal de\(\mathbb{R}^n\). Además, cualquier base ortonormal de se\(\mathbb{R}^n\) puede utilizar para construir una matriz\(n \times n\) ortogonal.
- Prueba
-
Recordemos del teorema\(\PageIndex{1}\) que un conjunto ortonormal es linealmente independiente y forma una base para su lapso. Dado que las filas de una matriz\(n \times n\) ortogonal forman un conjunto ortonormal, deben ser linealmente independientes. Ahora tenemos vectores\(n\) linealmente independientes, y de ello se deduce que su lapso es igual\(\mathbb{R}^n\). Por lo tanto, estos vectores forman una base ortonormal para\(\mathbb{R}^n\).
Supongamos ahora que tenemos una base ortonormal para\(\mathbb{R}^n\). Dado que la base contendrá\(n\) vectores, estos pueden ser utilizados para construir una\(n \times n\) matriz, con cada vector convirtiéndose en una fila. Por lo tanto, la matriz está compuesta por filas ortonormales, lo que por nuestra discusión anterior, significa que la matriz es ortogonal. Tenga en cuenta que también podríamos tener construir una matriz con cada vector convirtiéndose en una columna en su lugar, y esto nuevamente sería una matriz ortogonal. De hecho esto es simplemente la transposición de la matriz anterior.
Considera la siguiente proposición.
Det Supongamos\(U\) es una matriz ortogonal. Entonces\(\det \left( U\right) = \pm 1.\)
- Prueba
-
Este resultado se desprende de las propiedades de los determinantes. Recordemos que para cualquier matriz\(A\),\(\det(A)^T = \det(A)\). Ahora si\(U\) es ortogonal, entonces:\[(\det \left( U\right)) ^{2}=\det \left( U^{T}\right) \det \left( U\right) =\det \left( U^{T}U\right) =\det \left( I\right) =1\nonumber \]
Por lo tanto\((\det (U))^2 = 1\) y de ello se deduce\(\det \left( U\right) = \pm 1\).
Las matrices ortogonales se dividen en dos clases, propias e impropias. Las matrices ortogonales adecuadas son aquellas cuyo determinante es igual a 1 y las impropias son aquellas cuyo determinante es igual\(-1\). El motivo de la distinción es que a veces se considera que las matrices ortogonales impropias no tienen significación física. Estas matrices provocan un cambio de orientación que correspondería al paso del material por sí mismo de manera no física. Por lo tanto, al considerar qué sistemas de coordenadas deben considerarse en ciertas aplicaciones, solo es necesario considerar aquellos que están relacionados por una transformación ortogonal adecuada. Geométricamente, las transformaciones lineales determinadas por las matrices ortogonales adecuadas corresponden a la composición de las rotaciones.
Concluimos esta sección con dos propiedades útiles de matrices ortogonales.
Supongamos\(A\) y\(B\) son matrices ortogonales. Entonces\(AB\) y\(A^{-1}\) ambos existen y son ortogonales.
Solución
Primero examinamos el producto\(AB\). \[(AB)(B^TA^T)=A(BB^T)A^T =AA^T=I\nonumber \]Ya que\(AB\) es cuadrada,\(B^TA^T=(AB)^T\) es la inversa de\(AB\), por lo tanto\(AB\) es invertible, y\((AB)^{-1}=(AB)^T\) por lo tanto,\(AB\) es ortogonal.
A continuación mostramos que también\(A^{-1}=A^T\) es ortogonal. \[(A^{-1})^{-1} = A = (A^T)^{T} =(A^{-1})^{T}\nonumber \]Por lo tanto también\(A^{-1}\) es ortogonal.
Proceso Gram-Schmidt
El proceso Gram-Schmidt es un algoritmo para transformar un conjunto de vectores en un conjunto ortonormal que abarca el mismo subespacio, que está generando la misma colección de combinaciones lineales (ver Definición 9.2.2).
El objetivo del proceso Gram-Schmidt es tomar un conjunto linealmente independiente de vectores y transformarlo en un conjunto ortonormal con el mismo lapso. El primer objetivo es construir un conjunto ortogonal de vectores con el mismo lapso, ya que a partir de ahí se puede obtener un conjunto ortonormal simplemente dividiendo cada vector por su longitud.
Let\(\{ \vec{u}_1,\cdots ,\vec{u}_n \}\) Ser un conjunto de vectores linealmente independientes en\(\mathbb{R}^{n}\).
I: Construir un nuevo conjunto de vectores de la\(\{ \vec{v}_1,\cdots ,\vec{v}_n \}\) siguiente manera:\[\begin{array}{ll} \vec{v}_1 & = \vec{u}_1 \\ \vec{v}_{2} & = \vec{u}_{2} - \left( \dfrac{ \vec{u}_2 \cdot \vec{v}_1}{ \| \vec{v}_1 \| ^2} \right) \vec{v}_1\\ \vec{v}_{3} & = \vec{u}_{3} - \left( \dfrac{\vec{u}_3 \cdot \vec{v}_1}{ \| \vec{v}_1 \| ^2} \right) \vec{v}_1 - \left( \dfrac{\vec{u}_3 \cdot \vec{v}_2}{ \| \vec{v}_2 \| ^2} \right) \vec{v}_2\\ \vdots \\ \vec{v}_{n} & = \vec{u}_{n} - \left( \dfrac{\vec{u}_n \cdot \vec{v}_1}{ \| \vec{v}_1 \| ^2} \right) \vec{v}_1 - \left( \dfrac{\vec{u}_n \cdot \vec{v}_2}{ \| \vec{v}_2 \| ^2} \right) \vec{v}_2 - \cdots - \left( \dfrac{\vec{u}_{n} \cdot \vec{v}_{n-1}}{ \| \vec{v}_{n-1} \| ^2} \right) \vec{v}_{n-1} \\ \end{array}\nonumber \]
II: Ahora vamos\(\vec{w}_i = \dfrac{\vec{v}_i}{ \| \vec{v}_i \| }\) por\(i=1, \cdots ,n\).
Entonces
- \(\left\{ \vec{v}_1, \cdots, \vec{v}_n \right\}\)es un conjunto ortogonal.
- \(\left\{ \vec{w}_1,\cdots , \vec{w}_n \right\}\)es un conjunto ortonormal.
- \(\mathrm{span}\left\{ \vec{u}_1,\cdots ,\vec{u}_n \right\} = \mathrm{span} \left\{ \vec{v}_1, \cdots, \vec{v}_n \right\} = \mathrm{span}\left\{ \vec{w}_1,\cdots ,\vec{w}_n \right\}\).
Solución
La prueba completa de este algoritmo está más allá de este material, sin embargo aquí hay una indicación de los argumentos.
Para mostrar que\(\left\{ \vec{v}_1,\cdots , \vec{v}_n \right\}\) es un conjunto ortogonal, vamos\[a_2 = \dfrac{ \vec{u}_2 \cdot \vec{v}_1}{ \| \vec{v}_1 \| ^2}\nonumber \] entonces:\[\begin{array}{ll} \vec{v}_1 \cdot \vec{v}_2 & = \vec{v}_1 \cdot \left( \vec{u}_2 - a_2 \vec{v}_1 \right) \\ & = \vec{v}_1 \cdot \vec{u}_2 - a_2 (\vec{v}_1 \cdot \vec{v}_1 \\ & = \vec{v}_1 \cdot \vec{u}_2 - \dfrac{ \vec{u}_2 \cdot \vec{v}_1}{ \| \vec{v}_1 \| ^2} \| \vec{v}_1 \| ^2 \\ & = ( \vec{v}_1 \cdot \vec{u}_2 ) - ( \vec{u}_2 \cdot \vec{v}_1 ) =0\\ \end{array}\nonumber \] Ahora que has demostrado que\(\{ \vec{v}_1, \vec{v}_2\}\) es ortogonal, usa el mismo método que el anterior para mostrar que también\(\{ \vec{v}_1, \vec{v}_2, \vec{v}_3\}\) es ortogonal, y así sucesivamente.
Entonces de manera similar lo demuestras\(\mathrm{span}\left\{ \vec{u}_1,\cdots ,\vec{u}_n \right\} = \mathrm{span}\left\{ \vec{v}_1,\cdots ,\vec{v}_n \right\}\).
Finalmente definir\(\vec{w}_i = \dfrac{\vec{v}_i}{ \| \vec{v}_i \| }\) for no\(i=1, \cdots ,n\) afecta a la ortogonalidad y produce vectores de longitud 1, de ahí un conjunto ortonormal. También se puede observar que tampoco afecta el lapso y la prueba estaría completa.
Considera el siguiente ejemplo.
Considere el conjunto de vectores\(\{\vec{u}_1, \vec{u}_2\}\) dados como en Ejemplo\(\PageIndex{1}\). Eso es\[\vec{u}_1=\left[ \begin{array}{r} 1 \\ 1 \\ 0 \end{array} \right], \vec{u}_2=\left[ \begin{array}{r} 3 \\ 2 \\ 0 \end{array} \right] \in \mathbb{R}^{3}\nonumber \]
Utilice el algoritmo Gram-Schmidt para encontrar un conjunto ortonormal de vectores\(\{\vec{w}_1, \vec{w}_2\}\) que tengan el mismo lapso.
Solución
Ya remarcamos que el conjunto de vectores en\(\{\vec{u}_1, \vec{u}_2\}\) es linealmente independiente, por lo que podemos proceder con el algoritmo Gram-Schmidt:\[\begin{aligned} \vec{v}_1 &= \vec{u}_1 = \left[ \begin{array}{r} 1 \\ 1 \\ 0 \end{array} \right] \\ \vec{v}_{2} &= \vec{u}_{2} - \left( \dfrac{\vec{u}_2 \cdot \vec{v}_1}{ \| \vec{v}_1 \| ^2} \right) \vec{v}_1\\ &= \left[ \begin{array}{r} 3 \\ 2 \\ 0 \end{array} \right] - \frac{5}{2} \left[ \begin{array}{r} 1 \\ 1 \\ 0 \end{array} \right] \\ &= \left[ \begin{array}{r} \frac{1}{2} \\ - \frac{1}{2} \\ 0 \end{array} \right] \end{aligned}\]
Ahora para normalizar simplemente dejar\[\begin{aligned} \vec{w}_1 &= \frac{\vec{v}_1}{ \| \vec{v}_1 \| } = \left[ \begin{array}{r} \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} \\ 0 \end{array} \right] \\ \vec{w}_2 &= \frac{\vec{v}_2}{ \| \vec{v}_2 \| } = \left[ \begin{array}{r} \frac{1}{\sqrt{2}} \\ - \frac{1}{\sqrt{2}} \\ 0 \end{array} \right]\end{aligned}\]
Se puede verificar que\(\{\vec{w}_1, \vec{w}_2\}\) es un conjunto ortonormal de vectores que tienen el mismo lapso que\(\{\vec{u}_1, \vec{u}_2\}\), a saber, el\(XY\) -plane.
En este ejemplo, comenzamos con un conjunto linealmente independiente y encontramos un conjunto ortonormal de vectores que tenían el mismo lapso. Resulta que si partimos de una base de un subespacio y aplicamos el algoritmo Gram-Schmidt, el resultado será una base ortogonal del mismo subespacio. Esto lo examinamos en el siguiente ejemplo.
Dejar\[\vec{x}_1=\left[\begin{array}{c} 1\\ 0\\ 1\\ 0 \end{array}\right], \vec{x}_2=\left[\begin{array}{c} 1\\ 0\\ 1\\ 1 \end{array}\right], \mbox{ and } \vec{x}_3=\left[\begin{array}{c} 1\\ 1\\ 0\\ 0 \end{array}\right],\nonumber \] y dejar\(U=\mathrm{span}\{\vec{x}_1, \vec{x}_2,\vec{x}_3\}\). Utilice el Proceso Gram-Schmidt para construir una base ortogonal\(B\) de\(U\).
Solución
Primero\(\vec{f}_1=\vec{x}_1\).
Siguiente,\[\vec{f}_2=\left[\begin{array}{c} 1\\ 0\\ 1\\ 1 \end{array}\right] -\frac{2}{2}\left[\begin{array}{c} 1\\ 0\\ 1\\ 0 \end{array}\right] =\left[\begin{array}{c} 0\\ 0\\ 0\\ 1 \end{array}\right].\nonumber \]
Por último,\[\vec{f}_3=\left[\begin{array}{c} 1\\ 1\\ 0\\ 0 \end{array}\right] -\frac{1}{2}\left[\begin{array}{c} 1\\ 0\\ 1\\ 0 \end{array}\right] -\frac{0}{1}\left[\begin{array}{c} 0\\ 0\\ 0\\ 1 \end{array}\right] =\left[\begin{array}{c} 1/2\\ 1\\ -1/2\\ 0 \end{array}\right].\nonumber \]
Por lo tanto,\[\left\{ \left[\begin{array}{c} 1\\ 0\\ 1\\ 0 \end{array}\right], \left[\begin{array}{c} 0\\ 0\\ 0\\ 1 \end{array}\right], \left[\begin{array}{c} 1/2\\ 1\\ -1/2\\ 0 \end{array}\right] \right\}\nonumber \] es una base ortogonal de\(U\). Sin embargo, a veces es más conveniente tratar con vectores que tienen entradas enteras, en cuyo caso tomamos\[B=\left\{ \left[\begin{array}{c} 1\\ 0\\ 1\\ 0 \end{array}\right], \left[\begin{array}{c} 0\\ 0\\ 0\\ 1 \end{array}\right], \left[\begin{array}{r} 1\\ 2\\ -1\\ 0 \end{array}\right] \right\}.\nonumber \]
Proyecciones ortogonales
Un uso importante del Proceso Gram-Schmidt es en las proyecciones ortogonales, el foco de esta sección.
Puede recordar que un subespacio de\(\mathbb{R}^n\) es un conjunto de vectores que contiene el vector cero, y se cierra bajo suma y multiplicación escalar. Llamemos a tal subespacio\(W\). En particular, un plano en el\(\mathbb{R}^n\) que contiene el origen,\(\left(0,0, \cdots, 0 \right)\), es un subespacio de\(\mathbb{R}^n\).
Supongamos que un punto\(Y\) en no\(\mathbb{R}^n\) está contenido en\(W\), entonces ¿a qué punto\(Z\)\(W\) está más cerca\(Y\)? Usando el Proceso Gram-Schmidt, podemos encontrar tal punto. Dejar\(\vec{y}, \vec{z}\) representar los vectores de posición de los puntos\(Y\) y\(Z\) respectivamente, con la\(\vec{y}-\vec{z}\) representación del vector que conecta los dos puntos\(Y\) y\(Z\). De ello se deduce que si\(Z\) es el punto\(W\) más cercano a\(Y\), entonces\(\vec{y} - \vec{z}\) será perpendicular a\(W\) (¿ves por qué?) ; en otras palabras,\(\vec{y} - \vec{z}\) es ortogonal a\(W\) (y a cada vector contenido en\(W\)) como en el siguiente diagrama.
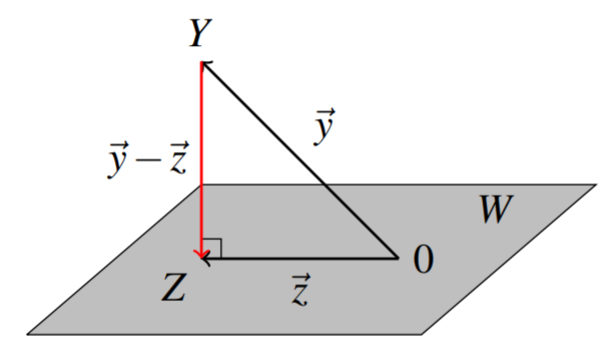
El vector\(\vec{z}\) se llama la proyección ortogonal de\(\vec{y}\) on\(W\). La definición se da de la siguiente manera.
Dejar\(W\) ser un subespacio de\(\mathbb{R}^n\), y\(Y\) ser cualquier punto en\(\mathbb{R}^n\). Entonces la proyección ortogonal de\(Y\) sobre\(W\) está dada por\[\vec{z} = \mathrm{proj}_{W}\left( \vec{y}\right) = \left( \frac{\vec{y} \cdot \vec{w}_1}{ \| \vec{w}_1 \| ^2}\right) \vec{w}_1 + \left( \frac{\vec{y} \cdot \vec{w}_2}{ \| \vec{w}_2 \| ^2}\right) \vec{w}_2 + \cdots + \left( \frac{\vec{y} \cdot \vec{w}_m}{ \| \vec{w}_m \| ^2}\right) \vec{w}_m\nonumber \] donde\(\{\vec{w}_1, \vec{w}_2, \cdots, \vec{w}_m \}\) está cualquier base ortogonal de\(W\).
Por lo tanto, para encontrar la proyección ortogonal, primero debemos encontrar una base ortogonal para el subespacio. Tenga en cuenta que se podría usar una base ortonormal, pero no es necesario en este caso ya que como puede ver arriba la normalización de cada vector se incluye en la fórmula para la proyección.
Antes de explorar esto más a través de un ejemplo, mostramos que la proyección ortogonal de hecho produce un punto\(Z\) (el punto cuyo vector de posición es el vector\(\vec{z}\) anterior) que es el punto\(W\) más cercano a\(Y\).
Dejar\(W\) ser un subespacio de\(\mathbb{R}^n\) y\(Y\) cualquier punto en\(\mathbb{R}^n\). Dejar\(Z\) ser el punto cuyo vector de posición es la proyección ortogonal de\(Y\) sobre\(W\).
Entonces,\(Z\) es el punto\(W\) más cercano a\(Y\).
- Prueba
-
Primero\(Z\) es sin duda un punto en\(W\) ya que está en el lapso de una base de\(W\).
Para demostrar que ese\(Z\) es el punto\(W\) más cercano a\(Y\), queremos mostrar eso\(|\vec{y}-\vec{z}_1| > |\vec{y}-\vec{z}|\) para todos\(\vec{z}_1 \neq \vec{z} \in W\). Empezamos por escribir\(\vec{y}-\vec{z}_1 = (\vec{y} - \vec{z}) + (\vec{z} - \vec{z}_1)\). Ahora, el vector\(\vec{y} - \vec{z}\) es ortogonal a\(W\), y\(\vec{z} - \vec{z}_1\) está contenido en\(W\). Por lo tanto, estos vectores son ortogonales entre sí. Por el Teorema de Pitágoras, tenemos que\[ \| \vec{y} - \vec{z}_1 \| ^2 = \| \vec{y} - \vec{z} \| ^2 + \| \vec{z} -\vec{z}_1 \| ^2 > \| \vec{y} - \vec{z} \| ^2\nonumber \] Esto sigue porque\(\vec{z} \neq \vec{z}_1\) así\( \| \vec{z} -\vec{z}_1 \| ^2 > 0.\)
De ahí,\( \| \vec{y} - \vec{z}_1 \| ^2 > \| \vec{y} - \vec{z} \| ^2\). Tomando la raíz cuadrada de cada lado, obtenemos el resultado deseado.
Considera el siguiente ejemplo.
Dejar\(W\) ser el plano a través del origen dado por la ecuación\(x - 2y + z = 0\). Encuentra el punto\(W\) más cercano al punto\(Y = (1,0,3)\).
Solución
Primero debemos encontrar una base ortogonal para\(W\). Observe que\(W\) se caracteriza por todos los puntos\((a,b,c)\) donde\(c = 2b-a\). En otras palabras,\[W = \left[ \begin{array}{c} a \\ b \\ 2b - a \end{array} \right] = a \left[ \begin{array}{c} 1 \\ 0 \\ -1 \end{array} \right] + b \left[ \begin{array}{c} 0 \\ 1 \\ 2 \end{array} \right], \; a,b \in \mathbb{R}\nonumber \]
Así podemos escribir\(W\) como\[\begin{aligned} W &= \mbox{span} \left\{ \vec{u}_1, \vec{u}_2 \right\} \\ &= \mbox{span} \left\{ \left[ \begin{array}{r} 1 \\ 0 \\ -1 \end{array} \right], \left[ \begin{array}{c} 0 \\ 1 \\ 2 \end{array} \right] \right\}\end{aligned}\]
Observe que este lapso es una base de\(W\) ya que es linealmente independiente. Utilizaremos el Proceso Gram-Schmidt para convertir esto a una base ortogonal,\(\left\{\vec{w}_1, \vec{w}_2 \right\}\). En este caso, como remarcamos sólo es necesario encontrar una base ortogonal, y no se requiere que sea ortonormal.
\[\vec{w}_1 = \vec{u}_1 = \left[ \begin{array}{r} 1 \\ 0 \\ -1 \end{array} \right]\nonumber \]\[\begin{aligned} \vec{w}_2 &= \vec{u}_2 - \left( \frac{ \vec{u}_2 \cdot \vec{w}_1}{ \| \vec{w}_1 \| ^2} \right) \vec{w}_1\\ &= \left[ \begin{array}{c} 0 \\ 1 \\ 2 \end{array} \right] - \left( \frac{-2}{2}\right) \left[ \begin{array}{r} 1 \\ 0 \\ -1 \end{array} \right] \\ &= \left[ \begin{array}{c} 0 \\ 1 \\ 2 \end{array} \right] + \left[ \begin{array}{r} 1 \\ 0 \\ -1 \end{array} \right] \\ &= \left[ \begin{array}{c} 1 \\ 1 \\ 1 \end{array} \right]\end{aligned}\]
Por lo tanto, una base ortogonal de\(W\) es\[\left\{ \vec{w}_1, \vec{w}_2 \right\} = \left\{ \left[ \begin{array}{r} 1 \\ 0 \\ -1 \end{array} \right], \left[ \begin{array}{c} 1 \\ 1 \\ 1 \end{array} \right] \right\}\nonumber \]
Ahora podemos usar esta base para encontrar la proyección ortogonal del punto\(Y=(1,0,3)\) en el subespacio\(W\). Escribiremos el vector\(\vec{y}\) de posición de\(Y\) as\(\vec{y} = \left[ \begin{array}{c} 1 \\ 0 \\ 3 \end{array} \right]\). Usando Definición\(\PageIndex{8}\), calculamos la proyección de la siguiente manera:\[\begin{aligned} \vec{z} &= \mathrm{proj}_{W}\left( \vec{y}\right)\\ &= \left( \frac{\vec{y} \cdot \vec{w}_1}{ \| \vec{w}_1 \| ^2}\right) \vec{w}_1 + \left( \frac{\vec{y} \cdot \vec{w}_2}{ \| \vec{w}_2 \| ^2}\right) \vec{w}_2 \\ &= \left( \frac{-2}{2} \right) \left[ \begin{array}{r} 1 \\ 0 \\ -1 \end{array} \right] + \left( \frac{4}{3} \right) \left[ \begin{array}{c} 1 \\ 1 \\ 1 \end{array} \right] \\ &= \left[ \begin{array}{c} \frac{1}{3} \\ \frac{4}{3} \\ \frac{7}{3} \end{array} \right]\end{aligned}\]
Por lo tanto\(Z\) el punto\(W\) más cercano al punto\((1,0,3)\) es\(\left( \frac{1}{3}, \frac{4}{3}, \frac{7}{3} \right)\).
Recordemos que el vector\(\vec{y} - \vec{z}\) es perpendicular (ortogonal) a todos los vectores contenidos en el plano\(W\). Usando una base para\(W\), de hecho podemos encontrar todos esos vectores que son perpendiculares a\(W\). Llamamos a este conjunto de vectores el complemento ortogonal de\(W\) y lo denotamos\(W^{\perp}\).
Que\(W\) sea un subespacio de\(\mathbb{R}^n\). Entonces el complemento ortogonal de\(W\), escrito\(W^{\perp}\), es el conjunto de todos los vectores\(\vec{x}\) tal que\(\vec{x} \cdot \vec{z} = 0\) para todos los vectores\(\vec{z}\) en\(W\). \[W^{\perp} = \{ \vec{x} \in \mathbb{R}^n \; \mbox{such that} \; \vec{x} \cdot \vec{z} = 0 \; \mbox{for all} \; \vec{z} \in W \}\nonumber \]
El complemento ortogonal se define como el conjunto de todos los vectores que son ortogonales a todos los vectores en el subespacio original. Resulta que es suficiente que los vectores en el complemento ortogonal sean ortogonales a un conjunto de expansión del espacio original.
\(W\)Sea un subespacio de\(\mathbb{R}^n\) tal que\(W = \mathrm{span} \left\{ \vec{w}_1, \vec{w}_2, \cdots, \vec{w}_m \right\}\). Entonces\(W^{\perp}\) es el conjunto de todos los vectores que son ortogonales a cada uno\(\vec{w}_i\) en el conjunto de expansión.
La siguiente proposición demuestra que el complemento ortogonal de un subespacio es en sí mismo un subespacio.
Que\(W\) sea un subespacio de\(\mathbb{R}^n\). Entonces el complemento ortogonal\(W^{\perp}\) es también un subespacio de\(\mathbb{R}^n\).
Considera la siguiente proposición.
El complemento de\(\mathbb{R}^n\) es el conjunto que contiene el vector cero:\[(\mathbb{R}^n)^{\perp} = \left\{ \vec{0} \right\}\nonumber \] Del mismo modo,\[\left\{ \vec{0} \right\}^{\perp} = (\mathbb{R}^n). \nonumber \]
- Prueba
-
Aquí,\(\vec{0}\) es el vector cero de\(\mathbb{R}^n\). Ya que\(\vec{x}\cdot\vec{0}=0\) para todos\(\vec{x}\in\mathbb{R}^n\),\(\mathbb{R}^n\subseteq\{ \vec{0}\}^{\perp}\). Ya que\(\{ \vec{0}\}^{\perp}\subseteq\mathbb{R}^n\), la igualdad sigue, es decir,\(\{ \vec{0}\}^{\perp}=\mathbb{R}^n\).
Nuevamente, ya que\(\vec{x}\cdot\vec{0}=0\) para todos\(\vec{x}\in\mathbb{R}^n\)\(\vec{0}\in (\mathbb{R}^n)^{\perp}\), así\(\{ \vec{0}\}\subseteq(\mathbb{R}^n)^{\perp}\). Supongamos\(\vec{x}\in\mathbb{R}^n\),\(\vec{x}\neq\vec{0}\). Desde\(\vec{x}\cdot\vec{x}=||\vec{x}||^2\) y\(\vec{x}\neq\vec{0}\),\(\vec{x}\cdot\vec{x}\neq 0\), entonces\(\vec{x}\not\in(\mathbb{R}^n)^{\perp}\). Por lo tanto\((\mathbb{R}^n)^{\perp}\subseteq \{\vec{0}\}\), y así\((\mathbb{R}^n)^{\perp}=\{\vec{0}\}\).
En el siguiente ejemplo, veremos cómo encontrar\(W^{\perp}\).
Dejar\(W\) ser el plano a través del origen dado por la ecuación\(x - 2y + z = 0\). Encontrar una base para el complemento ortogonal de\(W\).
Solución
De Ejemplo\(\PageIndex{11}\) sabemos que podemos escribir\(W\) como\[W = \mbox{span} \left\{ \vec{u}_1, \vec{u}_2 \right\} = \mbox{span} \left\{ \left[ \begin{array}{r} 1 \\ 0 \\ -1 \end{array} \right], \left[ \begin{array}{c} 0 \\ 1 \\ 2 \end{array} \right] \right\}\nonumber \]
Para encontrar\(W^{\perp}\), necesitamos encontrar todos los\(\vec{x}\) que son ortogonales a cada vector en este lapso.
Vamos\(\vec{x} = \left[ \begin{array}{c} x_1 \\ x_2 \\ x_3 \end{array} \right]\). Para satisfacer\(\vec{x} \cdot \vec{u}_1 = 0\), se debe mantener la siguiente ecuación. \[x_1 - x_3 = 0\nonumber \]
Para satisfacer\(\vec{x} \cdot \vec{u}_2 = 0\), se debe mantener la siguiente ecuación. \[x_2 + 2x_3 = 0\nonumber \]
Ambas ecuaciones deben ser satisfechas, por lo que tenemos el siguiente sistema de ecuaciones. \[\begin{array}{c} x_1 - x_3 = 0 \\ x_2 + 2x_3 = 0 \end{array}\nonumber \]
Para resolver, configurar la matriz aumentada.
\[\left[ \begin{array}{rrr|r} 1 & 0 & -1 & 0 \\ 0 & 1 & 2 & 0 \end{array} \right]\nonumber \]
Usando la Eliminación Gaussiana, nos encontramos con eso\(W^{\perp} = \mbox{span} \left\{ \left[ \begin{array}{r} 1 \\ -2 \\ 1 \end{array} \right] \right\}\), y por lo tanto\(\left\{ \left[ \begin{array}{r} 1 \\ -2 \\ 1 \end{array} \right] \right\}\) es una base para\(W^{\perp}\).
Los siguientes resultados resumen las propiedades importantes de la proyección ortogonal.
Dejar\(W\) ser un subespacio de\(\mathbb{R}^n\),\(Y\) ser cualquier punto en\(\mathbb{R}^n\), y dejar\(Z\) ser el punto en\(W\) más cercano a\(Y\). Entonces,
- El vector\(\vec{z}\) de posición del punto\(Z\) viene dado por\(\vec{z} = \mathrm{proj}_{W}\left( \vec{y}\right)\)
- \(\vec{z} \in W\)y\(\vec{y} - \vec{z} \in W^{\perp}\)
- \(| Y - Z | < | Y - Z_1 |\)para todos\(Z_1 \neq Z \in W\)
Considera el siguiente ejemplo de este concepto.
Vamos\[\vec{x}_1=\left[\begin{array}{c} 1\\ 0\\ 1\\ 0 \end{array}\right], \vec{x}_2=\left[\begin{array}{c} 1\\ 0\\ 1\\ 1 \end{array}\right], \vec{x}_3=\left[\begin{array}{c} 1\\ 1\\ 0\\ 0 \end{array}\right], \mbox{ and } \vec{v}=\left[\begin{array}{c} 4\\ 3\\ -2\\ 5 \end{array}\right].\nonumber \] Queremos encontrar el vector en el\(W =\mathrm{span}\{\vec{x}_1, \vec{x}_2,\vec{x}_3\}\) más cercano a\(\vec{y}\).
Solución
Primero usaremos el Proceso Gram-Schmidt para construir la base ortogonal,\(B\), de\(W\):\[B=\left\{ \left[\begin{array}{c} 1\\ 0\\ 1\\ 0 \end{array}\right], \left[\begin{array}{c} 0\\ 0\\ 0\\ 1 \end{array}\right], \left[\begin{array}{r} 1\\ 2\\ -1\\ 0 \end{array}\right] \right\}.\nonumber \]
Por teorema\(\PageIndex{4}\),\[\mathrm{proj}_U(\vec{v}) = \frac{2}{2} \left[\begin{array}{c} 1\\ 0\\ 1\\ 0 \end{array}\right] + \frac{5}{1}\left[\begin{array}{c} 0\\ 0\\ 0\\ 1 \end{array}\right] + \frac{12}{6}\left[\begin{array}{r} 1\\ 2\\ -1\\ 0 \end{array}\right] = \left[\begin{array}{r} 3\\ 4\\ -1\\ 5 \end{array}\right]\nonumber \] es el vector\(U\) más cercano a\(\vec{y}\).
Consideremos el siguiente ejemplo.
Que\(W\) sea un subespacio dado por\(W = \mbox{span} \left\{ \left[ \begin{array}{c} 1 \\ 0 \\ 1 \\ 0 \\ \end{array} \right], \left[ \begin{array}{c} 0 \\ 1 \\ 0 \\ 2 \\ \end{array} \right] \right\}\), y\(Y = (1,2,3,4)\).
Encuentra el punto\(Z\)\(W\) más cercano a\(Y\), y además escribe\(\vec{y}\) como la suma de un vector en\(W\) y un vector en\(W^{\perp}\).
Solución
Del teorema\(\PageIndex{3}\) el punto\(Z\) en\(W\) más cercano a\(Y\) está dado por\(\vec{z} = \mathrm{proj}_{W}\left( \vec{y}\right)\).
Observe que dado que los vectores anteriores ya dan una base ortogonal para\(W\), tenemos:
\[\begin{aligned} \vec{z} &= \mathrm{proj}_{W}\left( \vec{y}\right)\\ &= \left( \frac{\vec{y} \cdot \vec{w}_1}{ \| \vec{w}_1 \| ^2}\right) \vec{w}_1 + \left( \frac{\vec{y} \cdot \vec{w}_2}{ \| \vec{w}_2 \| ^2}\right) \vec{w}_2 \\ &= \left( \frac{4}{2} \right) \left[ \begin{array}{c} 1 \\ 0 \\ 1 \\ 0 \end{array} \right] + \left( \frac{10}{5} \right) \left[ \begin{array}{c} 0 \\ 1 \\ 0 \\ 2 \end{array} \right] \\ &= \left[ \begin{array}{c} 2 \\ 2 \\ 2 \\ 4 \end{array} \right]\end{aligned}\]
Por lo tanto el punto\(W\) más cercano a\(Y\) es\(Z = (2,2,2,4)\).
Ahora, necesitamos escribir\(\vec{y}\) como la suma de un vector en\(W\) y un vector en\(W^{\perp}\). Esto se puede hacer fácilmente de la siguiente manera:\[\vec{y} = \vec{z} + (\vec{y} - \vec{z})\nonumber \] ya que\(\vec{z}\) está en\(W\) y como hemos visto\(\vec{y} - \vec{z}\) está en\(W^{\perp}\).
El vector\(\vec{y} - \vec{z}\) viene dado por\[\vec{y} - \vec{z} = \left[ \begin{array}{c} 1 \\ 2 \\ 3 \\ 4 \end{array} \right] - \left[ \begin{array}{c} 2 \\ 2 \\ 2 \\ 4 \end{array} \right] = \left[ \begin{array}{r} -1 \\ 0 \\ 1 \\ 0 \end{array} \right]\nonumber \] Por lo tanto, podemos escribir\(\vec{y}\) como\[\left[ \begin{array}{c} 1 \\ 2 \\ 3 \\ 4 \end{array} \right] = \left[ \begin{array}{c} 2 \\ 2 \\ 2 \\ 4 \end{array} \right] + \left[ \begin{array}{r} -1 \\ 0 \\ 1 \\ 0 \end{array} \right]\nonumber \]
Encuentra el punto\(Z\) en el plano\(3x+y-2z=0\) que está más cerca del punto\(Y=(1,1,1)\).
Solución
La solución procederá de la siguiente manera.
- Encontrar una base\(X\) del subespacio\(W\) de\(\mathbb{R}^3\) definido por la ecuación\(3x+y-2z=0\).
- Ortogonalizar la base\(X\) para obtener una base ortogonal\(B\) de\(W\).
- Encuentra la proyección sobre\(W\) del vector de posición del punto\(Y\).
Ahora comenzamos la solución.
- \(3x+y-2z=0\)es un sistema de una ecuación en tres variables. Poner la matriz aumentada en forma de fila-escalón reducido:\[\left[\begin{array}{rrr|r} 3 & 1 & -2 & 0 \end{array}\right] \rightarrow \left[\begin{array}{rrr|r} 1 & \frac{1}{3} & -\frac{2}{3} & 0 \end{array}\right]\nonumber \] da solución general\(x=\frac{1}{3}s+\frac{2}{3}t\),\(y=s\),\(z=t\) para cualquier\(s,t\in\mathbb{R}\). Entonces\[W=\mathrm{span} \left\{ \left[\begin{array}{r} -\frac{1}{3} \\ 1 \\ 0 \end{array}\right], \left[\begin{array}{r} \frac{2}{3} \\ 0 \\ 1 \end{array}\right]\right\}\nonumber \] vamos\(X=\left\{ \left[\begin{array}{r} -1 \\ 3 \\ 0 \end{array}\right], \left[\begin{array}{r} 2 \\ 0 \\ 3 \end{array}\right]\right\}\). Entonces\(X\) es linealmente independiente y\(\mathrm{span}(X)=W\), así\(X\) es una base de\(W\).
- Utilice el Proceso Gram-Schmidt para obtener una base ortogonal de\(W\):\[\vec{f}_1=\left[\begin{array}{r} -1\\3\\0\end{array}\right]\mbox{ and }\vec{f}_2=\left[\begin{array}{r}2\\0\\3\end{array}\right]-\frac{-2}{10}\left[\begin{array}{r}-1\\3\\0\end{array}\right]=\frac{1}{5}\left[\begin{array}{r}9\\3\\15\end{array}\right].\nonumber\] Por lo tanto,\(B=\left\{\left[\begin{array}{r}-1\\3\\0\end{array}\right], \left[\begin{array}{r}3\\1\\5 \end{array}\right]\right\}\) es una base ortogonal de\(W\).
- Para encontrar el punto\(W\) más cercano\(Z\) a\(Y=(1,1,1)\), computar\[\begin{aligned} \mathrm{proj}_{W}\left[\begin{array}{r} 1 \\ 1 \\ 1 \end{array}\right] & = \frac{2}{10} \left[\begin{array}{r} -1 \\ 3 \\ 0 \end{array}\right] + \frac{9}{35}\left[\begin{array}{r} 3 \\ 1 \\ 5 \end{array}\right]\\ & = \frac{1}{7}\left[\begin{array}{r} 4 \\ 6 \\ 9 \end{array}\right].\end{aligned}\] Por lo tanto,\(Z=\left( \frac{4}{7}, \frac{6}{7}, \frac{9}{7}\right)\).
Aproximación de mínimos cuadrados
No debería sorprender escuchar que muchos problemas no tienen una solución perfecta, y en estos casos el objetivo siempre es tratar de hacer lo mejor posible. Por ejemplo, ¿qué se hace si no hay soluciones a un sistema de ecuaciones lineales\(A\vec{x}=\vec{b}\)? Resulta que lo que hacemos es encontrar\(\vec{x}\) tal que\(A\vec{x}\) esté lo más cerca\(\vec{b}\) posible. Una técnica muy importante que se desprende de las proyecciones ortogonales es la de la aproximación de mínimos cuadrados, y nos permite hacer exactamente eso.
Comenzamos con un lema.
Recordemos que podemos formar la imagen de una\(m \times n\) matriz\(A\) por\(\mathrm{im}\left( A\right) = = \left\{ A\vec{x} : \vec{x} \in \mathbb{R}^n \right\}\). El teorema de reformulación\(\PageIndex{4}\) usando el subespacio\(W=\mathrm{im}\left( A\right)\) da la equivalencia de una condición de ortogonalidad con una condición de minimización. La siguiente imagen ilustra esta condición de ortogonalidad y significado geométrico de este teorema.
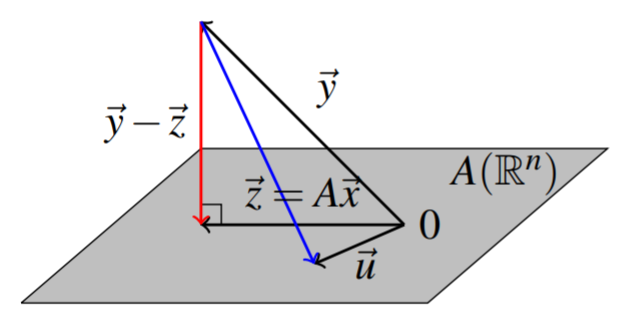
Dejar\(\vec{y}\in \mathbb{R}^{m}\) y dejar\(A\) ser una\(m\times n\) matriz.
Elegir\(\vec{z}\in W= \mathrm{im}\left( A\right)\) dado por\(\vec{z} = \mathrm{proj}_{W}\left( \vec{y}\right)\), y dejar que\(\vec{x} \in \mathbb{R}^{n}\) tal que\(\vec{z}=A\vec{x}\).
Entonces
- \(\vec{y} - A\vec{x} \in W^{\perp}\)
- \( \| \vec{y} - A\vec{x} \| < \| \vec{y} - \vec{u} \| \)para todos\(\vec{u} \neq \vec{z} \in W\)
Observamos una observación sencilla pero útil.
\(A\)Déjese ser una\(m\times n\) matriz. Entonces\[A\vec{x} \cdot \vec{y} = \vec{x}\cdot A^T\vec{y}\nonumber \]
- Prueba
-
Esto se desprende de las definiciones:\[A\vec{x} \cdot \vec{y}=\sum_{i,j}a_{ij}x_{j} y_{i} =\sum_{i,j}x_{j} a_{ji} y_{i}= \vec{x} \cdot A^T\vec{y}\nonumber \]
El siguiente corolario da la técnica de mínimos cuadrados.
Un valor específico del\(\vec{x}\) cual resuelve el problema del Teorema\(\PageIndex{5}\) se obtiene resolviendo la ecuación.\[A^TA\vec{x}=A^T\vec{y}\nonumber \] Además, siempre existe una solución a este sistema de ecuaciones.
- Prueba
-
Para\(\vec{x}\) el minimizador del Teorema\(\PageIndex{5}\),\(\left( \vec{y}-A\vec{x}\right) \cdot A \vec{u} =0\) para todos\(\vec{u} \in \mathbb{R}^{n}\) y desde Lema\(\PageIndex{1}\), esto es lo mismo que decir\[A^T\left( \vec{y}-A\vec{x}\right) \cdot \vec{u}=0\nonumber \] para todos\(u \in \mathbb{R}^{n}.\) Esto implica\[A^T\vec{y}-A^TA\vec{x}=\vec{0}.\nonumber \] Por lo tanto, hay una solución a la ecuación de este corolario, y resuelve el problema de minimización del Teorema\(\PageIndex{5}\).
Tenga en cuenta que\(\vec{x}\) podría no ser único pero\(A\vec{x}\), el punto más cercano de\(A\left(\mathbb{R}^{n}\right)\) a\(\vec{y}\) es único como se mostró en el argumento anterior.
Considera el siguiente ejemplo.
Encuentre una solución de mínimos cuadrados para el sistema\[\left[ \begin{array}{rr} 2 & 1 \\ -1 & 3 \\ 4 & 5 \end{array} \right] \left[ \begin{array}{c} x \\ y \end{array} \right] =\left[ \begin{array}{c} 2 \\ 1 \\ 1 \end{array} \right]\nonumber \]
Solución
Primero, considere si existe una solución real. Para ello, configurar la matriz aumentada dada por\[\left[ \begin{array}{rr|r} 2 & 1 & 2 \\ -1 & 3 & 1 \\ 4 & 5 & 1 \end{array} \right]\nonumber \] La forma reducida fila-escalón de esta matriz aumentada es\[\left[ \begin{array}{rr|r} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array} \right]\nonumber \]
De ello se deduce que no hay una solución real a este sistema. Por lo tanto deseamos encontrar la solución de mínimos cuadrados. Las ecuaciones normales son\[\begin{aligned} A^T A \vec{x} &= A^T \vec{y} \\ \left[ \begin{array}{rrr} 2 & -1 & 4 \\ 1 & 3 & 5 \end{array} \right] \left[ \begin{array}{rr} 2 & 1 \\ -1 & 3 \\ 4 & 5 \end{array} \right] \left[ \begin{array}{c} x \\ y \end{array} \right] &=\left[ \begin{array}{rrr} 2 & -1 & 4 \\ 1 & 3 & 5 \end{array} \right] \left[ \begin{array}{c} 2 \\ 1 \\ 1 \end{array} \right]\end{aligned}\] y así necesitamos resolver el sistema\[\left[ \begin{array}{rr} 21 & 19 \\ 19 & 35 \end{array} \right] \left[ \begin{array}{c} x \\ y \end{array} \right] =\left[ \begin{array}{r} 7 \\ 10 \end{array} \right]\nonumber \] Este es un ejercicio familiar y la solución es\[\left[ \begin{array}{c} x \\ y \end{array} \right] =\left[ \begin{array}{c} \frac{5}{34} \\ \frac{7}{34} \end{array} \right]\nonumber \]
Considera otro ejemplo.
Encuentre una solución de mínimos cuadrados para el sistema\[\left[ \begin{array}{rr} 2 & 1 \\ -1 & 3 \\ 4 & 5 \end{array} \right] \left[ \begin{array}{c} x \\ y \end{array} \right] =\left[ \begin{array}{c} 3 \\ 2 \\ 9 \end{array} \right]\nonumber \]
Solución
Primero, considere si existe una solución real. Para ello, configurar la matriz aumentada dada por\[\left[ \begin{array}{rr|r} 2 & 1 & 3 \\ -1 & 3 & 2 \\ 4 & 5 & 9 \end{array} \right]\nonumber\] La forma reducida fila-escalón de esta matriz aumentada es\[\left[ \begin{array}{rr|r} 1 & 0 & 1 \\ 0 & 1 & 1 \\ 0 & 0 & 0 \end{array} \right]\nonumber \]
De ello se deduce que el sistema tiene una solución dada por\(x=y=1\). Sin embargo, también podemos usar las ecuaciones normales y encontrar la solución de mínimos cuadrados. \[\left[ \begin{array}{rrr} 2 & -1 & 4 \\ 1 & 3 & 5 \end{array} \right] \left[ \begin{array}{rr} 2 & 1 \\ -1 & 3 \\ 4 & 5 \end{array} \right] \left[ \begin{array}{c} x \\ y \end{array} \right] =\left[ \begin{array}{rrr} 2 & -1 & 4 \\ 1 & 3 & 5 \end{array} \right] \left[ \begin{array}{r} 3 \\ 2 \\ 9 \end{array} \right]\nonumber \]Entonces\[\left[ \begin{array}{rr} 21 & 19 \\ 19 & 35 \end{array} \right] \left[ \begin{array}{c} x \\ y \end{array} \right] =\left[ \begin{array}{c} 40 \\ 54 \end{array} \right]\nonumber \]
La solución de mínimos cuadrados es la\[\left[ \begin{array}{c} x \\ y \end{array} \right] =\left[ \begin{array}{c} 1 \\ 1 \end{array} \right]\nonumber \] que es la misma que la solución encontrada anteriormente.
Una aplicación importante del Corolario\(\PageIndex{1}\) es el problema de encontrar la línea de regresión de mínimos cuadrados en la estadística. Supongamos que se le dan puntos en el\(xy\) plano\[\left\{ \left( x_{1},y_{1}\right), \left( x_{2},y_{2}\right), \cdots, \left( x_{n},y_{n}\right) \right\}\nonumber \] y le gustaría encontrar constantes\(m\) y\(b\) tales que la línea\(\vec{y}=m\vec{x}+b\) pase por todos estos puntos. Por supuesto esto será imposible en general. Por lo tanto, tratamos de encontrar\(m,b\) tal que la línea esté lo más cerca posible. El sistema deseado es
\[\left[ \begin{array}{c} y_{1} \\ \vdots \\ y_{n} \end{array} \right] =\left[ \begin{array}{cc} x_{1} & 1 \\ \vdots & \vdots \\ x_{n} & 1 \end{array} \right] \left[ \begin{array}{c} m \\ b \end{array} \right]\nonumber \]
que es de la forma\(\vec{y}=A\vec{x}\). Se desea elegir\(m\) y\(b\) hacer
\[\left \| A\left[ \begin{array}{c} m \\ b \end{array} \right] -\left[ \begin{array}{c} y_{1} \\ \vdots \\ y_{n} \end{array} \right] \right \| ^{2}\nonumber \]
lo más pequeño posible. Según Teorema\(\PageIndex{5}\) y Corolario\(\PageIndex{1}\), los mejores valores para\(m\) y\(b\) ocurren como la solución para
\[A^{T}A\left[ \begin{array}{c} m \\ b \end{array} \right] =A^{T}\left[ \begin{array}{c} y_{1} \\ \vdots \\ y_{n} \end{array} \right] ,\ \;\mbox{where}\; A=\left[ \begin{array}{cc} x_{1} & 1 \\ \vdots & \vdots \\ x_{n} & 1 \end{array} \right]\nonumber \]
Por lo tanto, la computación\(A^{T}A,\)
\[\left[ \begin{array}{cc} \sum_{i=1}^{n}x_{i}^{2} & \sum_{i=1}^{n}x_{i} \\ \sum_{i=1}^{n}x_{i} & n \end{array} \right] \left[ \begin{array}{c} m \\ b \end{array} \right] =\left[ \begin{array}{c} \sum_{i=1}^{n}x_{i}y_{i} \\ \sum_{i=1}^{n}y_{i} \end{array} \right]\nonumber \]
Resolver este sistema de ecuaciones para\(m\) y\(b\) (usando la regla de Cramer, por ejemplo) rinde:
\[m= \frac{-\left( \sum_{i=1}^{n}x_{i}\right) \left( \sum_{i=1}^{n}y_{i}\right) +\left( \sum_{i=1}^{n}x_{i}y_{i}\right) n}{\left( \sum_{i=1}^{n}x_{i}^{2}\right) n-\left( \sum_{i=1}^{n}x_{i}\right) ^{2}}\nonumber \]y\[b=\frac{-\left( \sum_{i=1}^{n}x_{i}\right) \sum_{i=1}^{n}x_{i}y_{i}+\left( \sum_{i=1}^{n}y_{i}\right) \sum_{i=1}^{n}x_{i}^{2}}{\left( \sum_{i=1}^{n}x_{i}^{2}\right) n-\left( \sum_{i=1}^{n}x_{i}\right) ^{2}}.\nonumber \]
Considera el siguiente ejemplo.
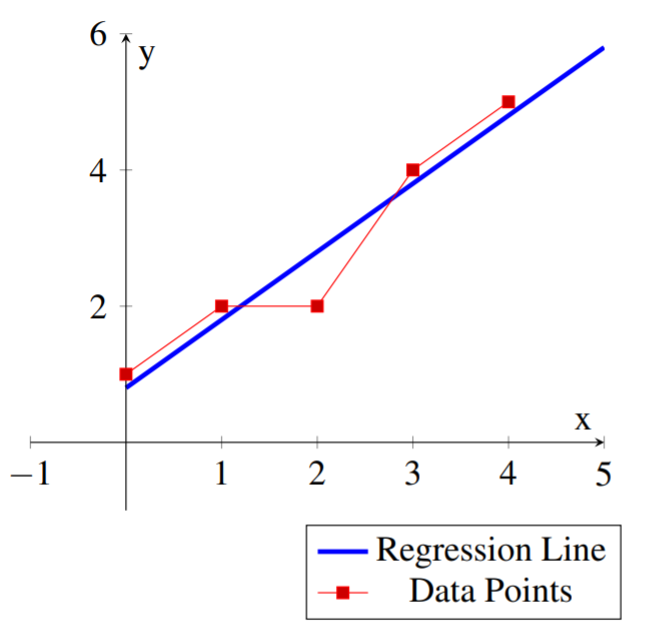
Encuentre la línea de regresión de mínimos cuadrados\(\vec{y}=m\vec{x}+b\) para el siguiente conjunto de puntos de datos:\[\left\{ (0,1), (1,2), (2,2), (3,4), (4,5) \right\} \nonumber\]
Solución
En este caso tenemos puntos de\(n=5\) datos y obtenemos:\[\begin{array}{ll} \sum_{i=1}^{5}x_{i} = 10 & \sum_{i=1}^{5}y_{i} = 14 \\ \\ \sum_{i=1}^{5}x_{i}y_{i} = 38 & \sum_{i=1}^{5}x_{i}^{2} = 30\\ \end{array}\nonumber \] y por lo tanto\[\begin{aligned} m &= \frac{- 10 * 14 + 5*38}{5*30-10^2} = 1.00 \\ \\ b &= \frac{- 10 * 38 + 14*30}{5*30-10^2} = 0.80 \\\end{aligned}\]
La línea de regresión de mínimos cuadrados para el conjunto de puntos de datos es:\[\vec{y} = \vec{x}+.8\nonumber \]
Se podría usar esta línea para aproximar otros valores para los datos. Por ejemplo para\(x=6\) uno se podría utilizar\(y(6)=6+.8=6.8\) como un valor aproximado para los datos.
El siguiente diagrama muestra los puntos de datos y la línea de regresión correspondiente.
Claramente se podría hacer un ajuste de mínimos cuadrados para curvas de la forma\(y=ax^{2}+bx+c\) de la misma manera. En este caso se quiere resolver lo mejor posible para\(a,b,\) y\(c\) el sistema\[\left[ \begin{array}{ccc} x_{1}^{2} & x_{1} & 1 \\ \vdots & \vdots & \vdots \\ x_{n}^{2} & x_{n} & 1 \end{array} \right] \left[ \begin{array}{c} a \\ b \\ c \end{array} \right] =\left[ \begin{array}{c} y_{1} \\ \vdots \\ y_{n} \end{array} \right]\nonumber \] y uno utilizaría la misma técnica anterior. Muchos otros problemas similares son importantes, incluyendo muchos en dimensiones superiores y todos se resuelven de la misma manera.