4.12: Aplicaciones
- Page ID
- 114538
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Aplicaciones
- Aplicar los conceptos de vectores en\(\mathbb{R}^n\) las aplicaciones de la física y el trabajo.
Vectores y Física
Supongamos que empujas algo. Entonces, tu empuje se compone de dos componentes, qué tan fuerte empujas y la dirección en la que empujas. Esto ilustra el concepto de fuerza.
La fuerza es un vector. La magnitud de este vector es una medida de lo duro que está empujando. Se mide en unidades como Newtons o libras o toneladas. La dirección de este vector es la dirección en la que se está produciendo el empuje.
Los vectores se utilizan para modelar la fuerza y otros vectores físicos como la velocidad. Al igual que con todos los vectores, una fuerza de modelado vectorial tiene dos ingredientes esenciales, su magnitud y su dirección.
Recordemos los vectores especiales que apuntan a lo largo de los ejes de coordenadas. Estos vienen dados por\[\vec{e}_{i} = \left [ 0 \cdots 0 \; 1 \; 0 \cdots 0 \right ]^T\nonumber \] donde\(1\) está el en la\(i^{th}\) ranura y hay ceros en todos los demás espacios. La dirección de\(\vec{e}_{i}\) se conoce como la\(i^{th}\) dirección.
Consideremos la siguiente imagen que ilustra el caso de\(\mathbb{R}^{3}.\) Recordemos que en\(\mathbb{R}^3\), podemos referirnos a estos vectores como\(\vec{i}, \vec{j},\) y\(\vec{k}\).
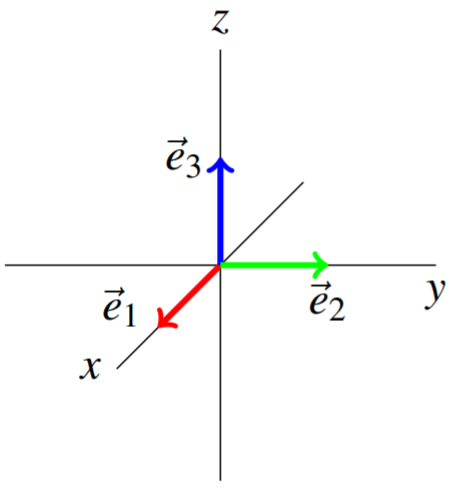
Dado un vector\(\vec{u}=\left [ u_{1} \cdots u_{n}\right ]^T ,\) se deduce que\[\vec{u}=u_{1}\vec{e}_{1}+\cdots +u_{n}\vec{e}_{n}= \sum_{k=1}^{n}u_{i}\vec{e}_{i}\nonumber \]
¿Qué significa físicamente la adición de vectores? Supongamos que se aplican dos fuerzas a algún objeto. Cada uno de estos estaría representado por un vector de fuerza y las dos fuerzas que actúan juntas producirían una fuerza global que actuaría sobre el objeto que también sería un vector de fuerza conocido como el resultante. Supongamos que los dos vectores son\(\vec{u}=\sum_{k=1}^{n}u_{i}\vec{e}_{i}\) y\(\vec{v}=\sum_{k=1}^{n}v_{i}\vec{e}_{i}\). Entonces el vector\(\vec{u}\) involucra un componente en la\(i^{th}\) dirección dada por\(u_{i}\vec{e}_{i}\), mientras que el componente en la\(i^{th}\) dirección de\(\vec{v}\) es\(v_{i}\vec{e}_{i}.\) Entonces el vector\(\vec{u} + \vec{v}\) debe tener un componente en la\(i^{th}\) dirección igual a\(\left( u_{i}+v_{i}\right) \vec{e}_{i}.\) Esto es exactamente lo que es se obtienen cuando los vectores,\(\vec{u}\) y\(\vec{v}\) se agregan. \[\begin{aligned} \vec{u}+\vec{v}& =\left [ u_{1}+v_{1} \cdots u_{n}+v_{n}\right ]^T \\ & =\sum_{i=1}^{n}\left( u_{i}+v_{i}\right) \vec{e}_{i}\end{aligned}\]
Así, la adición de vectores de acuerdo a las reglas de adición en las\(\mathbb{R }^{n}\) que se presentaron anteriormente, produce el vector apropiado que duplica el efecto acumulativo de todos los vectores en la suma.
Consideremos ahora algunos ejemplos de adición de vectores.
Hay tres cuerdas adheridas a un automóvil y tres personas tiran de estas cuerdas. El primero ejerce una fuerza de\(\vec{F}_1 = 2\vec{i} + 3\vec{j} -2 \vec{k}\) Newtons, el segundo ejerce una fuerza de\(\vec{F}_2 = 3\vec{i}+5\vec{j}+\vec{k}\) Newtons y el tercero ejerce una fuerza de\(5\vec{i}-\vec{j}+2\vec{k}\) Newtons. Encuentra la fuerza total en la dirección de\(\vec{i}\).
Solución
Para encontrar la fuerza total, agregamos los vectores como se describió anteriormente. Esto lo da Por\[\begin{aligned} &(2\vec{i}+3\vec{j}-2\vec{k}) + (3\vec{i}+5\vec{j}+\vec{k}) + (5\vec{i}-\vec{j}+2\vec{k})\\ &= (2 + 3 + 5) \vec{i} + (3 + 5 + -1) \vec{j} + (-2+1+2) \vec{k} \\ &= 10 \vec{i} + 7 \vec{j} + \vec{k}\end{aligned}\] lo tanto, la fuerza total es\(10\vec{i}+7\vec{j}+\vec{k}\) Newtons. Por lo tanto, la fuerza en la\(\vec{i}\) dirección es\(10\) Newtons.
Considera otro ejemplo.
Un avión vuela el noreste a 100 millas por hora. Escribe esto como un vector.
Solución
Sigue una imagen de esta situación.
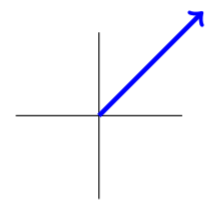
Por lo tanto, necesitamos encontrar el vector\(\vec{u}\) que tiene longitud 100 y dirección como se muestra en este diagrama. Podemos considerar el vector\(\vec{u}\) como la hipotenusa de un triángulo rectángulo que tiene lados iguales, ya que la dirección de\(\vec{u}\) corresponde con la\(45 ^{\circ}\) línea. Los lados, correspondientes a las\(\vec{j}\) direcciones\(\vec{i}\) y, deben ser cada uno de longitud 100/\(\sqrt{2}.\) Por lo tanto, el vector viene dado por\[\vec{u} = \frac{100}{\sqrt{2}} \vec{i}+ \frac{100}{\sqrt{2 }}\vec{j} = \left [ \begin{array}{rr} {0.05in} \frac{100}{\sqrt{2}} & {0.05in}\frac{100}{\sqrt{2}} \end{array} \right ]^T \nonumber \]
Este ejemplo también motiva el concepto de velocidad, definido a continuación.
La velocidad de un objeto es una medida de lo rápido que va. Se mide en unidades de longitud por unidad de tiempo. Por ejemplo, millas por hora, kilómetros por minuto, pies por segundo. La velocidad es un vector que tiene la velocidad como la magnitud pero que también especifica la dirección.
Así el vector de velocidad en el ejemplo anterior es\( {0.05in}\frac{100}{\sqrt{2}}\vec{i}+ {0.05in}\frac{100}{\sqrt{2}}\vec{j}\), mientras que la velocidad es\(100\) millas por hora.
Considera el siguiente ejemplo.
La velocidad de un avión se\(100\vec{i}+\vec{j}+\vec{k}\) mide en kilómetros por hora y en cierto instante su posición es\(\left( 1,2,1\right) .\)
Encuentra la posición de este avión un minuto después.
Solución
Aquí imagina un sistema de coordenadas cartesianas en el que el tercer componente es la altitud y el primer y segundo componentes se miden en una línea de Oeste a Este y una línea de Sur a Norte.
Considere el vector\(\left [ \begin{array}{rrr} 1 & 2 & 1 \end{array} \right ]^T ,\) que es el vector de posición inicial del avión. A medida que el plano se mueve, el vector de posición cambia de acuerdo con el vector de velocidad. Después de un minuto (considerado a partir\(\frac{1}{60}\) de una hora) el avión se ha movido en\(\vec{i}\) dirección a una distancia de\(100\times \frac{1}{60}= \frac{5}{3}\) kilómetro. En la\(\vec{j}\) dirección se ha movido\(\frac{1}{60}\) kilómetro durante este mismo tiempo, mientras que se mueve\(\frac{1}{60}\) kilómetro en\(\vec{k}\) dirección. Por lo tanto, el nuevo vector de desplazamiento para el avión es\[\left [ \begin{array}{rrr} 1 & 2 & 1 \end{array} \right ]^T + \left [ \begin{array}{rrr} \frac{5}{3} & \frac{1}{60} & \frac{1}{60} \end{array} \right ]^T =\left [ \begin{array}{rrr} \frac{8}{3} & \frac{121}{60} & \frac{121}{60} \end{array} \right ]^T\nonumber \]
Consideremos ahora un ejemplo que implica combinar dos velocidades.
Cierto río tiene medio kilómetro de ancho con una corriente que fluye a 4 kilómetros por hora de Este a Oeste. Un hombre nada directamente hacia la orilla opuesta a la orilla sur del río a una velocidad de 3 kilómetros por hora. ¿A qué distancia del río se encuentra cuando ha nadado a través de él? ¿Hasta dónde termina nadando?
Solución
Considera el siguiente cuadro que demuestra el escenario anterior.
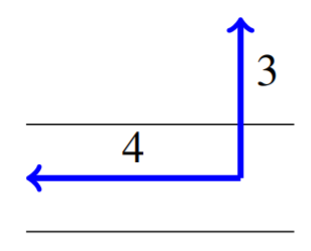
Primero queremos saber el tiempo total de la natación al otro lado del río. La velocidad en la dirección a través del río es de\(3\) kilómetros por hora, y el río es de\(\frac{1}{2}\) kilómetro de ancho. Sigue que el viaje toma\(1/6\) hora o\(10\) minutos.
Ahora, podemos calcular hasta qué punto aguas abajo va a terminar. Dado que el río corre a un ritmo de\(4\) kilómetros por hora, y el viaje dura\(1/6\) hora, la distancia recorrida río abajo viene dada por\(4 \left(\frac{1}{6}\right) = \frac{2}{3}\) kilómetros.
La distancia recorrida por el nadador viene dada por la hipotenusa de un triángulo rectángulo. Los dos brazos del triángulo están dados por la distancia a través del río,\(\frac{1}{2}\) km, y la distancia recorrida río abajo,\(\frac{2}{3}\) km. Entonces, utilizando el Teorema de Pitágoras, podemos calcular la distancia total\(d\) recorrida. \[d = \sqrt{ \left(\frac{2}{3} \right)^2 + \left( \frac{1}{2} \right) ^2 } = \frac{5}{6} \mbox{km}\nonumber \]
Por lo tanto, el nadador recorre una distancia total de\(\frac{5}{6}\) kilómetros.
Trabajo
El concepto matemático de trabajo es una aplicación de vectores en\(\mathbb{R}^n\). El concepto físico de trabajo difiere de la noción de trabajo empleada en la conversación ordinaria. Por ejemplo, supongamos que debía deslizar un peso de 150 libras de una mesa que mide tres pies de altura y barajar a lo largo del piso por 50 yardas, manteniendo la altura siempre tres pies y luego depositar este peso en otra mesa de tres pies de altura. El concepto físico de trabajo indicaría que la fuerza ejercida por tus brazos no funcionó durante este proyecto. El motivo de esta definición es que a pesar de que tus brazos ejercían una fuerza considerable sobre el peso, la dirección del movimiento estaba en ángulo recto con la fuerza que ejercían. La única parte de una fuerza que sí funciona en el sentido de la física es el componente de la fuerza en la dirección del movimiento.
El trabajo se define como la magnitud del componente de esta fuerza multiplicado por la distancia sobre la que actúa, cuando el componente de fuerza apunta en la dirección del movimiento. En el caso donde la fuerza apunta exactamente en la dirección opuesta del movimiento el trabajo viene dado por\(\left( -1\right)\) veces la magnitud de este componente por la distancia. Así, el trabajo realizado por una fuerza sobre un objeto a medida que el objeto se mueve de un punto a otro es una medida de la medida en que la fuerza contribuye al movimiento. Esto se ilustra en la siguiente imagen en el caso en el que la fuerza dada contribuye al movimiento.
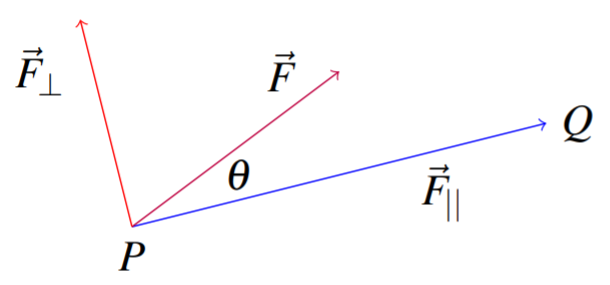
Recordemos que para cualquier vector\(\vec{u}\) en\(\mathbb{R}^n\), podemos escribir\(\vec{u}\) como una suma de dos vectores, como en\[\vec{u} = \vec{u}_{||} + \vec{u}_{\perp}\nonumber \] Para cualquier fuerza\(\vec{F}\), podemos escribir esta fuerza como la suma de un vector en la dirección del movimiento y un vector perpendicular al movimiento. En otras palabras,\[\vec{F} = \vec{F}_{||} + \vec{F}_{\bot}\nonumber \]
En la imagen de arriba la fuerza,\(\vec{F}\) se aplica a un objeto que se mueve en la línea recta de\(P\) a\(Q.\) Hay dos vectores mostrados,\(\vec{F}_{||}\)\(\vec{F}_{\bot }\) y la imagen está destinada a indicar que al agregar estos dos vectores se obtiene\(\vec{F}\). En otras palabras,\(\vec{F} = \vec{F}_{||} + \vec{F}_{\bot}\). Observe que\(\vec{F}_{||}\) actúa en la dirección del movimiento y\(\vec{F}_{\bot }\) actúa perpendicular a la dirección del movimiento. Solo\(\vec{F}_{||}\) contribuye al trabajo realizado por\(\vec{F}\) sobre el objeto a medida que se mueve de\(P\) a\(Q\). \(\vec{F}_{||}\)se llama el componente de la fuerza en la dirección del movimiento. A partir de la trigonometría, se ve la magnitud de\(\vec{F}_{||}\) debe ser igual\( \| \vec{F} \| \left| \cos \theta \right| .\) Así, ya que los\(\vec{F}_{||}\) puntos en la dirección del vector desde\(P\) hasta\(Q,\) el trabajo total realizado deben ser iguales\[ \| \vec{F} \| \| \vec{PQ} \| \cos \theta = \| \vec{F} \| \| \vec{q}-\vec{p} \| \cos \theta\nonumber \]
Ahora, supongamos que el ángulo incluido había sido obtuso. Entonces el trabajo realizado por la fuerza\(\vec{F}\) sobre el objeto habría sido negativo porque\(\vec{F}_{||}\) señalaría en\(-1\) tiempos la dirección del movimiento. En este caso, también\(\cos \theta\) sería negativo y por lo que sigue siendo así que el trabajo realizado estaría dado por la fórmula anterior. Así, a partir de la descripción geométrica del producto punto dada anteriormente, el trabajo es igual a\[ \| \vec{F} \| \| \vec{q}-\vec{p} \| \cos \theta =\vec{F}\bullet \left( \vec{q}-\vec{p}\right)\nonumber \] Esto explica la siguiente definición.
Dejar\(\vec{F}\) ser una fuerza que actúa sobre un objeto que se mueve del punto\(P\) al punto\(Q\), que tienen vectores de posición dados por\(\vec{p}\) y\(\vec{q}\) respectivamente. Entonces el trabajo realizado sobre el objeto por la fuerza dada es igual\(\vec{F}\bullet \left( \vec{q}-\vec{p}\right) .\)
Considera el siguiente ejemplo.
Vamos\(\vec{F}= \left [ \begin{array}{rrr} 2 & 7 & -3 \end{array} \right ]^T\) Newtons. Encuentra el trabajo realizado por esta fuerza en el movimiento del punto\(\left( 1,2,3\right)\) al punto a\(\left( -9,-3,4\right)\) lo largo del segmento de línea recta uniendo estos puntos donde las distancias se miden en metros.
Solución
Primero, compute el vector\(\vec{q} - \vec{p}\), dado por\[\left [ \begin{array}{rrr} -9 & -3 & 4 \end{array} \right ]^T - \left [ \begin{array}{rrr} 1 & 2 & 3 \end{array} \right ]^T = \left [ \begin{array}{rrr} -10 & -5 & 1 \end{array} \right ]^T\nonumber \]
Según Definición\(\PageIndex{3}\) el trabajo realizado es\[\begin{aligned} \left [ \begin{array}{rrr} 2 & 7 & 3 \end{array} \right ]^T \bullet \left [ \begin{array}{rrr} -10 & -5 & 1 \end{array} \right ]^T & =-20+\left( -35\right) +\left( -3\right) \\ & =-58\text{ Newton meters}\end{aligned}\]
Tenga en cuenta que si la fuerza se hubiera dado en libras y la distancia se hubiera dado en pies, las unidades en la obra habrían sido libras pie. En general, el trabajo tiene unidades iguales a unidades de una fuerza por unidades de una longitud. Recordemos que\(1\) Newton metro es igual a\(1\) Joule. Observe también que el trabajo realizado por la fuerza puede ser negativo como en el ejemplo anterior.


