3.3: Intervalos en E
- Page ID
- 113936
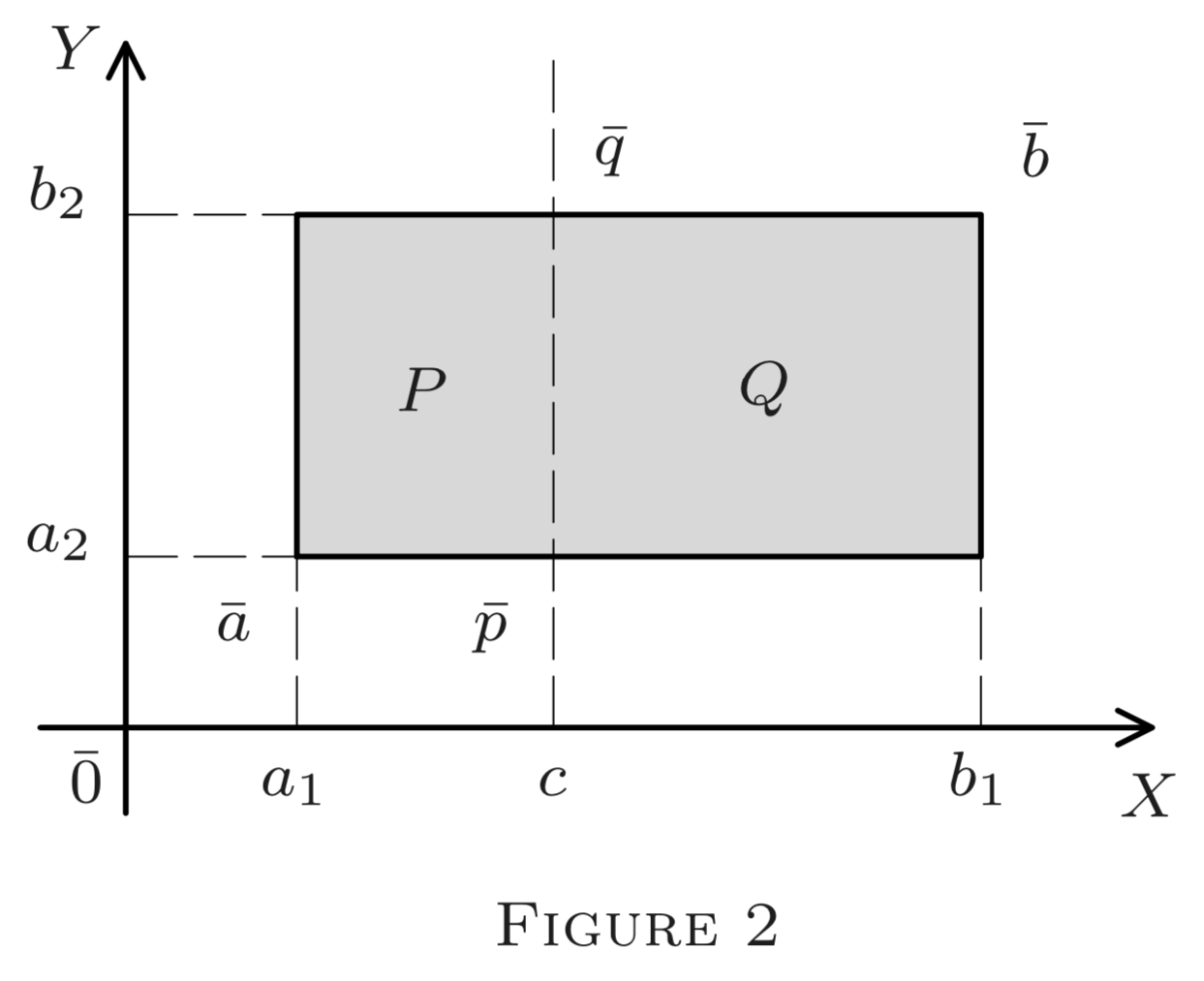
Considera el rectángulo que\(E^{2}\) se muestra en la Figura 2. Su interior (sin el perímetro consta de todos los puntos de\((x, y) \in E^{2}\) tal manera que
\[a_{1}<x<b_{1}\text{ and } a_{2}<y<b_{2};\]
es decir,
\[x \in\left(a_{1}, b_{1}\right)\text{ and } y \in\left(a_{2}, b_{2}\right).\]
Así es el producto cartesiano de dos intervalos de línea,\(\left(a_{1}, b_{1}\right)\) y\(\left(a_{2}, b_{2}\right) .\) Para incluir también todos o algunos lados, tendríamos que reemplazar los intervalos abiertos por los cerrados, semiterrados o medio abiertos. De igual manera, los productos cartesianos de tres intervalos de línea producen paralelepípedos rectangulares en\(E^{3} .\) Llamamos a tales conjuntos en\(E^{n}\) intervalos.
1. Por un intervalo en\(E^{n}\) nos referimos al producto cartesiano de cualquier\(n\) intervalo\(\quad\) en\(E^{1}\) (algunos pueden ser abiertos, algunos cerrados o semiabiertos, etc.).
2. En particular, dado
\[\overline{a}=\left(a_{1}, \ldots, a_{n}\right)\text{ and } \overline{b}=\left(b_{1}, \ldots, b_{n}\right)\]
con
\[a_{k} \leq b_{k}, \quad k=1,2, \ldots, n,\]
definimos el intervalo abierto\((\overline{a}, \overline{b}),\) el intervalo cerrado\([\overline{a}, \overline{b}],\) el intervalo medio abierto\((\overline{a}, \overline{b}],\) y el intervalo semicerrado de la\([\overline{a}, \overline{b})\) siguiente manera:
\[\begin{aligned}(\overline{a}, \overline{b}) &=\left\{\overline{x} | a_{k}<x_{k}<b_{k}, k=1,2, \ldots, n\right\} \\ &=\left(a_{1}, b_{1}\right) \times\left(a_{2}, b_{2}\right) \times \cdots \times\left(a_{n}, b_{n}\right) \\ [\overline{a}, \overline{b}] &=\left\{\overline{x} | a_{k} \leq x_{k} \leq b_{k}, k=1,2, \ldots, n\right\} \\ &=\left[a_{1}, b_{1}\right] \times\left[a_{2}, b_{2}\right] \times \cdots \times\left[a_{n}, b_{n}\right] \\ (\overline{a}, \overline{b}] &=\left\{\overline{x} | a_{k}<x_{k} \leq b_{k}, k=1,2, \ldots, n\right\} \\ &=\left(a_{1}, b_{1}\right] \times\left(a_{2}, b_{2}\right] \times \cdots \times\left(a_{n}, b_{n}\right] \\ [a, b) &=\left\{\overline{x} | a_{k} \leq x_{k}<b_{k}, k=1,2, \ldots, n\right\} \\ &=\left[a_{1}, b_{1}\right) \times\left[a_{2}, b_{2}\right) \times \cdots \times\left[a_{n}, b_{n}\right) \end{aligned}\]
En todos los casos,\(\overline{a}\) y se\(\overline{b}\) denominan los puntos finales del intervalo. Su distancia
\[\rho(\overline{a}, \overline{b})=|\overline{b}-\overline{a}|\]
se llama su diagonal. Las\(n\) diferencias
\[b_{k}-a_{k}=\ell_{k} \quad(k=1, \ldots, n)\]
se llaman sus\(n\) longitudes de borde. Su producto
\[\prod_{k=1}^{n} \ell_{k}=\prod_{k=1}^{n}\left(b_{k}-a_{k}\right)\]
se llama el volumen del intervalo (en\(E^{2}\) ella está su área, en\(E^{1}\) su longitud).\) El punto
\[\overline{c}=\frac{1}{2}(\overline{a}+\overline{b})\]
se llama su centro o punto medio. La diferencia establecida
\[[\overline{a}, \overline{b}]-(\overline{a}, \overline{b})\]
se llama el límite de cualquier intervalo con puntos finales\(\overline{a}\) y\(\vec{b} ;\) consta de 2\(n\) “caras” definidas de manera natural. (¿Cómo?)
A menudo denotamos intervalos por letras simples, por ejemplo. \(A=(\overline{a}, \overline{b}),\)y escribir\(d A\) para “diagonal de\(A^{\prime \prime}\) y\(v A\) o vol\(A\) para “volumen de\(A . "\) Si todas las longitudes de borde\(b_{k}-a_{k}\) son iguales,\(A\) se llama un cubo (en\(E^{2},\) un cuadrado). \(A\)Se dice que el intervalo es degenerado iff\(b_{k}=a_{k}\) para algunos\(k,\) en cuyo caso, claramente,
\[\operatorname{vol} A=\prod_{k=1}^{n}\left(b_{k}-a_{k}\right)=0.\]
Nota 1. Tenemos\(\overline{x} \in(\overline{a}, \overline{b})\) iff las desigualdades se\(a_{k}<x_{k}<b_{k}\) mantienen simultáneamente para todos\(k .\) Esto es imposible si\(a_{k}=b_{k}\) para algunos de\(k ;\) manera similar para las desigualdades\(a_{k}<x_{k} \leq b_{k}\) o\(a_{k} \leq x_{k}<b_{k}\). Así un intervalo degenerado está vacío, a menos que esté cerrado (en cuyo caso contiene\(\overline{a}\) y al\(\overline{b}\) menos).
Nota 2. En cualquier intervalo\(A\),
\[d A=\rho(\overline{a}, \overline{b})=\sqrt{\sum_{k=1}^{n}\left(b_{k}-a_{k}\right)^{2}}=\sqrt{\sum_{k=1}^{n} \ell_{k}^{2}}.\]
En\(E^{2},\) podemos dividir un intervalo\(A\) en dos subintervalos\(P\) y\(Q\) dibujando una línea (ver Figura 2\() .\) En\(E^{3},\) esto se hace por un plano ortogonal a uno de los ejes de la forma\(x_{k}=c\left(\) ver §§4-6, Nota 2\(),\) con\(a_{k}<c<b_{k} .\) En particular, si\ derecho. \(c=\frac{1}{2}\left(a_{k}+b_{k}\right),\)el plano bisecta el borde\(k\) th de\(A ;\) y así la longitud del borde\(k\) th de\(P(\) y es\(Q)\) igual a\(\frac{1}{2} \ell_{k}=\frac{1}{2}\left(b_{k}-a_{k}\right) .\) Si\(A\) está cerrado, así es\(P\) o\(Q,\) dependiendo de nuestra elección. (Podemos incluir la “partición”\(x_{k}=c\) en\(P\) o\(Q . )^{1}\)
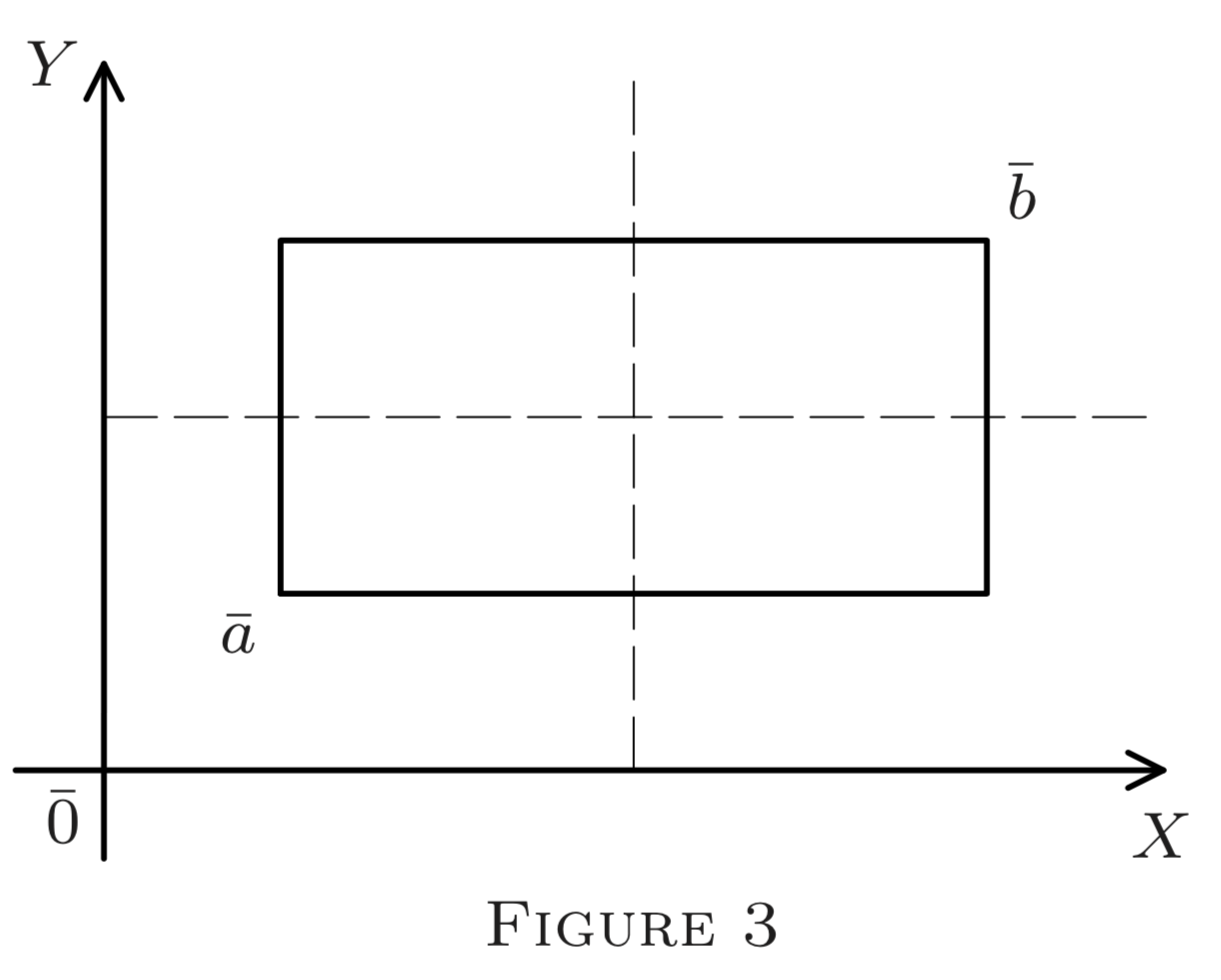
Ahora, sucesivamente dibujar\(n\) planos\(x_{k}=c_{k}, \quad c_{k}=\frac{1}{2}\left(a_{k}+b_{k}\right), \quad k=1,2, \ldots, n .\) El primer plano biseca\(\ell_{j}\) dejando los otros bordes de\(A \mathrm{un}-\) cambiado. Los dos subintervalos resultantes\(P\) y\(Q\) luego son cortados por el plano\(x_{2}=c_{2},\) bisectando el segundo borde en cada uno de ellos. Así obtenemos cuatro subintervalos (ver Figura 3 para\(E^{2}\). Cada plano sucesivo duplica el número de subintervalos. Después de\(n\) los pasos, obtenemos intervalos\(2^{n}\) disjuntos, con todos los bordes\(\ell_{k}\) bisecados. Así por Nota\(2,\) la diagonal de cada uno de ellos es
\[\sqrt{\sum_{k=1}^{n}\left(\frac{1}{2} \ell_{k}\right)^{2}}=\frac{1}{2} \sqrt{\sum_{k=1}^{n} \ell_{k}^{2}}=\frac{1}{2} d A.\]
Nota 3. Si\(A\) se cierra entonces, como se señaló anteriormente, podemos hacer que cualquiera (pero sólo uno\()\) de los\(2^{n}\) subintervalos se cierre manipulando adecuadamente cada paso.
Se deja al lector la prueba de los siguientes corolarios simples.
Ninguna distancia entre dos puntos de un intervalo\(A\) supera\(d A,\) su diagonal. Es decir,\((\forall \overline{x}, \overline{y} \in A) \rho(\overline{x}, \overline{y}) \leq d A\)
Si un intervalo\(A\) contiene\(\overline{p}\) y\(\overline{q},\) luego también\(L[\overline{p}, \overline{q}] \subseteq A\).
Cada intervalo no degenerado en\(E^{n}\) contiene puntos racionales, es decir, puntos cuyas coordenadas son todas racionales.
(Pista: Utilice la densidad de los racionales en\(E^{1}\) para cada coordenada por separado.)