2.8: Optimización
( \newcommand{\kernel}{\mathrm{null}\,}\)
En teoría y aplicaciones, a menudo queremos maximizar o minimizar alguna cantidad. Un ingeniero puede querer maximizar la velocidad de una computadora nueva o minimizar el calor producido por un electrodoméstico. Un fabricante puede querer maximizar las ganancias y la participación de mercado o minimizar el desperdicio. Un estudiante puede querer maximizar una calificación en cálculo o minimizar las horas de estudio necesarias para obtener una calificación en particular.
Sin cálculo, solo sabemos encontrar los puntos óptimos en algunos ejemplos específicos (por ejemplo, sabemos encontrar el vértice de una parábola). Pero, ¿y si necesitamos optimizar una función desconocida?
La mejor manera que tenemos sin cálculo es examinar la gráfica de la función, quizás usando tecnología. Pero nuestra vista depende de la ventana de visualización que elegimos; podríamos perder algo importante. Además, probablemente solo obtendremos una aproximación de esta manera. (En algunos casos, eso será lo suficientemente bueno.)
El cálculo proporciona formas de reducir drásticamente el número de puntos que necesitamos examinar para encontrar las ubicaciones exactas de máximos y mínimos, mientras que al mismo tiempo nos asegura que no nos hemos perdido nada importante.
Locales Maxima y Minima
Antes de examinar cómo el cálculo puede ayudarnos a encontrar máximos y mínimos, necesitamos definir los conceptos que desarrollaremos y usaremos.
f(x)tiene un máximo local enx=a sif(a) \geq f(x) para todosx cercaa.
f(x)tiene un mínimo local enx=a sif(a) \leq f(x) para todosx cercaa.
f(x)tiene un extremo local enx=a sif(a) es un máximo o mínimo local.
Los plurales de estos son máximos y mínimos. A menudo simplemente decimos “max” o “min”; ahorra muchas sílabas.
Algunos libros dicen “relativo” en lugar de “local”.
El proceso de búsqueda de máximos o mínimos se llama optimización.
Un punto es un máximo local (o min) si es mayor (menor) que todos los puntos cercanos. Estos puntos provienen de la forma de la gráfica.
f(x)tiene un máximo global enx=a sif(a) \geq f(x) por todosx en el dominio def(x).
f(x)tiene un mínimo global enx=a sif(a) \leq f(x) para todosx en el dominio def(x).
f(x)tiene un extremo global enx=a sif(a) es un máximo o mínimo global.
Algunos libros dicen “absoluto” en lugar de “global”.
Un punto es un máximo (o mínimo) global si es mayor (menor) que cada punto de la gráfica. Estos puntos provienen de la forma de la gráfica y de la ventana a través de la cual vemos la gráfica.
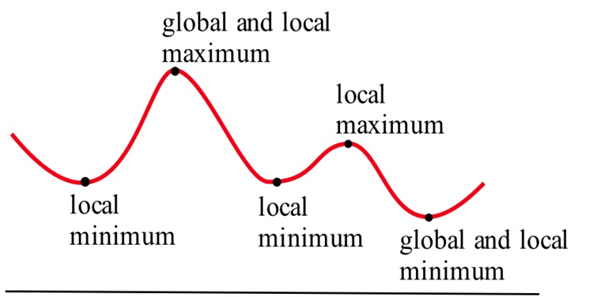
Se etiquetan los extremos locales y globales de la función en la Figura 1. Deberías notar que cada extremo global también es un extremo local, pero hay extremos locales que no son extremos globales.
Sih(x) es la altura de la tierra sobre el nivel del mar en la ubicaciónx, entonces el máximo global deh esh (cumbre del monte. Everest) = 29,028 pies. El máximo local deh para Estados Unidos esh (cumbre del monte. McKinley) = 20,320 pies. El mínimo local deh para Estados Unidos esh (Valle de la Muerte) = -282 pies.
La tabla muestra las inscripciones anuales de cálculo en una universidad grande. ¿Qué años tuvieron inscripciones locales de cálculo máximo o mínimo? ¿Cuáles fueron las inscripciones máximas y mínimas globales en cálculo?
| Año | 2000 | 2001 | 2002 | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 |
| Matrícula | 1257 | 1324 | 1378 | 1336 | 1389 | 1450 | 1523 | 1582 | 1567 | 1545 | 1571 |
Hubo máximos locales en 2002 y 2007; el máximo global fue de 1582 estudiantes en 2007. Hubo mínimos locales en 2003 y 2009; el mínimo global fue de 1257 estudiantes en 2000. Elegimos no pensar en 2000 como mínimo local o 2010 como máximo local; sin embargo, algunos libros incluirían los puntos finales. Se nos permite tener un máximo global o mínimo global en un punto final.
Encontrar máximos y mínimos de una función
¿Cómo debe ser la línea tangente en un máximo o mínimo local? Mira estas dos gráficas otra vez — verás que en todos los puntos extremos, la línea tangente es horizontal (entoncesf' = 0). Hay una cúspide en la gráfica azul — la línea tangente es vertical allí (entonces nof' está definida).
Eso nos da la pista de cómo encontrar valores extremos.
Un número crítico para una funciónf is a value x = a in the domain of f where either f'(a) = 0 or f'(a) is undefined.
Un punto crítico para una funciónf is a point (a, f(a)) where a is a critical number of f.
Un máximo o mínimo local de solof puede ocurrir en un punto crítico.
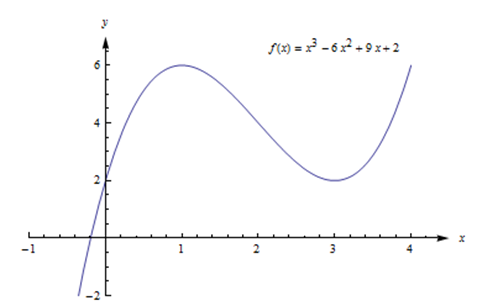
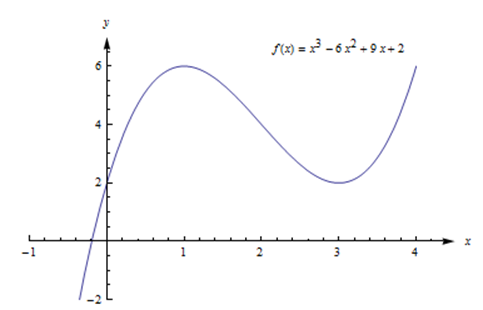
Encuentra los puntos críticos def(x) = x^3 - 6x^2 + 9x + 2.
Un número crítico def puede ocurrir solo dondef'(x) = 0 o dondef' no existe.
f '(x) = 3x^2 - 12x + 9 = 3(x^2 - 4x + 3) = 3(x - 1)(x - 3)\nonumber Entoncesf'(x) = 0 atx = 1 yx = 3 (y ningún otro valor de x ). No hay lugares dondef' esté indefinido.
Los números críticos sonx = 1 yx= 3. Entonces los puntos críticos son (1, 6) y (3, 2).
Estas son las únicas ubicaciones posibles de los extremos locales def. Todavía no hemos discutido cómo saber si alguno de estos puntos es en realidad un extremo local def, o de qué tipo podría ser. Pero podemos estar seguros de que ningún otro punto es un extremo local.
La gráfica def abajo muestra que(1, f(1) ) = (1, 6) es un máximo local y(3, f(3) ) = (3, 2) es un mínimo local. Esta función no tiene un máximo o mínimo global.
Encuentra todos los extremos locales def(x) = x^3.
f(x) = x^3es diferenciable para todosx, yf'(x) = 3x^2. El único lugar dondef'(x) = 0 se encuentrax = 0, por lo que el único candidato es el punto crítico (0,0).
Six \gt 0 entoncesf(x) = x^3 \gt 0 = f(0), entonces nof(0) es un máximo local.
De igual manera, six \lt 0 entoncesf(x) = x^3 \lt 0 = f(0) así nof(0) es un mínimo local.
El punto crítico (0,0) es el único candidato para ser un extremo local def, y, con base en la gráfica, este candidato no resultó ser un extremo local def. La funciónf(x) = x^3 no tiene extremos locales.
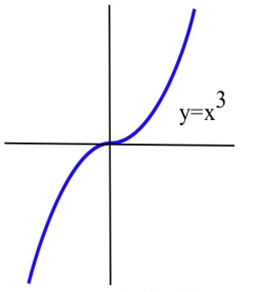
¡Recuerda este ejemplo! No basta con encontrar los puntos críticos —sólo podemos decir quef podría tener un extremo local en los puntos críticos.
Pruebas de Primera y Segunda Derivada
¿Ese punto crítico es un Máximo o Mínimo (o Ninguno)?
Una vez que hemos encontrado los puntos críticos def, todavía tenemos el problema de determinar si estos puntos son máximos, mínimos o ninguno.
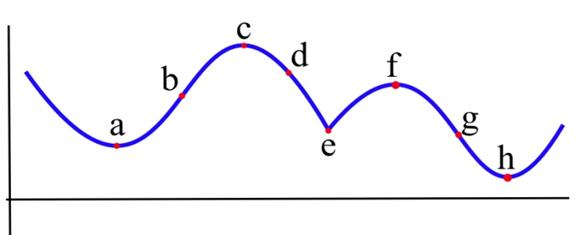
Todas las gráficas de la siguiente figura tienen un punto crítico en (2, 3). De las gráficas se desprende que el punto (2,3) es un máximo local en (a) y (d), (2,3) es un mínimo local en (b) y (e), y (2,3) no es un extremo local en (c) y (f).
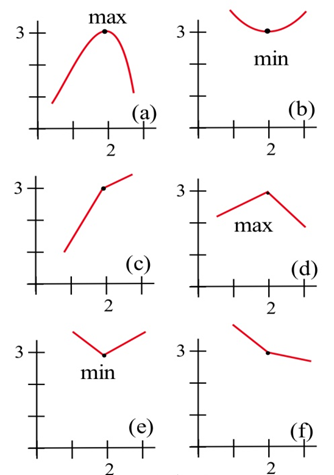
Los números críticos solo dan las posibles ubicaciones de los extremos, y algunos números críticos no son las ubicaciones de los extremos. Los números críticos son los candidatos para las ubicaciones de máximos y mínimos.
f'y Valores Extremos def
Aquí se muestran cuatro formas posibles de gráficas — en cada gráfica, el punto marcado por una flecha es un punto crítico, dondef'(x) = 0. ¿Qué sucede con la derivada cerca del punto crítico?

A un máximo local, como en la gráfica de la izquierda, la función aumenta a la izquierda del máximo local, luego disminuye a la derecha. La derivada es primero positiva, luego negativa a un máximo local. A un min local, la función disminuye hacia la izquierda y aumenta hacia la derecha, por lo que la derivada es primero negativa, luego positiva. Cuando no hay un extremo local, la función continúa aumentando (o disminuyendo) justo más allá del punto crítico, la derivada no cambia de signo.
Encuentra los puntos críticos def.
Para cada número críticoc, examinar el signo def’ a la izquierda y a la derecha dec. ¿Qué pasa con el letrero a medida que te mueves de izquierda a derecha?
- Sif'(x) cambia de positivo a negativo enx = c, entoncesf tiene un máximo local en(c, f(c)).
- Sif'(x) cambia de negativo a positivo enx = c, entoncesf tiene un mínimo local en(c, f(c)).
- Sif'(x) no cambia signo enx = c, entonces no(c, f(c)) es ni un máximo local ni un mínimo local.
Encuentre los puntos críticos def(x) = x^3 - 6x^2 + 9x + 2 y clasifíquelos como máximo local, mínimo local o ninguno.
Ya encontramos los puntos críticos; son (1, 6) y (3, 2).
Ahora podemos usar la primera prueba derivada para clasificar cada una. Recordemos esof'(x) = 3x^2 - 12x + 9 = 3(x^2 - 4x + 3) = 3(x - 1)(x - 3). La forma factorizada es más fácil de trabajar aquí, así que usemos eso.
En (1, 6) podríamos elegir un número ligeramente menor que 1 para conectarlo a la fórmula paraf' — tal vez usarx = 0, ox = 0.9. Entonces podríamos examinar su signo. Pero no nos importa el valor numérico, lo único que nos interesa es su signo. Y para eso, no tenemos que hacer ningún enchufar:
- Six es un poco menor que 1, entoncesx-1 es negativo, yx-3 es negativo. Asíf' = 3(x - 1)(x - 3) será pos (neg) (neg) = positivo.
- Porx un poco más de 1, podemos evaluarf' en un número más de 1 (pero menos de 3, ¡no queremos pasar el siguiente punto crítico!) — tal vezx = 2. O podemos hacer un argumento de signo rápido como lo que hicimos anteriormente: parax un poco más de 1,f' = 3(x - 1)(x - 3) será pos (pos) (neg) = negativo.
Entoncesf' cambia de positivo a negativo, lo que significa que hay un máximo local en (1, 6).
Como otro enfoque, podríamos trazar una recta numérica, y marcar los números críticos:
Ya sabemos que la derivada es cero o indefinida en los números críticos. En cada intervalo entre estos valores, la derivada permanecerá en el mismo signo. Para determinar el signo, podríamos elegir un valor de prueba en cada intervalo, y evaluar la derivada en esos puntos (o usar el enfoque de signo utilizado anteriormente).
A (3, 2)f' cambia de negativo a positivo, por lo que hay un min local a (3, 2). Esto confirma lo que vimos antes en la gráfica.
f''y Valores Extremos def
La concavidad de una función también puede ayudarnos a determinar si un punto crítico es un máximo o mínimo o ninguno. Por ejemplo, si un punto está en la parte inferior de una función cóncava hacia arriba, entonces el punto es mínimo.
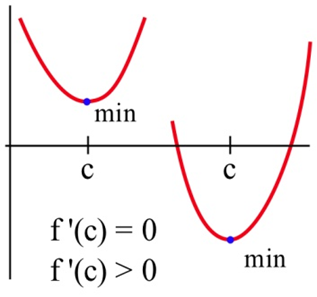
Encuentra todos los puntos críticos def. For those critical points where f'(c) = 0, find f''(c).
- Sif''(c) \lt 0 (negativo) entoncesf es cóncavo hacia abajo y tiene un máximo local enx = c.
- Sif''(c) \gt 0 (positivo) entoncesf es cóncavo hacia arriba y tiene un mínimo local enx = c.
- Sif''(c) = 0 entoncesf puede tener un máximo local, un mínimo o ninguno alx = c.
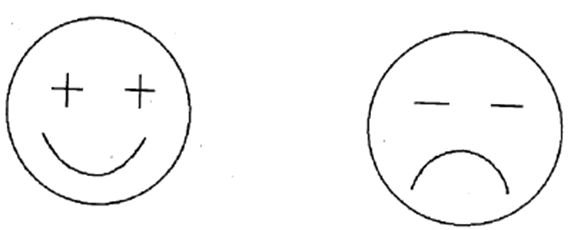
Las caras de dibujos animados pueden ayudarte a recordar la Segunda Prueba Derivada.
f(x) = 2x^3 - 15x^2 + 24x - 7tiene los números críticosx = 1 y 4. Utilice la Prueba de Segunda Derivada para Extremos para determinar sif(1) yf(4) son máximos o mínimos o ninguno.
Tenemos que encontrar la segunda derivada: \begin{align*} f(x) & = 2x^3 - 15x^2 + 24x - 7\\ f'(x) & = 6x^2 - 30x + 24\\ f''(x) & = 12x - 30 \end{align*} \nonumber
Entonces solo necesitamos evaluarf'' en cada número crítico:
x = 1: f''(1)=12(1)-30 \lt 0 , por lo que hay un máximo local enx = 1.
x = 4: f''(4)=12(4)-30 \gt 0 , por lo que hay un mínimo local enx = 4.
A muchos estudiantes les gusta la Segunda Prueba Derivada. La Prueba de Segunda Derivada suele ser más fácil de usar que la Prueba de Primera Derivada. Sólo hay que encontrar el signo de un número por cada número crítico en lugar de dos. Y si tu función es un polinomio, su segunda derivada probablemente será una función más simple que la derivada.
Sin embargo, si necesitabas una regla de producto, regla de cociente o regla de cadena para encontrar la primera derivada, encontrar la segunda derivada puede ser mucho trabajo. Además, aunque la segunda derivada sea fácil, la Prueba de Segunda Derivada no siempre da respuesta. La Primera Prueba Derivada siempre te dará una respuesta.
Usa la prueba que quieras. Pero recuerde, tiene que hacer alguna prueba para asegurarse de que su punto crítico en realidad es un máximo o mínimo local.
Máximas y Mínimas Globales
En las aplicaciones, muchas veces queremos encontrar el extremo global; saber que un punto crítico es un extremo local no es suficiente.
Por ejemplo, si queremos obtener el mayor beneficio, queremos obtener el beneficio absolutamente mayor de todos. ¿Cómo encontramos global max y min?
Solo hay algunas cosas adicionales en las que pensar.
Extremos de punto final
Los extremos locales de una función ocurren en puntos críticos, estos son puntos en la función que podemos encontrar pensando en la forma (y usando la derivada para ayudarnos). Pero si estamos viendo una función en un intervalo cerrado, los puntos finales podrían ser extremos. Estos extremos de punto final no están relacionados con la forma de la función; tienen que ver con el intervalo, la ventana a través de la cual estamos viendo la función.
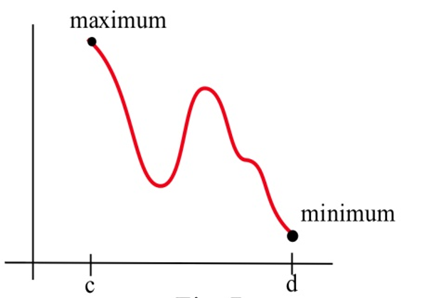
En la gráfica anterior, aparece que hay tres puntos críticos —un mínimo local, un máximo local y uno que no es ninguno de los dos. Pero el máximo global, el punto más alto de todos, está en el punto final izquierdo. El mínimo global, el punto más bajo de todos, está en el punto final correcto.
¿Cómo decidimos si los endpoints son globales max o min? Es más fácil de lo que esperaba: simplemente conecte los puntos finales, junto con todos los números críticos, y comparey los valores.
Esta técnica se puede utilizar cuando se trata de encontrar extremos globales en un intervalo limitado.
Los únicos lugares donde una función puede tener un extremo global en un intervalo limitado son en puntos críticos o puntos finales.
- Si la función solo tiene un punto crítico, y es un extremo local, entonces también es el extremo global.
- Si hay puntos finales, encuentre los extremos globales comparandoy -valores en todos los puntos críticos y en los puntos finales.
- En caso de duda, grafica la función para estar seguro. (Sin embargo, a menos que el problema te indique explícitamente lo contrario, no basta con usar la gráfica para obtener tu respuesta).
Encuentra el máximo y el mínimo global def(x) = x^3 - 3x^2 - 9x + 5 for-2 \leq x \leq 6.
f'(x) = 3x^2 - 6x - 9 = 3(x + 1)(x - 3). Necesitamos encontrar puntos críticos, y tenemos que verificar los puntos finales.
f'(x) = 3(x + 1)(x - 3) = 0cuándox = -1 yx = 3. Los puntos finales del intervalo sonx = -2 yx = 6.
Ahora simplemente comparamos los valores def a estos cuatro valores dex:
| x | f(x) |
| -2 | 3 |
| -1 | 10 |
| 3 | -22 |
| 6 | 59 |
El mínimo global def on[ -2, 6] es -22, cuandox = 3, y el máximo global def on[ -2, 6] es 59, cuandox = 6.
¡Ten cuidado! Sólo se puede utilizar esta técnica (evaluando la función en puntos finales y valores críticos) para determinar los extremos globales en un intervalo limitado.
Si alguna pregunta pregunta por extremos locales, debes usar la primera o segunda prueba derivada descrita anteriormente en la sección.
Si solo hay un punto crítico
Si la función tiene solo un punto crítico y es un máximo local (o min), entonces debe ser el máximo global (o min). Para ver esto, piensa en la geometría. Mira la gráfica de la izquierda — hay un máximo local, y la gráfica baja a ambos lados del punto crítico. Supongamos que hubiera algún otro punto que fuera más alto —entonces la gráfica tendría que dar la vuelta. Pero ese punto de inflexión se habría mostrado como otro punto crítico. Si solo hay un punto crítico, entonces la gráfica nunca podrá dar la vuelta atrás.
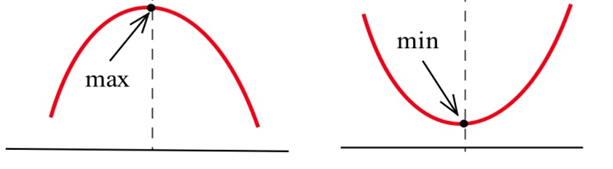
En caso de duda, gráficalo y mira.
Si estás tratando de encontrar un máximo o mínimo global en un intervalo abierto (o toda la línea real), y hay más de un punto crítico, entonces necesitas mirar la gráfica para decidir si hay un máximo global o un mínimo. Asegúrate de que todos tus puntos críticos se muestren en tu gráfica, y que graficas más allá de ellos, eso te dirá lo que quieres saber.
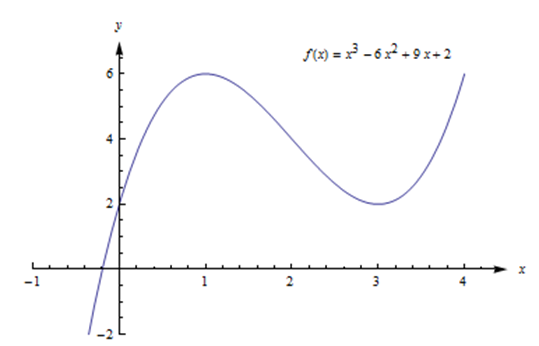
Encuentra el máximo global y el mínimo def(x) = x^3 - 6x^2 + 9x + 2.
Anteriormente hemos encontrado que (1, 6) es un máximo local y (3, 2) es un min local. Esto no es un intervalo cerrado, y hay dos puntos críticos, por lo que debemos recurrir a la gráfica de la función para encontrar el máximo global y el mínimo.
La gráfica def muestra que los puntos a la izquierda dex = 4 tieneny -valores mayores a 6, por lo que (1, 6) no es un máximo global. Asimismo, six es negativo,y es menor que 2, por lo que (3, 2) no es un mínimo global. No hay puntos finales, así que hemos agotado todas las posibilidades. Esta función no tiene un máximo o mínimo global.