10.3: Función Gamma

Última actualización
Guardar como PDF

Page ID: 113669

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Para$\nu$ no un entero la relación de recursión para la función de Bessel genera algo muy similar a los factoriales. Estas cantidades se expresan más fácilmente en algo llamado función gamma, definida como

\[\Gamma(\nu) = \int_0^\infty e^{-t}t^{\nu-1} dt,\;\;\;\nu>0. \nonumber \]

Algunas propiedades especiales de la$\Gamma$ función ahora siguen inmediatamente:

\[\begin{aligned} \Gamma(1) & = & \int_0^\infty e^{-t}dt = \left.-e^{-1}\right|^\infty_0 =1-e^{-\infty}=1\nonumber\\ \Gamma(\nu) & = & \int_0^\infty e^{-t} t^{\nu-1} dt = -\int_0^\infty \frac{de^{-t}}{dt} t^{\nu-1} dt\nonumber\\ &=& \left.- e^{-t} t^{\nu-1} \right|^\infty_0 +(\nu-1) \int_0^\infty e^{-t} t^{\nu-2} dt \end{aligned} \nonumber \]

El primer término es cero, y obtenemos\[\Gamma(\nu) = (\nu-1)\Gamma(\nu-1) \nonumber \]

De esto concluimos que

\[\Gamma(2)=1\cdot1=1,\;\Gamma(3)=2\cdot1\cdot1=2,\; \Gamma(4)=3\cdot2\cdot1\cdot1=2,\;\Gamma(n) = (n-1)!. \nonumber \]

Así para el argumento entero la$\Gamma$ función no es más que un factorial, sino que también se define para otros argumentos. Este es el sentido en el que$\Gamma$ generaliza los argumentos factoriales a no enteros. Uno debe darse cuenta de que una vez que se conoce la$\Gamma$ función entre los valores de su argumento de, digamos, 1 y 2, se puede evaluar cualquier valor de la$\Gamma$ función a través de la recursión. Teniendo en cuenta que$\Gamma(1.65) = 0.9001168163$ encontramos

\[\Gamma(3.65) = 2.65\times1.65\times0.9001168163 = 3.935760779 . \nonumber \]

Ejercicio$\PageIndex{1}$

Evaluar$\Gamma(3)$,$\Gamma(11)$,$\Gamma(2.65)$.

Contestar: $2!=2$,$10!=3628800$,$1.65\times0.9001168163=1.485192746$.

También nos gustaría determinar la$\Gamma$ función para$\nu<1$. Se puede invertir la relación de recursividad para leer\[\Gamma(\nu-1) = \frac{\Gamma(\nu)}{\nu-1}, \nonumber \]$\Gamma(0.7) = \Gamma(1.7)/0.7=0.909/0.7=1.30$.

¿$\Gamma(\nu)$Para qué sirve$\nu<0$? Vamos a repetir la recursión derivada anteriormente y encontrar\[\Gamma(-1.3) = \frac{\Gamma(-0.3)}{-1.3} = \frac{\Gamma(0.7)}{-1.3\times -0.3} = \frac{\Gamma(1.7)}{0.7\times-0.3\times -1.3}=3.33\;. \nonumber \] Esto funciona para cualquier valor del argumento que no sea un entero. Si el argumento es entero nos metemos en problemas. Mira$\Gamma(0)$. Para pequeños positivos$\epsilon$\[\Gamma(\pm\epsilon)= \frac{\Gamma(1\pm\epsilon)}{\pm\epsilon} =\pm \frac{1}{\epsilon}\rightarrow \pm \infty. \nonumber \] Así no$\Gamma(n)$ se define para$n\leq0$. Esto se puede ver fácilmente en la gráfica de la$\Gamma$ función, Fig. $\PageIndex{1}$.

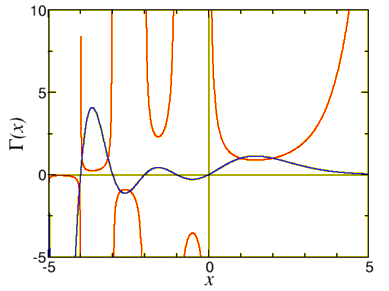
$f12.png$

Figura$\PageIndex{1}$: Gráfica de la$\Gamma$ función (línea continua). También$1/\Gamma$ se incluye la inversa (línea discontinua). Tenga en cuenta que esta última función no es discontinua.

Por último, en problemas físicos uno utiliza a menudo$\Gamma(1/2)$,\[\Gamma(\frac{1}{2}) = \int_0^\infty e^{-t}t^{-1/2} dt = 2\int_0^\infty e^{-t}dt^{1/2} = 2\int_0^\infty e^{-x^2}dx. \nonumber \] Esto puede ser evaluado por un truco muy inteligente, primero evaluamos$\Gamma(1/2)^2$ usando coordenadas polares\[\begin{aligned} \Gamma(\frac{1}{2})^2 &=& 4 \int_0^\infty e^{-x^2}dx\int_0^\infty e^{-y^2}dy \nonumber\\ &=& 4 \int_0^\infty \int_0^{\pi/2} e^{-\rho^2}\rho d\rho d\phi = \pi.\end{aligned} \nonumber \] (Ver la discusión de coordenadas polares en la Sec. 7.1.) Así encontramos\[\Gamma(1/2)=\sqrt{\pi},\;\;\Gamma(3/2)=\frac{1}{2}\sqrt{\pi},\;\;{\rm etc.} \nonumber \]