11.1: Modelado del ojo

Déjame modelar la temperatura en un modelo sencillo del ojo, donde el ojo es una esfera, y los párpados son circulares. En ese caso podemos poner el\(z\) eje -recto por la mitad del ojo, y podemos suponer que la temperatura sólo depende de\(r,\theta\) y no de\(\phi\). Suponemos que la parte del ojo en contacto con el aire está a una temperatura de\(20^{\circ}\) C, y la parte en contacto con el cuerpo está en\(36^{\circ}\) C.

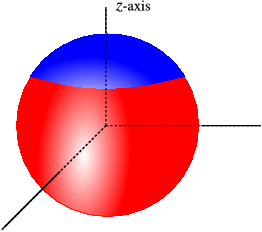
Figura\(\PageIndex{1}\): La temperatura en el exterior de un modelo simple del ojo

Si buscamos la temperatura de estado estacionario se describe por la ecuación de Laplace,

\[{ \nabla}^{2} u(r,\theta) =0. \nonumber \]

Expresando el laplaciano\({ \nabla}^{2}\) en coordenadas esféricas (ver capítulo 7) encontramos

\[\frac{1}{r^{2}}\dfrac{\partial}{\partial r}{~}\left(r^{2}\dfrac{\partial}{\partial r} u \right) +\frac{1}{r^{2}\sin\theta} \dfrac{\partial}{\partial \theta}{~}\left(\sin\theta\dfrac{\partial}{\partial \theta} u\right) =0. \nonumber \]

Una vez más resolvemos la ecuación por separación de variables,

\[u(r,\theta) = R(r) T (\theta). \nonumber \]

Después de esta sustitución nos damos cuenta de que

\[\frac{[r^{2} R']'}{R} = -\frac{[\sin\theta T']'}{T\sin\theta} = \lambda. \nonumber \]

Se\(R\) mostrará que la ecuación para es fácil de resolver (más adelante). El para\(T\) es de mucho más interés. Ya que para los problemas 3D la dependencia angular es más complicada, mientras que en 2D las funciones angulares eran solo senos y cosenos.

La ecuación para\(T\) es

\[[\sin\theta T']'+\lambda T\sin\theta=0. \nonumber \]

Esta ecuación se llama ecuación de Legendre, o en realidad lleva ese nombre después de cambiar las variables a\(x= \cos\theta\). Desde\(\theta\) corre de\(0\) a\(\pi\), nos encontramos\(\sin \theta >0\), y tenemos

\[\sin\theta = \sqrt{1-x^{2}}. \nonumber \]

Después de esta sustitución estamos haciendo el cambio de variables encontramos la ecuación (\(y(x)=T(\theta)=T(\arccos x)\), y ahora diferenciamos w.r.t.\(x\),\(d/d\theta = - \sqrt{1-x^{2}}d/dx\))

\[\frac{d}{dx}\left[(1-x^{2})\frac{dy}{dx}\right] + \lambda y = 0. \nonumber \]

Esta ecuación se ve fácilmente como autoadconjunta. No es muy difícil demostrar que\(x=0\) es un punto regular (no singular) — pero la ecuación es singular en\(x=\pm 1\). Cerca\(x=0\) podemos resolverlo mediante la sustitución directa de una serie Taylor,

\[y(x) = \sum_{j=0} a_{j} x^{j}. \nonumber \]

Encontramos la ecuación

\[\sum_{j=0}^{\infty}j(j-1) a_{j} x^{j-2} -\sum_{j=0}^{\infty}j(j-1) a_{j} x^{j} -2\sum_{j=0}^{\infty}j a_{j} x^{j} + \lambda \sum_{j=0}^{\infty} a_{j} x^{j} = 0 \nonumber \]

Después de introducir la nueva variable\(i=j-2\), tenemos

\[\sum_{j=0}^{\infty}(i+1)(i+1) a_{i+2} x^{i} -\sum_{j=0}^{\infty}[j(j+1)-\lambda] a_{j} x^{j}=0. \nonumber \]

Recogiendo los términos del pedido\(x^{k}\), encontramos la relación de recurrencia\[a_{k+2} = \frac{k(k+1)-\lambda}{(k+1)(k+2)} a_{k}. \nonumber \]

Si\(\lambda=n(n+1)\) esta serie termina —en realidad esas son las únicas soluciones aceptables, cualquiera que\(\lambda\) tome un valor diferente realmente diverge en\(x=+1\) o\(x=-1\), no es aceptable para una cantidad física— no puede simplemente divergir en el polo norte o sur (\(x=\cos\theta=\pm 1\)son el norte y polo sur de una esfera).

Por lo tanto, tenemos,\(n\) incluso,

\[y_{n} = a_{0}+a_{2}x^{2}+\ldots+a_{n}x^{n}. \nonumber \]

Para impar\(n\) encontramos polinomios impares,

\[y_{n} = a_{1}x+a_{3}x^{3}+\ldots+a_{n}x^{n}. \nonumber \]

Uno define convencionalmente\[a_{n} = \frac{(2n)!}{n!^{2} 2^{n}}. \nonumber \]

Con esta definición obtenemos

\[\begin{array}{lllllll} P_{0}& =& 1, &~~~&P_{1} & =& x,\\ P_{2}&=& \frac{3}{2}x^{2}-\frac{1}{2},&&P_{3}&=&\dfrac{1}{2}(5x^3-3x),\\ P_4 &=& \frac{1}{8}(35x^{4}-30x^{2}+3) ,&& P_5 &=& \frac{1}{8}(63x^{5}-70x^{3}+15x) . \end{array} \nonumber \]

Una gráfica de estos polinomios se puede encontrar en la figura\(\PageIndex{2}\).

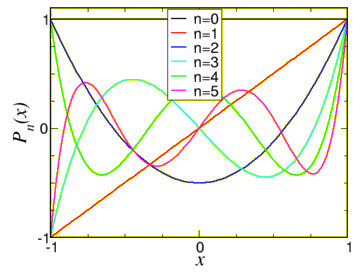
Figura\(\PageIndex{2}\): Los primeros polinomios de Legendre\(P_n(x)\).