2.2: El límite de una función

Última actualización
Guardar como PDF

Page ID: 116842

Edwin “Jed” Herman & Gilbert Strang
OpenStax

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)

Objetivos de aprendizaje

Usando la notación correcta, describa el límite de una función.
Utilice una tabla de valores para estimar el límite de una función o para identificar cuándo no existe el límite.
Utilice una gráfica para estimar el límite de una función o para identificar cuándo no existe el límite.
Defina límites unilaterales y proporcione ejemplos.
Explicar la relación entre los límites unilaterales y biolaterales.
Usando la notación correcta, describa un límite infinito.
Definir una asíntota vertical.

El concepto de un proceso límite o limitante, esencial para la comprensión del cálculo, existe desde hace miles de años. De hecho, los matemáticos primitivos utilizaron un proceso limitante para obtener mejores y mejores aproximaciones de áreas de círculos. Sin embargo, la definición formal de un límite —tal como lo conocemos y entendemos hoy— no apareció hasta finales del siglo XIX. Por lo tanto, comenzamos nuestra búsqueda para comprender los límites, como lo hicieron nuestros antepasados matemáticos, utilizando un enfoque intuitivo. Al final de este capítulo, armado con una comprensión conceptual de los límites, examinamos la definición formal de un límite.

Comenzamos nuestra exploración de límites echando un vistazo a las gráficas de las funciones

\(f(x)=\dfrac{x^2−4}{x−2}\),
\(g(x)=\dfrac{|x−2|}{x−2}\), y
\(h(x)=\dfrac{1}{(x−2)^2}\),

que se muestran en la Figura\(\PageIndex{1}\). En particular, enfoquemos nuestra atención en el comportamiento de cada gráfica en y alrededor\(x=2\).

Tres gráficas de funciones. El primero es f (s) = (x^2 — 4)/(x-2), que es una línea de pendiente, x intercepción (-2,0), y círculo abierto en (2,4). El segundo es g (x) = |x — 2 |/(x-2), que contiene dos líneas: x=1 para x — Figura\(\PageIndex{1}\): Estas gráficas muestran el comportamiento de tres funciones diferentes alrededor\(x=2\).

Cada una de las tres funciones está indefinida en\(x=2\), pero si hacemos esta afirmación y ninguna otra, damos una imagen muy incompleta de cómo se comporta cada función en las proximidades de\(x=2\). Para expresar el comportamiento de cada gráfica en las proximidades de una manera\(2\) más completa, necesitamos introducir el concepto de límite.

Definición intuitiva de un límite

Primero echemos un vistazo más de cerca a cómo se\(f(x)=(x^2−4)/(x−2)\) comporta la función alrededor de\(x=2\) la Figura\(\PageIndex{1}\). Como los valores de\(x\) aproximación\(2\) de ambos lados de\(2\), los valores de\(y=f(x)\) aproximación\(4\). Matemáticamente, decimos que el límite de\(f(x)\) como\(2\) se\(x\) acerca es\(4\). Simbólicamente, expresamos este límite como

\(\displaystyle \lim_{x \to 2} f(x)=4\).

A partir de esta breve mirada informal a un límite, comencemos a desarrollar una definición intuitiva del límite. Podemos pensar en el límite de una función en un número\(a\) como el único número real al\(L\) que se acercan los valores funcionales como el enfoque\(x\) -valores\(a\), siempre que\(L\) exista tal número real. Dicho con más cuidado, tenemos la siguiente definición:

Definición (Intuitivo): Límite

Dejar\(f(x)\) ser una función definida en todos los valores en un intervalo abierto conteniendo\(a\), con la posible excepción de\(a\) sí misma, y dejar\(L\) ser un número real. Si todos los valores de la función se\(f(x)\) acercan al número real\(L\) como los valores de\(x(≠a)\) acercarse al número\(a\), entonces decimos que el límite de\(f(x)\) como\(a\) se\(x\) acerca es\(L\). (Más sucinto, a medida que\(x\) se acerca\(a\),\(f(x)\) se acerca y se queda cerca de\(L\).) Simbólicamente, expresamos esta idea como

\[\lim_{x \to a} f(x)=L. \label{limit} \]

Podemos estimar límites construyendo tablas de valores funcionales y observando sus gráficas. Este proceso se describe en la siguiente Estrategia de Resolución de Problemas.

Estrategia de resolución de problemas: evaluación de un límite usando una tabla de valores funcionales

1. Para evaluar\(\displaystyle \lim_{x \to a} f(x)\), comenzamos por completar una tabla de valores funcionales. Deberíamos elegir dos conjuntos de\(x\) valores: un conjunto de valores aproximados\(a\) y menores que\(a\), y otro conjunto de valores que se aproximan\(a\) y mayores que\(a\). La tabla\(\PageIndex{1}\) demuestra cómo se verían tus mesas.

Mesa\(\PageIndex{1}\)
\(x\)	\(f(x)\)	\(x\)	\(f(x)\)
\ (x\)” style="text-align:center; ">\(a-0.1\)	\ (f (x)\)” style="text-align:center; ">\(f(a-0.1)\)	\ (x\)” style="text-align:center; ">\(a+0.1\)	\ (f (x)\)” style="text-align:center; ">\(f(a+0.1)\)
\ (x\)” style="text-align:center; ">\(a-0.01\)	\ (f (x)\)” style="text-align:center; ">\(f(a-0.01)\)	\ (x\)” style="text-align:center; ">\(a+0.01\)	\ (f (x)\)” style="text-align:center; ">\(f(a+0.01)\)
\ (x\)” style="text-align:center; ">\(a-0.001\)	\ (f (x)\)” style="text-align:center; ">\(f(a-0.001)\)	\ (x\)” style="text-align:center; ">\(a+0.001\)	\ (f (x)\)” style="text-align:center; ">\(f(a+0.001)\)
\ (x\)” style="text-align:center; ">\(a-0.0001\)	\ (f (x)\)” style="text-align:center; ">\(f(a-0.0001)\)	\ (x\)” style="text-align:center; ">\(a+0.0001\)	\ (f (x)\)” style="text-align:center; ">\(f(a+0.0001)\)
\ (f (x)\)” rowspan="1" style="text-align:center; ">Utilice valores adicionales según sea necesario.		\ (f (x)\)” rowspan="1" style="text-align:center; ">Utilice valores adicionales según sea necesario.

2. A continuación, veamos los valores en cada una de las\(f(x)\) columnas y determinemos si los valores parecen acercarse a un solo valor a medida que bajamos cada columna. En nuestras columnas, observamos la secuencia\(f(a−0.1)\),\(f(a−0.01)\)\(f(a−0.001)\),\(f(a−0.0001)\),, y así sucesivamente\(f(a+0.1), \;f(a+0.01), \;f(a+0.001), \;f(a+0.0001)\), y así sucesivamente. (Nota: Aunque hemos elegido los\(x\) -valores\(a±0.1, \;a±0.01, \;a±0.001, \;a±0.0001\), y así sucesivamente, y estos valores probablemente funcionarán casi siempre, en muy raras ocasiones es posible que necesitemos modificar nuestras elecciones).

3. Si ambas columnas se acercan a un\(y\) valor común\(L\), declaramos\(\displaystyle \lim_{x \to a}f(x)=L\). Podemos utilizar la siguiente estrategia para confirmar el resultado obtenido de la tabla o como método alternativo para estimar un límite.

4. Usando una calculadora gráfica o un software de computadora que nos permita funciones gráficas, podemos trazar la función\(f(x)\), asegurándonos que los valores funcionales de\(f(x)\) for\(x\) -values near\(a\) estén en nuestra ventana. Podemos usar la función de rastreo para movernos a lo largo de la gráfica de la función y observar la lectura\(y\) -value como el enfoque\(x\) -values\(a\). Si los\(y\) -valores\(L\) se acercan como nuestros\(x\) -valores se acercan\(a\) desde ambas direcciones, entonces\(\displaystyle \lim_{x \to a}f(x)=L\). Es posible que necesitemos acercar nuestra gráfica y repetir este proceso varias veces.

Aplicamos esta Estrategia de Resolución de Problemas para calcular un límite en Ejemplos\(\PageIndex{1A}\) y\(\PageIndex{1B}\).

Ejemplo\(\PageIndex{1A}\): Evaluating a Limit Using a Table of Functional Values

Evaluar\(\displaystyle \lim_{x \to 0}\frac{\sin x}{x}\) usando una tabla de valores funcionales.

Solución

Hemos calculado los valores de\(f(x)=\dfrac{\sin x}{x}\) para los valores de\(x\) enumerados en la Tabla\(\PageIndex{2}\).

Mesa\(\PageIndex{2}\)
\(x\)	\(\frac{\sin x}{x}\)	\(x\)	\(\frac{\sin x}{x}\)
\ (x\)” style="text-align:center; ">-0.1	\ (\ frac {\ sin x} {x}\)” style="text-align:center; ">0.998334166468	\ (x\)” style="text-align:center; ">0.1	\ (\ frac {\ sin x} {x}\)” style="text-align:center; ">0.998334166468
\ (x\)” style="text-align:center; ">-0.01	\ (\ frac {\ sin x} {x}\)” style="text-align:center; ">0.999983333417	\ (x\)” style="text-align:center; ">0.01	\ (\ frac {\ sin x} {x}\)” style="text-align:center; ">0.999983333417
\ (x\)” style="text-align:center; ">-0.001	\ (\ frac {\ sin x} {x}\)” style="text-align:center; ">0.999999833333	\ (x\)” style="text-align:center; ">0.001	\ (\ frac {\ sin x} {x}\)” style="text-align:center; ">0.999999833333
\ (x\)” style="text-align:center; ">-0.0001	\ (\ frac {\ sin x} {x}\)” style="text-align:center; ">0.9999998333	\ (x\)” style="text-align:center; ">0.0001	\ (\ frac {\ sin x} {x}\)” style="text-align:center; ">0.9999998333

Nota: Los valores de esta tabla se obtuvieron usando una calculadora y utilizando todos los lugares dados en la salida de la calculadora.

A medida que leemos cada\(\dfrac{\sin x}{x}\) columna, vemos que los valores en cada columna parecen estar acercándose a una. Por lo tanto, es bastante razonable concluir eso\(\displaystyle \lim_{x\to0}\frac{\sin x}{x}=1\). Una gráfica calculada o generada por computadora\(f(x)=\dfrac{\sin x}{x}\) sería similar a la que se muestra en la Figura\(\PageIndex{2}\), y confirma nuestra estimación.

Una gráfica de f (x) = sin (x) /x sobre el intervalo [-6, 6]. La función curvar tiene una intercepción y en x=0 y x intercepta en y=pi e y=-pi. — Figura\(\PageIndex{2}\): La gráfica de\(f(x)=(\sin x)/x\) confirma la estimación de la Tabla\(\PageIndex{2}\).

Ejemplo\(\PageIndex{1B}\): Evaluating a Limit Using a Table of Functional Values

Evaluar\(\displaystyle \lim_{x\to4}\frac{\sqrt{x}−2}{x−4}\) usando una tabla de valores funcionales.

Solución

Como antes, usamos una tabla—en este caso, Table\(\PageIndex{3}\) —para enumerar los valores de la función para los valores dados de\(x\).

Mesa\(\PageIndex{3}\)
\(x\)	\(\frac{\sqrt{x}−2}{x−4}\)	\(x\)	\(\frac{\sqrt{x}−2}{x−4}\)
\ (x\)” style="text-align:center; ">3.9	\ (\ frac {\ sqrt {x} −2} {x−4}\)” style="text-align:center; ">0.251582341869	\ (x\)” style="text-align:center; ">4.1	\ (\ frac {\ sqrt {x} −2} {x−4}\)” style="text-align:center; ">0.248456731317
\ (x\)” style="text-align:center; ">3.99	\ (\ frac {\ sqrt {x} −2} {x−4}\)” style="text-align:center; ">0.25015644562	\ (x\)” style="text-align:center; ">4.01	\ (\ frac {\ sqrt {x} −2} {x−4}\)” style="text-align:center; ">0.24984394501
\ (x\)” style="text-align:center; ">3.999	\ (\ frac {\ sqrt {x} −2} {x−4}\)” style="text-align:center; ">0.250015627	\ (x\)” style="text-align:center; ">4.001	\ (\ frac {\ sqrt {x} −2} {x−4}\)” style="text-align:center; ">0.249984377
\ (x\)” style="text-align:center; ">3.9999	\ (\ frac {\ sqrt {x} −2} {x−4}\)” style="text-align:center; ">0.250001563	\ (x\)” style="text-align:center; ">4.0001	\ (\ frac {\ sqrt {x} −2} {x−4}\)” style="text-align:center; ">0.249998438
\ (x\)” style="text-align:center; ">3.99999	\ (\ frac {\ sqrt {x} −2} {x−4}\)” style="text-align:center; ">0.25000016	\ (x\)” style="text-align:center; ">4.00001	\ (\ frac {\ sqrt {x} −2} {x−4}\)” style="text-align:center; ">0.24999984

Después de inspeccionar esta tabla, vemos que los valores funcionales menores a 4 parecen estar disminuyendo hacia 0.25 mientras que los valores funcionales mayores a 4 parecen estar aumentando hacia 0.25. Concluimos que\(\displaystyle \lim_{x\to4}\frac{\sqrt{x}−2}{x−4}=0.25\). Confirmamos esta estimación utilizando la gráfica que\(f(x)=\dfrac{\sqrt{x}−2}{x−4}\) se muestra en la Figura\(\PageIndex{3}\).

Una gráfica de la función f (x) = (sqrt (x) — 2)/(x-4) sobre el intervalo [0,8]. Hay un círculo abierto en la función en x=4. La función se curva asintóticamente hacia el eje x y el eje y en el cuadrante uno. — Figura\(\PageIndex{3}\): La gráfica de\(\frac{\sqrt{x}−2}{x−4}\) confirma la estimación de la Tabla\(\PageIndex{3}\).

Ejercicio\(\PageIndex{1}\)

Estimar\(\displaystyle \lim_{x \to 1} \frac{\frac{1}{x}−1}{x−1}\) usando una tabla de valores funcionales. Usa una gráfica para confirmar tu estimación.

Pista: Utilice 0.9, 0.99, 0.999, 0.9999, 0.99999 y 1.1, 1.01, 1.001, 1.0001, 1.00001 como valores de su tabla.
Contestar: \[\lim_{x\to1}\frac{\frac{1}{x}−1}{x−1}=−1\nonumber \]

En este punto, vemos a partir de Ejemplos\(\PageIndex{1A}\) y\(\PageIndex{1b}\) que puede ser igual de fácil, si no más fácil, estimar un límite de una función inspeccionando su gráfica como lo es estimar el límite usando una tabla de valores funcionales. En Ejemplo\(\PageIndex{2}\), evaluamos un límite exclusivamente mirando una gráfica en lugar de usar una tabla de valores funcionales.

Ejemplo\(\PageIndex{2}\): Evaluating a Limit Using a Graph

Para que\(g(x)\) se muestra en la Figura\(\PageIndex{4}\), evalúe\(\displaystyle \lim_{x\to−1}g(x)\).

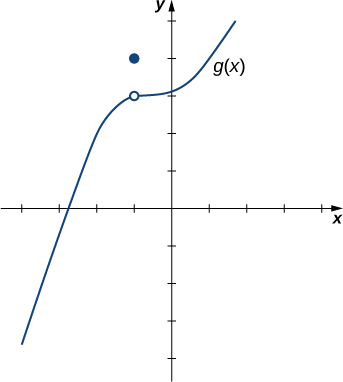
La gráfica de una función curva genérica g (x). En el cuadrante dos, hay un círculo abierto en la función en (-1,3) y un círculo cerrado una unidad hacia arriba en (-1, 4). — Figura\(\PageIndex{4}\): La gráfica de\(g(x)\) incluye un valor no en una curva suave.

Solución:

A pesar de que\(g(−1)=4\), a medida que los\(x\) -valores se acercan\(−1\) desde cualquier lado, los\(g(x)\) valores se acercan\(3\). Por lo tanto,\(\displaystyle \lim_{x\to−1}g(x)=3\). Tenga en cuenta que podemos determinar este límite sin siquiera conocer la expresión algebraica de la función.

Con base en Ejemplo\(\PageIndex{2}\), hacemos la siguiente observación: Es posible que el límite de una función exista en un punto, y que la función se defina en este punto, pero el límite de la función y el valor de la función en el punto pueden ser diferentes.

Ejercicio\(\PageIndex{2}\)

Utilice la gráfica de\(h(x)\) en la Figura\(\PageIndex{5}\) para evaluar\(\displaystyle \lim_{x \to 2}h(x)\), si es posible.

Una gráfica de la función h (x), que es una parábola graficada sobre [-2.5, 5]. Hay un círculo abierto donde el vértice debe estar en el punto (2, -1). — Figura\(\PageIndex{5}\):

Pista: ¿Qué\(y\) -valor se aproxima la función como el enfoque\(x\) -valores\(2\)?
Solución: \(\displaystyle \lim_{x \to 2}h(x)=−1.\)

Mirar una tabla de valores funcionales o mirar la gráfica de una función nos proporciona una visión útil del valor del límite de una función en un punto dado. Sin embargo, estas técnicas se basan demasiado en conjeturas. Eventualmente necesitamos desarrollar métodos alternativos de evaluación de límites. Estos nuevos métodos son de naturaleza más algebraica y los exploramos en la siguiente sección; sin embargo, en este punto introducimos dos límites especiales que son fundamentales para las técnicas por venir.

Dos límites importantes

\(a\)Sea un número real y\(c\) sea una constante.

\(\displaystyle \lim_{x \to a}x=a\)
\(\displaystyle \lim_{x \to a}c=c\)

Podemos hacer las siguientes observaciones sobre estos dos límites.

Para el primer límite, observar que a medida que se\(x\) aproxima\(a\), también lo hace\(f(x)\), porque\(f(x)=x\). En consecuencia,\(\displaystyle \lim_{x \to a}x=a\).
Para el segundo límite, considere Tabla\(\PageIndex{4}\).

Mesa\(\PageIndex{4}\)
\(x\)	\(f(x)=c\)	\(x\)	\(f(x)=c\)
\ (x\)” style="text-align:center; ">\(a-0.1\)	\ (f (x) =c\)” style="text-align:center; ">\(c\)	\ (x\)” style="text-align:center; ">\(a+0.1\)	\ (f (x) =c\)” style="text-align:center; ">\(c\)
\ (x\)” style="text-align:center; ">\(a-0.01\)	\ (f (x) =c\)” style="text-align:center; ">\(c\)	\ (x\)” style="text-align:center; ">\(a+0.01\)	\ (f (x) =c\)” style="text-align:center; ">\(c\)
\ (x\)” style="text-align:center; ">\(a-0.001\)	\ (f (x) =c\)” style="text-align:center; ">\(c\)	\ (x\)” style="text-align:center; ">\(a+0.001\)	\ (f (x) =c\)” style="text-align:center; ">\(c\)
\ (x\)” style="text-align:center; ">\(a-0.0001\)	\ (f (x) =c\)” style="text-align:center; ">\(c\)	\ (x\)” style="text-align:center; ">\(a+0.0001\)	\ (f (x) =c\)” style="text-align:center; ">\(c\)

Observe que para todos los valores de\(x\) (independientemente de si se acercan\(a\)), los valores\(f(x)\) permanecen constantes en\(c\). No tenemos más remedio que concluir\(\displaystyle \lim_{x \to a}c=c\).

La existencia de un límite

Al considerar el límite en el siguiente ejemplo, hay que tener en cuenta que para que el límite de una función exista en un punto, los valores funcionales deben acercarse a un único valor de número real en ese punto. Si los valores funcionales no se acercan a un solo valor, entonces el límite no existe.

Ejemplo\(\PageIndex{3}\): Evaluating a Limit That Fails to Exist

Evaluar\(\displaystyle\lim_{x \to 0}\sin(1/x)\) usando una tabla de valores.

Solución

Tabla\(\PageIndex{5}\) enumera los valores para la función\(\sin(1/x)\) para los valores dados de\(x\).

Mesa\(\PageIndex{5}\)
\(x\)	\(\sin(1/x)\)	\(x\)	\(\sin(1/x)\)
\ (x\)” style="text-align:center; ">-0.1	\ (\ sin (1/x)\)” style="text-align:center; ">0.544021110889	\ (x\)” style="text-align:center; ">0.1	\ (\ sin (1/x)\)” style="text-align:center; ">−0.544021110889
\ (x\)” style="text-align:center; ">-0.01	\ (\ sin (1/x)\)” style="text-align:center; ">0.50636564111	\ (x\)” style="text-align:center; ">0.01	\ (\ sin (1/x)\)” style="text-align:center; ">−0.50636564111
\ (x\)” style="text-align:center; ">-0.001	\ (\ sin (1/x)\)” style="text-align:center; ">−0.8268795405312	\ (x\)” style="text-align:center; ">0.001	\ (\ sin (1/x)\)” style="text-align:center; ">0.8268795405312
\ (x\)” style="text-align:center; ">-0.0001	\ (\ sin (1/x)\)” style="text-align:center; ">0.305614388888	\ (x\)” style="text-align:center; ">0.0001	\ (\ sin (1/x)\)” style="text-align:center; ">−0.305614388888
\ (x\)” style="text-align:center; ">-0.00001	\ (\ sin (1/x)\)” style="text-align:center; ">−0.035748797987	\ (x\)” style="text-align:center; ">0.00001	\ (\ sin (1/x)\)” style="text-align:center; ">0.035748797987
\ (x\)” style="text-align:center; ">-0.000001	\ (\ sin (1/x)\)” style="text-align:center; ">0.349993504187	\ (x\)” style="text-align:center; ">0.000001	\ (\ sin (1/x)\)” style="text-align:center; ">−0.349993504187

Después de examinar la tabla de valores funcionales, podemos ver que los\(y\) -valores no parecen acercarse a ningún valor único. Parece que el límite no existe. Antes de sacar esta conclusión, tomemos un enfoque más sistemático. Tome la siguiente secuencia\(x\) de valores aproximándose\(0\):

\[\frac{2}{π},\;\frac{2}{3π},\;\frac{2}{5π},\;\frac{2}{7π},\;\frac{2}{9π},\;\frac{2}{11π},\;….\nonumber \]

Los\(y\) valores correspondientes son

\[1,\;-1,\;1,\;-1,\;1,\;-1,\;....\nonumber \]

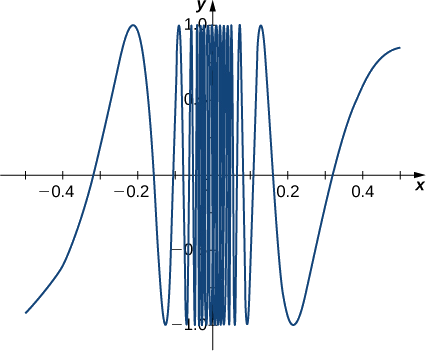
En este punto efectivamente podemos concluir que eso\(\displaystyle \lim_{x \to 0} \sin(1/x)\) no existe. (Los matemáticos frecuentemente abrevian “no existe” como DNE. Así, escribiríamos\(\displaystyle \lim_{x \to 0} \sin(1/x)\) DNE.) La gráfica de\(f(x)=\sin(1/x)\) se muestra en la Figura\(\PageIndex{6}\) y da una imagen más clara del comportamiento de a\(\sin(1/x)\) medida que se\(x\) aproxima\(0\). Se puede ver que\(\sin(1/x)\) oscila cada vez más salvajemente entre\(−1\) y\(1\) como\(x\) enfoques\(0\).

El gráfico de la función f (x) = sin (1/x), que oscila rápidamente entre -1 y 1 a medida que x se acerca a 0. Las oscilaciones son menos frecuentes ya que la función se aleja de 0 en el eje x. — Figura\(\PageIndex{6}\): La gráfica de\(f(x)=\sin (1/x)\) oscila rápidamente entre\(−1\) y a\(1\) medida que se\(x\) aproxima\(0\).

Ejercicio\(\PageIndex{3}\)

Utilice una tabla de valores funcionales para evaluar\(\displaystyle \lim_{x \to 2}\frac{∣x^2−4∣}{x−2}\), si es posible.

Pista: Utilice\(x\) -valores 1.9, 1.99, 1.999, 1.9999, 1.99999 y 2.1, 2.01, 2.001, 2.0001, 2.00001 en su tabla.
Contestar: \(\displaystyle \lim_{x \to 2}\frac{∣x^2−4∣}{x−2}\)no existe.

Límites unilaterales

En ocasiones indicar que el límite de una función no existe en un punto no nos proporciona suficiente información sobre el comportamiento de la función en ese punto en particular. Para ver esto, ahora volvemos a visitar la función\(g(x)=|x−2|/(x−2)\) introducida al inicio de la sección (ver Figura\(\PageIndex{1}\) (b)). A medida que elegimos valores\(x\) cercanos a\(2\),\(g(x)\) no se acerca a un solo valor, por lo que el límite como\(x\) enfoques\(2\) no existe, es decir, el\(\displaystyle \lim_{x \to 2}g(x)\) DNE. Sin embargo, esta afirmación por sí sola no nos da una imagen completa del comportamiento de la función alrededor del\(x\) -value\(2\). Para proporcionar una descripción más precisa, presentamos la idea de un límite unilateral. Para todos los valores a la izquierda de\(2\) (o el lado negativo de\(2\)),\(g(x)=−1\). Así, a medida que\(x\) se\(2\) aproxima desde la izquierda,\(g(x)\) se acerca\(−1\). Matemáticamente, decimos que el límite a medida que se\(x\)\(2\) aproxima desde la izquierda es\(−1\). Simbólicamente, expresamos esta idea como

\[\lim_{x \to 2^−}g(x)=−1. \nonumber \]

De igual manera, como\(x\) enfoques\(2\) desde la derecha (o desde el lado positivo),\(g(x)\) se acerca\(1\). Simbólicamente, expresamos esta idea como

\[\lim_{x \to 2^+}g(x)=1.\nonumber \]

Ahora podemos presentar una definición informal de límites unilaterales.

Definición: Límites unilaterales

Definimos dos tipos de límites unilaterales.

Límite desde la izquierda:

Dejar\(f(x)\) ser una función definida en todos los valores en un intervalo abierto de la forma\((z,a)\), y dejar\(L\) ser un número real. Si los valores de la función se\(f(x)\) acercan al número real a\(L\) medida que los valores de\(x\) (donde\(x<a\)) se acercan al número\(a\), entonces decimos que\(L\) es el límite de\(f(x)\) como se\(x\) acerca\(a\) desde la izquierda. Simbólicamente, expresamos esta idea como

\[\lim_{x \to a^−}f(x)=L. \nonumber \]

Límite desde la derecha:

Dejar\(f(x)\) ser una función definida en todos los valores en un intervalo abierto de la forma\((a,c)\), y dejar\(L\) ser un número real. Si los valores de la función se\(f(x)\) acercan al número real a\(L\) medida que los valores de\(x\) (donde\(x>a\)) se acercan al número\(a\), entonces decimos que\(L\) es el límite de\(f(x)\) como se\(x\) acerca\(a\) desde la derecha. Simbólicamente, expresamos esta idea como

\[\lim_{x \to a^+}f(x)=L. \nonumber \]

Ejemplo\(\PageIndex{4}\): Evaluating One-Sided Limits

Para la función\(f(x)=\begin{cases}x+1, & \text{if }x<2\\ x^2−4, & \text{if }x≥2\end{cases}\), evalúe cada uno de los siguientes límites.

\(\displaystyle \lim_{x \to 2^−}f(x)\)
\(\displaystyle \lim_{x \to 2^+}f(x)\)

Solución

Podemos volver a utilizar tablas de valores funcionales. Observe en Tabla\(\PageIndex{6}\) que para valores\(x\) menores que\(2\), usamos\(f(x)=x+1\) y para valores\(x\) mayores que\(2\), usamos\(f(x)=x^2−4.\)

Mesa\(\PageIndex{6}\)
\(x\)	\(f(x)=x+1\)	\(x\)	\(f(x)=x^2-4\)
\ (x\)” style="text-align:center; ">1.9	\ (f (x) =x+1\)” style="text-align:center; ">2.9	\ (x\)” style="text-align:center; ">2.1	\ (f (x) =x^2-4\)” style="text-align:center; ">0.41
\ (x\)” style="text-align:center; ">1.99	\ (f (x) =x+1\)” style="text-align:center; ">2.99	\ (x\)” style="text-align:center; ">2.01	\ (f (x) =x^2-4\)” style="text-align:center; ">0.0401
\ (x\)” style="text-align:center; ">1.999	\ (f (x) =x+1\)” style="text-align:center; ">2.999	\ (x\)” style="text-align:center; ">2.001	\ (f (x) =x^2-4\)” style="text-align:center; ">0.004001
\ (x\)” style="text-align:center; ">1.9999	\ (f (x) =x+1\)” style="text-align:center; ">2.9999	\ (x\)” style="text-align:center; ">2.0001	\ (f (x) =x^2-4\)” style="text-align:center; ">0.00040001
\ (x\)” style="text-align:center; ">1.99999	\ (f (x) =x+1\)” style="text-align:center; ">2.99999	\ (x\)” style="text-align:center; ">2.00001	\ (f (x) =x^2-4\)” style="text-align:center; ">0.0000400001

Con base en esta tabla, podemos concluir que a.\(\displaystyle \lim_{x \to 2^−}f(x)=3\) y b\(\displaystyle \lim_{x \to 2^+}f(x)=0\). Por lo tanto, el límite (de dos caras) de\(f(x)\) no existe en\(x=2\). La figura\(\PageIndex{7}\) muestra una gráfica de estos límites\(f(x)\) y refuerza nuestra conclusión sobre estos límites.

La gráfica de la función por tramos dada. La primera pieza es f (x) = x+1 si x < 2. La segunda pieza es x^2 — 4 si x — Figura\(\PageIndex{7}\): La gráfica de\(f(x)=\begin{cases}x+1, & \text{if }x<2\\ x^2−4, & \text{if }x≥2\end{cases}\) tiene una ruptura en\(x=2\).

Ejercicio\(\PageIndex{4}\)

Utilice una tabla de valores funcionales para estimar los siguientes límites, si es posible.

\(\displaystyle \lim_{x→2^−}\frac{∣x^2−4∣}{x−2}\)
\(\displaystyle \lim_{x→2^+}\frac{∣x^2−4∣}{x−2}\)

Pista

Utilice\(x\) -valores 1.9, 1.99, 1.999, 1.9999, 1.99999 para estimar\(\displaystyle \lim_{x→2^−}\frac{∣x^2−4∣}{x−2}\).

Utilice\(x\) -valores 2.1, 2.01, 2.001, 2.0001, 2.00001 para estimar\(\displaystyle \lim_{x→2^+}\frac{∣x^2−4∣}{x−2}.\)

(Estas tablas están disponibles a partir de un problema de Checkpoint anterior).

Solución a

a.\(\displaystyle \lim_{x→2^−}\frac{∣x^2−4∣}{x−2}=−4\)

Solución b

\(\displaystyle \lim_{x→2^+}\frac{∣x^2−4∣}{x−2}=4\)

Consideremos ahora la relación entre el límite de una función en un punto y los límites de derecha e izquierda en ese punto. Parece claro que si el límite de la derecha y el límite de la izquierda tienen un valor común, entonces ese valor común es el límite de la función en ese punto. De igual manera, si el límite de la izquierda y el límite de la derecha toman diferentes valores, el límite de la función no existe. Estas conclusiones se resumen en Nota.

Relacionar los límites de una cara y de dos caras

Dejar\(f(x)\) ser una función definida en todos los valores en un intervalo abierto conteniendo\(a\), con la posible excepción de\(a\) sí misma, y dejar\(L\) ser un número real. Entonces,

\[\lim_{x \to a}f(x)=L \nonumber \]

si y sólo si\(\displaystyle \lim_{x \to a^−}f(x)=L\) y\(\displaystyle \lim_{x \to a^+} f(x)=L\).

Límites Infinitos

Evaluar el límite de una función en un punto o evaluar el límite de una función desde la derecha y la izquierda en un punto nos ayuda a caracterizar el comportamiento de una función alrededor de un valor dado. Como veremos, también podemos describir el comportamiento de funciones que no tienen límites finitos.

Pasamos ahora nuestra atención a\(h(x)=1/(x−2)^2\), la tercera y última función introducida al inicio de esta sección (ver Figura\(\PageIndex{1}\) (c)). De su gráfica vemos que a medida que los valores de\(x\) aproximación\(2\), los valores de\(h(x)=1/(x−2)^2\) se hacen cada vez más grandes y, de hecho, se vuelven infinitos. Matemáticamente, decimos que el límite de\(h(x)\) como\(2\) se\(x\) acerca es el infinito positivo. Simbólicamente, expresamos esta idea como

\[\lim_{x \to 2}h(x)=+∞. \nonumber \]

De manera más general, definimos límites infinitos de la siguiente manera:

Definiciones: Límites infinitos

Definimos tres tipos de límites infinitos.

Límites infinitos desde la izquierda: Dejar\(f(x)\) ser una función definida en todos los valores en un intervalo abierto de la forma\((b,a)\).

i. Si los valores de\(f(x)\) incremento sin límite como los valores de\(x\) (donde\(x<a\)) se acercan al número\(a\), entonces decimos que el límite como se\(x\) acerca\(a\) desde la izquierda es infinito positivo y escribimos\[\lim_{x \to a^−}f(x)=+∞. \nonumber \]

ii. Si los valores de\(f(x)\) disminución sin límite como los valores de\(x\) (donde\(x<a\)) se acercan al número\(a\), entonces decimos que el límite como se\(x\) acerca\(a\) desde la izquierda es infinito negativo y escribimos\[\lim_{x \to a^−}f(x)=−∞. \nonumber \]

Límites infinitos desde la derecha: Dejar\(f(x)\) ser una función definida en todos los valores en un intervalo abierto de la forma\((a,c)\).

i. Si los valores de\(f(x)\) incremento sin límite como los valores de\(x\) (donde\(x>a\)) se acercan al número\(a\), entonces decimos que el límite como se\(x\) acerca\(a\) desde la derecha es infinito positivo y escribimos\[\lim_{x \to a^+}f(x)=+∞. \nonumber \]

ii. Si los valores de\(f(x)\) disminución sin límite como los valores de\(x\) (donde\(x>a\)) se acercan al número\(a\), entonces decimos que el límite como se\(x\) acerca\(a\) desde la derecha es infinito negativo y escribimos\[\lim_{x \to a^+}f(x)=−∞. \nonumber \]

Límite infinito de dos caras: Dejar\(f(x)\) ser definido para todos\(x≠a\) en un intervalo abierto que contiene\(a\)

i. Si los valores de\(f(x)\) incremento sin límite como los valores de\(x\) (donde\(x≠a\)) se acercan al número\(a\), entonces decimos que el límite como\(a\) se\(x\) acerca es infinito positivo y escribimos\[\lim_{x \to a} f(x)=+∞. \nonumber \]

ii. Si los valores de\(f(x)\) disminución sin límite como los valores de\(x\) (donde\(x≠a\)) se acercan al número\(a\), entonces decimos que el límite como\(a\) se\(x\) acerca es infinito negativo y escribimos\[\lim_{x \to a}f(x)=−∞. \nonumber \]

Es importante entender que cuando escribimos declaraciones como\(\displaystyle \lim_{x \to a}f(x)=+∞\) o\(\displaystyle \lim_{x \to a}f(x)=−∞\) estamos describiendo el comportamiento de la función, como la acabamos de definir. No estamos afirmando que exista un límite. Para que el límite de una función exista en\(a\), debe acercarse\(f(x)\) a un número real a\(L\) medida que\(x\) se acerca\(a\). Dicho esto, si, por ejemplo\(\displaystyle \lim_{x \to a}f(x)=+∞\), siempre escribimos\(\displaystyle \lim_{x \to a}f(x)=+∞\) más que\(\displaystyle \lim_{x \to a}f(x)\) DNE.

Ejemplo\(\PageIndex{5}\): Recognizing an Infinite Limit

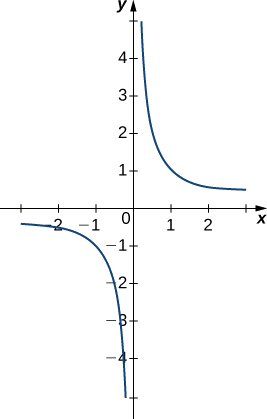
Evaluar cada uno de los siguientes límites, si es posible. Utilice una tabla de valores funcionales y una gráfica\(f(x)=1/x\) para confirmar su conclusión.

\(\displaystyle \lim_{x \to 0^−} \frac{1}{x}\)
\(\displaystyle \lim_{x \to 0^+} \frac{1}{x}\)
\( \displaystyle \lim_{x \to 0}\frac{1}{x}\)

Solución

Comience por construir una tabla de valores funcionales.

Mesa\(\PageIndex{7}\)
\(x\)	\(\dfrac{1}{x}\)	\(x\)	\(\dfrac{1}{x}\)
\ (x\)” style="text-align:center; ">-0.1	\ (\ dfrac {1} {x}\)” style="text-align:center; ">-10	\ (x\)” style="text-align:center; ">0.1	\ (\ dfrac {1} {x}\)” style="text-align:center; ">10
\ (x\)” style="text-align:center; ">-0.01	\ (\ dfrac {1} {x}\)” style="text-align:center; ">-100	\ (x\)” style="text-align:center; ">0.01	\ (\ dfrac {1} {x}\)” style="text-align:center; ">100
\ (x\)” style="text-align:center; ">-0.001	\ (\ dfrac {1} {x}\)” style="text-align:center; ">-1000	\ (x\)” style="text-align:center; ">0.001	\ (\ dfrac {1} {x}\)” style="text-align:center; ">1000
\ (x\)” style="text-align:center; ">-0.0001	\ (\ dfrac {1} {x}\)” style="text-align:center; ">-10,000	\ (x\)” style="text-align:center; ">0.0001	\ (\ dfrac {1} {x}\)” style="text-align:center; ">10,000
\ (x\)” style="text-align:center; ">-0.00001	\ (\ dfrac {1} {x}\)” style="text-align:center; ">-100,000	\ (x\)” style="text-align:center; ">0.00001	\ (\ dfrac {1} {x}\)” style="text-align:center; ">100,000
\ (x\)” style="text-align:center; ">-0.000001	\ (\ dfrac {1} {x}\)” style="text-align:center; ">-1.000.000	\ (x\)” style="text-align:center; ">0.000001	\ (\ dfrac {1} {x}\)” style="text-align:center; ">1.000.000

a. Los valores de\(1/x\) disminución sin límite como\(x\) aproximaciones\(0\) desde la izquierda. Concluimos que

\[\lim_{x \to 0^−}\frac{1}{x}=−∞.\nonumber \]

b. Los valores de\(1/x\) incremento sin encuadernación como\(x\) aproximaciones\(0\) desde la derecha. Concluimos que

\[\lim_{x \to 0^+}\frac{1}{x}=+∞. \nonumber \]

c. Dado que\(\displaystyle \lim_{x \to 0^−}\frac{1}{x}=−∞\) y\(\displaystyle \lim_{x \to 0^+}\frac{1}{x}=+∞\) tienen valores diferentes, concluimos que

\[\lim_{x \to 0}\frac{1}{x}\quad\text{DNE.} \nonumber \]

La gráfica de\(f(x)=1/x\) en la Figura\(\PageIndex{8}\) confirma estas conclusiones.

La gráfica de la función f (x) = 1/x La función se curva asintóticamente hacia x=0 e y=0 en los cuadrantes uno y tres. — Figura\(\PageIndex{8}\): La gráfica de\(f(x)=1/x\) confirma que el límite como\(x\) aproximaciones\(0\) no existe.

Ejercicio\(\PageIndex{5}\)

Evaluar cada uno de los siguientes límites, si es posible. Utilice una tabla de valores funcionales y una gráfica\(f(x)=1/x^2\) para confirmar su conclusión.

\(\displaystyle \lim_{x \to 0^−}\frac{1}{x^2}\)
\(\displaystyle \lim_{x \to 0^+}\frac{1}{x^2}\)
\(\displaystyle \lim_{x \to 0}\frac{1}{x^2}\)

Pista

Siga los procedimientos de Ejemplo\(\PageIndex{5}\).

Contestar

a.\(\displaystyle \lim_{x \to 0^−}\frac{1}{x^2}=+∞\);

b.\(\displaystyle \lim_{x \to 0^+}\frac{1}{x^2}=+∞\);

c.\(\displaystyle \lim_{x \to 0}\frac{1}{x^2}=+∞\)

Es útil señalar que las funciones de la forma\(f(x)=1/(x−a)^n\), donde n es un entero positivo, tienen límites infinitos como\(x\) aproximaciones ya sea\(a\) desde la izquierda o desde la derecha (Figura\(\PageIndex{9}\)). Estos límites se resumen en las definiciones anteriores.

Dos gráficas lado a lado de f (x) = 1/(x-a) ^n La primera gráfica muestra el caso donde n es un entero positivo impar, y el segundo muestra el caso donde n es un entero positivo par. En la primera, la gráfica tiene dos segmentos. Cada curva asintóticamente hacia el eje x, también conocida como y=0 y x=a, el segmento a la izquierda de x=a está debajo del eje x, y el segmento a la derecha de x=a está por encima del eje x. En la segunda gráfica, ambos segmentos están por encima del eje x. — Figura\(\PageIndex{9}\): La función\(f(x)=1/(x−a)^n\) tiene límites infinitos en\(a\).

Límites infinitos a partir de enteros positivos

Si\(n\) es un entero par positivo, entonces

\[\lim_{x \to a}\frac{1}{(x−a)^n}=+∞.\label{infLim1} \]

Si\(n\) es un entero impar positivo, entonces

\[\lim_{x \to a^+}\frac{1}{(x−a)^n}=+∞\label{infLim2} \]

\[\lim_{x \to a^−}\frac{1}{(x−a)^n}=−∞.\label{infLim3} \]

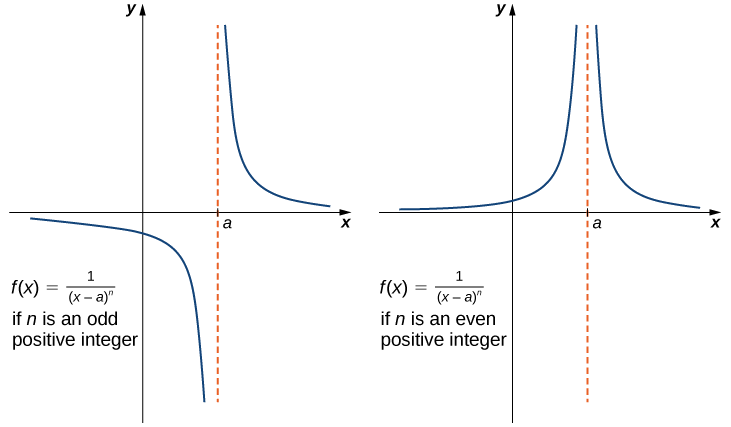
También hay que señalar que en las gráficas de\(f(x)=1/(x−a)^n\), los puntos en la gráfica que tienen\(x\) -coordenadas muy cercanas a\(a\) están muy cerca de la línea vertical\(x=a\). Es decir, a medida que\(x\) se aproxima\(a\), los puntos en la gráfica de\(f(x)\) están más cerca de la línea\(x=a\). La línea\(x=a\) se llama asíntota vertical de la gráfica. Formalmente definimos una asíntota vertical de la siguiente manera:

Definición: Asíntotas Verticales

Dejar\(f(x)\) ser una función. Si alguna de las siguientes condiciones se mantiene, entonces la línea\(x=a\) es una asíntota vertical de\(f(x)\).

\[\lim_{x \to a^−}f(x)=+∞ \nonumber \]

\[\lim_{x \to a^−}f(x)=−∞ \nonumber \]

\[\lim_{x \to a^+}f(x)=+∞ \nonumber \]

\[\lim_{x \to a^+}f(x)=−∞ \nonumber \]

\[\lim_{x \to a}f(x)=+∞ \nonumber \]

\[\lim_{x \to a}f(x)=−∞ \nonumber \]

Ejemplo\(\PageIndex{6}\): Finding a Vertical Asymptote

Evalúe cada uno de los siguientes límites usando las ecuaciones\ ref {inflim1},\ ref {inflim2} y\ ref {inflim3} anteriores. Identificar cualquier asíntota vertical de la función\(f(x)=1/(x+3)^4.\)

\(\displaystyle \lim_{x \to −3^−}\frac{1}{(x+3)^4}\)
\(\displaystyle \lim_{x \to −3^+}\frac{1}{(x+3)^4}\)
\(\displaystyle \lim_{x \to −3}\frac{1}{(x+3)^4}\)

Solución

Podemos usar directamente las ecuaciones anteriores.

\(\displaystyle \lim_{x \to −3^−}\frac{1}{(x+3)^4}=+∞\)
\(\displaystyle \lim_{x \to −3^+}\frac{1}{(x+3)^4}=+∞\)
\(\displaystyle \lim_{x \to −3}\frac{1}{(x+3)^4}=+∞\)

La función\(f(x)=1/(x+3)^4\) tiene una asíntota vertical de\(x=−3\).

Ejercicio\(\PageIndex{6}\)

Evaluar cada uno de los siguientes límites. Identificar cualquier asíntota vertical de la función\(f(x)=\dfrac{1}{(x−2)^3}\).

\(\displaystyle \lim_{x→2^−}\frac{1}{(x−2)^3}\)
\(\displaystyle \lim_{x→2^+}\frac{1}{(x−2)^3}\)
\(\displaystyle \lim_{x→2}\frac{1}{(x−2)^3}\)

Contestar a: \(\displaystyle \lim_{x→2^−}\frac{1}{(x−2)^3}=−∞\)
Respuesta b: \(\displaystyle \lim_{x→2^+}\frac{1}{(x−2)^3}=+∞\)
Respuesta c: \(\displaystyle \lim_{x→2}\frac{1}{(x−2)^3}\)DNE. La línea\(x=2\) es la asíntota vertical de\(f(x)=1/(x−2)^3.\)

En el siguiente ejemplo ponemos nuestro conocimiento de diversos tipos de límites a utilizar para analizar el comportamiento de una función en varios puntos diferentes.

Ejemplo\(\PageIndex{7}\): Behavior of a Function at Different Points

Utilice la gráfica de\(f(x)\) la Figura\(\PageIndex{10}\) para determinar cada uno de los siguientes valores:

\(\displaystyle \lim_{x \to −4^−}f(x)\);\(\displaystyle \lim_{x \to −4^+}f(x)\);\(\displaystyle \lim_{x→−4}f(x);\;f(−4)\)
\(\displaystyle \lim_{x \to −2^−}f(x\));\(\displaystyle \lim_{x \to −2^+}f(x)\);\(\displaystyle \lim_{x→−2}f(x);\;f(−2)\)
\( \displaystyle \lim_{x \to 1^−}f(x)\);\(\displaystyle \lim_{x \to 1^+}f(x)\);\(\displaystyle \lim_{x \to 1}f(x);\;f(1)\)
\( \displaystyle \lim_{x \to 3^−}f(x)\);\(\displaystyle \lim_{x \to 3^+}f(x)\);\(\displaystyle \lim_{x \to 3}f(x);\;f(3)\)

La gráfica de una función f (x) descrita por los límites y valores anteriores. Hay una curva suave para valores por debajo de x=-2; en (-2, 3), hay un círculo abierto. Hay una curva suave entre (-2, 1] con un círculo cerrado en (1,6). Hay un círculo abierto en (1,3), y una curva suave que se extiende desde allí hacia abajo asintóticamente hasta el infinito negativo a lo largo de x=3. La función también se curva asintóticamente a lo largo de x=3 en el otro lado, extendiéndose también hasta el infinito negativo. La función luego cambia la concavidad en el primer cuadrante alrededor de y=4.5 y continúa hacia arriba. — Figura\(\PageIndex{10}\): La gráfica muestra\(f(x)\).

Solución

Usando las definiciones anteriores y la gráfica para referencia, llegamos a los siguientes valores:

\(\displaystyle \lim_{x \to −4^−}f(x)=0\);\(\displaystyle \lim_{x \to −4^+}f(x)=0\);\(\displaystyle \lim_{x \to −4}f(x)=0;\;f(−4)=0\)
\(\displaystyle \lim_{x \to −2^−}f(x)=3\);\(\displaystyle \lim_{x \to −2^+}f(x)=3\); no\(\displaystyle \lim_{x \to −2}f(x)=3;\;f(−2)\) está definido
\(\displaystyle \lim_{x \to 1^−}f(x)=6\);\(\displaystyle \lim_{x \to 1^+}f(x)=3\);\(\displaystyle \lim_{x \to 1}f(x)\) DNE;\(f(1)=6\)
\(\displaystyle \lim_{x \to 3^−}f(x)=−∞\);\(\displaystyle \lim_{x \to 3^+}f(x)=−∞\);\(\displaystyle \lim_{x \to 3}f(x)=−∞\); no\(f(3)\) está definido

Ejercicio\(\PageIndex{7}\)

Evaluar\(\displaystyle\lim_{x \to 1}f(x)\) para\(f(x)\) se muestra aquí:

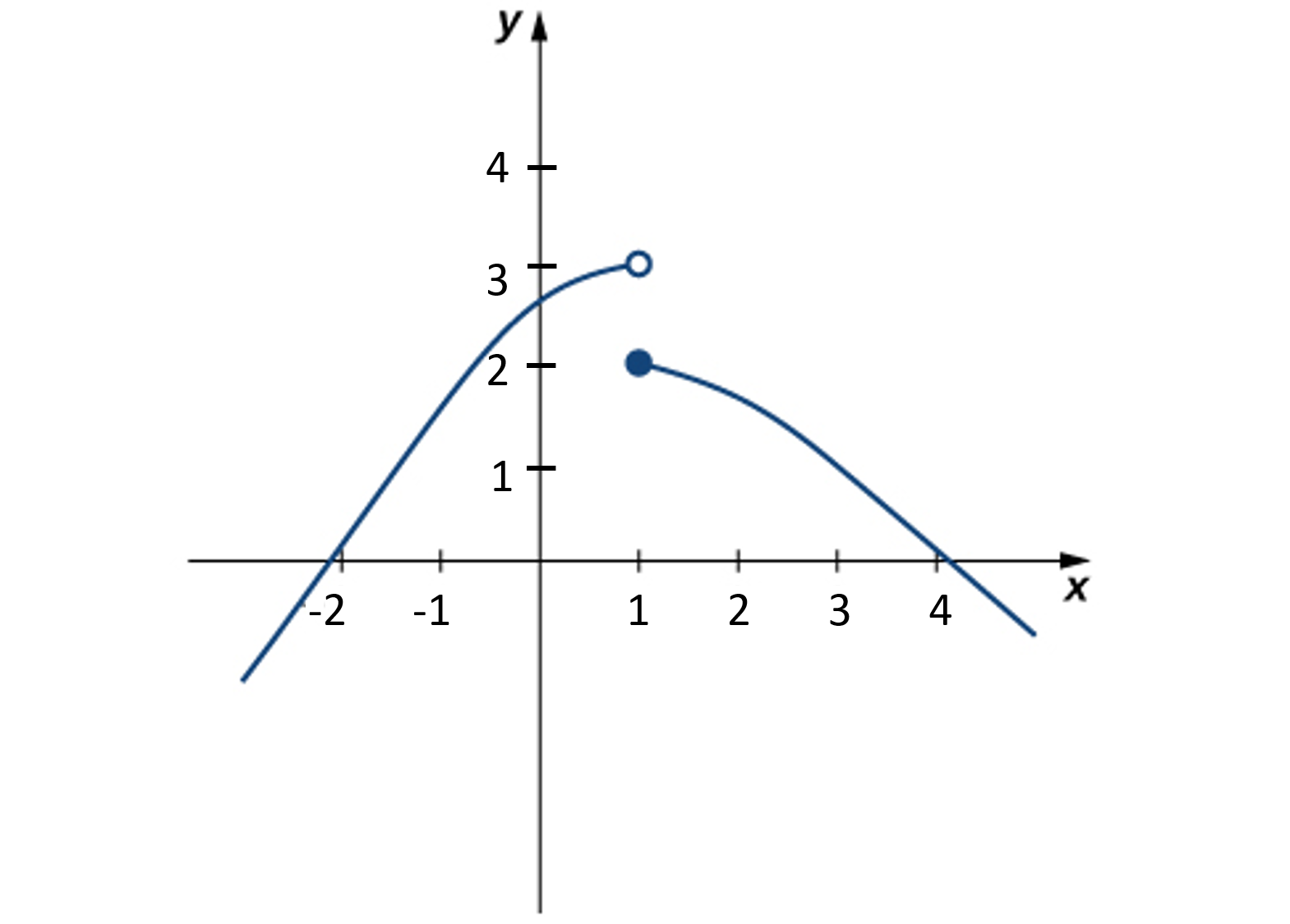
La gráfica de una función por partes. El primer segmento se curva desde el tercer cuadrante hasta el primero, cruzando por el segundo cuadrante. Donde el punto final estaría en el primer cuadrante es un círculo abierto. El segundo segmento inicia en un círculo cerrado unas pocas unidades por debajo del círculo abierto. Se curva hacia abajo del cuadrante uno al cuadrante cuatro. — Figura\(\PageIndex{11}\). La gráfica de una función por tramos\(f\).

Pista: Compara el límite de la derecha con el límite de la izquierda.
Contestar: \(\displaystyle\lim_{x \to 1}f(x)\)no existe

Ejemplo\(\PageIndex{8}\): Einstein’s Equation

En el abridor del Capítulo mencionamos brevemente cómo Albert Einstein demostró que existe un límite a la rapidez con que puede viajar cualquier objeto. Dada la ecuación de Einstein para la masa de un objeto en movimiento

\[m=\dfrac{m_0}{\sqrt{1−\frac{v^2}{c^2}}}, \nonumber \]

¿Cuál es el valor de esta encuadernación?

Una imagen de una nave espacial futurista acelerando a través del espacio profundo. — Figura\(\PageIndex{12}\). (Crédito:NASA)

Solución

Nuestro punto de partida es la ecuación de Einstein para la masa de un objeto en movimiento,

\[m=\dfrac{m_0}{\sqrt{1−\frac{v^2}{c^2}}}, \nonumber \]

donde\(m_0\) está la masa del objeto en reposo,\(v\) es su velocidad, y\(c\) es la velocidad de la luz. Para ver cómo cambia la masa a altas velocidades, podemos graficar la relación de masas\(m/m_0\) en función de la relación de velocidades,\(v/c\) (Figura\(\PageIndex{13}\)).

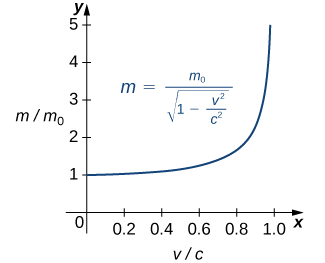
Un gráfico que muestra la relación de masas en función de la relación de velocidad en la ecuación de Einstein para la masa de un objeto en movimiento. El eje x es la relación de las velocidades, v/c. el eje y es la relación de las masas, m/m0. La ecuación de la función es m = m0/sqrt (1 — v2/c2). El gráfico sólo está en el cuadrante 1. Comienza en (0,1) y se curva suavemente hasta aproximadamente 0.8, donde aumenta aparentemente exponencialmente; hay una asíntota vertical a v/c (o x) = 1. — Figura\(\PageIndex{13}\): Esta gráfica muestra la relación de masas en función de la relación de velocidades en la ecuación de Einstein para la masa de un objeto en movimiento.

Podemos ver que a medida que la relación de velocidades se acerca 1—es decir, a medida que la velocidad del objeto se acerca a la velocidad de la luz, la relación de masas aumenta sin límite. En otras palabras, la función tiene una asíntota vertical en\(v/c=1\). Podemos probar algunos valores de esta relación para poner a prueba esta idea.

Mesa\(\PageIndex{8}\)
\(v/c\)	\(\sqrt{1-\frac{v^2}{c^2}}\)	\(m/m_o\)
\ (v/c\)” style="text-align:center; ">0.99	\ (\ sqrt {1-\ frac {v^2} {c^2}}\)” style="text-align:center; ">0.1411	\ (m/m_o\)” style="text-align:center; ">7.089
\ (v/c\)” style="text-align:center; ">0.999	\ (\ sqrt {1-\ frac {v^2} {c^2}}\)” style="text-align:center; ">0.0447	\ (m/m_o\)” style="text-align:center; ">22.37
\ (v/c\)” style="text-align:center; ">0.9999	\ (\ sqrt {1-\ frac {v^2} {c^2}}\)” style="text-align:center; ">0.0141	\ (m/m_o\)” style="text-align:center; ">70.7

Así, de acuerdo con la Tabla\(\PageIndex{8}\):, si un objeto con masa de 100 kg viaja a 0.9999c, su masa se convierte en 7071 kg. Como ningún objeto puede tener una masa infinita, concluimos que ningún objeto puede viajar a o más que la velocidad de la luz.

Conceptos clave

Se puede utilizar una tabla de valores o gráfica para estimar un límite.
Si el límite de una función en un punto no existe, aún es posible que existan los límites de izquierda y derecha en ese punto.
Si los límites de una función desde la izquierda y la derecha existen y son iguales, entonces el límite de la función es ese valor común.
Podemos usar límites para describir el comportamiento infinito de una función en un punto.

Ecuaciones Clave

Definición intuitiva del límite

\(\displaystyle \lim_{x \to a}f(x)=L\)

Dos límites importantes

\(\displaystyle \lim_{x \to a}x=a \qquad \lim_{x \to a}c=c\)

Límites unilaterales

\(\displaystyle \lim_{x \to a^−}f(x)=L \qquad \lim_{x \to a^+}f(x)=L\)

Límites infinitos desde la izquierda

\(\displaystyle \lim_{x \to a^−}f(x)=+∞ \qquad \lim_{x \to a^−} f(x)=−∞\)

Límites infinitos desde la derecha

\(\displaystyle \lim_{x \to a^+}f(x)=+∞ \qquad \lim_{x \to a^+} f(x)=−∞\)

Límites infinitos de dos caras

\(\displaystyle \lim_{x \to a}f(x)=+∞\):\(\displaystyle \lim_{x \to a^−}f(x)=+∞\) y\(\displaystyle \lim_{x \to a^+} f(x)=+∞\)

\(\displaystyle \lim_{x \to a}f(x)=−∞\):\(\displaystyle \lim_{x \to a^−}f(x)=−∞\) y\(\displaystyle \lim_{x \to a^+} f(x)=−∞\)

Glosario

límite infinito: Una función tiene un límite infinito en un punto\(a\) si aumenta o disminuye sin límite a medida que se acerca\(a\)

definición intuitiva del límite: Si todos los valores de la función se\(f(x)\) acercan al número real\(L\) como los valores de\(x(≠a)\) aproximación a,\(f(x)\) se aproxima a L

límite unilateral: Un límite unilateral de una función es un límite tomado de la izquierda o de la derecha

asíntota vertical: Una función tiene una asíntota vertical en\(x=a\) si el límite como se\(x\) acerca\(a\) desde la derecha o la izquierda es infinito

Search

Text Color

Text Size

Margin Size

Font Type

Definición (Intuitivo): Límite

Estrategia de resolución de problemas: evaluación de un límite usando una tabla de valores funcionales

Ejemplo\(\PageIndex{1A}\): Evaluating a Limit Using a Table of Functional Values

Ejemplo\(\PageIndex{1B}\): Evaluating a Limit Using a Table of Functional Values

Ejercicio\(\PageIndex{1}\)

Ejemplo\(\PageIndex{2}\): Evaluating a Limit Using a Graph

Ejercicio\(\PageIndex{2}\)

Dos límites importantes

Ejemplo\(\PageIndex{3}\): Evaluating a Limit That Fails to Exist

Ejercicio\(\PageIndex{3}\)

Definición: Límites unilaterales

Ejemplo\(\PageIndex{4}\): Evaluating One-Sided Limits

Ejercicio\(\PageIndex{4}\)

Relacionar los límites de una cara y de dos caras

Definiciones: Límites infinitos

Ejemplo\(\PageIndex{5}\): Recognizing an Infinite Limit

Ejercicio\(\PageIndex{5}\)

Límites infinitos a partir de enteros positivos

Definición: Asíntotas Verticales

Ejemplo\(\PageIndex{6}\): Finding a Vertical Asymptote

Ejercicio\(\PageIndex{6}\)

Ejemplo\(\PageIndex{7}\): Behavior of a Function at Different Points

Ejercicio\(\PageIndex{7}\)

Ejemplo\(\PageIndex{8}\): Einstein’s Equation