2.1: Una vista previa de Cálculo
- Page ID
- 116798
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Describir el problema tangente y cómo condujo a la idea de un derivado.
- Explique cómo la idea de un límite está involucrada en la solución del problema tangente.
- Reconocer una tangente a una curva en un punto como el límite de las líneas secantes.
- Identificar la velocidad instantánea como el límite de velocidad promedio en un pequeño intervalo de tiempo.
- Describir el problema del área y cómo fue resuelto por la integral.
- Explique cómo la idea de un límite está involucrada en la solución del problema del área.
- Reconocer cómo las ideas de límite, derivada e integral llevaron a los estudios de series infinitas y cálculo multivariable.
A medida que nos embarcamos en nuestro estudio del cálculo, veremos cómo su desarrollo surgió de soluciones comunes a problemas prácticos en áreas como la física de ingeniería, como el problema de los viajes espaciales planteados en el abridor de capítulos. Dos problemas clave llevaron a la formulación inicial del cálculo: (1) el problema de la tangente, o cómo determinar la pendiente de una línea tangente a una curva en un punto; y (2) el problema del área, o cómo determinar el área bajo una curva.
El problema de la tangente y el cálculo diferencial
La tasa de cambio es uno de los conceptos más críticos en el cálculo. Comenzamos nuestra investigación de las tasas de cambio observando las gráficas de las tres líneas\(f(x)=−2x−3,\; g(x)=\dfrac{1}{2}x+1\), y\(h(x)=2\), mostradas en la Figura\(\PageIndex{1}\).
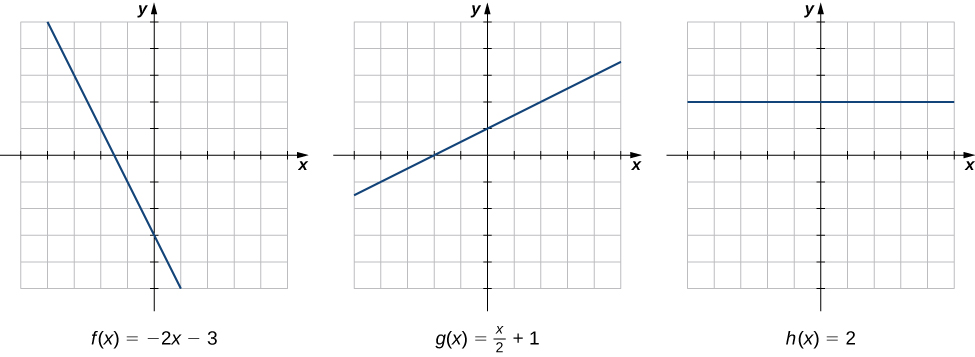
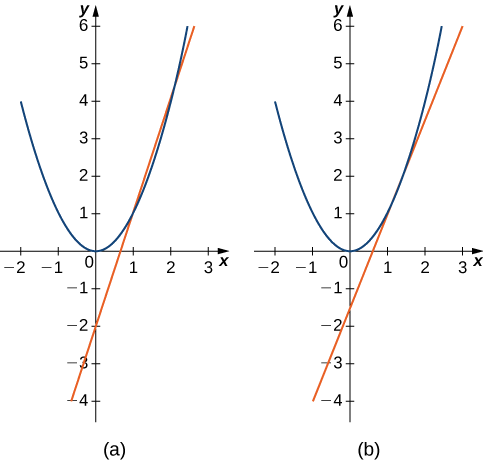
A medida que nos movemos de izquierda a derecha a lo largo de la gráfica de\(f(x)=−2x−3\), vemos que la gráfica disminuye a un ritmo constante. Por cada\(1\) unidad que nos movemos a la derecha a lo largo del\(x\) eje, la\(y\) coordenada -disminuye por\(2\) unidades. Esta tasa de cambio viene determinada por la pendiente (\(−2\)) de la línea. De igual manera, la pendiente de\(1/2\) en la función nos\(g(x)\) dice que por cada cambio en\(x\) de\(1\) unidad hay un cambio correspondiente en\(y\) de\(1/2\) unidad. La función\(h(x)=2\) tiene una pendiente de cero, lo que indica que los valores de la función permanecen constantes. Vemos que la pendiente de cada función lineal indica la tasa de cambio de la función.
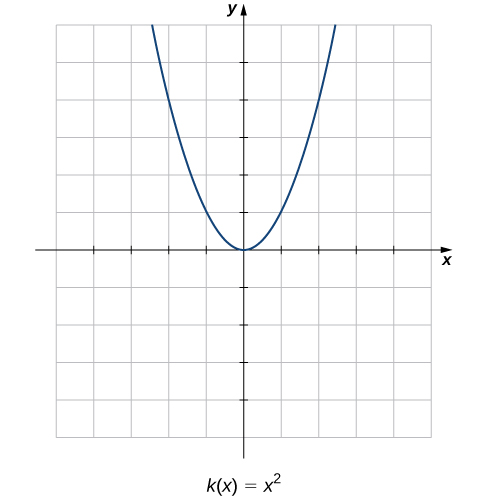
Compara las gráficas de estas tres funciones con la gráfica de\(k(x)=x^2\) (Figura\(\PageIndex{2}\)). La gráfica de\(k(x)=x^2\) comienza desde la izquierda disminuyendo rápidamente, luego comienza a disminuir más lentamente y a nivelarse, y luego finalmente comienza a aumentar—lentamente al principio, seguido de una tasa creciente de aumento a medida que se mueve hacia la derecha. A diferencia de una función lineal, ningún número representa la tasa de cambio para esta función. Naturalmente nos preguntamos: ¿Cómo medimos la tasa de cambio de una función no lineal?
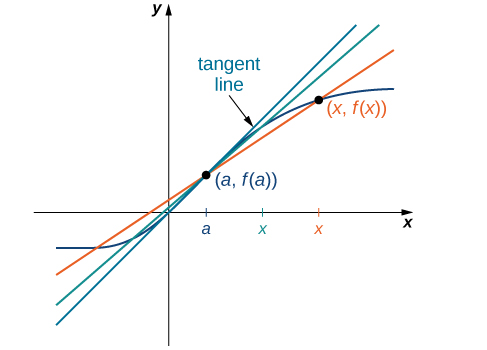
Podemos aproximar la tasa de cambio de una función\(f(x)\) en un punto\((a,f(a))\) de su gráfica tomando otro punto\((x,f(x))\) en la gráfica de\(f(x)\), dibujando una línea a través de los dos puntos, y calculando la pendiente de la línea resultante. Tal línea se llama línea secante. La figura\(\PageIndex{3}\) muestra una línea secante a una función\(f(x)\) en un punto\((a,f(a))\).
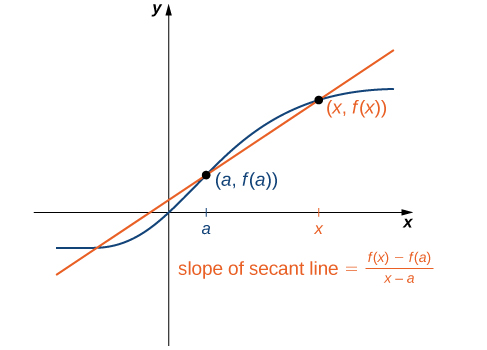
Formalmente definimos una línea secante de la siguiente manera:
La secante a la función\(f(x)\) a través de los puntos\((a,f(a))\) y\((x,f(x))\) es la línea que pasa por estos puntos. Su pendiente viene dada por
\[m_{sec}=\dfrac{f(x)−f(a)}{x−a}. \label{secantslope} \]
La precisión de aproximar la tasa de cambio de la función con una línea secante depende de lo cerca que\(x\) esté de\(a\). Como vemos en la Figura\(\PageIndex{4}\), si\(x\) está más cerca de\(a\), la pendiente de la línea secante es una mejor medida de la tasa de cambio de\(f(x)\) at\(a\).
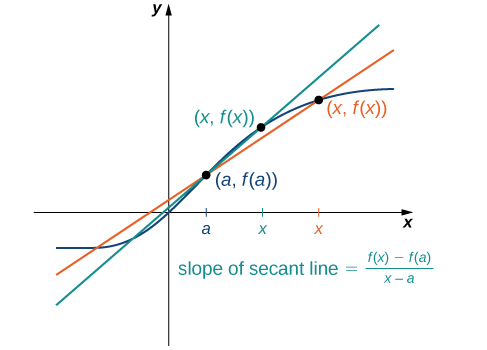
Las propias líneas secantes se acercan a una línea que se llama la tangente a la función\(f(x)\) en\(a\) (Figura\(\PageIndex{5}\)). La pendiente de la línea tangente a la gráfica\(a\) mide la velocidad de cambio de la función a\(a\). Este valor también representa la derivada de la función\(f(x)\) at\(a\), o la tasa de cambio de la función at\(a\). Esta derivada se denota por\(f′(a)\). El cálculo diferencial es el campo del cálculo que se ocupa del estudio de los derivados y sus aplicaciones.
Ejemplo\(\PageIndex{1}\) ilustra cómo encontrar pendientes de líneas secantes. Estas pendientes estiman la pendiente de la línea tangente o, de manera equivalente, la tasa de cambio de la función en el punto en el que se calculan las pendientes.
Estimar la pendiente de la línea tangente (tasa de cambio) a\(f(x)=x^2\) at\(x=1\) encontrando pendientes de líneas secantes a través\((1,1)\) y cada uno de los siguientes puntos en la gráfica de\(f(x)=x^2\).
- \((2,4)\)
- \(\left(\dfrac{3}{2},\dfrac{9}{4}\right)\)
Solución:
Utilice la fórmula para la pendiente de una línea secante (Ecuación\ ref {pendiente secante}).
- \(m_{sec}=\dfrac{4−1}{2−1}=3\)
- \(m_{sec}=\dfrac{\dfrac{9}{4}−1}{\dfrac{3}{2}−1}=\dfrac{5}{2}=2.5\)
El punto en la parte b. está más cerca del punto\((1,1)\), por lo que la pendiente de\(2.5\) está más cerca de la pendiente de la línea tangente. Una buena estimación para la pendiente de la tangente estaría en el rango de\(2\) a\(2.5\) (Figura\(\PageIndex{6}\)).
Estimar la pendiente de la línea tangente (tasa de cambio) a\(f(x)=x^2\) at\(x=1\) mediante la búsqueda de pendientes de líneas secantes a través\((1,1)\) y el punto\((\dfrac{5}{4},\dfrac{25}{16})\) en la gráfica de\(f(x)=x^2\).
- Contestar
-
\(2.25\)
Continuamos nuestra investigación explorando una pregunta relacionada. Teniendo en cuenta que la velocidad puede pensarse como la velocidad de cambio de posición, supongamos que tenemos una función,\(s(t)\), que da la posición de un objeto a lo largo de un eje de coordenadas en un momento dado\(t\). ¿Podemos usar estas mismas ideas para crear una definición razonable de la velocidad instantánea en un momento dado\(t=a?\)? Comenzamos aproximando la velocidad instantánea con una velocidad promedio. En primer lugar, recordemos que la velocidad de un objeto que viaja a una velocidad constante es la relación entre la distancia recorrida y la duración del tiempo que ha recorrido. Definimos la velocidad promedio de un objeto a lo largo de un período de tiempo como el cambio en su posición dividido por la duración del período de tiempo.
Dejar\(s(t)\) ser la posición de un objeto que se mueve a lo largo de un eje de coordenadas en el momento\(t\). La velocidad promedio del objeto a lo largo de un intervalo de tiempo\([a,t]\) donde\(a<t\) (o\([t,a]\) si\(t<a)\) es
\[v_{ave}=\dfrac{s(t)−s(a)}{t−a}. \label{avgvel} \]
A medida\(t\) que se elige más cerca\(a\), la velocidad promedio se vuelve más cercana a la velocidad instantánea. Tenga en cuenta que encontrar la velocidad promedio de una función de posición durante un intervalo de tiempo es esencialmente lo mismo que encontrar la pendiente de una línea secante a una función. Además, para encontrar la pendiente de una línea tangente en un punto\(a\), dejamos que los\(x\) -valores se acerquen\(a\) en la pendiente de la línea secante. De manera similar, para encontrar la velocidad instantánea en el tiempo\(a\), dejamos que los\(t\) -valores se\(a\) aproximen en la velocidad promedio. Este proceso de dejar\(x\) o\(t\) acercarse\(a\) en una expresión se llama tomar un límite. Así, podemos definir la velocidad instantánea de la siguiente manera.
Para una función de posición\(s(t)\), la velocidad instantánea a la vez\(t=a\) es el valor al que se aproximan las velocidades promedio a intervalos de la forma\([a,t]\) y a\([t,a]\) medida que los valores de\(t\) se acercan\(a\), siempre que exista tal valor.
Ejemplo\(\PageIndex{2}\) ilustra este concepto de límites y velocidad media.
Una roca se deja caer desde una altura de 64 pies. Se determina que su altura (en pies) sobre el suelo t segundos después (for\(0≤t≤2\)) viene dada por\(s(t)=−16t^2+64\). Encuentra la velocidad promedio de la roca en cada uno de los intervalos de tiempo dados. Usa esta información para adivinar la velocidad instantánea de la roca en el momento\(t=0.5\).
- [\(0.49,0.5\)]
- [\(0.5,0.51\)]
Solución
Sustituya los datos en Ecuación\ ref {avgvel} para la definición de velocidad promedio.
- \[v_{ave}=\dfrac{s(0.49)−s(0.5)}{0.49−0.5}=−15.84 \nonumber \]
- \[v_{ave}=\dfrac{s(0.51)−s(0.5)}{0.51−0.5}=−16.016 \nonumber \]
La velocidad instantánea está en algún lugar entre −15.84 y −16.16 pies/seg. Una buena conjetura podría ser −16 pies/seg.
Un objeto se mueve a lo largo de un eje de coordenadas de manera que su posición en el tiempo\(t\) viene dada por\(s(t)=t^3\). Estimar su velocidad instantánea en el tiempo\(t=2\) calculando su velocidad promedio a lo largo del intervalo de tiempo [\(2,2.001\)].
- Pista
-
Utilice la ecuación\ ref {avgvel} con\(v_{ave}=\dfrac{s(2.001)−s(2)}{2.001−2}\).
- Contestar
-
12.006001
El problema del área y el cálculo integral
Ahora dirigimos nuestra atención a una pregunta clásica a partir del cálculo. Muchas cantidades en la física, por ejemplo, cantidades de trabajo, pueden interpretarse como el área bajo una curva. Esto nos lleva a hacer la pregunta: ¿Cómo podemos encontrar el área entre la gráfica de una función y el\(x\) eje -sobre un intervalo (Figura\(\PageIndex{7}\))?
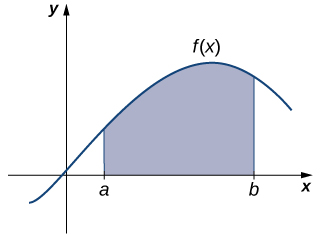
Al igual que en la respuesta a nuestras preguntas anteriores sobre velocidad, primero tratamos de aproximar la solución. Aproximamos el área dividiendo el intervalo\([a,b]\) en intervalos más pequeños en forma de rectángulos. La aproximación del área proviene de sumar las áreas de estos rectángulos (Figura\(\PageIndex{8}\)).
![La gráfica es la misma que la imagen anterior, con una diferencia. En lugar del área completamente sombreada bajo la función curva, el intervalo [a, b] se divide en intervalos más pequeños en forma de rectángulos. Los rectángulos tienen el mismo ancho pequeño. La altura de cada rectángulo es la altura de la función en el punto medio de la base de ese rectángulo específico.](https://math.libretexts.org/@api/deki/files/1846/CNX_Calc_Figure_02_01_007.jpeg)
A medida que los anchos de los rectángulos se hacen más pequeños (se acercan a cero), las sumas de las áreas de los rectángulos se acercan al área entre la gráfica\(f(x)\) y el\(x\) eje sobre el intervalo\([a,b]\). Una vez más, nos encontramos tomando un límite. Límites de este tipo sirven de base para la definición de la integral definida. El cálculo integral es el estudio de las integrales y sus aplicaciones.
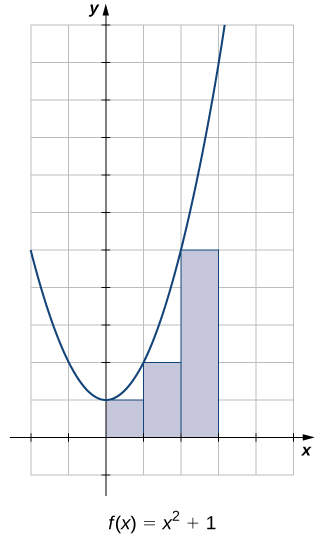
Estimar el área entre el\(x\) eje y la gráfica de\(f(x)=x^2+1\) sobre el intervalo\([0,3]\) utilizando los tres rectángulos que se muestran en la Figura\(\PageIndex{9}\).
Solución
Las áreas de los tres rectángulos son 1 unidad 2, 2 unidad y 5 unidad 2. Usando estos rectángulos, nuestra estimación de área es de 8 unidad 2.
Estimar el área entre el\(x\) eje y la gráfica de\(f(x)=x^2+1\) sobre el intervalo\([0,3]\) utilizando los tres rectángulos que se muestran en la Figura\(\PageIndex{10}\).
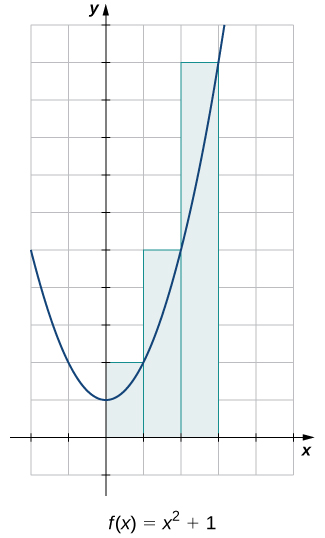
- Pista
-
Use el ejemplo\(\PageIndex{3}\) como guía
- Contestar
-
17\(\mathrm{unit}^2\)
Otros aspectos del cálculo
Hasta el momento, hemos estudiado funciones de una sola variable. Dichas funciones se pueden representar visualmente usando gráficas en dos dimensiones; sin embargo, no hay una buena razón para restringir nuestra investigación a dos dimensiones. Supongamos, por ejemplo, que en lugar de determinar la velocidad de un objeto que se mueve a lo largo de un eje de coordenadas, queremos determinar la velocidad de una roca disparada desde una catapulta en un momento dado, o de un avión que se mueve en tres dimensiones. Podríamos querer graficar funciones de valor real de dos variables o determinar volúmenes de sólidos del tipo que se muestra en la Figura\(\PageIndex{11}\). Estos son solo algunos de los tipos de preguntas que se pueden hacer y responder mediante cálculo multivariable. Informalmente, el cálculo multivariable puede caracterizarse como el estudio del cálculo de funciones de dos o más variables. Sin embargo, antes de explorar estas y otras ideas, primero debemos sentar las bases para el estudio del cálculo en una variable explorando el concepto de límite.
Conceptos clave
- El cálculo diferencial surgió al tratar de resolver el problema de determinar la pendiente de una línea tangente a una curva en un punto. La pendiente de la línea tangente indica la tasa de cambio de la función, también llamada derivada. El cálculo de una derivada requiere encontrar un límite.
- El cálculo integral surgió al tratar de resolver el problema de encontrar el área de una región entre la gráfica de una función y el\(x\) eje -eje. Podemos aproximar el área dividiéndola en rectángulos delgados y sumando las áreas de estos rectángulos. Esta suma conduce al valor de una función llamada integral. La integral también se calcula encontrando un límite y, de hecho, se relaciona con la derivada de una función.
- El cálculo multivariable nos permite resolver problemas en el espacio tridimensional, incluyendo la determinación del movimiento en el espacio y la búsqueda de volúmenes de sólidos.
Ecuaciones Clave
- Pendiente de una Línea Secante
\(m_{sec}=\dfrac{f(x)−f(a)}{x−a}\)
- Velocidad media a lo largo del intervalo [a, t]
\(v_{ave}=\dfrac{s(t)−s(a)}{t−a}\)
Glosario
- velocidad media
- el cambio en la posición de un objeto dividido por la duración de un período de tiempo; la velocidad promedio de un objeto a lo largo de un intervalo de tiempo [\(t,a\)] (si\(t<a\) o [\(a,t\)] si\(t>a\)), con una posición dada por\(s(t)\), es decir\(v_{ave}=\dfrac{s(t)−s(a)}{t−a}\)
- cálculo diferencial
- el campo del cálculo relacionado con el estudio de los derivados y sus aplicaciones
- velocidad instantánea
- La velocidad instantánea de un objeto con una función de posición que viene dada por\(s(t)\) es el valor que las velocidades promedio en intervalos de la forma [\(t,a\)] y [\(a,t\)] se aproximan a medida que los valores de se\(t\) acercan\(a\), siempre que exista tal valor
- cálculo integral
- el estudio de las integrales y sus aplicaciones
- límite
- el proceso de dejar que x o t se acerquen a a en una expresión; el límite de una función\(f(x)\) como\(x\) enfoques\(a\) es el valor que se\(f(x)\) acerca como\(x\) enfoques\(a\)
- cálculo multivariable
- el estudio del cálculo de funciones de dos o más variables
- secante
- Una línea secante a una función\(f(x)\) en\(a\) es una línea a través del punto (\(a,f(a)\)) y otro punto en la función; la pendiente de la línea secante viene dada por\(m_{sec}=\dfrac{f(x)−f(a)}{x−a}\)
- tangente
- Una línea tangente a la gráfica de una función en un punto (\(a,f(a)\)) es la línea que las líneas secantes a través de (\(a,f(a)\)) se acercan a medida que se toman a través de puntos en la función con\(x\) -valores que se acercan\(a\); la pendiente de la línea tangente a una gráfica\(a\) mide la velocidad de cambio de la función en\(a\)


