3.9: Derivadas de funciones exponenciales y logarítmicas

Objetivos de aprendizaje

• Encuentra la derivada de las funciones exponenciales.
• Encuentra la derivada de funciones logarítmicas.
• Utilizar la diferenciación logarítmica para determinar la derivada de una función.

Hasta ahora, hemos aprendido a diferenciar una variedad de funciones, incluyendo funciones trigonométricas, inversas e implícitas. En esta sección, exploramos las derivadas de funciones exponenciales y logarítmicas. Como se discutió en Introducción a las Funciones y Gráficas, las funciones exponenciales juegan un papel importante en el modelado del crecimiento poblacional y la desintegración de materiales radiactivos. Las funciones logarítmicas pueden ayudar a reescalar grandes cantidades y son particularmente útiles para reescribir expresiones complicadas.

Derivada de la Función Exponencial

Así como cuando encontramos las derivadas de otras funciones, podemos encontrar las derivadas de funciones exponenciales y logarítmicas usando fórmulas. A medida que desarrollamos estas fórmulas, necesitamos hacer ciertas suposiciones básicas. Las pruebas que estos supuestos sostienen están más allá del alcance de este curso.

En primer lugar, comenzamos con el supuesto de que la función\(B(x)=b^x,\, b>0,\) está definida para cada número real y es continua. En cursos anteriores, se definieron los valores de las funciones exponenciales para todos los números racionales —comenzando con la definición de\(b^n\), dónde\(n\) es un entero positivo— como producto de\(b\) multiplicar por sí mismo los\(n\) tiempos. Posteriormente, definimos\(b^0=1,b^{−n}=\dfrac{1}{b^n}\), para un entero positivo\(n\), y\(b^{s/t}=(\sqrt[t]{b})^s\) para enteros positivos\(s\) y\(t\). Estas definiciones dejan abierta la cuestión del valor de\(b^r\) dónde\(r\) es un número real arbitrario. Al asumir la continuidad de\(B(x)=b^x,b>0\), podemos interpretar\(b^r\) como\(\displaystyle \lim_{x→r}b^x\) donde los valores de\(x\) como tomamos el límite son racionales. Por ejemplo, podemos ver\(4^π\) como el número satisfactorio

\[4^3<4^π<4^4,\quad 4^{3.1}<4^π<4^{3.2},\quad 4^{3.14}<4^π<4^{3.15}, \nonumber \]

\[4^{3.141}<4^{π}<4^{3.142},\quad 4^{3.1415}<4^{π}<4^{3.1416},\quad …. \nonumber \]

Como vemos en la siguiente tabla,\(4^π≈77.88.\)

\(x\)	\(4^x\)	\(x\)	\(4^x\)
\ (x\)” style="text-align:center; ">\(4^3\)	\ (4^x\)” style="text-align:center; ">64	\ (x\)” style="text-align:center; ">\(4^{3.141593}\)	\ (4^x\)” style="text-align:center; ">77.8802710486
\ (x\)” style="text-align:center; ">\(4^{3.1}\)	\ (4^x\)” style="text-align:center; ">73.5166947198	\ (x\)” style="text-align:center; ">\(4^{3.1416}\)	\ (4^x\)” style="text-align:center; ">77.8810268071
\ (x\)” style="text-align:center; ">\(4^{3.14}\)	\ (4^x\)” style="text-align:center; ">77.7084726013	\ (x\)” style="text-align:center; ">\(4^{3.142}\)	\ (4^x\)” style="text-align:center; ">77.9242251944
\ (x\)” style="text-align:center; ">\(4^{3.141}\)	\ (4^x\)” style="text-align:center; ">77.8162741237	\ (x\)” style="text-align:center; ">\(4^{3.15}\)	\ (4^x\)” style="text-align:center; ">78.7932424541
\ (x\)” style="text-align:center; ">\(4^{3.1415}\)	\ (4^x\)” style="text-align:center; ">77.8702309526	\ (x\)” style="text-align:center; ">\(4^{3.2}\)	\ (4^x\)” style="text-align:center; ">84.4485062895
\ (x\)” style="text-align:center; ">\(4^{3.14159}\)	\ (4^x\)” style="text-align:center; ">77.8799471543	\ (x\)” style="text-align:center; ">\(4^{4}\)	\ (4^x\)” style="text-align:center; ">256

Aproximación a un valor de\(4^π\)

También asumimos que para\(B(x)=b^x,\, b>0\), el valor\(B′(0)\) de la derivada existe. En esta sección, mostramos que al hacer esta suposición adicional, es posible demostrar que la función\(B(x)\) es diferenciable en todas partes.

Hacemos una suposición final: que hay un valor único\(b>0\) para el cual\(B′(0)=1\). Definimos e como este valor único, como lo hicimos en Introducción a las Funciones y Gráficas. La figura\(\PageIndex{1}\) proporciona gráficas de las funciones\(y=2^x, \,y=3^x, \,y=2.7^x,\) y\(y=2.8^x\). Una estimación visual de las pendientes de las líneas tangentes a estas funciones en 0 proporciona evidencia de que el valor de e se encuentra en algún lugar entre 2.7 y 2.8. La función\(E(x)=e^x\) se llama la función exponencial natural. Su inversa,\(L(x)=\log_e x=\ln x\) se llama la función logarítmica natural.

Figura\(\PageIndex{1}\): La gráfica de\(E(x)=e^x\) es entre\(y=2^x\) y\(y=3^x\).

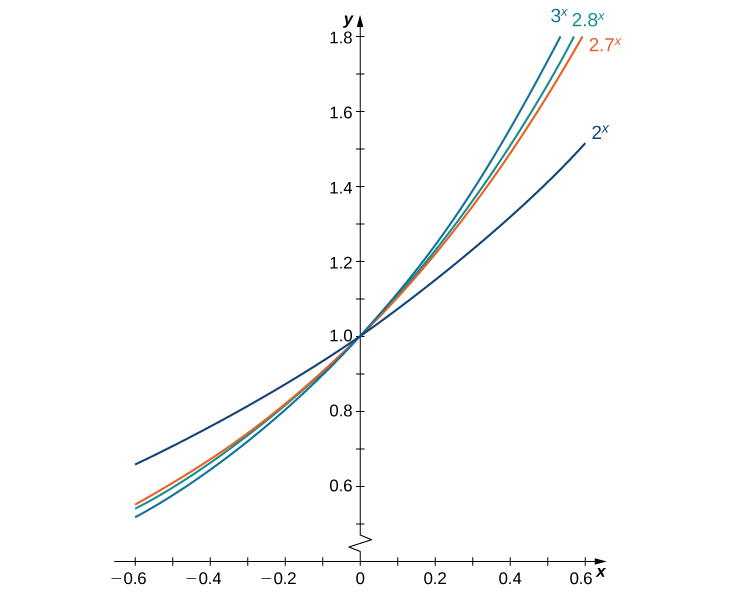
Para una mejor estimación de\(e\), podemos construir una tabla de estimaciones de\(B′(0)\) para funciones de la forma\(B(x)=b^x\). Antes de hacer esto, recordemos que

\[B′(0)=\lim_{x→0}\frac{b^x−b^0}{x−0}=\lim_{x→0}\frac{b^x−1}{x}≈\frac{b^x−1}{x} \nonumber \]

para valores\(x\) muy cercanos a cero. Para nuestras estimaciones, elegimos\(x=0.00001\) y\(x=−0.00001\)

para obtener la estimación

\[\frac{b^{−0.00001}−1}{−0.00001}<B′(0)<\frac{b^{0.00001}−1}{0.00001}. \nonumber \]

Consulte la siguiente tabla.

Tabla: Estimando el valor de\(e\)

\(b\)	\(\frac{b^{−0.00001}−1}{−0.00001}<B′(0)<\frac{b^{0.00001}−1}{0.00001}.\)	\(b\)	\(\frac{b^{−0.00001}−1}{−0.00001}<B′(0)<\frac{b^{0.00001}−1}{0.00001}.\)
\ (b\)” style="text-align:center; ">2	\ (\ frac {b^ {−0.00001} −1} {−0.00001} <B′ (0) <\ frac {b^ {0.00001} −1} {0.00001}.\)” style="text-align:center; ">\(0.693145<B′(0)<0.69315\)	\ (b\)” style="text-align:center; ">2.7183	\ (\ frac {b^ {−0.00001} −1} {−0.00001} <B′ (0) <\ frac {b^ {0.00001} −1} {0.00001}.\)” style="text-align:center; ">\(1.000002<B′(0)<1.000012\)
\ (b\)” style="text-align:center; ">2.7	\ (\ frac {b^ {−0.00001} −1} {−0.00001} <B′ (0) <\ frac {b^ {0.00001} −1} {0.00001}.\)” style="text-align:center; ">\(0.993247<B′(0)<0.993257\)	\ (b\)” style="text-align:center; ">2.719	\ (\ frac {b^ {−0.00001} −1} {−0.00001} <B′ (0) <\ frac {b^ {0.00001} −1} {0.00001}.\)” style="text-align:center; ">\(1.000259<B′(0)<1.000269\)
\ (b\)” style="text-align:center; ">2.71	\ (\ frac {b^ {−0.00001} −1} {−0.00001} <B′ (0) <\ frac {b^ {0.00001} −1} {0.00001}.\)” style="text-align:center; ">\(0.996944<B′(0)<0.996954\)	\ (b\)” style="text-align:center; ">2.72	\ (\ frac {b^ {−0.00001} −1} {−0.00001} <B′ (0) <\ frac {b^ {0.00001} −1} {0.00001}.\)” style="text-align:center; ">\(1.000627<B′(0)<1.000637\)
\ (b\)” style="text-align:center; ">2.718	\ (\ frac {b^ {−0.00001} −1} {−0.00001} <B′ (0) <\ frac {b^ {0.00001} −1} {0.00001}.\)” style="text-align:center; ">\(0.999891<B′(0)<0.999901\)	\ (b\)” style="text-align:center; ">2.8	\ (\ frac {b^ {−0.00001} −1} {−0.00001} <B′ (0) <\ frac {b^ {0.00001} −1} {0.00001}.\)” style="text-align:center; ">\(1.029614<B′(0)<1.029625\)
\ (b\)” style="text-align:center; ">2.7182	\ (\ frac {b^ {−0.00001} −1} {−0.00001} <B′ (0) <\ frac {b^ {0.00001} −1} {0.00001}.\)” style="text-align:center; ">\(0.999965<B′(0)<0.999975\)	\ (b\)” style="text-align:center; ">3	\ (\ frac {b^ {−0.00001} −1} {−0.00001} <B′ (0) <\ frac {b^ {0.00001} −1} {0.00001}.\)” style="text-align:center; ">\(1.098606<B′(0)<1.098618\)

La evidencia de la tabla sugiere que\(2.7182<e<2.7183.\)

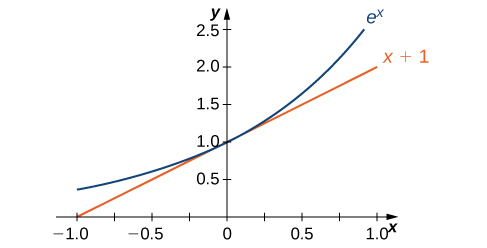
La gráfica de\(E(x)=e^x\) junto con la línea\(y=x+1\) se muestran en la Figura\(\PageIndex{2}\). Esta línea es tangente a la gráfica de\(E(x)=e^x\) at\(x=0\).

Figura\(\PageIndex{2}\): La línea tangente a\(E(x)=e^x\) at\(x=0\) tiene pendiente 1.

Ahora que hemos establecido nuestros supuestos básicos, comenzamos nuestra investigación explorando el derivado de\(B(x)=b^x, \,b>0\). Recordemos que hemos asumido que eso\(B′(0)\) existe. Al aplicar la definición límite a la derivada concluimos que

\[B′(0)=\lim_{h→0}\frac{b^{0+h}−b^0}{h}=\lim_{h→0}\frac{b^h−1}{h} \nonumber \]

Pasando a\(B′(x)\), obtenemos lo siguiente.

\ (\ displaystyle\ begin {align*} B′ (x) &=\ lim_ {h→0}\ frac {b^ {x+h} −b^x} {h} &\ text {Aplica la definición límite de la derivada.}\\ [4pt]
&=\ lim_ {h→0}\ frac {b^xb^h−b^x} {h} & &\ text {Tenga en cuenta que} b^ {x+h} =b^xb^h.\\ [4pt]
&=\ lim_ {h→0}\ frac {b^x (b^h−1)} {h} &\ text {Factor de salida} b^x.\\ [4pt]
&=b^x\ lim_ {h→0}\ frac {b^h−1} {h} & &\ text {Aplicar una propiedad de límites.}\\ [4pt]
&=b^xb′ (0) &\ text {Usar} B′ (0) =\ lim_ {h→0}\ frac {b^ {0+h} −b^0} {h} =\ lim_ {h→0}\ frac {b^h−1} {h}. \ end {alinear*}\)

Vemos que sobre la base de la suposición que\(B(x)=b^x\) es diferenciable en no sólo\(0,B(x)\) es diferenciable en todas partes, sino que su derivada es

\[B′(x)=b^xB′(0).\nonumber \]

Para\(E(x)=e^x, \,E′(0)=1.\) Así, tenemos\(E′(x)=e^x\). (El valor de\(B′(0)\) para una función arbitraria de la forma se\(B(x)=b^x, \,b>0,\) derivará más adelante.)

Derivada de la Función Exponencial Natural

\(E(x)=e^x\)Sea la función exponencial natural. Entonces

\[E′(x)=e^x. \nonumber \]

En general,

\[\frac{d}{dx}\Big(e^{g(x)}\Big)=e^{g(x)}g′(x) \nonumber \]

Ejemplo\(\PageIndex{1}\): Derivative of an Exponential Function

Encuentra la derivada de\(f(x)=e^{\tan(2x)}\).

Solución:

Usando la fórmula derivada y la regla de la cadena,

\[f′(x)=e^{\tan(2x)}\frac{d}{dx}\Big(\tan(2x)\Big)=e^{\tan(2x)}\sec^2(2x)⋅2 \nonumber \]

Ejemplo\(\PageIndex{2}\): Combining Differentiation Rules

Encuentra la derivada de\(y=\dfrac{e^{x^2}}{x}\).

Solución

Utilice la derivada de la función exponencial natural, la regla del cociente y la regla de la cadena.

\ (\ begin {align*} y′&=\ dfrac {(e^ {x^2} y′&=\ dfrac {(e^ {x^2}} &\ text {Aplica la regla del cociente.}\\ [4pt]
&=\ dfrac {e^ {x^2} (2x^2−1)} {x^2} & &\ text {Simplificar.} \ end {alinear*}\)

Ejercicio\(\PageIndex{1}\)

Encuentra la derivada de\(h(x)=xe^{2x}\).

Pista

No olvides usar la regla del producto.

Contestar

\(h′(x)=e^{2x}+2xe^{2x}\)

Ejemplo\(\PageIndex{3}\): Applying the Natural Exponential Function

Una colonia de mosquitos tiene una población inicial de 1000. Después de\(t\) días, la población es dada por\(A(t)=1000e^{0.3t}\). Demostrar que la proporción de la tasa de cambio de la población\(A′(t)\),, a la población,\(A(t)\) es constante.

Solución

Primer hallazgo\(A′(t)\). Al usar la regla de la cadena, tenemos\(A′(t)=300e^{0.3t}.\) Así, la relación de la tasa de cambio de la población a la población viene dada por

\[\frac{A′(t)}{A(t)}=\frac{300e^{0.3t}}{1000e^{0.3t}}=0.3. \nonumber \]

La relación entre la tasa de cambio de la población respecto a la población es la constante 0.3.

Ejercicio\(\PageIndex{2}\)

Si\(A(t)=1000e^{0.3t}\) describe la población de mosquitos después de\(t\) días, como en el ejemplo anterior, ¿cuál es la tasa de cambio de\(A(t)\) después de 4 días?

Pista

Encuentra\(A′(4)\).

Contestar

\(996\)

Derivada de la función logarítmica

Ahora que tenemos la derivada de la función exponencial natural, podemos usar la diferenciación implícita para encontrar la derivada de su inversa, la función logarítmica natural.

Definición: La derivada de la función logarítmica natural

Si\(x>0\) y\(y=\ln x\), entonces

\[\frac{dy}{dx}=\frac{1}{x}. \nonumber \]

De manera más general, deja\(g(x)\) ser una función diferenciable. Para todos los valores de\(x\) para los cuales\(g′(x)>0\), la derivada de\(h(x)=\ln(g(x))\) viene dada por

\[h′(x)=\frac{1}{g(x)}g′(x). \nonumber \]

Prueba

Si\(x>0\) y\(y=\ln x\), entonces\(e^y=x.\) Diferenciar ambos lados de esta ecuación da como resultado la ecuación

\[e^y\frac{dy}{dx}=1. \nonumber \]

Resolviendo\(\dfrac{dy}{dx}\) rendimientos

\[\frac{dy}{dx}=\frac{1}{e^y}. \nonumber \]

Por último, sustituimos\(x=e^y\) para obtener

\[\frac{dy}{dx}=\frac{1}{x}. \nonumber \]

También podemos derivar este resultado aplicando el teorema de la función inversa, de la siguiente manera. Desde\(y=g(x)=\ln x\)

es la inversa de\(f(x)=e^x\), aplicando el teorema de la función inversa tenemos

\[\frac{dy}{dx}=\frac{1}{f′(g(x))}=\frac{1}{e^{\ln x}}=\frac{1}{x}. \nonumber \]

Usar este resultado y aplicar la regla de la cadena a\(h(x)=\ln(g(x))\) los rendimientos

\[h′(x)=\frac{1}{g(x)}g′(x). \label{lnder} \]

□

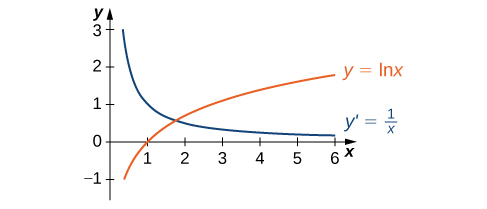
La gráfica de\(y=\ln x\) y su derivada\(\dfrac{dy}{dx}=\dfrac{1}{x}\) se muestran en la Figura\(\PageIndex{3}\).

Figura\(\PageIndex{3}\): La función\(y=\ln x\) está aumentando en\((0,+∞)\). Su derivada\(y'=\frac{1}{x}\) es mayor que cero en\((0,+∞)\)

Ejemplo\(\PageIndex{4}\): Taking a Derivative of a Natural Logarithm

Encuentra la derivada de\(f(x)=\ln(x^3+3x−4)\).

Solución

Usa la ecuación\ ref {lnder} directamente.

\ (\ begin {align*} f′ (x) &=\ dfrac {1} {x^3+3x−4} ⋅ (3x^2+3) &\ text {Usar} g (x) =x^3+3x−4\ texto {en} h′ (x) =\ dfrac {1} {g (x)} g′ (x).\\ [4pt]
&=\ dfrac {3x^2+3} {x^3+3x−4} &\ text {Reescribir.} \ end {alinear*}\)

Ejemplo\(\PageIndex{5}\): Using Properties of Logarithms in a Derivative

Encuentra la derivada de\(f(x)=\ln\left(\dfrac{x^2\sin x}{2x+1}\right)\).

Solución

A primera vista, tomar esta derivada parece bastante complicado. Sin embargo, al usar las propiedades de logaritmos antes de encontrar la derivada, podemos simplificar mucho el problema.

\ (\ begin {align*} f (x) &=\ ln\ left (\ frac {x^2\ sin x} {2x+1}\ derecha) =2\ ln x+\ ln (\ sin x) −\ ln (2x+1) &\ text {Aplicar propiedades de logaritmos.}\\ [4pt]
f′ (x) &=\ dfrac {2} {x} +\ cot x−\ dfrac {2} {2x+1} &\ text {Aplicar regla de suma y} h′ (x) =\ dfrac {1} {g (x)} g′ (x). \ end {alinear*}\)

Ejercicio\(\PageIndex{3}\)

Diferenciar:\(f(x)=\ln(3x+2)^5\).

Pista

Utilizar una propiedad de logaritmos para simplificar antes de tomar la derivada.

Contestar

\(f′(x)=\dfrac{15}{3x+2}\)

Ahora que podemos diferenciar la función logarítmica natural, podemos usar este resultado para encontrar las derivadas de\(y=\log_b x\) y\(y=b^x\) para\(b>0, \,b≠1\).

Derivadas de Funciones Exponenciales y Logarítmicas Generales

Dejar\(b>0,b≠1,\) y dejar\(g(x)\) ser una función diferenciable.

i. Si\(y=\log_b x\), entonces

\[\frac{dy}{dx}=\frac{1}{x\ln b}. \nonumber \]

De manera más general, si\(h(x)=\log_b(g(x))\), entonces para todos los valores de\(x\) para los cuales\(g(x)>0\),

\[h′(x)=\frac{g′(x)}{g(x)\ln b}. \label{genlogder} \]

ii. Si\(y=b^x,\) entonces

\[\frac{dy}{dx}=b^x\ln b. \nonumber \]

De manera más general, si\(h(x)=b^{g(x)},\) entonces

\[h′(x)=b^{g(x)}g'(x)\ln b \label{genexpder} \]

Prueba

Si\(y=\log_b x,\) entonces De\(b^y=x.\) ello se deduce eso\(\ln(b^y)=\ln x\). Por lo tanto\(y\ln b=\ln x\). Resolviendo para\(y\), tenemos\(y=\dfrac{\ln x}{\ln b}\). Diferenciando y teniendo en cuenta que\(\ln b\) es una constante, vemos que

\[\frac{dy}{dx}=\frac{1}{x\ln b}. \nonumber \]

La derivada en la ecuación\ ref {genlogder} ahora sigue de la regla de la cadena.

Si\(y=b^x\). entonces\(\ln y=x\ln b.\) Usando la diferenciación implícita, nuevamente teniendo en cuenta que\(\ln b\) es constante, se deduce de eso\(\dfrac{1}{y}\dfrac{dy}{dx}=\ln b\). Resolviendo\(\dfrac{dy}{dx}\) y sustituyendo\(y=b^x\), vemos que

\[\frac{dy}{dx}=y\ln b=b^x\ln b. \nonumber \]

La derivada más general (Ecuación\ ref {genexpder}) se desprende de la regla de la cadena.

□

Ejemplo\(\PageIndex{6}\): Applying Derivative Formulas

Encuentra la derivada de\(h(x)=\dfrac{3^x}{3^x+2}\).

Solución

Usa la regla del cociente y Note.

\ (\ begin {align*} h′ (x) &=\ dfrac {3^x\ ln 3 (3^x+2) −3^x\ ln 3 (3^x)} {(3^x+2) ^2} &\ text {Aplica la regla del cociente.}\\ [4pt]
&=\ dfrac {23^x\ ln 3} {(3x+2) ^2} & &\ text {Simplificar.} \ end {alinear*}\)

Ejemplo\(\PageIndex{7}\): Finding the Slope of a Tangent Line

Encuentra la pendiente de la línea tangente a la gráfica de\(y=\log_2 (3x+1)\) at\(x=1\).

Solución

Para encontrar la pendiente, debemos evaluar\(\dfrac{dy}{dx}\) en\(x=1\). Usando la ecuación\ ref {genlogder}, vemos que

\[\frac{dy}{dx}=\frac{3}{(3x+1)\ln 2}. \nonumber \]

Al evaluar la derivada en\(x=1\), vemos que la línea tangente tiene pendiente

\[\frac{dy}{dx}\bigg{|}_{x=1}=\frac{3}{4\ln 2}=\frac{3}{\ln 16}. \nonumber \]

Ejercicio\(\PageIndex{4}\)

Encuentra el talud para la línea tangente\(y=3^x\) a\(x=2.\)

Pista

Evaluar la derivada en\(x=2.\)

Contestar

\(9\ln(3)\)

La diferenciación logarítmica

En este punto, podemos tomar derivadas de funciones de la forma\(y=(g(x))^n\) para ciertos valores de\(n\), así como funciones de la forma\(y=b^{g(x)}\), dónde\(b>0\) y\(b≠1\). Desafortunadamente, todavía no conocemos las derivadas de funciones como\(y=x^x\) o\(y=x^π\). Estas funciones requieren de una técnica llamada diferenciación logarítmica, que nos permite diferenciar cualquier función de la forma\(h(x)=g(x)^{f(x)}\). También se puede utilizar para convertir un problema de diferenciación muy complejo en uno más simple, como encontrar la derivada de\(y=\dfrac{x\sqrt{2x+1}}{e^x\sin^3 x}\). Describimos esta técnica en la siguiente estrategia de resolución de problemas.

Estrategia de resolución de problemas: uso de diferenciación logarítmica

1. Para diferenciar\(y=h(x)\) usando diferenciación logarítmica, tomar el logaritmo natural de ambos lados de la ecuación para obtener\(\ln y=\ln(h(x)).\)
2. Usa propiedades de logaritmos para\(\ln(h(x))\) expandirte tanto como sea posible.
3. Diferenciar ambos lados de la ecuación. A la izquierda tendremos\(\dfrac{1}{y}\dfrac{dy}{dx}\).
4. Multiplique ambos lados de la ecuación por\(y\) para resolver para\(\dfrac{dy}{dx}\).
5. Reemplazar\(y\) por\(h(x)\).

Ejemplo\(\PageIndex{8}\): Using Logarithmic Differentiation

Encuentra la derivada de\(y=(2x^4+1)^{\tan x}\).

Solución

Utilice la diferenciación logarítmica para encontrar esta derivada.

\ (\ begin {align*}\ ln y&=\ ln (2x^4+1) ^ {\ tan x} &\ text {Paso 1. Toma el logaritmo natural de ambos lados.}\\ [4pt]
\ ln y&=\ tan x\ ln (2x^4+1) &\ text {Paso 2. Expandir usando propiedades de logaritmos.}\\ [4pt]
\ dfrac {1} {y}\ dfrac {dy} {dx} &=\ sec^2 x\ ln (2x^4+1) +\ dfrac {8x^3} {2x^4+1} ⋅\ tan x & &\ text {Paso 3. Diferenciar ambos lados. Usa la regla del producto a la derecha.}\\ [4pt]
\ dfrac {dy} {dx} &=y⋅ (\ seg^2 x\ ln (2x^4+1) +\ dfrac {8x^3} {2x^4+1} ⋅\ tan x) &\ text {Paso 4. Multiplica por} y\ texto {en ambos lados.}\\ [4pt]
\ dfrac {dy} {dx} & =( 2x^4+1) ^ {\ tan x} (\ seg^2 x\ ln (2x^4+1) +\ dfrac {8x^3} {2x^4+1} ⋅\ tan x) &\ text {Paso 5. Sustituir} y= (2x^4+1) ^ {\ tan x}. \ end {alinear*}\)

Ejemplo\(\PageIndex{9}\): Extending the Power Rule

Encuentra la derivada de\(y=\dfrac{x\sqrt{2x+1}}{e^x\sin^3 x}\).

Solución

Este problema realmente hace uso de las propiedades de los logaritmos y las reglas de diferenciación dadas en este capítulo.

\(\ln y=\ln\dfrac{x\sqrt{2x+1}}{e^x\sin^3 x}\)	Paso 1. Toma el logaritmo natural de ambos lados.
\(\ln y=\ln x+\frac{1}{2}\ln(2x+1)−x\ln e−3\ln \sin x\)	Paso 2. Expandir usando propiedades de logaritmos.
\(\dfrac{1}{y}\dfrac{dy}{dx}=\dfrac{1}{x}+\dfrac{1}{2x+1}−1−3\dfrac{\cos x}{\sin x}\)	Paso 3. Diferenciar ambos lados.
\(\dfrac{dy}{dx}=y\left(\dfrac{1}{x}+\dfrac{1}{2x+1}−1−3\cot x\right)\)	Paso 4. Multiplicar por\(y\) en ambos lados.
\(\dfrac{dy}{dx}=\dfrac{x\sqrt{2x+1}}{e^x\sin^3 x}\left(\dfrac{1}{x}+\dfrac{1}{2x+1}−1−3\cot x\right)\)	Paso 5. Sustituto\(y=\dfrac{x\sqrt{2x+1}}{e^x\sin^3 x}.\)

Ejercicio\(\PageIndex{5}\)

Utilice la diferenciación logarítmica para encontrar la derivada de\(y=x^x\).

Pista

Siga la estrategia de resolución de problemas.

Contestar

Solución:\(\dfrac{dy}{dx}=x^x(1+\ln x)\)

Ejercicio\(\PageIndex{6}\)

Encuentra la derivada de\(y=(\tan x)^π\).

Pista

Usa la regla de potencia (ya que el exponente\(\pi\) es una constante) y la regla de cadena.

Contestar

\(y′=π(\tan x)^{π−1}\sec^2 x\)

Conceptos clave

• Sobre la base del supuesto de que la función exponencial\(y=b^x, \,b>0\) es continua en todas partes y diferenciable en\(0\), esta función es diferenciable en todas partes y hay una fórmula para su derivada.
• Podemos usar una fórmula para encontrar la derivada de\(y=\ln x\), y la relación nos\(\log_b x=\dfrac{\ln x}{\ln b}\) permite extender nuestras fórmulas de diferenciación para incluir logaritmos con bases arbitrarias.
• La diferenciación logarítmica nos permite diferenciar funciones de la forma\(y=g(x)^{f(x)}\) o funciones muy complejas tomando el logaritmo natural de ambos lados y explotando las propiedades de los logaritmos antes de diferenciarlos.

Ecuaciones Clave

• Derivada de la función exponencial natural

\(\dfrac{d}{dx}\Big(e^{g(x)}\Big)=e^{g(x)}g′(x)\)

• Derivada de la función logarítmica natural

\(\dfrac{d}{dx}\Big(\ln g(x)\Big)=\dfrac{1}{g(x)}g′(x)\)

• Derivada de la función exponencial general

\(\dfrac{d}{dx}\Big(b^{g(x)}\Big)=b^{g(x)}g′(x)\ln b\)

• Derivada de la función logarítmica general

\(\dfrac{d}{dx}\Big(\log_b g(x)\Big)=\dfrac{g′(x)}{g(x)\ln b}\)

Glosario

diferenciación logarítmica

es una técnica que nos permite diferenciar una función tomando primero el logaritmo natural de ambos lados de una ecuación, aplicando propiedades de logaritmos para simplificar la ecuación, y diferenciando implícitamente