3.8: Diferenciación implícita
- Page ID
- 116647
- Encontrar la derivada de una función complicada mediante el uso de diferenciación implícita.
- Utilice la diferenciación implícita para determinar la ecuación de una línea tangente.
Ya hemos estudiado cómo encontrar ecuaciones de líneas tangentes a funciones y la tasa de cambio de una función en un punto específico. En todos estos casos tuvimos la ecuación explícita para la función y las diferenciamos explícitamente. Supongamos en cambio que queremos determinar la ecuación de una línea tangente a una curva arbitraria o la tasa de cambio de una curva arbitraria en un punto. En esta sección, resolvemos estos problemas encontrando las derivadas de funciones que definen\(y\) implícitamente en términos de\(x\).
Diferenciación implícita
En la mayoría de las discusiones de matemáticas, si la variable dependiente\(y\) es una función de la variable independiente\(x\), expresamos y en términos de\(x\). Si este es el caso, decimos que\(y\) es una función explícita de\(x\). Por ejemplo, cuando escribimos la ecuación\(y=x^2+1\), estamos definiendo y explícitamente en términos de\(x\). Por otro lado, si la relación entre la función\(y\) y la variable\(x\) se expresa mediante una ecuación donde no\(y\) se expresa enteramente en términos de\(x\), decimos que la ecuación define\(y\) implícitamente en términos de\(x\). Por ejemplo, la ecuación\(y−x^2=1\) define la función\(y=x^2+1\) implícitamente.
La diferenciación implícita nos permite encontrar pendientes de tangentes a curvas que claramente no son funciones (fallan en la prueba de línea vertical). Estamos usando la idea de que porciones de\(y\) son funciones que satisfacen la ecuación dada, pero que y no es en realidad una función de\(x\).
En general, una ecuación define una función implícitamente si la función satisface esa ecuación. Una ecuación puede definir muchas funciones diferentes implícitamente. Por ejemplo, las funciones
\[y=\sqrt{25−x^2}\nonumber \]
y
\[y=\begin{cases}\sqrt{25−x^2}, & \text{if }−5≤x<0\\ −\sqrt{25−x^2}, & \text{if }0≤x≤5\end{cases}\nonumber \]
que se ilustran en la Figura\(\PageIndex{1}\), son solo dos de las muchas funciones definidas implícitamente por la ecuación\(x^2+y^2=25\).
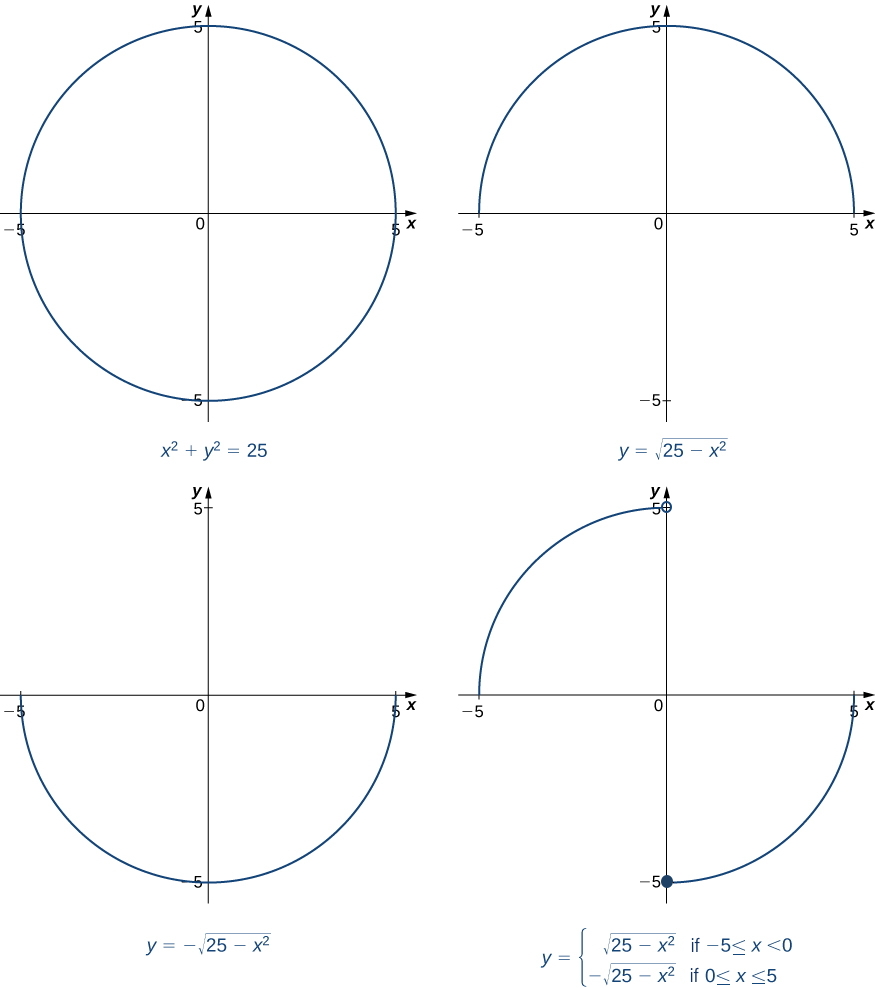
Si queremos encontrar la pendiente de la línea tangente a la gráfica de\(x^2+y^2=25\) en el punto\((3,4)\), podríamos evaluar la derivada de la función\(y=\sqrt{25−x^2}\) at\(x=3\). Por otro lado, si queremos la pendiente de la línea tangente en el punto\((3,−4)\), podríamos usar la derivada de\(y=−\sqrt{25−x^2}\). Sin embargo, no siempre es fácil de resolver para una función definida implícitamente por una ecuación. Afortunadamente, la técnica de diferenciación implícita nos permite encontrar la derivada de una función implícitamente definida sin resolver nunca para la función explícitamente. El proceso de búsqueda\(\dfrac{dy}{dx}\) mediante diferenciación implícita se describe en la siguiente estrategia de resolución de problemas.
Para realizar la diferenciación implícita en una ecuación que define una función\(y\) implícitamente en términos de una variable\(x\), utilice los siguientes pasos:
- Toma la derivada de ambos lados de la ecuación. Tenga en cuenta que\(y\) es una función de\(x\). En consecuencia, mientras\[\dfrac{d}{dx}(\sin x)=\cos x\nonumber \] y\[\dfrac{d}{dx}(\sin y)=\cos y\cdot\dfrac{dy}{dx}\nonumber \] porque debemos usar la regla de la cadena para diferenciar\(\sin y\) con respecto a\(x\).
- Reescribe la ecuación para que todos los términos que contengan\(dy/dx\) estén a la izquierda y todos los términos que no contengan\(dy/dx\) estén a la derecha.
- Factor hacia fuera\(dy/dx\) a la izquierda.
- Resuelve\(dy/dx\) dividiendo ambos lados de la ecuación por una expresión algebraica apropiada.
Suponiendo que\(y\) se define implícitamente por la ecuación\(x^2+y^2=25\), encuentra\(\dfrac{dy}{dx}\).
Solución
Siga los pasos de la estrategia de resolución de problemas.
| \(\dfrac{d}{dx}(x^2+y^2)=\dfrac{d}{dx}(25)\) | Paso 1. Diferenciar ambos lados de la ecuación. |
| \(\dfrac{d}{dx}(x^2)+\dfrac{d}{dx}(y^2)=0\) | Paso 1.1. Usa la regla de suma de la izquierda. A la derecha\(\dfrac{d}{dx}(25)=0\). |
| \(2x+2y\dfrac{dy}{dx}=0\) | Paso 1.2. Toma los derivados, así\(\dfrac{d}{dx}(x^2)=2x\) y\(\dfrac{d}{dx}(y^2)=2y\dfrac{dy}{dx}\). |
| \(2y\dfrac{dy}{dx}=−2x\) | Paso 2. Mantener los términos con\(\dfrac{dy}{dx}\) a la izquierda. Mueva los términos restantes a la derecha. |
| \(\dfrac{dy}{dx}=−\dfrac{x}{y}\) | Paso 4. Dividir ambos lados de la ecuación por\(2y\). (El paso 3 no aplica en este caso.) |
Análisis
Tenga en cuenta que la expresión resultante para\(\dfrac{dy}{dx}\) es en términos tanto de la variable independiente como\(x\) de la variable dependiente\(y\). Si bien en algunos casos puede ser posible expresarse\(\dfrac{dy}{dx}\) en términos de\(x\) solo, generalmente no es posible hacerlo.
Suponiendo que\(y\) se define implícitamente por la ecuación\(x^3\sin y+y=4x+3\), encuentra\(\dfrac{dy}{dx}\).
Solución
| \(\dfrac{d}{dx}(x^3\sin y+y)=\dfrac{d}{dx}(4x+3)\) | Paso 1: Diferenciar ambos lados de la ecuación. |
| \(\dfrac{d}{dx}(x^3\sin y)+\dfrac{d}{dx}(y)=4\) | Paso 1.1: Aplicar la regla de suma a la izquierda. A la derecha,\(\dfrac{d}{dx}(4x+3)=4\). |
| \(\left(\dfrac{d}{dx}(x^3)⋅\sin y+\dfrac{d}{dx}(\sin y)⋅x^3\right)+\dfrac{dy}{dx}=4\) | Paso 1.2: Usa la regla del producto para encontrar\(\dfrac{d}{dx}(x^3\sin y)\). Observe eso\(\dfrac{d}{dx}(y)=\dfrac{dy}{dx}\). |
| \(3x^2\sin y+(\cos y\dfrac{dy}{dx})⋅x^3+\dfrac{dy}{dx}=4\) | Paso 1.3: Sabemos\(\dfrac{d}{dx}(x^3)=3x^2\). Utilice la regla de la cadena para obtener\(\dfrac{d}{dx}(\sin y)=\cos y\dfrac{dy}{dx}\). |
| \(x^3\cos y\dfrac{dy}{dx}+\dfrac{dy}{dx}=4−3x^2\sin y\) | Paso 2: Mantener todos los términos que contengan\(\dfrac{dy}{dx}\) a la izquierda. Mueva todos los demás términos a la derecha. |
| \(\dfrac{dy}{dx}(x^3\cos y+1)=4−3x^2\sin y\) | Paso 3: Facturar hacia fuera a\(\dfrac{dy}{dx}\) la izquierda. |
| \(\dfrac{dy}{dx}=\dfrac{4−3x^2\sin y}{x^3\cos y+1}\) | Paso 4: Resuelve para\(\dfrac{dy}{dx}\) dividiendo ambos lados de la ecuación por\(x^3\cos y+1\). |
Encuentra\(\dfrac{d^2y}{dx^2}\) si\(x^2+y^2=25\).
Solución
En Ejemplo\(\PageIndex{1}\), lo demostramos\(\dfrac{dy}{dx}=−\dfrac{x}{y}\). Podemos tomar la derivada de ambos lados de esta ecuación para encontrar\(\dfrac{d^2y}{dx^2}\).
\ (\ begin {align*}\ dfrac {d^2y} {dx^2} &=\ dfrac {d} {dy}\ left (−\ dfrac {x} {y}\ derecha) &\ text {Diferenciar ambos lados de}\ dfrac {dy} {dx} =−\ dfrac {x} {y}.\\ [4pt]
&=−\ dfrac {\ left (1y−x\ dfrac {dy} {dx}\ derecha)} {y^2} & &\ text {Usa la regla del cociente para encontrar}\ dfrac {d} {dy}\ left (−\ dfrac {x} {y} \ derecha).\\ [4pt]
&=\ dfrac {−y+x\ dfrac {dy} {dx}} {y^2} & &\ text {Simplificar.}\\ [4pt]
&=\ dfrac {−y+x\ left (−\ dfrac {x} {y}\ derecha)} {y^2} &\ text {Sustituir}\ dfrac {dy} {dx} =−\ dfrac {x} {y}.\\ [4pt]
&=\ dfrac {−y^2−x^2} {y^3} & &\ text {Simplificar.} \ end {alinear*}\)
En este punto hemos encontrado una expresión para\(\dfrac{d^2y}{dx^2}\). Si elegimos, podemos simplificar aún más la expresión recordando eso\(x^2+y^2=25\) y haciendo esta sustitución en el numerador para obtener\(\dfrac{d^2y}{dx^2}=−\dfrac{25}{y^3}\).
Encontrar\(\dfrac{dy}{dx}\) para\(y\) definido implícitamente por la ecuación\(4x^5+\tan y=y^2+5x\).
- Insinuación
-
Siga la estrategia de resolución de problemas, recordando aplicar la regla de la cadena para diferenciar\(\tan y\) y\(y^2\).
- Contestar
-
\[\dfrac{dy}{dx}=\dfrac{5−20x^4}{\sec^2y−2y} \nonumber \]
Encontrar líneas tangentes implícitamente
Ahora que hemos visto la técnica de diferenciación implícita, podemos aplicarla al problema de encontrar ecuaciones de líneas tangentes a curvas descritas por ecuaciones.
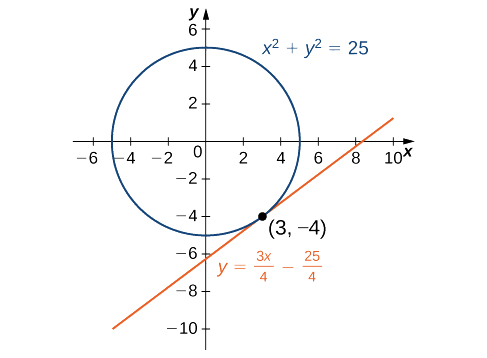
Encuentra la ecuación de la línea tangente a la curva\(x^2+y^2=25\) en el punto\((3,−4)\).
Solución
Aunque podríamos encontrar esta ecuación sin usar diferenciación implícita, usar ese método la hace mucho más fácil. En Ejemplo\(\PageIndex{1}\), encontramos\(\dfrac{dy}{dx}=−\dfrac{x}{y}\).
La pendiente de la línea tangente se encuentra sustituyendo\((3,−4)\) en esta expresión. En consecuencia, la pendiente de la línea tangente es\(\dfrac{dy}{dx}\Big|_{(3,−4)}=−\dfrac{3}{−4}=\dfrac{3}{4}\).
Usando el punto\((3,−4)\) y la pendiente\(\dfrac{3}{4}\) en la ecuación punto-pendiente de la línea, obtenemos la ecuación\(y=\dfrac{3}{4}x−\dfrac{25}{4}\) (Figura\(\PageIndex{2}\)).
Encuentra la ecuación de la línea tangente a la gráfica de\(y^3+x^3−3xy=0\) en el punto\(\left(\frac{3}{2},\frac{3}{2}\right)\) (Figura\(\PageIndex{3}\)). Esta curva se conoce como el folium (u hoja) de Descartes.
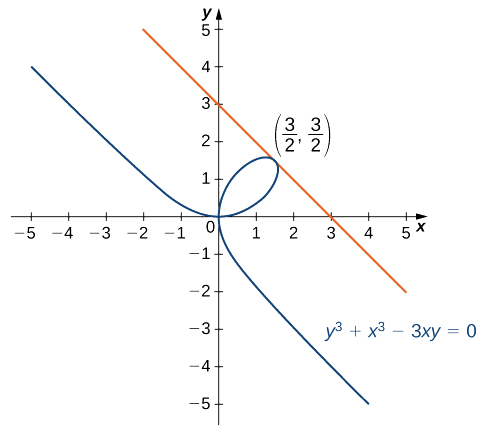
Solución
Comience por encontrar\(\dfrac{dy}{dx}\).
\(\dfrac{d}{dx}\big(y^3+x^3−3xy\big)=\dfrac{d}{dx}\big(0\big)\)
\(3y^2\dfrac{dy}{dx}+3x^2−\left(3y+3x\dfrac{dy}{dx}\right)=0\)
\(3y^2\dfrac{dy}{dx}+3x^2−3y-3x\dfrac{dy}{dx}=0\)
\(\left(3y^2-3x\right)\dfrac{dy}{dx}=3y-3x^2\)
\(\dfrac{dy}{dx}=\dfrac{3y−3x^2}{3y^2−3x}\).
A continuación, sustituya\(\left(\frac{3}{2},\frac{3}{2}\right)\)\(\dfrac{dy}{dx}=\dfrac{3y−3x^2}{3y^2−3x}\) por para encontrar la pendiente de la línea tangente:
\(\dfrac{dy}{dx}\Bigg|_{\left(\frac{3}{2},\frac{3}{2}\right)}=−1\).
Finalmente, sustituya en la ecuación punto-pendiente de la línea para obtener
\(y=−x+3\).
En un sencillo videojuego, un cohete viaja en una órbita elíptica cuya trayectoria es descrita por la ecuación\(4x^2+25y^2=100\). El cohete puede disparar misiles a lo largo de líneas tangentes a su trayectoria. El objeto del juego es destruir un asteroide entrante que viaja a lo largo del\(x\) eje positivo hacia\((0,0)\). Si el cohete dispara un misil cuando se encuentra en\(\left(3,\frac{8}{5}\right)\), ¿dónde cruzará el\(x\) eje -eje?
Solución
Para resolver este problema, debemos determinar dónde está la línea tangente a la gráfica de
\(4x^2+25y^2=100\)en\(\left(3,\frac{8}{5}\right)\) intersecta el\(x\) eje. Comience por encontrar\(\dfrac{dy}{dx}\) implícitamente.
Diferenciando, tenemos
\(8x+50y\dfrac{dy}{dx}=0.\)
Resolviendo para\(\dfrac{dy}{dx}\),
tenemos
\(\dfrac{dy}{dx}=−\dfrac{4x}{25y}\).
La pendiente de la línea tangente es\(\dfrac{dy}{dx}\Bigg|_{\left(3,\frac{8}{5}\right)}=−\dfrac{3}{10}\). La ecuación de la línea tangente es\(y=−\dfrac{3}{10}x+\dfrac{5}{2}\). Para determinar dónde se cruza la línea con el\(x\) eje -eje, resuelva\(0=−\dfrac{3}{10}x+\dfrac{5}{2}\). La solución es\(x=\dfrac{25}{3}\). El misil cruza el\(x\) eje -en el punto\(\left(\frac{25}{3},0\right)\).
Encuentra la ecuación de la línea tangente a la hipérbola\(x^2−y^2=16\) en el punto\((5,3)\).
- Insinuación
-
\(\dfrac{dy}{dx}=\dfrac{x}{y}\)
- Contestar
-
\(y=\dfrac{5}{3}x−\dfrac{16}{3}\)
Conceptos clave
- Utilizamos la diferenciación implícita para encontrar derivadas de funciones definidas implícitamente (funciones definidas por ecuaciones).
- Mediante el uso de diferenciación implícita, podemos encontrar la ecuación de una línea tangente a la gráfica de una curva.
Glosario
- diferenciación implícita
- es una técnica\(\dfrac{dy}{dx}\) para calcular una función definida por una ecuación, lograda diferenciando ambos lados de la ecuación (recordando tratar la variable\(y\) como una función) y resolviendo para\(\dfrac{dy}{dx}\)