4.9: Método de Newton

Última actualización
Guardar como PDF

Page ID: 116404

Edwin “Jed” Herman & Gilbert Strang
OpenStax

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Objetivos de aprendizaje

Describir los pasos del método de Newton.
Explicar lo que significa un proceso iterativo.
Reconocer cuando el método de Newton no funciona.
Aplicar procesos iterativos a diversas situaciones.

En muchas áreas de las matemáticas puras y aplicadas, nos interesa encontrar soluciones a una ecuación de la forma\(f(x)=0.\) Para la mayoría de las funciones, sin embargo, es difícil —si no imposible— calcular sus ceros explícitamente. En esta sección, echamos un vistazo a una técnica que proporciona una manera muy eficiente de aproximar los ceros de funciones. Esta técnica hace uso de aproximaciones de líneas tangentes y está detrás del método utilizado a menudo por calculadoras y computadoras para encontrar ceros.

Describiendo el método de Newton

Considera la tarea de encontrar las soluciones de\(f(x)=0.\) Si\(f\) es el polinomio de primer grado\(f(x)=ax+b\), entonces la solución de\(f(x)=0\) viene dada por la fórmula\(x=−\frac{b}{a}\). Si\(f\) es el polinomio de segundo grado\(f(x)=ax^2+bx+c\), las soluciones de se\(f(x)=0\) pueden encontrar usando la fórmula cuadrática. Sin embargo, para polinomios de grado 3 o más, encontrar raíces de\(f\) se vuelve más complicado. Aunque existen fórmulas para polinomios de tercer y cuarto grado, son bastante complicadas. También, si f es un polinomio de grado 5 o superior, se sabe que no existen tales fórmulas. Por ejemplo, considere la función

\[f(x)=x^5+8x^4+4x^3−2x−7.\nonumber \]

No existe ninguna fórmula que nos permita encontrar las soluciones de Dificultades\(f(x)=0.\) similares existen para funciones no polinómicas. Por ejemplo, considere la tarea de encontrar soluciones de\(\tan(x)−x=0.\) No existe una fórmula simple para las soluciones de esta ecuación. En casos como estos, podemos usar el método de Newton para aproximar las raíces.

El método de Newton hace uso de la siguiente idea para aproximar las soluciones de\(f(x)=0.\) Al esbozar una gráfica de\(f\), podemos estimar una raíz de\(f(x)=0\). Llamemos a esta estimación\(x_0\). Luego dibujamos la línea tangente a\(f\) at\(x_0\). Si\(f′(x_0)≠0\), esta línea tangente cruza el\(x\) eje -en algún punto\((x_1,0)\). Ahora deja\(x_1\) ser la siguiente aproximación a la raíz real. Por lo general,\(x_1\) está más cerca\(x_0\) que de una raíz real. A continuación dibujamos la línea tangente a\(f\) at\(x_1\). Si\(f′(x_1)≠0\), esta línea tangente también cruza el\(x\) eje -eje, produciendo otra aproximación,\(x_2\). Continuamos de esta manera, derivando una lista de aproximaciones:\(x_0,\, x_1,\, x_2,\, ….\) Normalmente, los números se acercan\(x_0,\, x_1,\, x_2,\, …\) rápidamente a una raíz real\(x^*\), como se muestra en la siguiente figura.

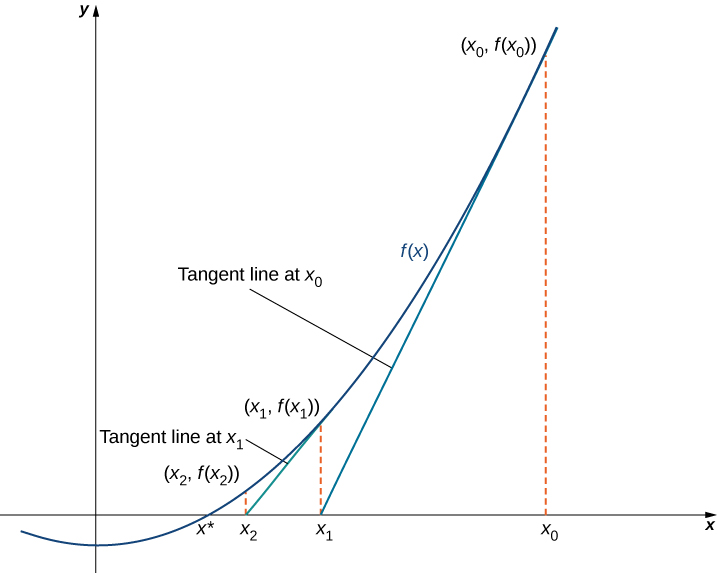
Esta función f (x) se dibuja con puntos (x0, f (x0)), (x1, f (x1)) y (x2, f (x2)) marcados en la función. De (x0, f (x0)), se dibuja una línea tangente, y golpea el eje x en x1. De (x0, f (x0)), se dibuja una línea tangente, y golpea el eje x en x2. Si se dibujara una línea tangente de (x2, f (x2)), parece que se acercaría mucho a x*, que es la raíz real. Cada línea tangente dibujada en este orden parece acercarse cada vez más a x*. — Figura:Las\(\PageIndex{1}\) aproximaciones se acercan\(x_0,\, x_1,\, x_2,\, … \) a la raíz real.\(x^*\) Las aproximaciones se derivan observando líneas tangentes a la gráfica de\(f\).

Ahora veamos cómo calcular las aproximaciones\(x_0,\, x_1,\, x_2,\, ….\) Si\(x_0\) es nuestra primera aproximación, la aproximación\(x_1\) se define dejando\((x_1,0)\) ser la\(x\) -intercepción de la línea tangente a\(f\) at\(x_0\). La ecuación de esta línea tangente viene dada por

\[y=f(x_0)+f′(x_0)(x−x_0). \nonumber \]

Por lo tanto,\(x_1\) debe satisfacer

\[f(x_0)+f′(x_0)(x_1−x_0)=0.\nonumber \]

Resolviendo esta ecuación para\(x_1\), concluimos que

\[x_1=x_0−\frac{f(x_0)}{f'(x_0)}.\nonumber \]

Del mismo modo, el punto\((x_2,0)\) es la\(x\) intersección de la línea tangente a\(f\) at\(x_1\). Por lo tanto,\(x_2\) satisface la ecuación

\[x_2=x_1−\frac{f(x_1)}{f'(x_1)}.\nonumber \]

En general, para\(n>0,x_n\) satisface

\[x_n=x_{n−1}−\frac{f(x_{n−1})}{f'(x_{n−1})}.\label{Newton} \]

A continuación vemos cómo hacer uso de esta técnica para aproximar la raíz del polinomio\(f(x)=x^3−3x+1.\)

Ejemplo\(\PageIndex{1}\): Finding a Root of a Polynomial

Utilice el método de Newton para aproximar una raíz de\(f(x)=x^3−3x+1\) en el intervalo\([1,2]\). Dejar\(x_0=2\) y encontrar\(x_1,\, x_2, \,x_3, \,x_4,\) y\(x_5\).

Solución

De la Figura\(\PageIndex{2}\), vemos que\(f\) tiene una raíz sobre el intervalo\([1,2]\). Por lo tanto,\(x_0=2\) parece una primera aproximación razonable. Para encontrar la siguiente aproximación, usamos la Ecuación\ ref {Newton}. Ya que\(f(x)=x^3−3x+1\), el derivado es\(f′(x)=3x^2−3\). Usando la ecuación\ ref {Newton} con\(n=1\) (y una calculadora que muestra\(10\) dígitos), obtenemos

\[x_1=x_0−\frac{f(x_0)}{f'(x_0)}=2−\frac{f(2)}{f'(2)}=2−\frac{3}{9}≈1.666666667.\nonumber \]

Para encontrar la siguiente aproximación,\(x_2\), utilizamos la Ecuación\ ref {Newton} con\(n=2\) y el valor de\(x_1\) almacenado en la calculadora. Encontramos que

\[x_2=x_1-\frac{f(x_1)}{f'(x_1)}≈1.548611111.\nonumber \]

Continuando de esta manera, obtenemos los siguientes resultados:

\(x_1≈1.666666667\)
\(x_2≈1.548611111\)
\(x_3≈1.532390162\)
\(x_4≈1.532088989\)
\(x_5≈1.532088886\)
\(x_6≈1.532088886.\)

Observamos que obtuvimos el mismo valor para\(x_5\) y\(x_6\). Por lo tanto, cualquier aplicación posterior del método de Newton probablemente dará el mismo valor para\(x_n\).

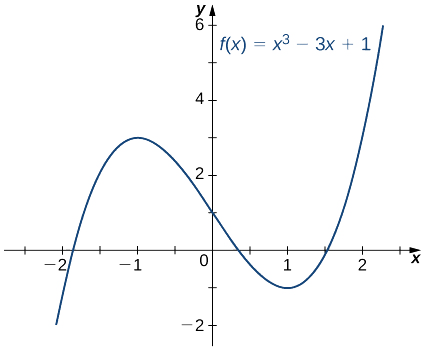
Se dibuja la función f (x) = x3 — 3x + 1. Tiene raíces entre −2 y −1, 0 y 1, y 1 y 2. — Figura\(\PageIndex{2}\): La función\(f(x)=x^3−3x+1\) tiene una raíz sobre el intervalo\([1,2].\)

Ejercicio\(\PageIndex{1}\)

Dejando\(x_0=0\), usemos el método de Newton para aproximar la raíz de\(f(x)=x^3−3x+1\) sobre el intervalo\([0,1]\) calculando\(x_1\) y\(x_2\).

Pista: Usa la ecuación\ ref {Newton}.

Responder: \(x_1≈0.33333333\)
\(x_2≈0.347222222\)

El método de Newton también se puede utilizar para aproximar raíces cuadradas. Aquí te mostramos cómo aproximar\(\sqrt{2}\). Este método se puede modificar para aproximar la raíz cuadrada de cualquier número positivo.

Ejemplo\(\PageIndex{2}\): Finding a Square Root

Utilice el método de Newton para aproximar\(\sqrt{2}\) (Figura\(\PageIndex{3}\)). Dejar\(f(x)=x^2−2\)\(x_0=2\), dejar y calcular\(x_1,\, x_2,\, x_3,\, x_4,\, x_5\). (Observamos que dado que\(f(x)=x^2−2\) tiene un cero at\(\sqrt{2}\), el valor inicial\(x_0=2\) es una opción razonable para aproximarse\(\sqrt{2}\)).

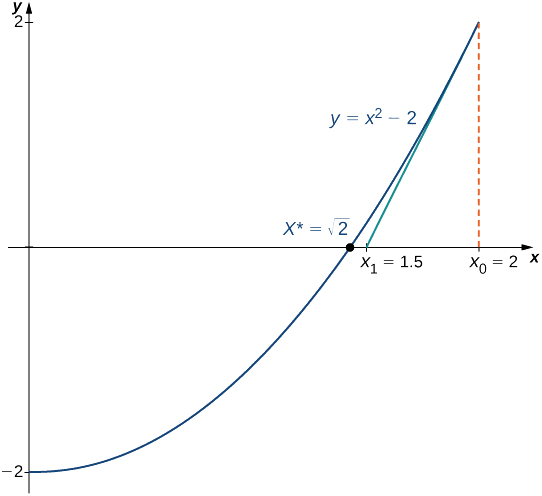
Se dibuja la función y = x2 — 2. Una línea discontinua sale de x0 = 2, y una línea tangente se dibuja hacia abajo desde allí. Toca x1 = 1.5, que está cerca de x* = la raíz cuadrada de 2. — Figura\(\PageIndex{3}\): Podemos usar el método de Newton para encontrar\(\sqrt{2}\).

Solución

Para\(f(x)=x^2−2,\; f′(x)=2x.\) De la ecuación\ ref {Newton}, sabemos que

\ [\ begin {alinear*} x_n&=x_ {n−1} −\ frac {f (x_ {n−1})} {f' (x_ {n−1})}\\ [4pt]
&=x_ {n−1} −\ frac {x^2_ {n−1} −2} {2x_ {n−1}}\ [4pt]
&=\ frac {1} {2} x_ {n−1} +\ frac {1} {x_ {n−1}}\\ [4pt]
&=\ frac {1} {2}\ izquierda (x_ {n−1} +\ frac {2} {x_ {n−1}}\ derecha). \ end {align*}\ nonumber\]

Por lo tanto,

\(x_1=\frac{1}{2}\left(x_0+\frac{2}{x_0}\right)=\frac{1}{2}\left(2+\frac{2}{2}\right)=1.5\)

\(x_2=\frac{1}{2}\left(x_1+\frac{2}{x_1}\right)=\frac{1}{2}\left(1.5+\frac{2}{1.5}\right)≈1.416666667.\)

Continuando de esta manera, encontramos que

\(x_1=1.5\)

\(x_2≈1.416666667\)

\(x_3≈1.414215686\)

\(x_4≈1.414213562\)

\(x_5≈1.414213562.\)

Dado que obtuvimos el mismo valor para\(x_4\) y\(x_5\), es poco probable que el valor\(x_n\) cambie en cualquier aplicación posterior del método de Newton. Concluimos que\(\sqrt{2}≈1.414213562.\)

Ejercicio\(\PageIndex{2}\)

Utilice el método de Newton para aproximar\(\sqrt{3}\) dejando\(f(x)=x^2−3\) y\(x_0=3\). Encontrar\(x_1\) y\(x_2\).

Pista: Para\(f(x)=x^2−3\), Ecuación\ ref {Newton} se reduce a\(x_n=\frac{x_{n−1}}{2}+\frac{3}{2x_{n−1}}\).

Responder: \(x_1=2\)
\(x_2=1.75\)

Cuando se usa el método de Newton, cada aproximación después de la suposición inicial se define en términos de la aproximación anterior usando la misma fórmula. En particular, al definir la función\(F(x)=x−\left[\frac{f(x)}{f′(x)}\right]\), podemos reescribir la Ecuación\ ref {Newton} como\(x_n=F(x_{n−1})\). Este tipo de proceso, donde cada uno\(x_n\) se define en términos de\(x_{n−1}\) repitiendo la misma función, es un ejemplo de un proceso iterativo. En breve, examinamos otros procesos iterativos. Primero, veamos las razones por las que el método de Newton podría fallar en encontrar una raíz.

Fallas del método de Newton

Por lo general, el método de Newton se utiliza para encontrar raíces con bastante rapidez. Sin embargo, las cosas pueden salir mal. Algunas razones por las que el método de Newton podría fallar incluyen las siguientes:

En una de las aproximaciones\(x_n\), la derivada\(f′\) es cero en\(x_n\), pero\(f(x_n)≠0\). Como resultado, la línea tangente de\(f\) at\(x_n\) no se cruza con el\(x\) eje. Por lo tanto, no podemos continuar el proceso iterativo.
Las aproximaciones\(x_0,\, x_1,\, x_2,\, …\) pueden acercarse a una raíz diferente. Si la función\(f\) tiene más de una raíz, es posible que nuestras aproximaciones no se acerquen a la que estamos buscando, sino que se acerquen a una raíz diferente (ver Figura\(\PageIndex{4}\)). Este evento ocurre con mayor frecuencia cuando no elegimos la aproximación lo suficientemente\(x_0\) cerca de la raíz deseada.
Las aproximaciones pueden no acercarse a una raíz por completo. En Ejemplo\(\PageIndex{3}\), proporcionamos un ejemplo de una función y una suposición inicial\(x_0\) tal que las aproximaciones sucesivas nunca se acercan a una raíz porque las aproximaciones sucesivas continúan alternando de un lado a otro entre dos valores.

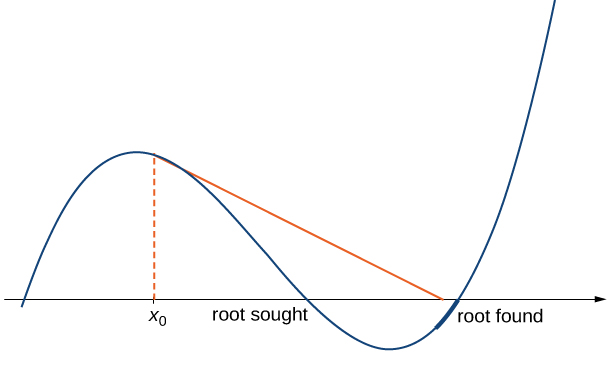
Se dibuja una función con dos raíces, etiquetadas raíz buscada y raíz encontrada. Se elige un punto x0 de tal manera que cuando se toma la tangente de x0, aunque esté más cerca de la raíz buscada, la tangente apunta a la raíz encontrada. — Figura\(\PageIndex{4}\): Si la suposición inicial\(x_0\) está demasiado lejos de la raíz buscada, puede llevar a aproximaciones que se acerquen a una raíz diferente.

Ejemplo\(\PageIndex{3}\): When Newton’s Method Fails

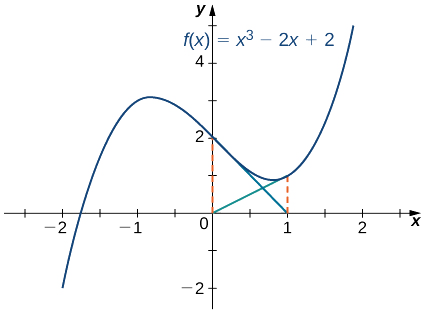
Considera la función\(f(x)=x^3−2x+2\). Vamos\(x_0=0\). Demostrar que la secuencia\(x_1,\, x_2,\, …\) no logra acercarse a una raíz de\(f\).

Solución

Para\(f(x)=x^3−2x+2,\) el derivado es\(f′(x)=3x^2−2\) .Por lo tanto,

\[x_1=x_0−\frac{f(x_0)}{f′(x_0)}=0−\frac{f(0)}{f′(0)}=−\frac{2}{−2}=1. \nonumber \]

En el siguiente paso,

\[x_2=x_1−\frac{f(x_1)}{f'(x_1)}=1−\frac{f(1)}{f′(1)}=1−\frac{1}{1}=0. \nonumber \]

En consecuencia, los números\(x_0,\, x_1,\, x_2,\, …\) continúan rebotando de un lado a otro entre\(0\)\(1\) y y nunca se acercan a la raíz de la\(f\) cual está sobre el intervalo\([−2,−1]\) (Figura\(\PageIndex{5}\)). Afortunadamente, si elegimos una aproximación inicial\(x_0\) más cercana a la raíz real, podemos evitar esta situación.

Se dibuja la función f (x) = x3 — 2x + 2, que tiene una raíz entre −2 y −1. La tangente de x = 0 va a x = 1, y la tangente de x = 1 va a x = 0. — Figura\(\PageIndex{5}\): Las aproximaciones continúan alternando entre\(0\) y\(1\) y nunca acercarse a la raíz de\(f\).

Ejercicio\(\PageIndex{3}\)

Para\(f(x)=x^3−2x+2,\) dejar\(x_0=−1.5\) y encontrar\(x_1\) y\(x_2\).

Pista: Usa la ecuación\ ref {Newton}.

Responder: \(x_1≈−1.842105263\)
\(x_2≈−1.772826920\)

De Example\(\PageIndex{3}\), vemos que el método de Newton no siempre funciona. Sin embargo, cuando funciona, la secuencia de aproximaciones se acerca a la raíz muy rápidamente. Las discusiones sobre la rapidez con la que la secuencia de aproximaciones se aproxima a una raíz encontrada usando el método de Newton se incluyen en textos sobre análisis numérico.

Otros procesos iterativos

Como se mencionó anteriormente, el método de Newton es un tipo de proceso iterativo. Ahora miramos un ejemplo de un tipo diferente de proceso iterativo.

Considera una función\(F\) y un número inicial\(x_0\). Defina los números subsiguientes\(x_n\) por la fórmula\(x_n=F(x_{n−1})\). Este proceso es un proceso iterativo que crea una lista de números\(x_0,\, x_1,\, x_2,\, …,\, x_n,\, ….\) Esta lista de números puede acercarse a un número finito a\(x^*\) medida que\(n\) se hace más grande, o puede que no. En Ejemplo\(\PageIndex{4}\), vemos un ejemplo de una función\(F\) y una suposición inicial\(x_0\) tal que la lista resultante de números se aproxima a un valor finito.

Ejemplo\(\PageIndex{4}\): Finding a Limit for an Iterative Process

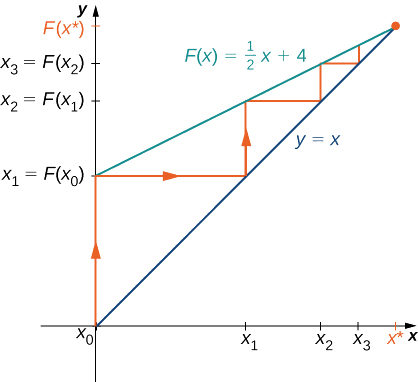
Dejar\(F(x)=\frac{1}{2}x+4\) y dejar\(x_0=0\). Para todos\(n≥1\), vamos\(x_n=F(x_{n−1})\). Encuentra los valores\(x_1,\, x_2,\, x_3,\, x_4,\, x_5\). Hacer una conjetura sobre lo que sucede con esta lista de números\(x_1,\, x_2,\, x_3,\, …,\, x_n,\, …\) como\(n→∞\). Si la lista de números\(x_1,\, x_2,\, x_3,\, …\) se acerca a un número finito\(x^*\), entonces\(x^*\) satisface\(x^*=F(x^*)\), y\(x^*\) se llama punto fijo de\(F\).

Solución

Si\(x_0=0\), entonces

\(x_1=\frac{1}{2}(0)+4=4\)
\(x_2=\frac{1}{2}(4)+4=6\)
\(x_3=\frac{1}{2}(6)+4=7\)
\(x_4=\frac{1}{2}(7)+4=7.5\)
\(x_5=\frac{1}{2}(7.5)+4=7.75\)
\(x_6=\frac{1}{2}(7.75)+4=7.875\)
\(x_7=\frac{1}{2}(7.875)+4=7.9375\)
\(x_8=\frac{1}{2}(7.9375)+4=7.96875\)
\(x _9=\frac{1}{2}(7.96875)+4=7.984375.\)

De esta lista, conjeturamos que los valores se\(x_n\) acercan\(8\).

La figura\(\PageIndex{6}\) proporciona un argumento gráfico que los valores se acercan\(8\) como\(n→∞\). Comenzando en el punto\((x_0,x_0)\), dibujamos una línea vertical al punto\((x_0,F(x_0))\). El siguiente número en nuestra lista es\(x_1=F(x_0)\). Utilizamos\(x_1\) para calcular\(x_2\). Por lo tanto, dibujamos una línea horizontal\((x_0,x_1)\) que se conecta al punto\((x_1,x_1)\) de la línea\(y=x\), y luego dibujamos una línea vertical\((x_1,x_1)\) que se conecta al punto\((x_1,F(x_1))\). La salida\(F(x_1)\) se convierte\(x_2\). Continuando de esta manera, podríamos crear un número infinito de segmentos de línea. Estos segmentos de línea están atrapados entre las líneas\(F(x)=\frac{x}{2}+4\) y\(y=x\). Los segmentos de línea se acercan al punto de intersección de estas dos líneas, lo que ocurre cuando\(x=F(x)\). Resolviendo la ecuación\(x=\frac{x}{2}+4,\) concluimos que se cruzan en\(x=8\). Por lo tanto, nuestra evidencia gráfica concuerda con nuestra evidencia numérica de que la lista de números\(x_0,\, x_1,\, x_2,\, …\) se aproxima\(x^*=8\) como\(n→∞\).

La función F (x) = (1/2) x + 4 se grafica junto con y = x Desde x0, que parece estar en el origen, se dibuja una línea a la función F (x) en x1 = F (x0). Después se dibuja una línea a la derecha desde aquí hasta la línea y = x, punto en el que se dibuja una línea hasta x2 = F (x1). Después se dibuja una línea a la derecha desde aquí hasta la línea y = x, punto en el que se dibuja una línea hasta x3 = F (x2). Continuando con este proceso convergería en el punto de intersección de las dos líneas en x* = 8. — Figura\(\PageIndex{6}\): Este proceso iterativo se acerca al valor\(x^*=8.\)

Ejercicio\(\PageIndex{4}\)

Considera la función\(F(x)=\frac{1}{3}x+6\). Dejar\(x_0=0\) y dejar\(x_n=F(x_{n−1})\) para\(n≥2\). Encontrar\(x_1,\, x_2,\, x_3,\, x_4,\, x_5\). Hacer una conjetura sobre lo que sucede con la lista de números\(x_1,\, x_2,\, x_3,\, …\, x_n,\, … \) como\(n→∞.\)

Pista: Considera el punto donde las líneas\(y=x\) y se\(y=F(x)\) cruzan.

Responder: \(x_1=6,\;x_2=8,\;x_3=\frac{26}{3},\;x_4=\frac{80}{9},\;x_5=\frac{242}{27};\;x^*=9\)

Procesos iterativos y Caos

Los procesos iterativos pueden producir un comportamiento muy interesante. En esta sección, hemos visto varios ejemplos de procesos iterativos que convergen a un punto fijo. También vimos en Ejemplo\(\PageIndex{3}\) que el proceso iterativo rebotó de un lado a otro entre dos valores. Llamamos a este tipo de comportamiento un ciclo de 2. Los procesos iterativos pueden converger en ciclos con diversas periodicidades, como 2 ciclos, 4 ciclos (donde el proceso iterativo repite una secuencia de cuatro valores), 8 ciclos, etc.

Algunos procesos iterativos producen lo que los matemáticos llaman caos. En este caso, el proceso iterativo salta de valor en valor de una manera aparentemente aleatoria y nunca converge ni se asienta en un ciclo. Si bien una exploración completa del caos está fuera del alcance de este texto, en este proyecto analizamos una de las propiedades clave de un proceso iterativo caótico: la dependencia sensible de las condiciones iniciales. Esta propiedad se refiere al concepto de que pequeños cambios en las condiciones iniciales pueden generar comportamientos drásticamente diferentes en el proceso iterativo.

Probablemente el ejemplo más conocido de caos es el conjunto de Mandelbrot (ver Figura\(\PageIndex{7}\)), que lleva el nombre de Benoit Mandelbrot (1924-2010), quien investigó sus propiedades y ayudó a popularizar el campo de la teoría del caos. El conjunto de Mandelbrot suele ser generado por computadora y muestra detalles fascinantes sobre la ampliación, incluida la autorreplicación del conjunto. Varias versiones coloridas del conjunto se han mostrado en museos y se pueden encontrar en línea y en libros populares sobre el tema.

Un fractal muy complicado y de aspecto orgánico. — Figura\(\PageIndex{7}\): El conjunto Mandelbrot es un ejemplo bien conocido de un conjunto de puntos generados por el comportamiento caótico iterativo de una función relativamente simple.

En este proyecto utilizamos el mapa logístico

\[f(x)=rx(1−x) \nonumber \]

dónde\(x∈[0,1]\) y\(r>0\)

como la función en nuestro proceso iterativo. El mapa logístico es una función engañosamente simple; pero, dependiendo del valor de\(r\), el proceso iterativo resultante muestra algún comportamiento muy interesante. Puede conducir a puntos fijos, ciclos, e incluso caos.

Para visualizar el comportamiento a largo plazo del proceso iterativo asociado al mapa logístico, utilizaremos una herramienta llamada diagrama telaraña. Como hicimos con el proceso iterativo que examinamos anteriormente en esta sección, primero dibujamos una línea vertical del punto\((x_0,0)\) al punto\((x_0,f(x_0))=(x_0,x_1)\). Luego dibujamos una línea horizontal desde ese punto hasta el punto,\((x_1,x_1),\) luego dibujamos una línea vertical hasta\((x_1,f(x_1))=(x_1,x_2)\), y continuamos el proceso hasta que se haga evidente el comportamiento a largo plazo del sistema. La figura\(\PageIndex{8}\) muestra el comportamiento a largo plazo del mapa logístico cuando\(r=3.55\) y\(x_0=0.2\). (Las primeras\(100\) iteraciones no se trazan.) El comportamiento a largo plazo de este proceso iterativo es un\(8\) ciclo.

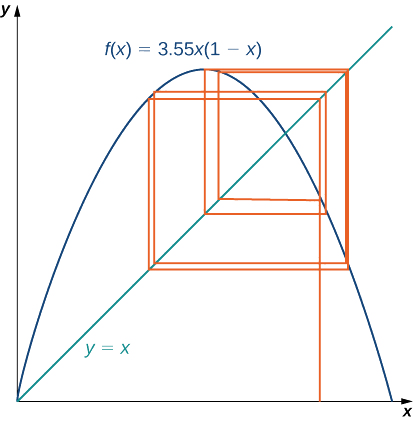
En el primer cuadrante, f (x) = 3.55x (1 — x) se grafica como es y = x. Desde algún punto del eje x, se dibuja una línea hasta la línea y = x, punto en el que gira para ser horizontal y continúa hasta tocar el borde exterior de f (x), punto en el que vuelve a ser vertical hasta que cada uno la línea y = x Esta proceso continúa varias veces y crea una serie interesante de cajas. — Figura\(\PageIndex{8}\): Aquí se presenta un diagrama de telaraña para\(f(x)=3.55x(1−x)\). La secuencia de valores da como resultado un ciclo de 8.

Deja\(r=0.5\) y elige\(x_0=0.2\). Ya sea a mano o usando una computadora, calcule los primeros\(10\) valores de la secuencia. ¿La secuencia parece converger? Si es así, ¿a qué valor? ¿Resulta en un ciclo? Si es así, ¿qué tipo de ciclo (por ejemplo,\(2\) −ciclo,\(4\) −ciclo.)?
¿Qué pasa cuando\(r=2\)?
Para\(r=3.2\) y\(r=3.5\), calcular los valores de la primera\(100\) secuencia. Generar un diagrama telaraña para cada proceso iterativo. (Varios applets gratuitos están disponibles en línea que generan diagramas de telaraña para el mapa logístico). ¿Cuál es el comportamiento a largo plazo en cada uno de estos casos?
Ahora vamos a\(r=4.\) Calcular los primeros valores de\(100\) secuencia y generar un diagrama de telaraña. ¿Cuál es el comportamiento a largo plazo en este caso?
Repite el proceso para\(r=4,\) pero deja\(x_0=0.201.\) ¿Cómo se compara este comportamiento con el comportamiento para\(x_0=0.2\)?

Conceptos clave

El método de Newton aproxima las raíces\(f(x)=0\) de comenzando con una aproximación inicial\(x_0\), luego usa líneas tangentes a la gráfica de\(f\) para crear una secuencia de aproximaciones\(x_1,\, x_2,\, x_3,\, ….\)
Por lo general, el método de Newton es un método eficiente para encontrar una raíz en particular. En ciertos casos, el método de Newton no funciona porque la lista de números\(x_0,\, x_1,\, x_2,\, …\) no se acerca a un valor finito o se acerca a un valor distinto de la raíz buscada.
Cualquier proceso en el que\(x_0,\, x_1,\, x_2,\, …\) se genera una lista de números definiendo un número inicial\(x_0\) y definiendo los números subsiguientes por la ecuación\(x_n=F(x_{n−1})\) para alguna función\(F\) es un proceso iterativo. El método de Newton es un ejemplo de un proceso iterativo, donde la función\(F(x)=x−\left[\frac{f(x)}{f′(x)}\right]\) para una función dada\(f\).

Glosario

proceso iterativo: proceso en el que\(x_0,x_1,x_2,x_3…\) se genera una lista de números comenzando con un número\(x_0\) y definiendo\(x_n=F(x_{n−1})\) para\(n≥1\)

Método de Newton: método para aproximar raíces de\(f(x)=0;\) usar una suposición inicial\(x_0\); cada aproximación posterior se define por la ecuación\(x_n=x_{n−1}−\frac{f(x_{n−1})}{f'(x_{n−1})}\)