8.2E: Ejercicios para la Sección 8.2

Última actualización
Guardar como PDF

Page ID: 116277

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Para los ejercicios 1 - 3, utilice el campo de dirección a continuación de la ecuación diferencial$ y'=−2y.$ Dibuje la gráfica de la solución para las condiciones iniciales dadas.

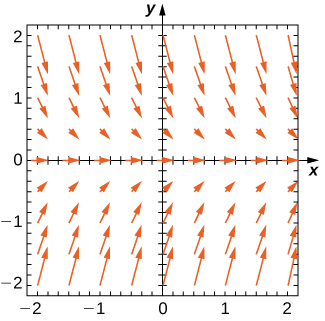
$Un campo de dirección con flechas horizontales apuntando a la derecha en 0. Las flechas sobre el eje x apuntan hacia abajo y hacia la derecha. Cuanto más lejos del eje x, más pronunciadas son las flechas, y cuanto más cerca del eje x, más planas son las flechas. De igual manera, las flechas debajo del eje x apuntan hacia arriba y hacia la derecha. Cuanto más lejos del eje x, más pronunciadas son las flechas, y cuanto más cerca del eje x, más planas son las flechas.$

1)$ y(0)=1$

2)$ y(0)=0$

Contestar: 0. Cuanto más cerca están del eje x, más horizontales están las flechas, y cuanto más lejos están, más verticales se vuelven." style="width: 325px; height: 321px;" width="325px" height="321px" src="https://math.libretexts.org/@api/dek...08_02_203.jpeg">

3)$ y(0)=−1$

4) ¿Hay algún equilibrio entre las soluciones de la ecuación diferencial a partir de los ejercicios 1 - 3? Enumere cualquier equilibrio junto con sus estabilidades.

Contestar: $ y=0$es un equilibrio estable

Para los ejercicios 5 - 7, use el campo de dirección a continuación de la ecuación diferencial$ y'=y^2−2y$. Dibuje la gráfica de la solución para las condiciones iniciales dadas.

Un campo de dirección con flechas horizontales en y = 0 e y = 2. Las flechas apuntan hacia arriba para y 2 y para y < 0. Las flechas apuntan hacia abajo para 0 < y < 2. Cuanto más cerca están las flechas de estas líneas, más horizontales están, y cuanto más alejadas, más verticales están las flechas." style="width: 325px; height: 321px;" width="325px" height="321px" src="https://math.libretexts.org/@api/dek...08_02_205.jpeg">

5)$ y(0)=3$

6)$ y(0)=1$

Contestar: 2 y para y < 0. Las flechas apuntan hacia abajo para 0 < y < 2. Cuanto más cerca están las flechas de estas líneas, más horizontales están, y cuanto más alejadas, más verticales están las flechas. Se esboza una solución que sigue y = 2 en el cuadrante dos, pasa por (0, 1), y luego sigue el eje x." style="width: 319px; height: 320px;" width="319px" height="320px" src="https://math.libretexts.org/@api/dek...08_02_207.jpeg">

7)$ y(0)=−1$

8) ¿Hay algún equilibrio entre las soluciones de la ecuación diferencial a partir de los ejercicios 5 a 7? Enumere cualquier equilibrio junto con sus estabilidades.

Contestar: $ y=0$es un equilibrio estable y$ y=2$ es inestable

En los ejercicios 9 - 13, dibuja el campo de dirección para las siguientes ecuaciones diferenciales, luego resuelve la ecuación diferencial. Dibuja tu solución en la parte superior del campo de dirección. ¿Su solución sigue las flechas en su campo de dirección?

9)$ y'=t^3$

10)$ y'=e^t$

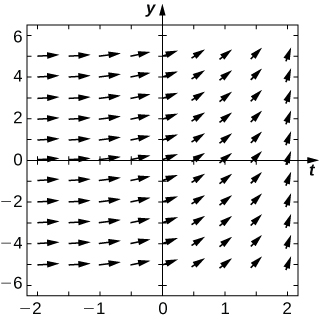
Contestar: $Un campo de dirección sobre los cuatro cuadrantes. A medida que t va de 0 a infinito, las flechas se vuelven cada vez más verticales después de estar horizontales más cerca de x = 0.$

11)$ \dfrac{dy}{dx}=x^2\cos x$

12)$ \dfrac{dy}{dt}=te^t$

Contestar: $Un campo de dirección sobre [-2, 2] en los ejes x e y. Las flechas apuntan ligeramente hacia abajo y a la derecha sobre [-2, 0] y gradualmente se vuelven verticales sobre [0, 2].$

13)$ \dfrac{dx}{dt}=\cosh(t)$

En los ejercicios 14 - 18, dibuje el campo direccional para las siguientes ecuaciones diferenciales. ¿Qué se puede decir sobre el comportamiento de la solución? ¿Hay equilibrios? ¿Qué estabilidad tienen estos equilibrios?

14)$ y'=y^2−1$

Contestar: Parece haber eculibrios en$y = -1$ (estable) e$y = 1$ (inestable).
1. Las flechas apuntan hacia abajo para -1 < y < 1. Cuanto más cerca están las flechas de estas líneas, más horizontales están, y cuanto más lejos están, más verticales están." style="width: 342px; height: 344px;" width="342px" height="344px" src="https://math.libretexts.org/@api/dek...08_02_214.jpeg">

15)$ y'=y−x$

16)$ y'=1−y^2−x^2$

Contestar: No parece haber ningún equilibrio.
$Un campo de dirección con flechas apuntando hacia abajo y hacia la derecha para casi todos los puntos en [-2, 2] en los ejes x e y. Cerca del origen, las flechas se vuelven más horizontales, apuntan hacia la parte superior derecha, se vuelven más horizontales y luego apuntan hacia abajo a la derecha nuevamente.$

17)$ y'=t^2\sin y$

18)$ y'=3y+xy$

Contestar: Parece haber un equilibrio inestable en$y=0.$
-3, las flechas apuntan hacia arriba. Debajo del eje x y para x < -3, las flechas apuntan hacia arriba. Para x > -3, las flechas apuntan hacia abajo. Cuanto más lejos del eje x y x = -3, las flechas se vuelven más verticales, y cuanto más cerca se acercan, más horizontales se vuelven." style="width: 405px; height: 344px;" width="405px" height="344px" src="https://math.libretexts.org/@api/dek...08_02_218.jpeg">

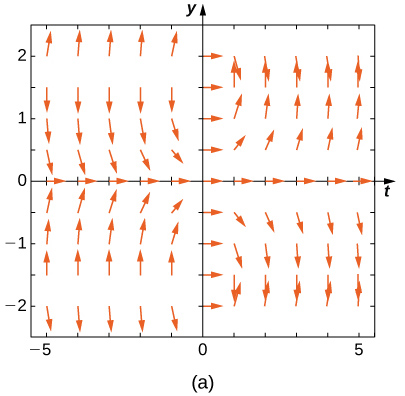
Haga coincidir el campo de dirección con las ecuaciones diferenciales dadas. Explica tus selecciones.

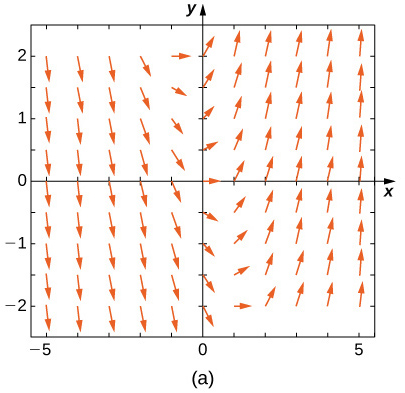
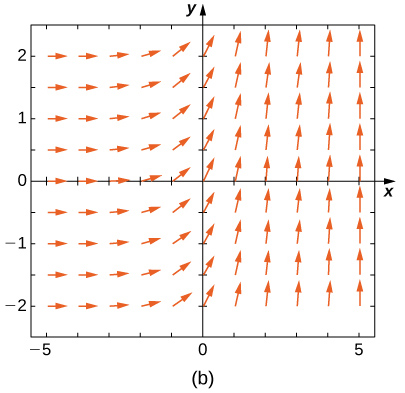
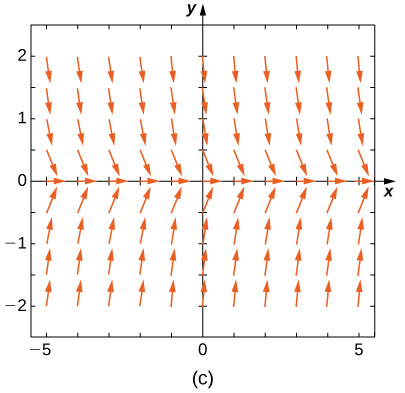
$Un campo de dirección con flechas apuntando hacia abajo y a la derecha en los cuadrantes dos y tres. Después de cruzar el eje y, las flechas cambian de dirección y apuntan hacia la derecha.$ $Un campo de dirección con flechas horizontales apuntando a la izquierda en los cuadrantes dos y tres. Al cruzar el eje y, las flechas cambian y apuntan hacia arriba en los cuadrantes uno y cuatro.$ $Un campo de dirección con flechas horizontales apuntando a la derecha en el eje x. Arriba, las flechas apuntan hacia abajo y hacia la derecha, y abajo, las flechas apuntan hacia arriba y hacia la derecha. 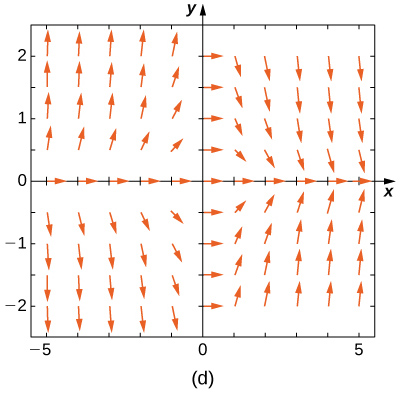Cuanto más lejos del eje x, más verticales se vuelven las flechas.$ $Un campo de dirección con flechas horizontales en los ejes x e y. Las flechas apuntan hacia abajo y a la derecha en los cuadrantes uno y tres. 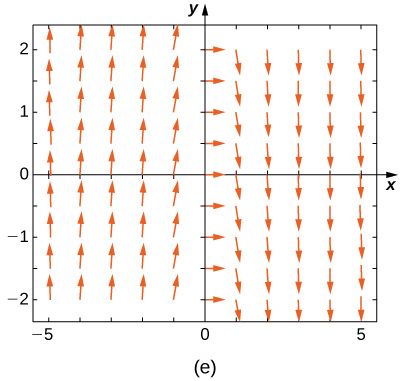Señalan hacia arriba y a la derecha en los cuadrantes dos y cuatro.$ $Un campo de dirección con flechas apuntando hacia arriba en los cuadrantes dos y tres, a la derecha en el eje y, y hacia abajo en los cuadrantes uno y cuatro.$

19)$ y'=−3y$

20)$ y'=−3t$

Contestar: $ E$

21)$ y'=e^t$

22)$ y'=\frac{1}{2}y+t$

Contestar: $ A$

23)$ y'=−ty$

Haga coincidir el campo de dirección con las ecuaciones diferenciales dadas. Explica tus selecciones.

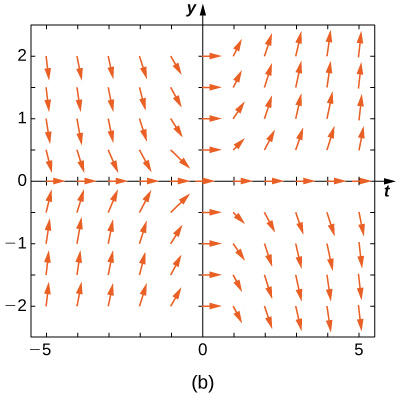
$Un campo de dirección con flechas horizontales apuntando a la derecha en los ejes x e y. En los cuadrantes uno y tres, las flechas apuntan hacia arriba, y en los cuadrantes dos y cuatro, apuntan hacia abajo.$ $Un campo de dirección con flechas horizontales apuntando a la derecha en los ejes x e y. 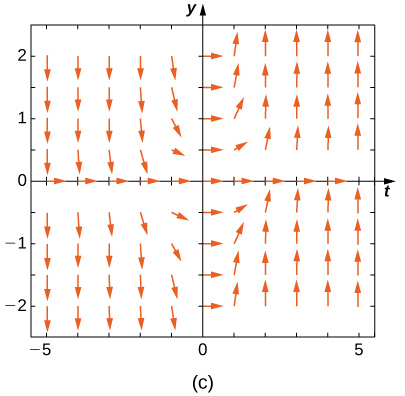En los cuadrantes uno y tres, las flechas apuntan hacia arriba y hacia la derecha, y en los cuadrantes dos y cuatro, las flechas apuntan hacia abajo y hacia la derecha.$ $Un campo de dirección con flechas horizontales apuntando a la derecha en los ejes x e y. 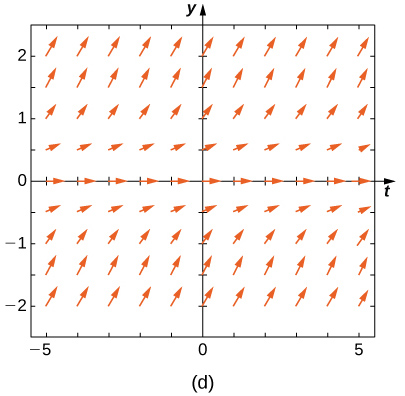En los cuadrantes dos y tres, las flechas apuntan hacia abajo, y en los cuadrantes uno y cuatro, las flechas apuntan hacia arriba.$ $Un campo de dirección con flechas horizontales apuntando a la derecha en el eje x. Las flechas apuntan hacia arriba y hacia la derecha en todos los cuadrantes. Cuanto más cerca están las flechas del eje x, más horizontales están las flechas, y cuanto más alejadas están, más verticales están.$ Un campo de dirección con flechas horizontales en el eje y. Las flechas también son más horizontales más cercanas a y = 1.5, y = -1.5, y el eje y. Para y 1.5 y x < 0, para y < -1.5 y x < 0, y para -1.5 < y < 1.5 and x > 0-, las flechas apuntan hacia abajo. Para y> 1.5 y x > 0, para y < -1.5, para y < -1.5 and x > 0, y para -1.5 < y < 1.5 y x < 0, las flechas apuntan hacia arriba." style="width: 405px; height: 380px;" width="405px" height="380px" src="https://math.libretexts.org/@api/dek...8_02_220e.jpeg">

24)$ y'=t\sin y$

Contestar: $ B$

25)$ y'=−t\cos y$

26)$ y'=t\tan y$

Contestar: $ A$

27)$ y'=\sin^2y$

28)$ y'=y^2t^3$

Contestar: $ C$

Estima las siguientes soluciones usando el método de Euler con$ n=5$ pasos a lo largo del intervalo$ t=[0,1].$ Si eres capaz de resolver exactamente el problema del valor inicial, compara tu solución con la solución exacta. Si no puede resolver el problema del valor inicial, se le proporcionará la solución exacta para que la compare con el método de Euler. ¿Qué tan preciso es el método de Euler?

29)$ y'=−3y,\quad y(0)=1$

30)$ y'=t^2,\quad y(0)=1$

Contestar: $ 2.24,$exacta:$ 3$

Solución:

31)$ y′=3t−y,\quad y(0)=1.$ La solución exacta es$ y=3t+4e^{−t}−3$

32)$ y′=y+t^2,\quad y(0)=3.$ La solución exacta es$ y=5e^t−2−t^2−2t$

Contestar: $ 7.739364,$exacta:$ 5(e−1)$

33)$ y′=2t,\quad y(0)=0$

34) [T]$ y'=e^{x+y},y(0)=−1.$ La solución exacta es$ y=−\ln(e+1−e^x)$

Contestar: $ −0.2535,$exacta:$ 0$

35)$ y′=y^2\ln(x+1),\quad y(0)=1.$ La solución exacta es$ y=−\dfrac{1}{(x+1)(\ln(x+1)−1)}$

36)$ y′=2^x,\quad y(0)=0.$ La solución exacta es$ y=\dfrac{2^x−1}{\ln 2}$

Contestar: $ 1.345,$exacta:$ \frac{1}{\ln(2)}$

37)$ y′=y,\quad y(0)=−1.$ La solución exacta es$ y=−e^x$.

38)$ y′=−5t,\quad y(0)=−2.$ La solución exacta es$ y=−\frac{5}{2}t^2−2$

Contestar: $ −4,$exacta:$ −1/2$

Las ecuaciones diferenciales se pueden utilizar para modelar epidemias de enfermedades. En el siguiente conjunto de problemas, examinamos el cambio de tamaño de dos subpoblaciones de personas que viven en una ciudad: individuos infectados y individuos susceptibles a la infección. $ S$representa el tamaño de la población susceptible y$ I$ representa el tamaño de la población infectada. Suponemos que si una persona susceptible interactúa con una persona infectada, existe la probabilidad de$ c$ que la persona susceptible se infecte. Cada persona infectada se recupera de la infección a un ritmo$ r$ y vuelve a ser susceptible. Consideramos el caso de la influenza, donde asumimos que nadie muere por la enfermedad, por lo que asumimos que el tamaño total de la población de las dos subpoblaciones es un número constante,$ N$. Las ecuaciones diferenciales que modelan estos tamaños de población son

$ S'=rI−cSI$y$ I'=cSI−rI.$

Aquí$ c$ representa la tasa de contacto y$ r$ es la tasa de recuperación.

39) Demostrar que, por nuestra suposición de que el tamaño total de la población es constante, se$ (S+I=N),$ puede reducir el sistema a una sola ecuación diferencial en$ I:I'=c(N−I)I−rI.$

40) Suponiendo que los parámetros son$ c=0.5,N=5,$ y$ r=0.5$, dibuje el campo direccional resultante.

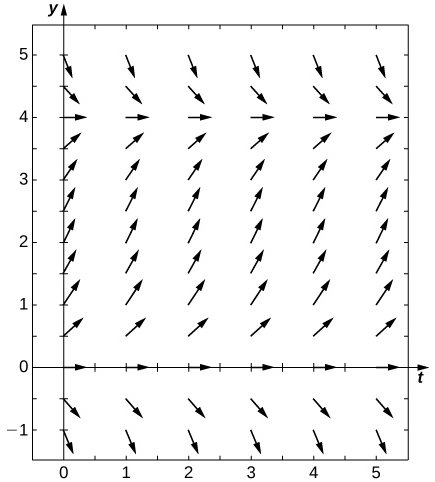
Contestar: $Un campo de dirección con flechas horizontales apuntando a la derecha en el eje x y en y = 4. Las flechas debajo del eje x y arriba y = 4 apuntan hacia abajo y hacia la derecha. Las flechas entre el eje x y y = 4 apuntan hacia arriba y hacia la derecha.$

41) [T] Utilice un software computacional o una calculadora para calcular la solución al problema del valor inicial$ y'=ty,y(0)=2$ usando el Método de Euler con el tamaño de paso dado$ h$. Encuentre la solución en$ t=1$. Para una pista, aquí está “pseudo-código” sobre cómo escribir un programa de computadora para realizar el Método de Euler para$ y'=f(t,y),y(0)=2:$

Crear función$ f(t,y)$

Definir parámetros tamaño de$ y(1)=y_0,t(0)=0,$ paso$ h$, y número total de pasos,$ N$

Escribe un for-loop:

$ k=1$para$ N$

$ fn=f(t(k),y(k))$

$ y(k+1)=y(k)+h*fn$

$ t(k+1)=t(k)+h$

42) Resolver el problema del valor inicial para la solución exacta.

Contestar: $ y'=2e^{t^2/2}$

43) Dibuja el campo direccional

44)$ h=1$

Contestar: $ 2$

45) [T]$ h=10$

46) [T]$ h=100$

Contestar: $ 3.2756$

47) [T]$ h=1000$

48) [T] Evaluar la solución exacta en$ t=1$. Hacer una tabla de errores para el error relativo entre la solución del método de Euler y la solución exacta. ¿Cuánto cambia el error? ¿Se puede explicar?

Contestar

Solución exacta: y =$ 2\sqrt{e}.$

Tamaño del Paso	Error
$ h=1$	$ 0.3935$
$ h=10$	$ 0.06163$
$ h=100$	$ 0.006612$
$ h=10000$	$ 0.0006661$

Para los ejercicios 49 - 53, considere el problema del valor inicial$ y'=−2y,$ con$y(0)=2.$

49) Demostrar que$ y=2e^{−2x}$ resuelve este problema de valor inicial.

50) Dibujar el campo direccional de esta ecuación diferencial.

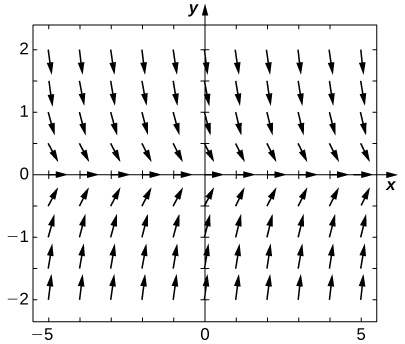
Contestar: $Campo de dirección para la ecuación diferencial y' = -2y. Un campo de dirección con flechas horizontales apuntando a la derecha en el eje x. Por encima del eje x, las flechas apuntan hacia abajo y hacia la derecha. Debajo del eje x, las flechas apuntan hacia arriba y hacia la derecha. Cuanto más cerca están las flechas del eje x, más horizontales están las flechas, y cuanto más alejadas están del eje x, más verticales son las flechas.$

51) [T] A mano o por calculadora o computadora, aproximar la solución usando el Método de Euler al$ t=10$ usar$ h=5$.

52) [T] Por calculadora o computadora, aproximar la solución usando el Método de Euler al$ t=10$ usar$ h=100.$

Contestar: $ 4.0741e^{−10}$

53) [T] Trazar la respuesta exacta y cada aproximación de Euler (para$ h=5$ y$ h=100$) a cada h en el campo direccional. ¿Qué notas?

Tamaño del Paso	Error
\( h=1\)	\( 0.3935\)
\( h=10\)	\( 0.06163\)
\( h=100\)	\( 0.006612\)
\( h=10000\)	\( 0.0006661\)

Search

Text Color

Text Size

Margin Size

Font Type