11.1: Ecuaciones paramétricas
- Page ID
- 116196
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Trazar una curva descrita por ecuaciones paramétricas.
- Convertir las ecuaciones paramétricas de una curva en la forma\(y=f(x)\).
- Reconocer las ecuaciones paramétricas de curvas básicas, como una línea y un círculo.
- Reconocer las ecuaciones paramétricas de un cicloide.
En esta sección examinamos las ecuaciones paramétricas y sus gráficas. En el sistema de coordenadas bidimensionales, las ecuaciones paramétricas son útiles para describir curvas que no son necesariamente funciones. El parámetro es una variable independiente que tanto\(x\) y\(y\) depende de, y a medida que aumenta el parámetro, los valores de\(x\) y\(y\) trazan una trayectoria a lo largo de una curva plana. Por ejemplo, si el parámetro es\(t\) (una opción común), entonces\(t\) podría representar el tiempo. Entonces\(x\) y\(y\) se definen como funciones del tiempo, y\((x(t),y(t))\) pueden describir la posición en el plano de un objeto dado a medida que se mueve a lo largo de un camino curvo.
Ecuaciones paramétricas y sus gráficas
Considera la órbita de la Tierra alrededor del Sol. Nuestro año dura aproximadamente 365.25 días, pero para esta discusión utilizaremos 365 días. El 1 de enero de cada año, la ubicación física de la Tierra con respecto al Sol es casi la misma, a excepción de los años bisiestos, cuando el rezago introducido por el\(\frac{1}{4}\) día extra del tiempo en órbita se integra en el calendario. Llamamos al 1 de enero “día 1” del año. Entonces, por ejemplo, el día 31 es el 31 de enero, el día 59 es el 28 de febrero, y así sucesivamente.
El número del día en un año puede considerarse una variable que determina la posición de la Tierra en su órbita. A medida que la Tierra gira alrededor del Sol, su ubicación física cambia en relación con el Sol. Después de un año completo, estamos de vuelta donde empezamos, y comienza un nuevo año. Según las leyes del movimiento planetario de Kepler, la forma de la órbita es elíptica, con el Sol en un foco de la elipse. Estudiamos esta idea con más detalle en Secciones Cónicas.
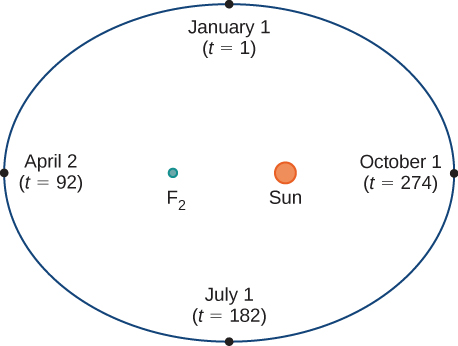
La figura\( \PageIndex{1}\) representa la órbita de la Tierra alrededor del Sol durante un año. El punto etiquetado\(F_2\) es uno de los focos de la elipse; el otro foco está ocupado por el Sol. Si superponemos ejes de coordenadas sobre esta gráfica, entonces podemos asignar pares ordenados a cada punto de la elipse (Figura\( \PageIndex{2}\)). Entonces cada\(x\) valor en la gráfica es un valor de posición en función del tiempo, y cada\(y\) valor es también un valor de posición en función del tiempo. Por lo tanto, cada punto de la gráfica corresponde a un valor de la posición de la Tierra en función del tiempo.
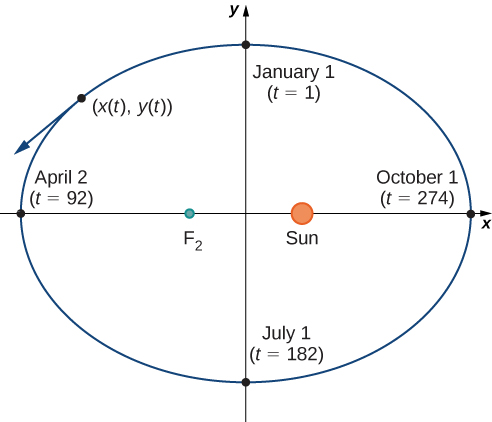
Podemos determinar las funciones para\(x(t)\) y\(y(t)\), con ello parametrizar la órbita de la Tierra alrededor del Sol. La variable\(t\) se denomina parámetro independiente y, en este contexto, representa el tiempo relativo al inicio de cada año.
Una curva en el\((x,y)\) plano se puede representar paramétricamente. Las ecuaciones que se utilizan para definir la curva se denominan ecuaciones paramétricas.
Si\(x\) y\(y\) son funciones continuas de\(t\) en un intervalo\(I\), entonces las ecuaciones
\[x=x(t) \nonumber \]
y
\[y=y(t) \nonumber \]
se llaman ecuaciones paramétricas y\(t\) se llama el parámetro. El conjunto de puntos\((x,y)\) obtenidos a medida que\(t\) varía a lo largo del intervalo\(I\) se denomina gráfico de las ecuaciones paramétricas. La gráfica de ecuaciones paramétricas se denomina curva paramétrica o curva plana, y se denota por\(C\).
Observe en esta definición que\(x\) y se\(y\) utilizan de dos maneras. El primero es como funciones de la variable independiente\(t\). Como\(t\) varía a lo largo del intervalo\(I\), las funciones\(x(t)\) y\(y(t)\) generan un conjunto de pares ordenados\((x,y)\). Este conjunto de pares ordenados genera la gráfica de las ecuaciones paramétricas. En este segundo uso, para designar los pares ordenados,\(x\) y\(y\) son variables. Es importante distinguir las variables\(x\) y\(y\) de las funciones\(x(t)\) y\(y(t)\).
Esboce las curvas descritas por las siguientes ecuaciones paramétricas:
- \(x(t)=t−1, \quad y(t)=2t+4,\quad \text{for }−3≤t≤2\)
- \(x(t)=t^2−3, \quad y(t)=2t+1,\quad \text{for }−2≤t≤3\)
- \(x(t)=4 \cos t, \quad y(t)=4 \sin t,\quad \text{for }0≤t≤2π\)
Solución
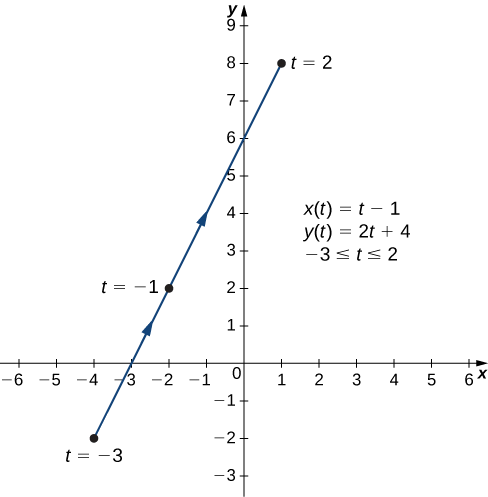
a. Para crear una gráfica de esta curva, primero establezca una tabla de valores. Dado que la variable independiente en ambos\(x(t)\) y\(y(t)\) es\(t\), vamos a\(t\) aparecer en la primera columna. Después\(x(t)\) y\(y(t)\) aparecerá en la segunda y tercera columnas de la tabla.
| \(t\) | \(x(t)\) | \(y(t)\) |
|---|---|---|
| \ (t\)” style="vertical-align:middle; ">−3 | \ (x (t)\)” style="vertical-align:middle; ">−4 | \ (y (t)\)” style="vertical-align:middle; ">−2 |
| \ (t\)” style="vertical-align:middle; ">−2 | \ (x (t)\)” style="vertical-align:middle; ">−3 | \ (y (t)\)” style="vertical-align:middle; ">0 |
| \ (t\)” style="vertical-align:middle; ">−1 | \ (x (t)\)” style="vertical-align:middle; ">−2 | \ (y (t)\)” style="vertical-align:middle; ">2 |
| \ (t\)” style="vertical-align:middle; ">0 | \ (x (t)\)” style="vertical-align:middle; ">−1 | \ (y (t)\)” style="vertical-align:middle; ">4 |
| \ (t\)” style="vertical-align:middle; ">1 | \ (x (t)\)” style="vertical-align:middle; ">0 | \ (y (t)\)” style="vertical-align:middle; ">6 |
| \ (t\)” style="vertical-align:middle; ">2 | \ (x (t)\)” style="vertical-align:middle; ">1 | \ (y (t)\)” style="vertical-align:middle; ">8 |
La segunda y tercera columnas de esta tabla proporcionan un conjunto de puntos a trazar. La gráfica de estos puntos aparece en la Figura\( \PageIndex{3}\). Las flechas en la gráfica indican la orientación de la gráfica, es decir, la dirección que un punto se mueve sobre la gráfica a medida que t varía de −3 a 2.
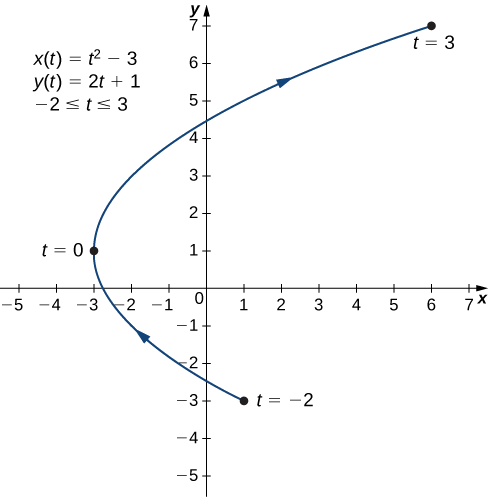
b. Para crear una gráfica de esta curva, vuelva a configurar una tabla de valores.
| \(t\) | \(x(t)\) | \(y(t)\) |
|---|---|---|
| \ (t\)” style="vertical-align:middle; ">−2 | \ (x (t)\)” style="vertical-align:middle; ">1 | \ (y (t)\)” style="vertical-align:middle; ">−3 |
| \ (t\)” style="vertical-align:middle; ">−1 | \ (x (t)\)” style="vertical-align:middle; ">−2 | \ (y (t)\)” style="vertical-align:middle; ">−1 |
| \ (t\)” style="vertical-align:middle; ">0 | \ (x (t)\)” style="vertical-align:middle; ">−3 | \ (y (t)\)” style="vertical-align:middle; ">1 |
| \ (t\)” style="vertical-align:middle; ">1 | \ (x (t)\)” style="vertical-align:middle; ">−2 | \ (y (t)\)” style="vertical-align:middle; ">3 |
| \ (t\)” style="vertical-align:middle; ">2 | \ (x (t)\)” style="vertical-align:middle; ">1 | \ (y (t)\)” style="vertical-align:middle; ">5 |
| \ (t\)” style="vertical-align:middle; ">3 | \ (x (t)\)” style="vertical-align:middle; ">6 | \ (y (t)\)” style="vertical-align:middle; ">7 |
La segunda y tercera columnas de esta tabla dan un conjunto de puntos a trazar (Figura\( \PageIndex{4}\)). El primer punto de la gráfica (correspondiente a\(t=−2\)) tiene coordenadas\((1,−3)\), y el último punto (correspondiente a\(t=3\)) tiene coordenadas\((6,7)\). \(t\)A medida que avanza de\(−2\) a\(3\), el punto de la curva viaja a lo largo de una parábola. La dirección que mueve el punto vuelve a llamarse orientación y se indica en la gráfica.
c. En este caso, utilice múltiplos de\(π/6\) for\(t\) y cree otra tabla de valores:
| \(t\) | \(x(t)\) | \(y(t)\) | \(t\) | \(x(t)\) | \(y(t)\) |
|---|---|---|---|---|---|
| \ (t\)” style="vertical-align:middle; ">0 | \ (x (t)\)” style="vertical-align:middle; ">4 | \ (y (t)\)” style="vertical-align:middle; ">0 | \ (t\)” style="vertical-align:middle; ">\(\frac{7π}{6}\) | \ (x (t)\)” style="vertical-align:middle; ">\(-2\sqrt{3}≈−3.5\) | \ (y (t)\)” style="vertical-align:middle; ">-2 |
| \ (t\)” style="vertical-align:middle; ">\(\frac{π}{6}\) | \ (x (t)\)” style="vertical-align:middle; ">\(2\sqrt{3}≈3.5\) | \ (y (t)\)” style="vertical-align:middle; ">2 | \ (t\)” style="vertical-align:middle; ">\(\frac{4π}{3}\) | \ (x (t)\)” style="vertical-align:middle; ">−2 | \ (y (t)\)” style="vertical-align:middle; ">\(−2\sqrt{3}≈−3.5\) |
| \ (t\)” style="vertical-align:middle; ">\(\frac{π}{3}\) | \ (x (t)\)” style="vertical-align:middle; ">2 | \ (y (t)\)” style="vertical-align:middle; ">\(2\sqrt{3}≈3.5\) | \ (t\)” style="vertical-align:middle; ">\(\frac{3π}{2}\) | \ (x (t)\)” style="vertical-align:middle; ">0 | \ (y (t)\)” style="vertical-align:middle; ">−4 |
| \ (t\)” style="vertical-align:middle; ">\(\frac{π}{2}\) | \ (x (t)\)” style="vertical-align:middle; ">0 | \ (y (t)\)” style="vertical-align:middle; ">4 | \ (t\)” style="vertical-align:middle; ">\(\frac{5π}{3}\) | \ (x (t)\)” style="vertical-align:middle; ">2 | \ (y (t)\)” style="vertical-align:middle; ">\(−2\sqrt{3}≈−3.5\) |
| \ (t\)” style="vertical-align:middle; ">\(\frac{2π}{3}\) | \ (x (t)\)” style="vertical-align:middle; ">−2 | \ (y (t)\)” style="vertical-align:middle; ">\(2\sqrt{3}≈3.5\) | \ (t\)” style="vertical-align:middle; ">\(\frac{11π}{6}\) | \ (x (t)\)” style="vertical-align:middle; ">\(2\sqrt{3}≈3.5\) | \ (y (t)\)” style="vertical-align:middle; ">-2 |
| \ (t\)” style="vertical-align:middle; ">\(\frac{5π}{6}\) | \ (x (t)\)” style="vertical-align:middle; ">\(−2\sqrt{3}≈−3.5\) | \ (y (t)\)” style="vertical-align:middle; ">2 | \ (t\)” style="vertical-align:middle; ">\(2π\) | \ (x (t)\)” style="vertical-align:middle; ">4 | \ (y (t)\)” style="vertical-align:middle; ">0 |
| \ (t\)” style="vertical-align:middle; ">\(π\) | \ (x (t)\)” style="vertical-align:middle; ">−4 | \ (y (t)\)” style="vertical-align:middle; ">0 | \ (t\)” style="vertical-align:middle; "> | \ (x (t)\)” style="vertical-align:middle; "> | \ (y (t)\)” style="vertical-align:middle; "> |
La gráfica de esta curva plana aparece en la siguiente gráfica.
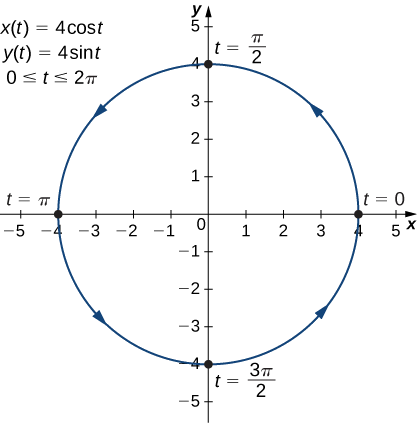
Esta es la gráfica de un círculo con radio\(4\) centrado en el origen, con una orientación en sentido antihorario. Tanto el punto inicial como el punto final de la curva tienen coordenadas\((4,0)\).
Dibuje la curva descrita por las ecuaciones paramétricas
\[ x(t)=3t+2,\quad y(t)=t^2−1,\quad \text{for }−3≤t≤2. \nonumber \]
- Pista
-
Hacer una tabla de valores para\(x(t)\) y\(y(t)\) usando\(t\) valores de\(−3\) a\(2\).
- Contestar
-
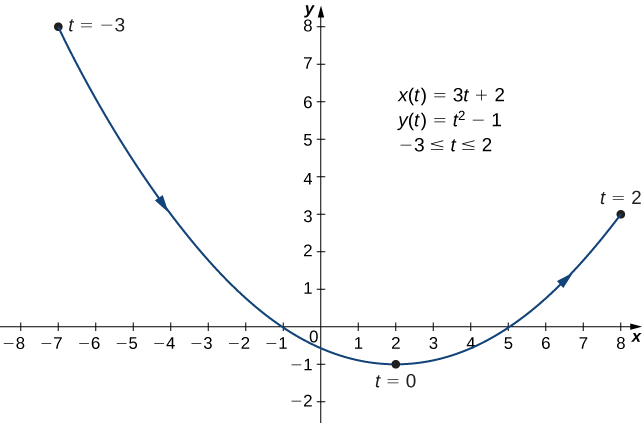
Eliminando el parámetro
Para entender mejor la gráfica de una curva representada paramétricamente, es útil reescribir las dos ecuaciones como una sola ecuación relacionando las variables\(x\) y\(y\). Entonces podemos aplicar cualquier conocimiento previo de ecuaciones de curvas en el plano para identificar la curva. Por ejemplo, las ecuaciones que describen la curva plana en Ejemplo\(\PageIndex{1b}\) son
\[\begin{align} x(t) &=t^2−3 \label{x1} \\[4pt] y(t) &=2t+1 \label{y1} \end{align} \]
sobre la región\(-2 \le t \le 3.\)
Resolviendo Ecuación\ ref {y1} para\(t\) da
\[t=\dfrac{y−1}{2}. \nonumber \]
Esto se puede sustituir en la Ecuación\ ref {x1}:
\[\begin{align} x &=\left(\dfrac{y−1}{2}\right)^2−3 \\[4pt] &=\dfrac{y^2−2y+1}{4}−3 \\[4pt] &=\dfrac{y^2−2y−11}{4}. \label{y2}\end{align} \]
La ecuación\ ref {y2} describe\(x\) como una función de\(y\). Estos pasos dan un ejemplo de eliminación del parámetro. La gráfica de esta función es una parábola que se abre a la derecha (Figura\(\PageIndex{4}\)). Recordemos que la curva plana comenzó en\((1,−3)\) y terminó en\((6,7)\). Estas terminaciones se debieron a la restricción del parámetro\(t\).
Elimine el parámetro para cada una de las curvas de plano descritas por las siguientes ecuaciones paramétricas y describa la gráfica resultante.
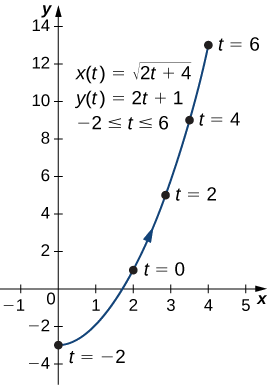
- \(x(t)=\sqrt{2t+4}, \quad y(t)=2t+1,\quad \text{for }−2≤t≤6\)
- \(x(t)=4\cos t, \quad y(t)=3\sin t,\quad \text{for }0≤t≤2π\)
Solución
a. para eliminar el parámetro, podemos resolver cualquiera de las ecuaciones para\(t\). Por ejemplo, resolver la primera ecuación para\(t\) da
\[\begin{align*} x &=\sqrt{2t+4} \\[4pt] x^2 &=2t+4 \\[4pt] x^2−4 &=2t \\[4pt] t &=\dfrac{x^2−4}{2}. \end{align*}\]
Tenga en cuenta que cuando cuadramos ambos lados es importante observar eso\(x≥0\). Sustituir\(t=\dfrac{x^2−4}{2}\) en\(y(t)\) rendimientos
\[ y(t)=2t+1 \nonumber \]
\[ y=2\left(\dfrac{x^2−4}{2}\right)+1 \nonumber \]
\[ y=x^2−4+1 \nonumber \]
\[ y=x^2−3. \nonumber \]
Esta es la ecuación de una parábola que se abre hacia arriba. Sin embargo, existe una restricción de dominio debido a los límites del parámetro\(t\). Cuando\(t=−2\),\(x=\sqrt{2(−2)+4}=0\), y cuando\(t=6\),\(x=\sqrt{2(6)+4}=4\). Sigue la gráfica de esta curva plana.
b. A veces es necesario ser un poco creativo en la eliminación del parámetro. Las ecuaciones paramétricas para este ejemplo son
\[ x(t)=4 \cos t\nonumber \]
y
\[ y(t)=3 \sin t\nonumber \]
Resolver cualquiera de las dos ecuaciones para\(t\) directamente no es aconsejable porque seno y coseno no son funciones uno a uno. Sin embargo, dividir la primera ecuación por\(4\) y la segunda ecuación por\(3\) (y suprimir la\(t\)) nos da
\[ \cos t=\dfrac{x}{4}\nonumber \]
y
\[ \sin t=\dfrac{y}{3}.\nonumber \]
Ahora usa la identidad pitagórica\(\cos^2t+\sin^2t=1\) y reemplaza las expresiones por\(\sin t\) y\(\cos t\) por las expresiones equivalentes en términos de\(x\) y\(y\). Esto da
\[ \left(\dfrac{x}{4}\right)^2+\left(\dfrac{y}{3}\right)^2=1 \nonumber \]
\[ \dfrac{x^2}{16}+\dfrac{y^2}{9}=1. \nonumber \]
Esta es la ecuación de una elipse horizontal centrada en el origen, con semieje mayor\(4\) y semieje menor\(3\) como se muestra en la siguiente gráfica.
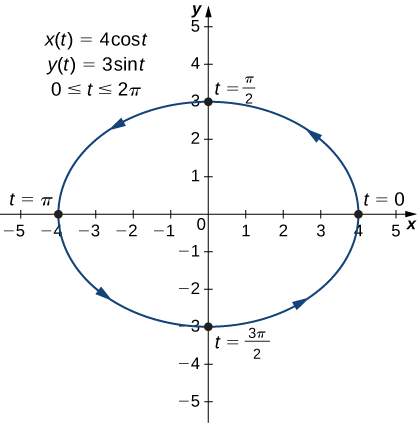
A medida que t avanza de\(0\) a\(2π\), un punto en la curva atraviesa la elipse una vez, en sentido contrario a las agujas del reloj. Recordemos del abridor de sección que la órbita de la Tierra alrededor del Sol también es elíptica. Este es un ejemplo perfecto del uso de curvas parametrizadas para modelar un fenómeno del mundo real.
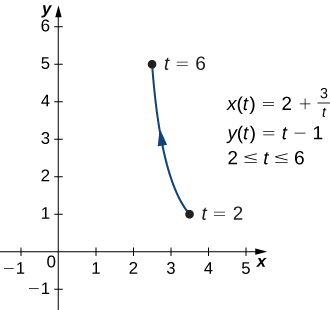
Elimine el parámetro para la curva plana definida por las siguientes ecuaciones paramétricas y describa la gráfica resultante.
\[ x(t)=2+\dfrac{3}{t}, \quad y(t)=t−1, \quad\text{for }2≤t≤6 \nonumber \]
- Pista
-
Resolver una de las ecuaciones\(t\) y sustituirla en la otra ecuación.
- Contestar
-
\(x=2+\frac{3}{y+1},\)o\(y=−1+\frac{3}{x−2}\). Esta ecuación describe una porción de una hipérbola rectangular centrada en\((2,−1)\).
Hasta el momento hemos visto el método de eliminar el parámetro, suponiendo que conocemos un conjunto de ecuaciones paramétricas que describen una curva plana. ¿Y si quisiéramos comenzar con la ecuación de una curva y determinar un par de ecuaciones paramétricas para esa curva? Esto es ciertamente posible, y de hecho es posible hacerlo de muchas maneras diferentes para una curva dada. El proceso se conoce como parametrización de una curva.
Encuentra dos pares diferentes de ecuaciones paramétricas para representar la gráfica de\(y=2x^2−3\).
Solución
Primero, siempre es posible parametrizar una curva definiendo\(x(t)=t\), luego reemplazando\(x\) con\(t\) en la ecuación para\(y(t)\). Esto da la parametrización
\[ x(t)=t, \quad y(t)=2t^2−3. \nonumber \]
Dado que no hay restricción sobre el dominio en la gráfica original, no hay restricción en los valores de\(t\).
Tenemos total libertad en la elección de la segunda parametrización. Por ejemplo, podemos elegir\(x(t)=3t−2\). Lo único que debemos verificar es que no se impongan restricciones\(x\); es decir, el rango de\(x(t)\) es todo números reales. Este es el caso de\(x(t)=3t−2\). Ahora desde\(y=2x^2−3\), podemos\(x(t)=3t−2\) sustituir\(x\). Esto da
\[ y(t)=2(3t−2)^2−2=2(9t^2−12t+4)−2=18t^2−24t+8−2=18t^2−24t+6. \nonumber \]
Por lo tanto, una segunda parametrización de la curva se puede escribir como
\( x(t)=3t−2\)y\( y(t)=18t^2−24t+6.\)
Encuentra dos conjuntos diferentes de ecuaciones paramétricas para representar la gráfica de\(y=x^2+2x\).
- Pista
-
Siga los pasos en Ejemplo\(\PageIndex{3}\). Recuerda que tenemos libertad en elegir la parametrización para\(x(t)\).
- Contestar
-
Una posibilidad es\(x(t)=t, \quad y(t)=t^2+2t.\) Otra posibilidad es\(x(t)=2t−3, \quad y(t)=(2t−3)^2+2(2t−3)=4t^2−8t+3.\) Hay, de hecho, un número infinito de posibilidades.
Cicloides y otras curvas paramétricas
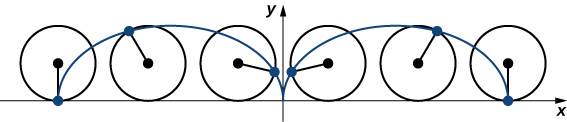
Imagínese ir a dar un paseo en bicicleta por el país. Las llantas permanecen en contacto con la carretera y giran en un patrón predecible. Ahora supongamos que una hormiga muy decidida está cansada después de un largo día y quiere llegar a casa. Por lo que se cuelga del costado de la llanta y obtiene un paseo gratis. El camino que recorre esta hormiga por un camino recto se denomina cicloide (Figura\( \PageIndex{8}\)). Un cicloide generado por un círculo (o rueda de bicicleta) de radio a viene dado por las ecuaciones paramétricas
\[x(t)=a(t−\sin t), \quad y(t)=a(1−\cos t).\nonumber \]
Para ver por qué esto es cierto, considera el camino que toma el centro de la rueda. El centro se mueve a lo largo del\(x\) eje a una altura constante igual al radio de la rueda. Si el radio es\(a\), entonces las coordenadas del centro pueden ser dadas por las ecuaciones
\[x(t)=at,\quad y(t)=a\nonumber \]
por cualquier valor de\(t\). A continuación, considere la hormiga, que gira alrededor del centro a lo largo de un camino circular. Si la bicicleta se mueve de izquierda a derecha entonces las ruedas giran en sentido horario. Una posible parametrización del movimiento circular de la hormiga (relativo al centro de la rueda) viene dada por
\[\begin{align*} x(t) &=−a \sin t \\[4pt] y(t) &=−a\cos t.\end{align*}\]
(El signo negativo es necesario para invertir la orientación de la curva. Si el signo negativo no estuviera ahí, tendríamos que imaginar la rueda girando en sentido antihorario.) Al sumar estas ecuaciones se obtienen las ecuaciones para el cicloide.
\[\begin{align*} x(t) &=a(t−\sin t) \\[4pt] y(t) &=a(1−\cos t ) \end{align*}\]
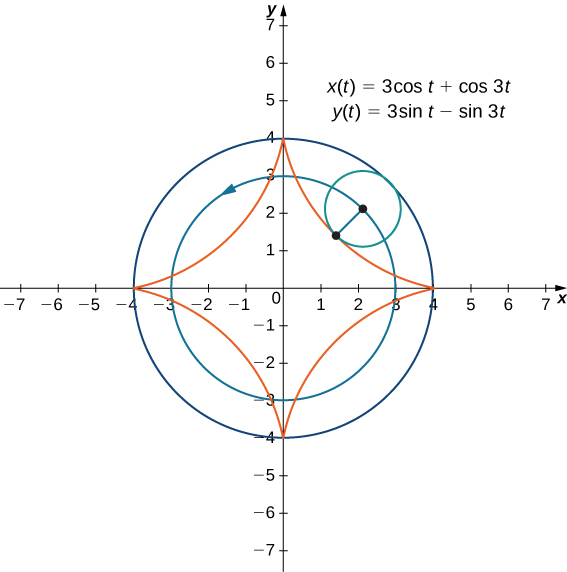
Ahora supongamos que la rueda de la bicicleta no recorre una carretera recta sino que se mueve por el interior de una rueda más grande, como en la Figura\( \PageIndex{9}\). En esta gráfica, el círculo verde se desplaza alrededor del círculo azul en sentido contrario a las agujas del reloj. Un punto en el borde del círculo verde traza la gráfica roja, que se llama hipocicloide.
Las ecuaciones paramétricas generales para un hipocicloide son
\[x(t)=(a−b) \cos t+b \cos (\dfrac{a−b}{b})t \nonumber \]
\[y(t)=(a−b) \sin t−b \sin (\dfrac{a−b}{b})t. \nonumber \]
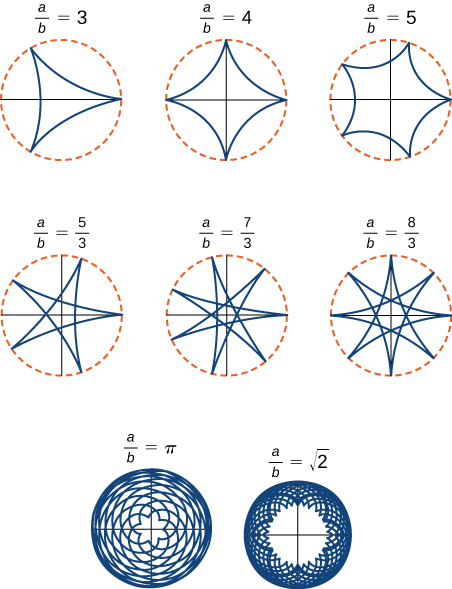
Estas ecuaciones son un poco más complicadas, pero la derivación es algo similar a las ecuaciones para el cicloide. En este caso suponemos que el radio del círculo más grande es\(a\) y el radio del círculo más pequeño es\(b\). Entonces el centro de la rueda viaja a lo largo de un círculo de radio\(a−b.\) Este hecho explica el primer término en cada ecuación anterior. El periodo de la segunda función trigonométrica en ambos\(x(t)\) y\(y(t)\) es igual a\(\dfrac{2πb}{a−b}\).
La relación\(\dfrac{a}{b}\) se relaciona con el número de cúspides en la gráfica (las cúspides son las esquinas o extremos puntiagudos de la gráfica), como se ilustra en la Figura\( \PageIndex{10}\). Esta relación puede llevar a algunas gráficas muy interesantes, dependiendo de si la relación es racional o no. La figura\(\PageIndex{9}\) corresponde a\(a=4\) y\(b=1\). El resultado es un hipocicloide con cuatro cúspides. La figura\(\PageIndex{10}\) muestra algunas otras posibilidades. Los dos últimos hipocicloides tienen valores irracionales para\(\dfrac{a}{b}\). En estos casos los hipocicloides tienen un número infinito de cúspides, por lo que nunca regresan a su punto de partida. Estos son ejemplos de lo que se conoce como curvas de relleno de espacio.
Muchas curvas planas en matemáticas llevan el nombre de las personas que primero las investigaron, como el folium de Descartes o la espiral de Arquímedes. No obstante, quizás el nombre más extraño para una curva es la bruja de Agnesi. ¿Por qué una bruja?
Maria Gaetana Agnesi (1718—1799) fue una de las pocas matemáticas reconocidas de la Italia del siglo XVIII. Escribió un popular libro sobre geometría analítica, publicado en 1748, que incluía una interesante curva que había sido estudiada por Fermat en 1630. El matemático Guido Grandi mostró en 1703 cómo construir esta curva, a la que más tarde llamó la “versoria”, término latino para una cuerda utilizada en la navegación. Agnesi usó el término italiano para esta cuerda, “versiera”, pero en latín, esta misma palabra significa un “duende femenino”. Cuando el libro de Agnesi fue traducido al inglés en 1801, el traductor utilizó el término “bruja” para la curva, en lugar de cuerda. El nombre de “bruja de Agnesi” se ha quedado atascado desde entonces.
La bruja de Agnesi es una curva definida de la siguiente manera: Comience con un círculo de radio a de manera que los puntos\((0,0)\) y\((0,2a)\) sean puntos en el círculo (Figura\( \PageIndex{11}\)). Que O denote el origen. Elija cualquier otro punto A en el círculo y dibuje la línea secante OA. Deje que B denote el punto en el que la línea OA cruza la línea horizontal a través de\((0,2a)\). La línea vertical a través de B cruza la línea horizontal a través de A en el punto P. A medida que el punto A varía, la trayectoria que recorre el punto P es la curva bruja de Agnesi para el círculo dado.
Las curvas de Witch of Agnesi tienen aplicaciones en física, incluyendo el modelado de ondas de agua y distribuciones de líneas espectrales. En teoría de probabilidad, la curva describe la función de densidad de probabilidad de la distribución de Cauchy. En este proyecto parametrizarás estas curvas.
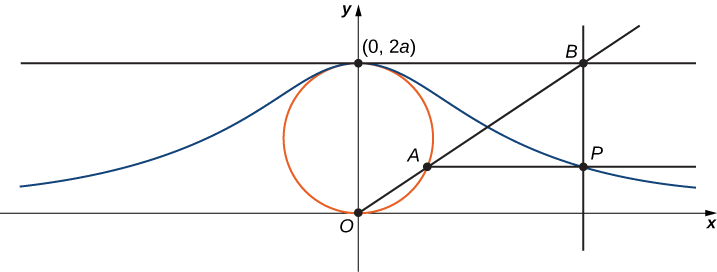
1. En la figura, etiquete los siguientes puntos, longitudes y ángulos:
a.\(C\) es el punto en el\(x\) eje con la misma\(x\) coordenada que\(A\).
b.\(x\) es la\(x\) coordenada de\(P\), y\(y\) es la\(y\) coordenada de\(P\).
c.\(E\) es el punto\((0,a)\).
d.\(F\) es el punto en el segmento de línea\(OA\) tal que el segmento de línea\(EF\) es perpendicular al segmento de línea\(OA\).
e.\(b\) es la distancia de\(O\) a\(F\).
f.\(c\) es la distancia de\(F\) a\(A\).
g.\(d\) es la distancia de\(O\) a\(C\).
h.\(θ\) es la medida del ángulo\(∠COA\).
El objetivo de este proyecto es parametrizar a la bruja usando\(θ\) como parámetro. Para ello, escribe ecuaciones para\(x\) y\(y\) en términos de solo\(θ\).
2. \(d=\dfrac{2a}{\sin θ}\)Demuéstralo.
3. Tenga en cuenta que\(x=d\cos θ\). \(x=2a\cot θ\)Demuéstralo. Al hacer esto, habrás parametrizado la\(x\) coordenada -de la curva con respecto a\(θ\). Si puedes obtener una ecuación similar para\(y\), habrás parametrizado la curva.
4. En términos de\(θ\), ¿cuál es el ángulo\(∠EOA\)?
5. \(b+c=2a\cos\left(\frac{π}{2}−θ\right)\)Demuéstralo.
6. \(y=2a\cos\left(\frac{π}{2}−θ\right)\sin θ\)Demuéstralo.
7. \(y=2a\sin^2θ\)Demuéstralo. Ahora ha parametrizado la\(y\) coordenada -de la curva con respecto a\(θ\).
8. Concluir que una parametrización de la curva de bruja dada es
\[x=2a\cot θ, \quad y=2a \sin^2θ, \quad\text{for }−∞<θ<∞. \nonumber \]
9. Usa tu parametrización para mostrar que la curva de bruja dada es la gráfica de la función\(f(x)=\dfrac{8a^3}{x^2+4a^2}\).
Anteriormente en esta sección, observamos las ecuaciones paramétricas para un cicloide, que es la trayectoria que un punto en el borde de una rueda traza a medida que la rueda rueda a lo largo de una trayectoria recta. En este proyecto observamos dos variaciones diferentes del cicloide, llamadas cicloides curtate y prolate.
Primero, revisemos la derivación de las ecuaciones paramétricas para un cicloide. Recordemos que consideramos una hormiga tenaz tratando de llegar a casa colgándose del borde de una llanta de bicicleta. Hemos asumido que la hormiga se subió al neumático en el mismo borde, donde el neumático toca el suelo. A medida que rueda la rueda, la hormiga se mueve con el borde de la llanta (Figura\(\PageIndex{12}\)).
Como hemos comentado, tenemos mucha flexibilidad a la hora de parametrizar una curva. En este caso dejamos que nuestro parámetro t represente el ángulo por el que ha girado el neumático. Mirando Figura\( \PageIndex{12}\), vemos que después de que el neumático ha girado a través de un ángulo de\(t\), la posición del centro de la rueda,\(C=(x_C,y_C)\), viene dada por
\(x_C=at\)y\(y_C=a\).
Además, dejando\(A=(x_A,y_A)\) denotar la posición de la hormiga, observamos que
\(x_C−x_A=a\sin t\)y\(y_C−y_A=a \cos t\)
Entonces
\[x_A=x_C−a\sin t=at−a\sin t=a(t−\sin t) \nonumber \]
\[y_A=y_C−a\cos t=a−a\cos t=a(1−\cos t). \nonumber \]
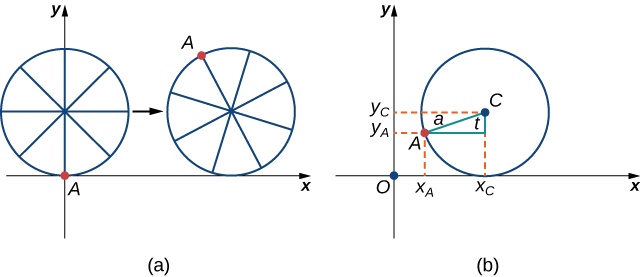
Tenga en cuenta que estas son las mismas representaciones paramétricas que teníamos antes, pero ahora hemos asignado un significado físico a la variable paramétrica\(t\).
Después de un tiempo la hormiga se está mareando por dar vueltas y vueltas en el borde de la llanta. Por lo que sube uno de los radios hacia el centro de la rueda. Al subir hacia el centro de la rueda, la hormiga ha cambiado su trayectoria de movimiento. El nuevo camino tiene menos movimiento hacia arriba y hacia abajo y se llama cicloide curtate (Figura\( \PageIndex{13}\)). Como se muestra en la figura, dejamos que b denote la distancia a lo largo del radio desde el centro de la rueda hasta la hormiga. Como antes, dejamos que t represente el ángulo por el que ha girado el neumático. Adicionalmente, dejamos\(C=(x_C,y_C)\) representar la posición del centro de la rueda y\(A=(x_A,y_A)\) representar la posición de la hormiga.
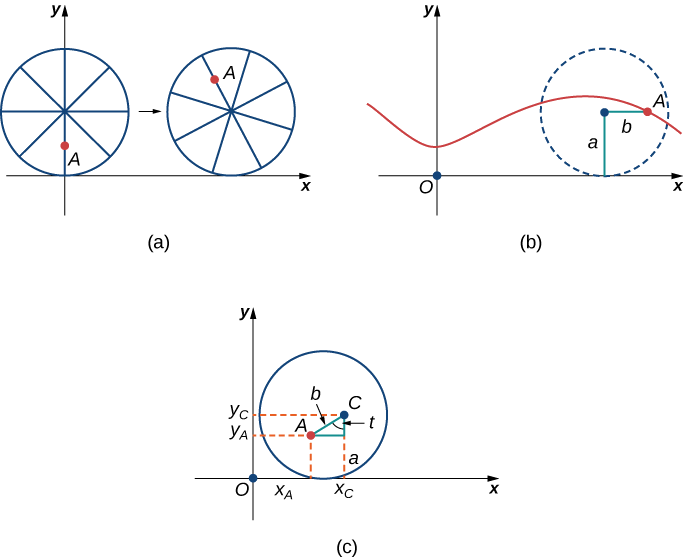
1. ¿Cuál es la posición del centro de la rueda después de que la llanta haya girado en un ángulo de\(t\)?
2. Utilice la geometría para buscar expresiones para\(x_C−x_A\) y para\(y_C−y_A\).
3. A partir de sus respuestas a las partes 1 y 2, ¿cuáles son las ecuaciones paramétricas que representan el cicloide curtate?
Una vez que la cabeza de la hormiga se aclara, se da cuenta de que el ciclista ha dado un giro, y ahora viaja lejos de su casa. Por lo que deja caer la llanta de la bicicleta y mira a su alrededor. Afortunadamente, hay un conjunto de vías de tren cerca, que se dirigen de nuevo en la dirección correcta. Entonces la hormiga se dirige a las vías del tren para esperar. Después de un rato, pasa un tren, yendo en la dirección correcta, y logra saltar y simplemente coger el borde de la rueda del tren (¡sin ser aplastado!).
A la hormiga le sigue preocupando marearse, pero la rueda del tren está resbaladiza y no tiene radios para escalar, por lo que decide simplemente agarrarse al borde de la rueda y esperar lo mejor. Ahora, las ruedas del tren tienen una brida para mantener la rueda funcionando en las vías. Entonces, en este caso, dado que la hormiga está colgando del mismo borde de la brida, la distancia desde el centro de la rueda a la hormiga es en realidad mayor que el radio de la rueda (Figura\(\PageIndex{14}\)).
La configuración aquí es esencialmente la misma que cuando la hormiga subió el radio en la rueda de la bicicleta. Dejamos que b denote la distancia desde el centro de la rueda hasta la hormiga, y dejamos que t represente el ángulo por el que ha girado el neumático. Adicionalmente, dejamos\(C=(x_C,y_C)\) representar la posición del centro de la rueda y\(A=(x_A,y_A)\) representar la posición de la hormiga (Figura\( \PageIndex{14}\)).
Cuando la distancia desde el centro de la rueda a la hormiga es mayor que el radio de la rueda, su trayectoria de movimiento se denomina cicloide prolado. En la figura se muestra una gráfica de un cicloide prolado.
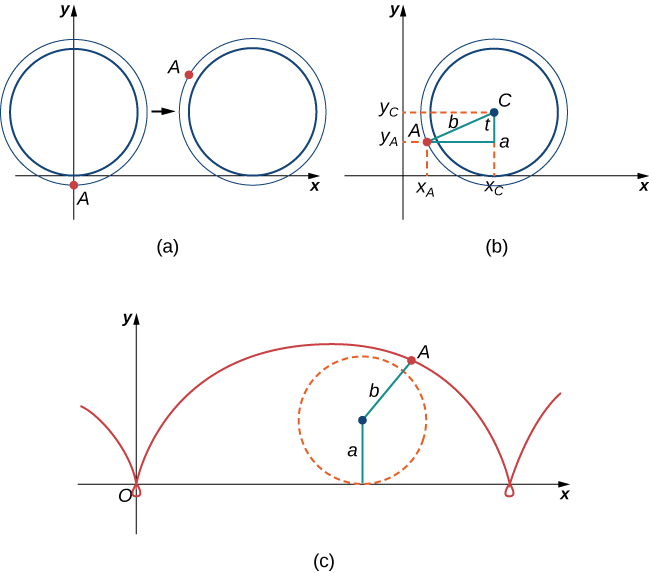
4. Usando el mismo enfoque que utilizó en las partes 1— 3, encuentre las ecuaciones paramétricas para la trayectoria de movimiento de la hormiga.
5. ¿Qué notas sobre tu respuesta a la parte 3 y tu respuesta a la parte 4?
Observe que la hormiga en realidad está viajando hacia atrás por momentos (los “bucles” en la gráfica), aunque el tren siga avanzando. ¡Probablemente va a estar muy mareado para cuando llegue a casa!
Conceptos clave
- Las ecuaciones paramétricas proporcionan una manera conveniente de describir una curva. Un parámetro puede representar el tiempo o alguna otra cantidad significativa.
- A menudo es posible eliminar el parámetro en una curva parametrizada para obtener una función o relación que describa esa curva.
- Siempre hay más de una forma de parametrizar una curva.
- Las ecuaciones paramétricas pueden describir curvas complicadas que son difíciles o quizás imposibles de describir usando coordenadas rectangulares.
Glosario
- cicloide
- la curva trazada por un punto en la llanta de una rueda circular a medida que la rueda rueda a lo largo de una línea recta sin deslizamiento
- cúspide
- un extremo puntiagudo o parte donde dos curvas se encuentran
- orientación
- la dirección que un punto se mueve en una gráfica a medida que aumenta el parámetro
- parámetro
- una variable independiente que tanto\(x\) y\(y\) depende en una curva paramétrica; generalmente representada por la variable\(t\)
- curva paramétrica
- la gráfica de las ecuaciones paramétricas\(x(t)\) y\(y(t)\) sobre un intervalo\(a≤t≤b\) combinado con las ecuaciones
- ecuaciones paramétricas
- las ecuaciones\(x=x(t)\) y\(y=y(t)\) que definen una curva paramétrica
- parametrización de una curva
- reescribir la ecuación de una curva definida por una función\(y=f(x)\) como ecuaciones paramétricas


