16.5: Divergencia y Curl
- Page ID
- 116728
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Determinar la divergencia a partir de la fórmula para un campo vectorial dado.
- Determine curl a partir de la fórmula para un campo vectorial dado.
- Utilice las propiedades de curl y divergencia para determinar si un campo vectorial es conservador.
En esta sección, examinamos dos operaciones importantes en un campo vectorial: divergencia y curl. Son importantes para el campo del cálculo por varias razones, entre ellas el uso del rizo y la divergencia para desarrollar algunas versiones de dimensiones superiores del Teorema Fundamental del Cálculo. Además, el rizo y la divergencia aparecen en las descripciones matemáticas de la mecánica de fluidos, el electromagnetismo y la teoría de la elasticidad, que son conceptos importantes en física e ingeniería. También podemos aplicar rizo y divergencia a otros conceptos que ya exploramos. Por ejemplo, bajo ciertas condiciones, un campo vectorial es conservador si y solo si su rizo es cero.
Además de definir el rizo y la divergencia, observamos algunas interpretaciones físicas de las mismas y mostramos su relación con campos vectoriales conservadores y libres de fuentes.
Divergencia
La divergencia es una operación en un campo vectorial que nos dice cómo se comporta el campo hacia o lejos de un punto. Localmente, la divergencia de un campo vectorial\(\vecs{F}\)\(\mathbb{R}^3\) en\(\mathbb{R}^2\) o en un punto particular\(P\) es una medida del “flujo de salida” del campo vectorial en\(P\). Si\(\vecs{F}\) representa la velocidad de un fluido, entonces la divergencia de\(\vecs{F}\) at\(P\) mide la tasa neta de cambio con respecto al tiempo de la cantidad de fluido que fluye lejos\(P\) (la tendencia del fluido a fluir “fuera de” P). En particular, si la cantidad de fluido que fluye hacia adentro\(P\) es la misma que la cantidad que fluye hacia afuera, entonces la divergencia a\(P\) es cero.
Si\(\vecs{F} = \langle P,Q,R \rangle\) es un campo vectorial en\(\mathbb{R}^3\) y\(P_x, \, Q_y, \) y\(R_z\) todos existen, entonces la divergencia de\(\vecs{F}\) se define por
\[\begin{align} \text{div}\, F &= P_x + Q_y + R_z \\[4pt] &= \dfrac{\partial P}{\partial x} + \dfrac{\partial Q}{\partial y} + \dfrac{\partial R}{\partial z}. \end{align} \nonumber \]
Tenga en cuenta que la divergencia de un campo vectorial no es un campo vectorial, sino una función escalar. En términos del operador de gradiente
\[\vecs \nabla = \langle \dfrac{\partial}{\partial x}, \dfrac{\partial}{\partial y}, \dfrac{\partial}{\partial z} \rangle \nonumber \]
la divergencia se puede escribir simbólicamente como el producto de punto
\[\text{div}\, \vecs F = \vecs \nabla \cdot \vecs{F}. \nonumber \]
Tenga en cuenta que esto es meramente una notación útil, porque el producto punto de un vector de operadores y un vector de funciones no está definido de manera significativa dada nuestra definición actual de producto de punto.
Si\(\vecs{F} = \langle P,Q \rangle\) es un campo vectorial en\(\mathbb{R}^2\),\(P_x\) y\(Q_y\) ambos existen, entonces la divergencia de\(\vecs{F}\) se define de manera similar como
\[\begin{align*} \text{div}\, \vecs{F} &= P_x + Q_y \\[4pt] &= \dfrac{\partial P}{\partial x} + \dfrac{\partial Q}{\partial y} \\[4pt] &= \vecs \nabla \cdot \vecs{F}. \end{align*}\]
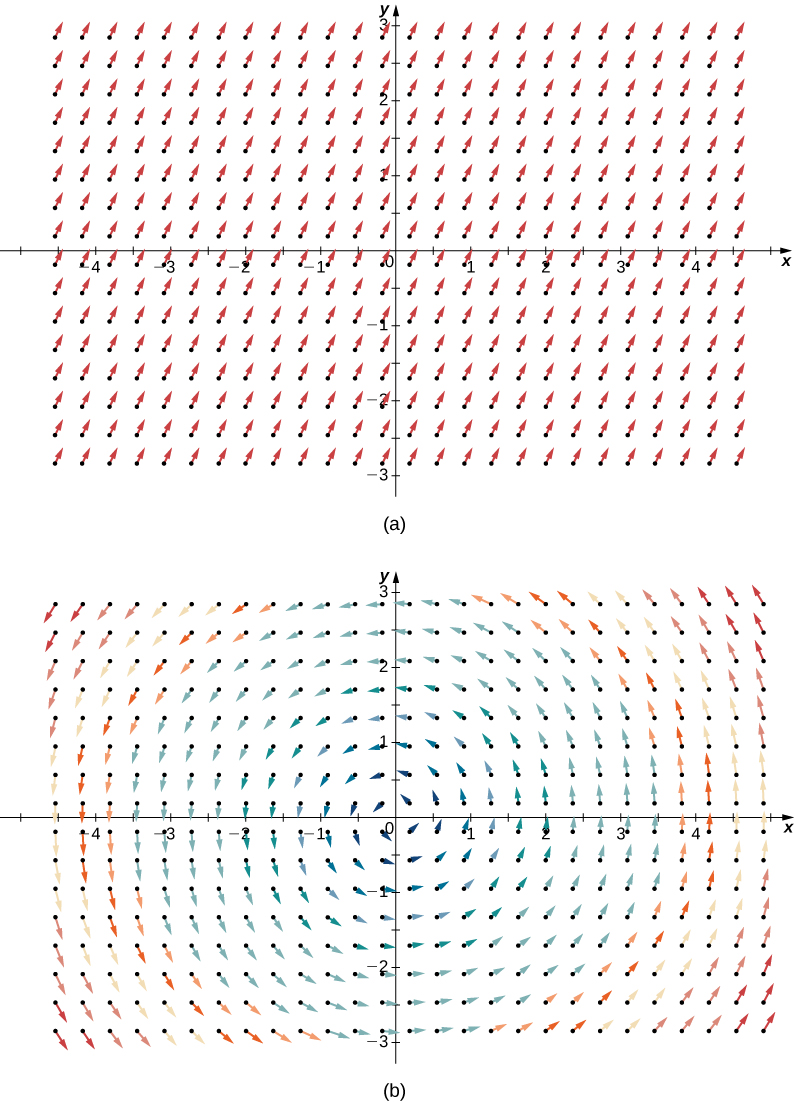
Para ilustrar este punto, considere los dos campos vectoriales en la Figura\(\PageIndex{1}\). En cualquier punto en particular, la cantidad que fluye adentro es la misma que la cantidad que fluye hacia afuera, por lo que en cada punto la “salida” del campo es cero. Por lo tanto, esperamos que la divergencia de ambos campos sea cero, y esto es efectivamente el caso, ya que
\[\text{div}(\langle 1,2 \rangle ) = \dfrac{\partial}{\partial x} (1) + \dfrac{\partial}{\partial y}(2) = 0 \nonumber \]
y
\[\text{div}(\langle -y,x \rangle ) = \dfrac{\partial}{\partial x} (-y) + \dfrac{\partial}{\partial y} (x) = 0. \nonumber \]
Por el contrario, considere el campo vectorial radial\(\vecs{R} (x,y) = \langle -x, -y \rangle\) en la Figura\(\PageIndex{2}\). En cualquier punto dado, fluye más fluido que fluye hacia afuera, y por lo tanto la “salida” del campo es negativa. Esperamos que la divergencia de este campo sea negativa, y esto es efectivamente el caso, ya que
\[\text{div}(\vecs{R}) = \dfrac{\partial}{\partial x} (-x) + \dfrac{\partial}{\partial y} (-y) = -2. \nonumber \]
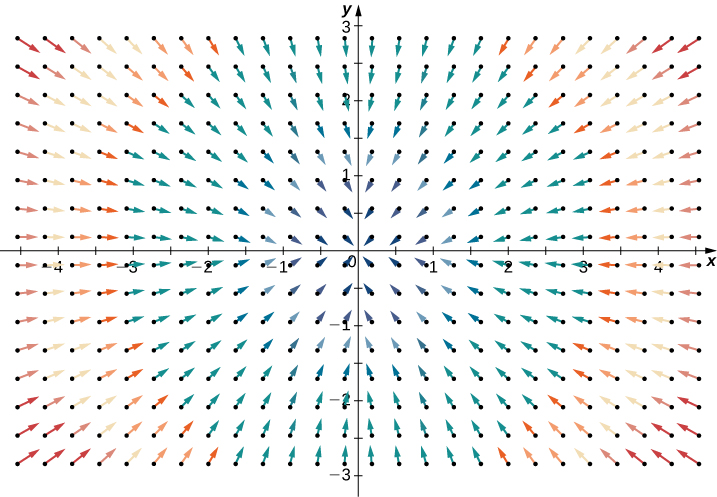
Para tener una idea global de lo que nos está diciendo la divergencia, supongamos que un campo vectorial en\(\mathbb{R}^2\) representa la velocidad de un fluido. Imagina tomar un círculo elástico (un círculo con una forma que puede ser cambiada por el campo vectorial) y dejándolo caer en un fluido. Si el círculo mantiene su área exacta a medida que fluye a través del fluido, entonces la divergencia es cero. Esto ocurriría para ambos campos vectoriales en la Figura\(\PageIndex{1}\). Por otro lado, si la forma del círculo se distorsiona para que su área se encoja o se expanda, entonces la divergencia no es cero. Imagínese caer tal círculo elástico en el campo vectorial radial en la Figura\(\PageIndex{2}\) para que el centro del círculo aterrice en el punto\((3, 3)\). El círculo fluiría hacia el origen, y al hacerlo el frente del círculo viajaría más despacio que el trasero, provocando que el círculo se “arremolcara” y perdiera área. Es así como se puede ver una divergencia negativa.
Si\(\vecs{F}(x,y,z) = e^x \hat{i} + yz \hat{j} - yz^2 \hat{k}\), entonces encuentra la divergencia de\(\vecs{F}\) at\((0,2,-1)\).
Solución
La divergencia de\(\vecs{F}\) es
\[\dfrac{\partial}{\partial x} (e^x) + \dfrac{\partial}{\partial y}(yz) - \dfrac{\partial}{\partial z} (y z^2) = e^x + z - 2yz. \nonumber \]
Por lo tanto, la divergencia en\((0,2,-1)\) es\(e^0 - 1 + 4 = 4\). Si\(\vecs{F}\) representa la velocidad de un fluido, entonces fluye más fluido que fluyendo hacia adentro en el punto\((0,2,-1)\).
Buscar\(\text{div}\, \vecs{F}\) para
\[\vecs{F}(x,y,z) = \langle xy, \, 5-z^2, \, x^2 + y^2 \rangle \nonumber. \nonumber \]
- Pista
-
Seguir Ejemplo\(\PageIndex{1}\).
- Contestar
-
\(\text{div}\, \vecs{F} = y \)
Otra aplicación para la divergencia es detectar si un campo está libre de fuente. Recordemos que un campo libre de fuente es un campo vectorial que tiene una función de flujo; equivalentemente, un campo libre de fuente es un campo con un flujo que es cero a lo largo de cualquier curva cerrada. Los dos teoremas siguientes dicen que, bajo ciertas condiciones, los campos vectoriales libres de fuente son precisamente los campos vectoriales con divergencia cero.
Si\(\vecs{F} = \langle P,Q \rangle\) es un campo vectorial continuo sin fuente con funciones de componentes diferenciables, entonces\(\text{div}\, \vecs{F} = 0\).
Ya que\(\vecs{F}\) es fuente libre, hay una función\(g(x,y)\) con\(g_y = P\) y\(-g_x = Q\). Por lo tanto,\(\vecs{F} = \langle g_y, -g_x \rangle\) y\(\text{div}\, \vecs{F} = g_{yx} - g_{xy} = 0\) por el teorema de Clairaut.
\(\square\)
Lo contrario de Divergencia de un Campo Vector Libre de Fuente es cierto en regiones simplemente conectadas, pero la prueba es demasiado técnica para incluirla aquí. Así, tenemos el siguiente teorema, que puede probar si un campo vectorial en\(\mathbb{R}^2\) es libre de fuente.
Let\(\vecs{F} = \langle P,Q \rangle \) Ser un campo vectorial continuo con funciones componentes diferenciables con un dominio que simplemente está conectado. Entonces,\(\text{div}\, \vecs{F} = 0\) si y sólo si\(\vecs{F}\) es fuente libre.
¿La\(\vecs{F} (x,y) = \langle x^2 y, \, 5 - xy^2 \rangle\) fuente de campo es gratuita?
Solución
Tenga en cuenta el dominio de\(\vecs{F}\) es\(\mathbb{R}^2\) el que simplemente está conectado. Además,\(\vecs{F}\) es continuo con funciones de componentes diferenciables. Por lo tanto, podemos usar la prueba de divergencia para campos vectoriales libres de fuente para analizar\(\vecs{F}\). La divergencia de\(\vecs{F}\) es
\[\dfrac{\partial}{\partial x} (x^2 y) + \dfrac{\partial}{\partial y} (5 - xy^2 ) = 2xy - 2xy = 0. \nonumber \]
Por lo tanto,\(\vecs{F}\) es fuente libre por la prueba de divergencia para campos vectoriales libres de fuente.
Dejar\(\vecs{F} (x,y) = \langle -ay, bx \rangle\) ser un campo rotacional donde\(a\) y\(b\) son constantes positivas. ¿La\(\vecs{F}\) fuente es gratuita?
- Pista
-
Calcular la divergencia.
- Contestar
-
Sí
Recordemos que la forma de flujo del teorema de Green dice que
\[\oint_C \vecs F \cdot \vecs N \; ds = \iint_D P_x + Q_y \;dA, \nonumber \]
donde\(C\) es una curva cerrada simple y\(D\) es la región encerrada por\(C\). Ya que\(P_x + Q_y = \text{div}\,\vecs F\), el teorema de Green a veces se escribe como
\[\oint_C \vecs F \cdot \vecs N\; ds = \iint_D \text{div}\, \vecs F \;dA. \nonumber \]
Por lo tanto, el teorema de Green puede escribirse en términos de divergencia. Si pensamos en la divergencia como una especie de derivado, entonces el teorema de Green dice que el “derivado” de\(\vecs{F}\) en una región puede traducirse en una línea integral de\(\vecs{F}\) a lo largo del límite de la región. Esto es análogo al Teorema Fundamental del Cálculo, en el que la derivada de una función\(f\) en un segmento de línea\([a,b]\) puede traducirse en una declaración\(f\) sobre en el límite de\([a,b]\). Usando la divergencia, podemos ver que el teorema de Green es un análogo de mayor dimensión del Teorema Fundamental del Cálculo.
Podemos utilizar todo lo que hemos aprendido en la aplicación de la divergencia. Let\(\vecs{v}\) Ser un campo vectorial modelando la velocidad de un fluido. Dado que la divergencia de\(\vecs{v}\) en el punto\(P\) mide el “flujo de salida” del fluido en\(P\),\(\text{div}\, v(P) > 0\) implica que fluye más fluido fuera de lo\(P\) que fluye hacia adentro. Del mismo modo,\(\text{div}\, v(P) < 0\) implica\(P\) que cuanto más fluido fluye hacia adentro que fluye hacia afuera, e\(\text{div}\, \vecs{v}(P) = 0\) implica que la misma cantidad de fluido está fluyendo hacia adentro que fluye hacia afuera.
Supongamos que\(\vecs{v}(x,y) = \langle -xy,y \rangle, \, y > 0\) modela el flujo de un fluido. ¿Fluye más fluido hacia el punto\((1,4)\) que fluye hacia afuera?
Solución
Para determinar si fluye más fluido que el\((1,4)\) que fluye hacia afuera, calculamos la divergencia de\(\vecs v\) at\((1,4)\):
\[div(\vecs{v}) = \dfrac{\partial}{\partial x} (-xy) + \dfrac{\partial}{\partial y} (y) = -y + 1. \nonumber \]
Para encontrar la divergencia en\((1,4)\) sustituir el punto en la divergencia:\(-4 + 1 = -3\). Dado que la divergencia de\(\vecs v\) at\((1,4)\) es negativa, fluye más fluido hacia adentro que fluyendo hacia afuera (Figura\(\PageIndex{4}\)).

Para el campo vectorial\(\vecs{v}(x,y) = \langle -xy, y \rangle , \, y > 0\), encuentre todos los puntos de\(P\) tal manera que la cantidad de fluido que fluye hacia adentro\(P\) sea igual a la cantidad de fluido que fluye fuera de\(P\).
- Pista
-
Encuentra donde la divergencia es cero.
- Contestar
-
Todos los puntos en línea\(y = 1\).
Curl
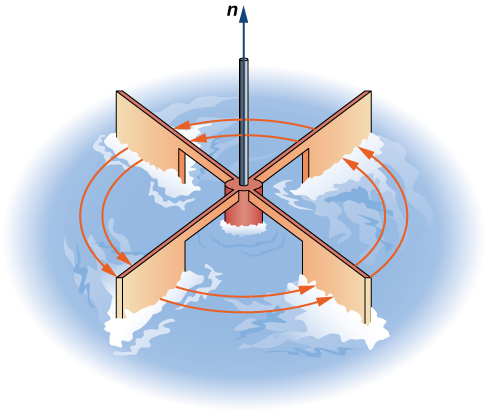
La segunda operación en un campo vectorial que examinamos es el curl, que mide la extensión de rotación del campo alrededor de un punto. Supongamos que\(\vecs{F}\) representa el campo de velocidad de un fluido. Entonces, el rizo de\(\vecs{F}\) at point\(P\) es un vector que mide la tendencia de las partículas cercanas\(P\) a rotar alrededor del eje que apunta en la dirección de este vector. La magnitud del vector curl\(P\) mide la rapidez con la que las partículas giran alrededor de este eje. En otras palabras, el rizo en un punto es una medida del “giro” del campo vectorial en ese punto. Visualmente, imagina colocar una rueda de paletas en un fluido en\(P\), con el eje de la rueda de paletas alineado con el vector de rizo (Figura\(\PageIndex{5}\)). El rizo mide la tendencia de la rueda de paletas a girar.
Considere los campos vectoriales en la Figura\(\PageIndex{1}\). En la parte (a), el campo vectorial es constante y no hay giro en ningún punto. Por lo tanto, esperamos que el rizo del campo sea cero, y este es efectivamente el caso. La parte (b) muestra un campo rotacional, por lo que el campo tiene giro. En particular, si colocas una rueda de paletas en un campo en cualquier punto para que el eje de la rueda sea perpendicular a un plano, la rueda gira en sentido antihorario. Por lo tanto, esperamos que el rizo del campo sea distinto de cero, y este es efectivamente el caso (el rizo es\(2\,\mathbf{\hat k}\)).
Para ver qué rizo mide globalmente, imagina dejar caer una hoja en el fluido. A medida que la hoja se mueve junto con el flujo de fluido, el rizo mide la tendencia de la hoja a girar. Si el rizo es cero, entonces la hoja no gira a medida que se mueve a través del fluido.
Si\(\vecs{F} = \langle P,Q,R \rangle\) es un campo vectorial en\(\mathbb{R}^3\), y\(P_x, \, Q_y\), y\(R_z\) todos existen, entonces el rizo de\(\vecs{F}\) se define por
\ [\ begin {align}\ text {curl}\,\ vecs {F} &= (R_y - Q_z)\,\ mathbf {\ hat i} + (P_z - R_x)\,\ mathbf {\ hat j} + (Q_x - P_y)\,\ mathbf {\ hat k}\\ [4pt]
&=\ left (d\ {\ R parcial} {\ parcial y} -\ dfrac {\ parcial Q} {\ parcial z}\ derecha)\,\ mathbf {\ hat i} +\ izquierda (\ dfrac {\ P parcial} {\ z parcial} -\ dfrac {\ R parcial} {\ x parcial}\ derecha)\,\ mathbf {\ hat j} +\ izquierda (\ dfrac {\ parcial Q} {\ parcial x} -\ dfrac {\ parcial P} {\ parcial y}\ derecha)\,\ mathbf {\ hat k}. \ end {align}\ nonumber\]
Tenga en cuenta que el rizo de un campo vectorial es un campo vectorial, en contraste con la divergencia.
La definición de rizo puede ser difícil de recordar. Para ayudar a recordar, usamos la notación\(\vecs \nabla \times \vecs{F}\) para representar un “determinante” que da la fórmula de curl:
\[\begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ \dfrac{\partial}{\partial x} & \dfrac{\partial}{\partial y} & \dfrac{\partial}{\partial z} \\ P & Q & R \end{vmatrix}. \nonumber \]
El determinante de esta matriz es
\[(R_y - Q_z) \,\mathbf{\hat i} - (R_x - P_z) \,\mathbf{\hat j} + (Q_x - P_y) \,\mathbf{\hat k} = (R_y - Q_z) \,\mathbf{\hat i} + (P_z - R_x) \,\mathbf{\hat j} + (Q_x - P_y)\,\mathbf{\hat k} = \text{curl}\, \vecs{F}. \nonumber \]
Así, esta matriz es una forma de ayudar a recordar la fórmula para el rizo. Tenga en cuenta, sin embargo, que la palabra determinante se usa de manera muy floja. Un determinante no se define realmente en una matriz con entradas que son tres vectores, tres operadores y tres funciones.
Si\(\vecs{F} = \langle P,Q \rangle\) es un campo vectorial en\(\mathbb{R}^2\), entonces el rizo de\(\vecs{F}\), por definición, es
\[\text{curl}\, \vecs{F} = (Q_x - P_y)\,\mathbf{\hat k} = \left(\dfrac{\partial Q}{\partial x} - \dfrac{\partial P}{\partial y} \right)\,\mathbf{\hat k}. \nonumber \]
Encuentra el rizo de\(\vecs{F}(P,Q,R) = \langle x^2 z, e^y + xz, xyz \rangle\).
Solución
El rizo es
\[\begin{align*} \text{curl}\, f &= \vecs\nabla \times \vecs{F} \\ &= \begin{vmatrix} \mathbf{\hat i} & \mathbf{\hat j} & \mathbf{\hat k} \\ \partial/\partial x & \partial/\partial y & \partial / \partial z \\ P & Q & R \end{vmatrix} \\ &= (R_y - Q_z)\,\mathbf{\hat i} + (P_z - R_x)\,\mathbf{\hat j} + (Q_x - P_y)\,\mathbf{\hat k} \\ &= (xz - x)\,\mathbf{\hat i} + (x^2 - yz)\,\mathbf{\hat j} + z \,\mathbf{\hat k}. \end{align*}\]
Encuentra el rizo de\(\vecs{F} = \langle \sin x \, \cos z, \, \sin y \, \sin z, \, \cos x \, \cos y \rangle \) en el punto\(\left(0, \dfrac{\pi}{2}, \dfrac{\pi}{2} \right)\).
- Pista
-
Encuentra el determinante de la matriz\(\vecs \nabla \times \vecs{F}\).
- Contestar
-
\(-\hat{i}\)
Encuentra el rizo de\(\vecs{F} = \langle P,Q \rangle = \langle y,0\rangle\).
Solución
Observe que este campo vectorial consiste en vectores que son todos paralelos. De hecho, cada vector en el campo es paralelo al eje x. Este hecho podría llevarnos a la conclusión de que el campo no tiene giro y que el rizo es cero. Para probar esta teoría, tenga en cuenta que
\[\text{curl}\, \vecs{F} = (Q_x - P_y)\,\mathbf{\hat k} = -\,\mathbf{\hat k} \neq \vecs 0. \nonumber \]
Por lo tanto, este campo vectorial sí tiene giro. Para ver por qué, imagina colocar una rueda de paletas en cualquier punto del primer cuadrante (Figura\(\PageIndex{6}\)). Las mayores magnitudes de los vectores en la parte superior de la rueda hacen que la rueda gire. La rueda gira en sentido horario (negativo), haciendo que el coeficiente del rizo sea negativo.
Tenga en cuenta que si\(\vecs{F} = \langle P,Q\rangle\) es un campo vectorial en un plano, entonces\(\text{curl}\, \vecs{F} \cdot \mathbf{\hat k} = (Q_x - P_y)\,\mathbf{\hat k} \cdot \mathbf{\hat k} = Q_x - P_y\). Por lo tanto, la forma de circulación del teorema de Green a veces se escribe como
\[\oint_C \vecs{F} \cdot d\vecs{r} = \iint_D \text{curl}\, \vecs F \cdot \,\mathbf{\hat k}\,dA, \nonumber \]
donde\(C\) es una curva cerrada simple y\(D\) es la región encerrada por\(C\). Por lo tanto, la forma de circulación del teorema de Green se puede escribir en términos del rizo. Si pensamos en curl como una especie de derivado, entonces el teorema de Green dice que el “derivado” de\(\vecs{F}\) en una región puede traducirse en una línea integral de\(\vecs{F}\) a lo largo del límite de la región. Esto es análogo al Teorema Fundamental del Cálculo, en el que la derivada de una función\(f\) en segmento de línea\([a,b]\) puede traducirse en una declaración\(f\) sobre en el límite de\([a,b]\). Usando curl, podemos ver que la forma de circulación del teorema de Green es un análogo de mayor dimensión del Teorema Fundamental del Cálculo.
Ahora podemos usar lo que hemos aprendido sobre el curl para mostrar que los campos gravitacionales no tienen “giro”. Supongamos que hay un objeto en el origen con masa\(m_1\) en el origen y un objeto con masa\(m_2\). Recordemos que la fuerza gravitacional que el objeto 1 ejerce sobre el objeto 2 viene dada por campo
\[ \vecs{F}(x,y,z) = - Gm_1m_2 \left\langle \dfrac{x}{(x^2 + y^2 + z^2 )^{3/2}}, \dfrac{y}{(x^2 + y^2 + z^2 )^{3/2}}, \dfrac{z}{(x^2 + y^2 + z^2 )^{3/2}}\right\rangle. \nonumber \]
Demostrar que un campo gravitacional no tiene giro.
Solución
Para demostrar que no\(\vecs{F}\) tiene giro, calculamos su rizo. Let
- \(P(x,y,z) = \dfrac{x}{(x^2 + y^2 + z^2 )^{3/2}}\),
- \(Q(x,y,z) = \dfrac{y}{(x^2 + y^2 + z^2 )^{3/2}}\), y
- \(R(x,y,z) = \dfrac{z}{(x^2 + y^2 + z^2 )^{3/2}}\).
Entonces,
\ [\ begin {align*}\ text {curl}\,\ vecs {F} &= - GM_1m_2 [(R_y - Q_z)\ mathbf {\ hat i} + (P_z - R_x)\ mathbf {\ hat j} + (Q_x - P_y)\ mathbf {\ hat k}]\\ [4pt]
&= - gm= _1m_2\ begin {pmatrix}\ left (\ dfrac {-3yz} {(x^2 + y^2 + z^2) ^ {5/2}} -\ izquierda (\ dfrac {-3yz} {(x^2 + y^2 + z^2) ^ {5/2}}\ derecha)\ derecha)\ mathbf {\ hat i}\ nonumber\\ [4pt]
+\ izquierda (\ dfrac {-3xz} {(x^2 + y^2 + z^2) ^ {5/2}} -\ izquierda (\ dfrac {-3xz} {(x^2 + y^2 + z^2) ^ {5/2}}\ derecha)\ derecha)\ mathbf {\ sombrero}\ nonumber\\ [4pt]
+\ izquierda (\ dfrac {-3xy} {(x^2 + y^2 + z^2) ^ {5/2}} -\ izquierda (\ dfrac {-3xy} {(x^2 + y^2 + z^2) ^ {5/2}}\ derecha)\ derecha)\ mathbf {\ hat k}\ end {pmatrix}\\ [4pt]
&=\ vecs 0. \ end {alinear*}\]
Dado que el rizo del campo gravitacional es cero, el campo no tiene giro.
El campo\(\vecs{v}(x,y) = \langle - \dfrac{y}{x^2+y^2}, \dfrac{x}{x^2+y^2} \rangle \) modela el flujo de un fluido. Demuestre que si deja caer una hoja en este fluido, a medida que la hoja se mueve con el tiempo, la hoja no gira.
- Pista
-
Calcula el rizo.
- Contestar
-
\(\text{curl}\, \vecs{v} = \vecs 0\)
Usando Divergencia y Curl
Ahora que entendemos los conceptos básicos de divergencia y rizo, podemos discutir sus propiedades y establecer relaciones entre ellos y los campos vectoriales conservadores.
Si\(\vecs{F}\) es un campo vectorial en\(\mathbb{R}^3\) entonces el curl de también\(\vecs{F}\) es un campo vectorial en\(\mathbb{R}^3\). Por lo tanto, podemos tomar la divergencia de un rizo. El siguiente teorema dice que el resultado siempre es cero. Este resultado es útil porque nos da una manera de mostrar que algunos campos vectoriales no son el rizo de ningún otro campo. Para dar a este resultado una interpretación física, recordemos que la divergencia de un campo de velocidad\(\vecs{v}\) en un punto\(P\) mide la tendencia del fluido correspondiente a fluir fuera de él\(P\). Ya que\(\text{div}(\text{curl}\,\vecs v) = 0\), la tasa neta de flujo en campo vectorial\(\text{curl}\;\vecs v\) en cualquier punto es cero. Tomar el rizo del campo vectorial\(\vecs{F}\) elimina cualquier divergencia que estuviera presente en\(\vecs{F}\).
Let\(\vecs{F} = \langle P,Q,R \rangle \) Ser un campo vectorial en\(\mathbb{R}^3\) tal que todas las funciones componentes tengan derivadas parciales continuas de segundo orden. Entonces,
\[\text{div}(\text{curl}\, \vecs{F}) = \vecs\nabla \cdot (\vecs \nabla \times \vecs F) = 0. \nonumber \]
Por las definiciones de divergencia y rizo, y por el teorema de Clairaut,
\[\begin{align*} \text{div}(\text{curl}\, \vecs{F}) = \text{div}[(R_y - Q_z)\,\mathbf{\hat i} + (P_z - R_x)\,\mathbf{\hat j} + (Q_x - P_y)\,\mathbf{\hat k}] \\ = R_{yx} - Q_{xz} + P_{yz} - R_{yx} + Q_{zx} - P_{zy}\\ = 0. \end{align*}\]
\(\Box\)
Mostrar que no\(\vecs{F}(x,y,z) = e^x\,\mathbf{\hat i}+ yz\,\mathbf{\hat j} + xz^2\,\mathbf{\hat k}\) es el rizo de otro campo vectorial. Es decir, mostrar que no hay otro vector\(\vecs{G}\) con\(\text{curl} \, \vecs G = \vecs F\).
Solución
Observe que el dominio de\(\vecs{F}\) es todo\(\mathbb{R}^3\) y los parciales de segundo orden de\(\vecs{F}\) son todos continuos. Por lo tanto, podemos aplicar el teorema anterior a\(\vecs{F}\).
La divergencia de\(\vecs{F}\) es\(e^x + z + 2xz\). Si\(\vecs{F}\) fueran el rizo del campo vectorial\(\vecs{G}\), entonces\(\text{div}\, \vecs F = \text{div}(\text{curl} \,\vecs G) = 0\). Pero, la divergencia de no\(\vecs{F}\) es cero, y por lo tanto no\(\vecs{F}\) es el rizo de ningún otro campo vectorial.
¿Es posible que\(\vecs G(x,y,z) = \langle \sin x, \, \cos y, \, \sin (xyz)\rangle \) sea el rizo de un campo vectorial?
- Pista
-
Encuentra la divergencia de\(\vecs{G}\).
- Contestar
-
No.
Con los dos teoremas siguientes, mostramos que si\(\vecs{F}\) es un campo vectorial conservador entonces su curl es cero, y si el dominio de\(\vecs{F}\) está simplemente conectado entonces lo contrario también es cierto. Esto nos da otra manera de probar si un campo vectorial es conservador.
Si\(\vecs{F} = \langle P,Q,R\rangle\) es conservador, entonces\(\text{curl} \, \vecs{F} = \vecs 0\).
Dado que los campos vectoriales conservadores satisfacen la propiedad de partidos cruzados, todos los parciales cruzados de\(\vecs F\) son iguales. Por lo tanto,
\[\begin{align*} \text{curl}\, \vecs{F} &= (R_y - Q_z)\,\mathbf{\hat i} + (P_z - R_x)\,\mathbf{\hat j} + (Q_x - P_y)\,\mathbf{\hat k} \\[4pt] &= \vecs 0. \end{align*}\]
\(\Box\)
El mismo teorema es cierto para los campos vectoriales en un plano.
Dado que un campo vectorial conservador es el gradiente de una función escalar, el teorema anterior dice que\(\text{curl}\, (\vecs \nabla f) = \vecs 0\) para cualquier función escalar\(f\). En términos de nuestra notación de rizo,\(\vecs \nabla \times \vecs \nabla (f) = \vecs 0\). Esta ecuación tiene sentido porque el producto cruzado de un vector consigo mismo es siempre el vector cero. A veces la ecuación\(\vecs \nabla \times \vecs \nabla (f) = \vecs 0\) se simplifica como\(\vecs \nabla \times \vecs \nabla = \vecs 0\).
Let\(\vecs{F} = \langle P,Q,R\rangle\) Ser un campo vectorial en el espacio en un dominio simplemente conectado. Si\(\text{curl}\;\vecs F = \vecs 0\), entonces\(\vecs{F}\) es conservador.
Ya que\(\text{curl}\, \vecs F = \vecs 0\), tenemos eso\(R_y = Q_z, \, P_z = R_x\), y\(Q_x = P_y\). Por lo tanto,\(\vecs{F}\) satisface la propiedad transversal parcial en un dominio simplemente conectado, y la Propiedad Cruz-Parcial de Campos Conservadores implica que\(\vecs{F}\) es conservadora.
\(\Box\)
El mismo teorema también es cierto en un plano. Por lo tanto, si\(\vecs{F}\) es un campo vectorial en un plano o en el espacio y el dominio simplemente está conectado, entonces\(\vecs{F}\) es conservador si y solo si\(\text{curl}\, \vecs F = \vecs 0\).
Usa el rizo para determinar si\(\vecs{F}(x,y,z) = \langle yz, xz, xy\rangle\) es conservador.
Solución
Tenga en cuenta que el dominio de\(\vecs{F}\) es todo\(\mathbb{R}^3\) lo cual está simplemente conectado (Figura\(\PageIndex{7}\)). Por lo tanto, podemos probar si\(\vecs{F}\) es conservador calculando su rizo.
El rizo de\(\vecs{F}\) es
\[\left(\dfrac{\partial}{\partial y}xy - \dfrac{\partial}{\partial z} xz \right) \,\mathbf{\hat i} + \left(\dfrac{\partial}{\partial y}yz - \dfrac{\partial}{\partial z} xy \right) \,\mathbf{\hat j} + \left(\dfrac{\partial}{\partial y}xz - \dfrac{\partial}{\partial z} yz \right)\,\mathbf{\hat k}= (x - x)\,\mathbf{\hat i} + (y - y)\,\mathbf{\hat j} + (z - z)\,\mathbf{\hat k} = \vecs 0. \nonumber \]
Así,\(\vecs{F}\) es conservador.
Hemos visto que el rizo de un gradiente es cero. ¿Cuál es la divergencia de un gradiente? Si\(f\) es una función de dos variables, entonces\(\text{div}(\vecs \nabla f) = \vecs \nabla \cdot (\vecs \nabla f) = f_{xx} + f_{yy}\). Abreviamos este “producto de doble punto” como\(\vecs \nabla^2\). Este operador se llama operador Laplace, y en esta notación se convierte la ecuación de Laplace\(\vecs \nabla^2 f = 0\). Por lo tanto, una función armónica es una función que se convierte en cero después de tomar la divergencia de un gradiente.
Del mismo modo, si\(f\) es una función de tres variables entonces
\[\text{div}(\vecs \nabla f) = \vecs \nabla \cdot (\vecs \nabla f) = f_{xx} + f_{yy} + f_{zz}. \nonumber \]
Usando esta notación obtenemos la ecuación de Laplace para funciones armónicas de tres variables:
\[\vecs \nabla^2 f = 0. \nonumber \]
Las funciones armónicas surgen en muchas aplicaciones. Por ejemplo, la función potencial de un campo electrostático en una región del espacio que no tiene carga estática es armónica.
¿Es posible que\(f(x,y) = x^2 + x - y\) sea la función potencial de un campo electrostático que se ubica en una región\(\mathbb{R}^2\) libre de carga estática?
Solución
Si\(f\) fuera tal función potencial, entonces\(f\) sería armónico. Tenga en cuenta que\(f_{xx} = 2\) y\(f_{yy} = 0\), y así\(f_{xx} + f_{yy} \neq 0\). Por lo tanto, no\(f\) es armónico y\(f\) no puede representar un potencial electrostático.
¿Es posible que la función\(f(x,y) = x^2 - y^2 + x\) sea la función potencial de un campo electrostático ubicado en una región\(\mathbb{R}^2\) libre de carga estática?
- Pista
-
Determinar si la función es armónica.
- Contestar
-
Sí.
Conceptos clave
- La divergencia de un campo vectorial es una función escalar. La divergencia mide el “flujo de salida” de un campo vectorial. Si\(\vecs{v}\) es el campo de velocidad de un fluido, entonces la divergencia de\(\vecs{v}\) en un punto es la salida del fluido menos la entrada en el punto.
- El rizo de un campo vectorial es un campo vectorial. El rizo de un campo vectorial en el punto\(P\) mide la tendencia de las partículas\(P\) a girar alrededor del eje que apunta en la dirección del rizo en\(P\).
- Un campo vectorial con un dominio simplemente conectado es conservador si y solo si su curl es cero.
Ecuaciones Clave
- Curl
\[\vecs \nabla \times \vecs{F} = (R_y - Q_z)\,\mathbf{\hat i} + (P_z - R_x)\,\mathbf{\hat j} + (Q_x - P_y)\,\mathbf{\hat k} \nonumber \]
- Divergencia
\[\vecs \nabla \cdot \vecs{F} = P_x + Q_y + R_z\nonumber \]
- La divergencia del rizo es cero
\[\vecs \nabla \cdot (\vecs \nabla \times \vecs F) = 0\nonumber \]
- Curl de un gradiente es el vector cero
\[\vecs \nabla \times (\vecs \nabla f) = 0 \nonumber \]
Glosario
- rizo
- el rizo del campo vectorial\(\vecs{F}=⟨P,Q,R⟩\), denotado\(\vecs ∇× \vecs{F}\) es el “determinante” de la matriz\[\begin{vmatrix} \mathbf{\hat i} & \mathbf{\hat j} & \mathbf{\hat k} \\ \dfrac{\partial}{\partial x} & \dfrac{\partial}{\partial y} & \dfrac{\partial}{\partial z} \\ P & Q & R \end{vmatrix}. \nonumber \] y viene dado por la expresión\((R_y−Q_z)\,\mathbf{\hat i} +(P_z−R_x)\,\mathbf{\hat j} +(Q_x−P_y)\,\mathbf{\hat k} \); mide la tendencia de las partículas en un punto a girar alrededor del eje que apunta en la dirección del rizo en el punto
- divergencia
- la divergencia de un campo vectorial\(\vecs{F}=⟨P,Q,R⟩\), denotado\(\vecs ∇× \vecs{F}\), es\(P_x+Q_y+R_z\); mide el “flujo de salida” de un campo vectorial



Una aplicación para la divergencia ocurre en la física, cuando se trabaja con campos magnéticos. Un campo magnético es un campo vectorial que modela la influencia de corrientes eléctricas y materiales magnéticos. Los físicos utilizan la divergencia en la ley de Gauss para el magnetismo, que establece que si\(\vecs{B}\) es un campo magnético, entonces\(\vecs \nabla \cdot \vecs{B} = 0\); en otras palabras, la divergencia de un campo magnético es cero.
Ejemplo\(\PageIndex{2}\): Determining Whether a Field Is Magnetic
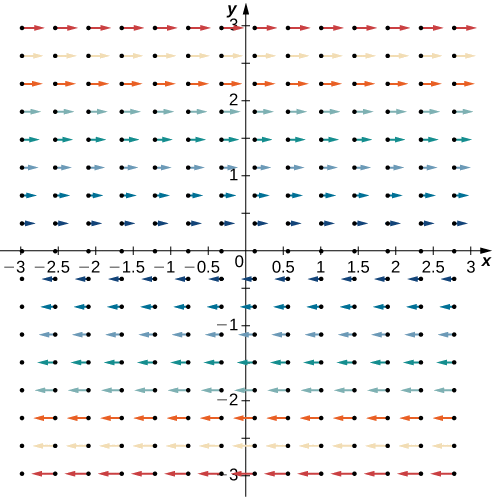
¿Es posible\(\vecs{F} (x,y) = \langle x^2 y, \, y - xy^2 \rangle \) que sea un campo magnético?
Solución
Si\(\vecs{F}\) fueran magnéticos, entonces su divergencia sería cero. La divergencia de\(\vecs{F}\) es
\[\dfrac{\partial}{\partial x} (x^2y) + \dfrac{\partial}{\partial y} (y - xy^2) = 2 xy + 1 - 2 xy = 1 \nonumber \]
y por lo tanto\(\vecs{F}\) no puede modelar un campo magnético (Figura\(\PageIndex{3}\)).