3.5: Ejercicios

Última actualización
Guardar como PDF

Page ID: 112944

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

1. Enumere los elementos del conjunto “Las letras de la palabra Mississippi”.

2. Enumere los elementos del conjunto “Meses del año”.

3. Escribe una descripción verbal del conjunto {3, 6, 9}.

4. Escribir una descripción verbal del conjunto {a, e, i, o, u}.

5. ¿Es {1, 3, 5} un subconjunto del conjunto de enteros impares?

6. ¿Es {A, B, C} un subconjunto del conjunto de letras del alfabeto?

Para los problemas 7-12, considere los conjuntos a continuación, e indique si cada enunciado es verdadero o falso.

$A$= {1, 2, 3, 4, 5}$B$ = {1, 3, 5}$C$ = {4, 6}$U$ = {números del 0 al 10}

7. $3 ∊ B$

8. $5 ∊ C$

9. $B ⊂ A$

10. $C ⊂ A$

11. $C ⊂ B$

12. $C ⊂ D$

Usando los conjuntos de arriba, y tratando$U$ como el conjunto Universal, encuentre cada uno de los siguientes:

13. $A ⋃ B$

14. $A ⋃ C$

15. $A ⋂ C$

16. $B ⋂ C$

17. $A^c$

18. $B^c$

Sea D = {b, a, c, k}, E = {t, a, s, k}, F = {b, a, t, h}. Usando estos conjuntos, encuentre lo siguiente:

19. $D^c ⋂ E$

20. $F^c ⋂ D$

21. $(D ⋂ E) ⋃ F$

22. $D ⋂ (E ⋃ F)$

23. $(F ⋂ E)^c ⋂ D$

24. $(D ⋃ E)^c ⋂ F$

Cree un diagrama de Venn para ilustrar cada uno de los siguientes:

25. $(F ⋂ E) ⋃ D$

26. $(D ⋃ E)^c ⋂ F$

27. $(F^c ⋂ E^c) ⋂ D$

28. $(D ⋃ E) ⋃ F$

Escribe una expresión para la región sombreada.

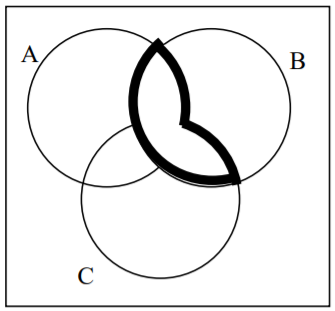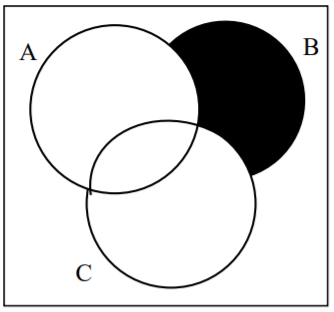
29. $clipboard_e009bdf9d0a715e5328783f380d149e39.png$ 30. $clipboard_e729b20fbd0035fd4b92724990f64ec2a.png$

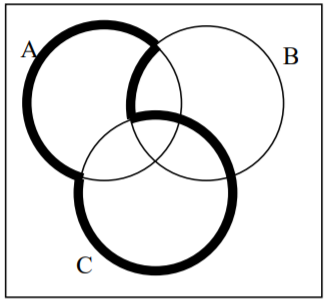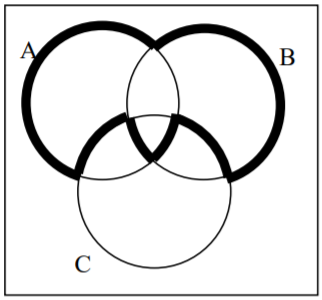
31. $clipboard_e09e1d68bdfa6445007f9a1539bbe3151.png$ 32. $clipboard_e5db31d5c8ae768a37aaf4d22da9b3cae.png$

Sea A = {1, 2, 3, 4, 5} B = {1, 3, 5} C = {4, 6}. Encuentra la cardinalidad del conjunto dado.

33. $\text{n}(A)$

34. $\text{n}(B)$

35. $\text{n}(A ⋃ C)$

36. $\text{n}(A ⋂ C)$

El diagrama de Venn aquí muestra la cardinalidad de cada conjunto. Usa esto en 37-40 para encontrar la cardinalidad del conjunto dado.

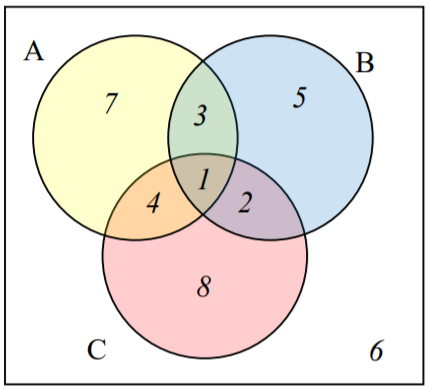
$clipboard_e47bdb843918155d8aaa2b02aba2dfaaa.png$

37. $\text{n}(A ⋂ C)$

38. $\text{n}(B ⋃ C)$

39. $\text{n}(A ⋂ B ⋂ C^c)$

40. $\text{n}(A ⋂ B^c ⋂ C)$

41. Si$\text{n}(G) = 20$,$\text{n}(H) = 30$,$\text{n}(G ⋂ H) = 5$, encuentra$\text{n}(G ⋃ H)$.

42. Si$\text{n}(G) = 5$,$\text{n}(H) = 8$,$\text{n}(G ⋂ H) = 4$, encuentra$\text{n}(G ⋃ H)$.

43. Se realizó una encuesta preguntando si ven películas en casa desde Netflix, Redbox o una tienda de videos. Usa los resultados para determinar cuántas personas usan Redbox.

52 solo usa Netflix
62 solo usa Redbox
24 solo usa una tienda de videos
16 usa solo una tienda de videos y Redbox
48 usan solo Netflix y Redbox
30 usa solo una tienda de videos y Netflix
10 usan los tres
25 no usan ninguno de estos

44. Una encuesta preguntó a los compradores si el color, el tamaño o la marca influyeron en su elección del teléfono celular. Los resultados están a continuación. ¿Cuántas personas fueron influenciadas por la marca?

5 solo dicho color
8 solo dicho tamaño
16 solo dicha marca
20 dicho solo color y tamaño
42 dijo que sólo el color y la marca
53 dijo que sólo el tamaño y la marca
102 dijo los tres
20 dijo ninguno de estos

45. Usa la información dada para completar un diagrama de Venn, luego determinar: a) cuántos estudiantes han visto exactamente una de estas películas, y b) cuántos habían visto solo Star Wars.

18 habían visto The Matrix (M)
24 habían visto Star Wars (SW)
20 habían visto Señor de los Anillos (LoTR)
10 habían visto M y SW
14 habían visto LoTR y SW
12 habían visto M y LotR
6 habían visto los tres

46. Una encuesta preguntó a las personas qué modos de transporte alternativos utilizan. Usando los datos para completar un diagrama de Venn, luego determinar: a) qué porcentaje de personas solo viajan en autobús, y b) cuántas personas no utilizan ningún transporte alternativo.

30% usa el autobús
20% andar en bicicleta
25% a pie
5% usa el autobús y anda en bicicleta
10% andar en bicicleta y caminar
12% usa el autobús y camina
2% usa los tres

Search

Text Color

Text Size

Margin Size

Font Type