3.4: Cardenalidad
- Page ID
- 112939
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Muchas veces nos interesa el número de ítems en un conjunto o subconjunto. A esto se le llama la cardinalidad del conjunto.
El número de elementos en un conjunto es la cardinalidad de ese conjunto.
La cardinalidad del conjunto a menudo\(A\) se anota como\(|A|\) o n\((A)\).
Dejar\(A\) = {1, 2, 3, 4, 5, 6} y\(B\) = {2, 4, 6, 8}. ¿De qué es la cardinalidad\(B\)? \(A ⋃ B\),\(A ⋂ B\)?
Solución
La cardinalidad de\(B\) es 4, ya que hay 4 elementos en el conjunto.
La cardinalidad de\(A ⋃ B\) es 7, ya que\(A ⋃ B\) = {1, 2, 3, 4, 5, 6, 8}, que contiene 7 elementos.
La cardinalidad de\(A ⋂ B\) es 3, ya que\(A ⋂ B\) = {2, 4, 6}, que contiene 3 elementos.
¿Cuál es la cardinalidad de\(P\) = el conjunto de nombres ingleses para los meses del año?
Solución
La cardinalidad de este conjunto es de 12, ya que hay 12 meses en el año.
A veces nos puede interesar la cardinalidad de la unión o intersección de conjuntos, pero no conocer los elementos reales de cada conjunto. Esto es común en la topografía.
Una encuesta pregunta a 200 personas “¿Qué bebida tomas por la mañana?”, y ofrece opciones
- Solo té
- Solo café
- Tanto el café como el té
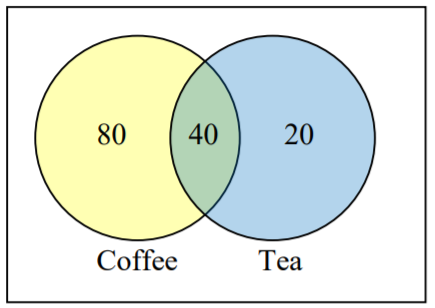
Supongamos que 20 reportan solo té, 80 reportan solo café, 40 reportan ambos. ¿Cuántas personas toman té por la mañana? ¿Cuántas personas no beben ni té ni café?
Solución
Esta pregunta se puede responder más fácilmente creando un diagrama de Venn. Podemos ver que podemos encontrar a las personas que toman té agregando a quienes solo beben té a quienes beben tanto: 60 personas.
También podemos ver que los que no beben ni son los que no están contenidos en ninguna de las otras tres agrupaciones, así podemos contarlos restando de la cardinalidad del conjunto universal, 200. 200 — 20 — 80 — 40 = 60 personas que no beben ninguna.
Una encuesta pregunta: ¿Qué servicios en línea has utilizado en el último mes?
- Haber utilizado ambos
Los resultados muestran que\(40\%\) los encuestados han usado Twitter,\(70\%\) han usado Facebook, y\(20\%\) han utilizado ambos. ¿Cuántas personas no han usado ni Twitter ni Facebook?
Solución
\(T\)Sea el conjunto de todas las personas que han usado Twitter, y\(F\) ser el conjunto de todas las personas que han usado Facebook. Observe que si bien la cardinalidad de\(F\) es\(70\%\) y la cardinalidad de\(T\) es\(40\%\), la cardinalidad de no\(F ⋃ T\) es simplemente\(70\% + 40\%\), ya que eso contaría a quienes utilizan ambos servicios dos veces. Para encontrar la cardinalidad de\(F ⋃ T\), podemos sumar la cardinalidad de\(F\) y la cardinalidad de\(T\), luego restar los de la intersección que hemos contado dos veces. En símbolos,
\(\text{n}(F ⋃ T) = \text{n}(F) + \text{n}(T) – \text{n}(F ⋂ T)\)
\(\text{n}(F ⋃ T) = 70\% + 40\% – 20\% = 90\%\)
Ahora bien, para saber cuántas personas no han utilizado ninguno de los dos servicios, estamos buscando la cardinalidad de\((F ⋃ T)^c\). Dado que el conjunto universal contiene\(100\%\) de personas y la cardinalidad de\(F ⋃ T = 90\%\), la cardinalidad de\((F ⋃ T)^c\) debe ser la otra\(10\%\).
El ejemplo anterior ilustraba dos propiedades importantes.
\(\text{n}(A ⋃ B) = \text{n}(A) + \text{n}(B) – \text{n}(A ⋂ B)\)
\(\text{n}(A^c) = \text{n}(U) – \text{n}(A)\)
Observe que la primera propiedad también se puede escribir en forma equivalente resolviendo para la cardinalidad de la intersección:
\(\text{n}(A ⋂ B) = \text{n}(A) + \text{n}(B) – \text{n}(A ⋃ B)\)
Se encuestó a cincuenta estudiantes, y se les preguntó si estaban cursando un curso de ciencias sociales (SS), humanidades (HM) o ciencias naturales (NS) al trimestre siguiente.
- 21 estaban tomando un curso de SS
- 26 estaban tomando un curso de HM
- 19 estaban tomando un curso de NS
- 9 estaban tomando SS y HM
- 7 estaban tomando SS y NS
- 10 estaban tomando HM y NS
- 3 estaban tomando los tres
- 7 estaban tomando ninguno
¿Cuántos alumnos solo están tomando un curso de SS?
Solución
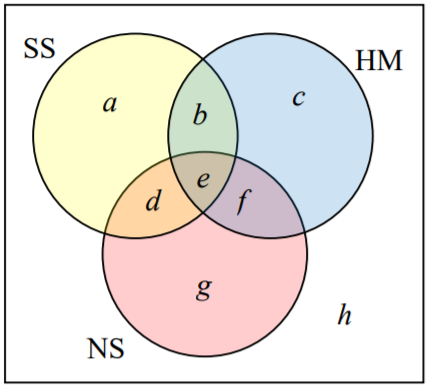Podría ser de ayuda mirar un diagrama de Venn. A partir de los datos dados, sabemos que hay 3 estudiantes en región\(e\) y 7 estudiantes en región\(h\).
Ya que 7 alumnos estaban tomando un curso de SS y NS, eso lo sabemos\(\text{n}(d) + \text{n}(e) = 7\). Como sabemos que hay 3 estudiantes en la región 3, debe haber 7 — 3 = 4 estudiantes en la región\(d\).
De igual manera, ya que hay 10 alumnos cursando HM y NS, lo que incluye regiones\(e\) y\(f\), debe haber 10 — 3 = 7 alumnos en región\(f\).
Ya que 9 estudiantes estaban tomando SS y HM, debe haber 9 — 3 = 6 estudiantes en la región\(b\).
Ahora, sabemos que 21 alumnos estaban tomando un curso de SS. Esto incluye a estudiantes de regiones\(a\),\(b\),\(d\), y\(e\). Dado que conocemos el número de estudiantes en todos menos región\(a\), podemos determinar que 21 — 6 — 4 — 3 = 8 estudiantes están en región\(a\).
8 alumnos están tomando solamente un curso de SS.
Ciento cincuenta personas fueron encuestadas y se les preguntó si creían en ovnis, fantasmas y Bigfoot.
- 43 cree en los ovnis
- 44 cree en fantasmas
- 25 cree en Bigfoot
- 10 cree en ovnis y fantasmas
- 8 cree en fantasmas y Bigfoot
- 5 cree en ovnis y Bigfoot
- 2 creyeron en los tres
¿Cuántas personas encuestadas creían en al menos una de estas cosas?
1. Hay varias respuestas: El conjunto de todos los números impares menores a 10. El conjunto de todos los números impares. El conjunto de todos los enteros. El conjunto de todos los números reales.
2. \(A ⋃ C\)= {rojo, naranja, amarillo, verde, azul púrpura}\(B^c ⋂ A\) = {verde, azul}
3. \(A ⋃ B ⋂ C^c\)
4. Comenzando por la intersección de los tres círculos, trabajamos nuestra salida. Ya que 10 personas creen en ovnis y fantasmas, y 2 creen en los tres, eso deja 8 que creen solo en ovnis y fantasmas. Trabajamos nuestra salida, llenando todas las regiones. Una vez que tenemos, podemos sumar todas esas regiones, consiguiendo 91 personas en la unión de los tres conjuntos. Esto deja 150 — 91 = 59 que no creen en ninguno.
