5.9: El teorema de Pitágoras

Última actualización
Guardar como PDF

Page ID: 113434

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Pitágoras fue un matemático y filósofo griego, nacido en la isla de Samos (ca. 582 a.C.). Fundó varias escuelas, una en particular en una ciudad del sur de Italia llamada Crotone, cuyos miembros finalmente se conocieron como los pitagóricos. El círculo íntimo de la escuela, el Mathematikoi, vivía en la escuela, se libraba de todas las posesiones personales, eran vegetarianos y observaban un estricto voto de silencio. Estudiaron matemáticas, filosofía y música, y sostenían la creencia de que los números constituyen la verdadera naturaleza de las cosas, dando a los números una cualidad mística o incluso espiritual.

Hoy no se sabe nada de los escritos de Pitágoras, quizás por el secreto y el silencio de la sociedad pitagórica. Sin embargo, uno de los teoremas más famosos de todas las matemáticas sí lleva su nombre, el Teorema de Pitágoras.

Antes de revelar los contenidos del Teorema de Pitágoras, hacemos una pausa para proporcionar la definición de un triángulo rectángulo y sus partes constituyentes.

Triángulo recto

Un triángulo con un ángulo recto (90 ^◦) se denomina triángulo rectángulo. En la siguiente figura, el ángulo recto está marcado con un pequeño cuadrado.

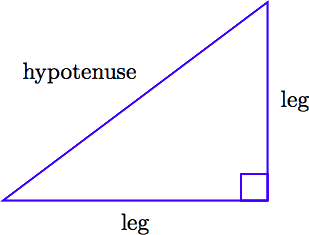
$imageedit_2_4590690964.png$

El lado del triángulo que está directamente opuesto al ángulo recto se llama hipotenusa. Los lados del triángulo que incluyen el ángulo recto se denominan patas del triángulo rectángulo.

Ahora podemos exponer uno de los teoremas más antiguos de las matemáticas, el Teorema de Pitágoras.

Teorema de Pitágoras

Dejar$c$ representar la longitud de la hipotenusa de un triángulo rectángulo, y dejar que a y b representan las longitudes de sus patas, como se muestra en la imagen que sigue.

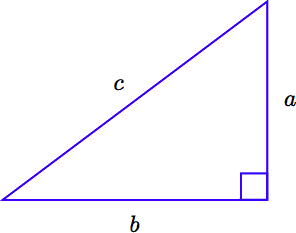
$imageedit_6_3162970942.png$

La relación que involucra las piernas y la hipotenusa del triángulo rectángulo, dada por

\[a^2 + b^2 = c^2,\nonumber \]

se llama Teorema de Pitágoras.

Aquí hay dos observaciones importantes.

Observaciones respecto a la hipotenusa

Dos hechos importantes respecto a la hipotenusa del triángulo rectángulo son:

La hipotenusa es el lado más largo del triángulo y se encuentra directamente opuesto al ángulo recto.
En la ecuación pitagórica$a^2 + b^2 = c^2$, la hipotenusa se encuentra por sí misma en un lado de la ecuación.

El Teorema de Pitágoras sólo se puede aplicar a los triángulos rectos.

Veamos una sencilla aplicación del Teorema de Pitágoras.

Ejemplo 1

Las patas de un triángulo rectángulo miden 3 y 4 metros, respectivamente. Encuentra la longitud de la hipotenusa.

Solución

Sigamos los Requisitos para las soluciones de problemas de Word.

1. Configura un Diccionario de Variables. Que c represente la longitud de la hipotenusa, como se muestra en el siguiente boceto.

2. Configura una Ecuación. El Teorema de Pitágoras dice que

\[a^2 + b^2 = c^2.\nonumber \]

En este ejemplo, se conocen las piernas. Sustituir 4 por a y 3 por b (3 para a y 4 para b funciona igualmente bien) en la ecuación pitagórica.

\[4^2 + 3^2 = c^2\nonumber \]

3. Resuelve la Ecuación.

\[ \begin{aligned} 4^2 + 3^2 = c^2 ~ & \textcolor{red}{ \text{ The Pythagorean equation.}} \\ 16 + 9 = c^2 ~ & \textcolor{red}{ \text{ Exponents first: } 4^2 = 16 \text{ and } 3^2 = 9.} \\ 25 = c^2 ~ & \textcolor{red}{ \text{ Add: } 16+9=25.} \\ 5 = c~ & \textcolor{red}{ \text{ Take the nonnegative square root.}} \end{aligned}\nonumber \]

Técnicamente, hay dos respuestas a c ² = 25, es decir, c = −5 o c = 5. Sin embargo, c representa la hipotenusa del triángulo rectángulo y debe ser no negativa. De ahí que debemos elegir c = 5.

4. Responda a la Pregunta. La hipotenusa tiene una longitud de 5 metros.

5. Mira hacia atrás. ¿Los números satisfacen el Teorema de Pitágoras? La suma de los cuadrados de las piernas debe ser igual al cuadrado de la hipotenusa. Vamos a revisar.

\[\begin{aligned} 4^2 + 3^2 = 5^2 \\ 16 + 9 = 25 \\ 25 = 25 \end{aligned}\nonumber \]

¡Todo está bien!

Ejercicio

Las patas de un triángulo rectángulo miden 5 y 12 pies, respectivamente. Encuentra la longitud de la hipotenusa.

Responder: 13 pies

Ejemplo 2

Dado el siguiente triángulo rectángulo, encuentra la longitud del lado faltante.

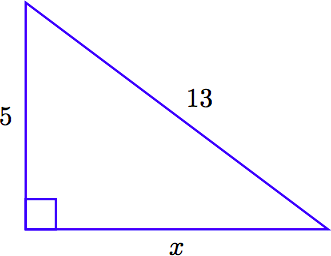
$imageedit_10_6811566794.png$

Solución

Tenga en cuenta que la hipotenusa (a través del ángulo recto) tiene una longitud 13. Esta cantidad debería estar en un lado de la ecuación pitagórica por sí sola. La suma de los cuadrados de las piernas van del otro lado. Por lo tanto,

\[5^2 + x^2 = 13^2\nonumber \]

Resuelve la ecuación para x.

\[ \begin{aligned} 25+x^2 = 169 ~ & \textcolor{red}{ \text{ Exponents first: } 5^2 = 25 \text{ and } 13^2 = 169.} \\ 25 + x^2 -25 = 169 - 25 ~ & \textcolor{red}{ \text{ Subtract 25 from both sides.}} \\ x^2 = 144 ~ & \textcolor{red}{ \text{ Simplify both sides.}} \\ x= 12 ~ & \textcolor{red}{ \text{ Take the nonnegative square root of 144.}} \end{aligned}\nonumber \]

Ejercicio

La hipotenusa de un triángulo rectángulo mide 25 centímetros. Una pata del triángulo rectángulo mide 24 centímetros. Encuentra la longitud de la pierna restante.

Responder: 7 centímetros

Los cuadrados perfectos son agradables, pero no requeridos.

Ejemplo 3

Dado el siguiente triángulo rectángulo, encuentra la longitud exacta del lado faltante.

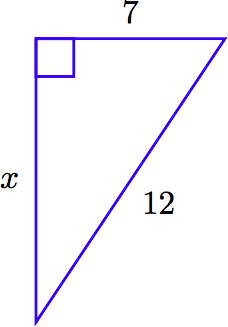
$imageedit_14_5088392393.png$

Solución

Tenga en cuenta que la hipotenusa (a través del ángulo recto) tiene una longitud 12. Esta cantidad debería estar en un lado de la ecuación pitagórica por sí sola. La suma de los cuadrados de las piernas van del otro lado. Por lo tanto,

\[x^2 + 7^2 = 12^2\nonumber \]

Resuelve la ecuación para x.

\[ \begin{aligned} x^2 + 49 = 144 ~ & \textcolor{red}{ \text{ Exponents first: } 7^2 = 49 \text{ and } 12^2 = 144.} \\ x^2 + 49-49 = 144 - 49 ~ & \textcolor{red}{ \text{ Subtract 49 from both sides.}} \\ x^2 = 95 ~ & \textcolor{red}{ \text{ Simplify both sides.}} \\ x = \sqrt{95} ~ & \textcolor{red}{ \text{ Take the nonnegative square root of 95.}} \end{aligned}\nonumber \]

De ahí que la longitud exacta del lado faltante sea$\sqrt{95}$.

Ejercicio

La hipotenusa y una pata de un triángulo rectángulo miden 9 y 7 pulgadas, respectivamente. Encuentra la longitud de la pierna restante.

Responder: Agrega textos aquí. No elimine primero este texto.

Observación Importante

Cualquier intento de usar tu calculadora para aproximar 95 en el Ejemplo 3 sería un error ya que las instrucciones pedían una respuesta exacta.

A veces se desea una respuesta aproximada, particularmente en aplicaciones.

Ejemplo 4

Ginny quiere crear un huerto en la esquina de su patio en forma de triángulo rectángulo. Ella corta dos tablas de longitud 8 pies que formarán las patas de su jardín. Encuentra la longitud de tabla que debe cortar para formar la hipotenusa de su jardín, correcta a la décima de pie más cercana.

Solución

Seguimos los Requisitos para Soluciones de Problemas de Word.

1. Configura un Diccionario de Variables. Comenzamos con un boceto etiquetado. Sea x representar la longitud de la hipotenusa desconocida.

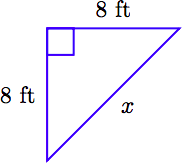
$imageedit_18_8045316766.png$

2. Configura una ecuación. La hipotenusa se aísla en un lado de la ecuación pitagórica.

\[x^2 = 8^2 + 8^2\nonumber \]

3. Resuelve la Ecuación.

\[ \begin{aligned} x^2 = 8^2 + 8^2 ~ & \textcolor{red}{ \text{ The Pythagorean equation.}} \\ x^2 = 64 + 64 ~ & \textcolor{red}{ \text{ Exponents first: } 8^2 = 64 \text{ and } 8^2 = 64.} \\ x^2 = 128 ~ & \textcolor{red}{ \text{ Add: } 64 + 64 = 128.} \\ x = \sqrt{128} ~ & \textcolor{red}{ \text{ Take the nonnegative square root.}} \end{aligned}\nonumber \]

4. Responda a la Pregunta. La longitud exacta de la hipotenusa es$\sqrt{128}$ pies, pero se nos pide encontrar la hipotenusa a la décima de pie más cercana. Usando una calculadora, encontramos una aproximación para$\sqrt{128}$.

\[\sqrt{128} \approx 11.313708499\nonumber \]

Para redondear a la décima más cercana, primero identifique los dígitos de redondeo y pruebe.

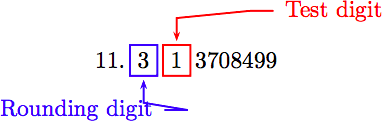
$imageedit_22_8154063398.png$

El dígito de prueba es menor a cinco. Entonces dejamos el dígito de redondeo solo y truncamos. Por lo tanto, correcta a la décima de pie más cercana, la longitud de la hipotenusa es de aproximadamente 11.3 pies.

5. Mira hacia atrás. La suma de los cuadrados de las piernas es

\[ \begin{aligned} 8^2 + 8^2 = 64 + 64 \\ = 128. \end{aligned}\nonumber \]

El cuadrado de la hipotenusa es

\[(11.3)^2 = 127.69\nonumber \]

Estos son casi lo mismo, la discrepancia debido a que redondeamos para encontrar una aproximación para la hipotenusa.

Ejercicio

Una escalera de 15 pies se apoya contra la pared de un edificio. La base de la escalera se encuentra a 5 pies de la base de la pared. ¿Qué tan alto llega a la pared la parte superior de la escalera? Redondee su respuesta a la décima de pie más cercana.

Responder: 14.1 pies

Ejercicios

En los Ejercicios 1-16, tus soluciones deben incluir un boceto bien etiquetado.

1. La longitud de una pata de un triángulo rectángulo es de 15 metros, y la longitud de la hipotenusa es de 25 metros. Encuentra la longitud exacta de la otra pierna.

2. La longitud de una pata de un triángulo rectángulo es de 7 metros, y la longitud de la hipotenusa es de 25 metros. Encuentra la longitud exacta de la otra pierna.

3. Las longitudes de dos patas de un triángulo rectángulo son de 12 metros y 16 metros. Encuentra la longitud exacta de la hipotenusa.

4. Las longitudes de dos patas de un triángulo rectángulo son de 9 metros y 12 metros. Encuentra la longitud exacta de la hipotenusa.

5. La longitud de una pata de un triángulo rectángulo es de 13 metros, y la longitud de la hipotenusa es de 22 metros. Encuentra la longitud exacta de la otra pierna.

6. La longitud de una pata de un triángulo rectángulo es de 6 metros, y la longitud de la hipotenusa es de 15 metros. Encuentra la longitud exacta de la otra pierna.

7. Las longitudes de dos patas de un triángulo rectángulo son de 2 metros y 21 metros. Encuentra la longitud exacta de la hipotenusa.

8. Las longitudes de dos patas de un triángulo rectángulo son de 7 metros y 8 metros. Encuentra la longitud exacta de la hipotenusa.

9. La longitud de una pata de un triángulo rectángulo es de 12 metros, y la longitud de la hipotenusa es de 19 metros. Encuentra la longitud exacta de la otra pierna.

10. La longitud de una pata de un triángulo rectángulo es de 5 metros, y la longitud de la hipotenusa es de 10 metros. Encuentra la longitud exacta de la otra pierna.

11. Las longitudes de dos patas de un triángulo rectángulo son de 6 metros y 8 metros. Encuentra la longitud exacta de la hipotenusa.

12. Las longitudes de dos patas de un triángulo rectángulo son de 5 metros y 12 metros. Encuentra la longitud exacta de la hipotenusa.

13. La longitud de una pata de un triángulo rectángulo es de 6 metros, y la longitud de la hipotenusa es de 10 metros. Encuentra la longitud exacta de la otra pierna.

14. La longitud de una pata de un triángulo rectángulo es de 9 metros, y la longitud de la hipotenusa es de 15 metros. Encuentra la longitud exacta de la otra pierna.

15. Las longitudes de dos patas de un triángulo rectángulo son de 6 metros y 22 metros. Encuentra la longitud exacta de la hipotenusa.

16. Las longitudes de dos patas de un triángulo rectángulo son de 9 metros y 19 metros. Encuentra la longitud exacta de la hipotenusa.

En los Ejercicios 17-24, tus soluciones deben incluir un boceto bien etiquetado.

17. Las longitudes de dos patas de un triángulo rectángulo son de 3 metros y 18 metros. Encuentra la longitud de la hipotenusa. Redondee su respuesta a la centésima más cercana.

18. Las longitudes de dos patas de un triángulo rectángulo son de 10 pies y 16 pies. Encuentra la longitud de la hipotenusa. Redondee su respuesta a la décima más cercana.

19. La longitud de una pata de un triángulo rectángulo es de 2 metros, y la longitud de la hipotenusa es de 17 metros. Encuentra la longitud de la otra pierna. Redondee su respuesta a la décima más cercana.

20. La longitud de una pata de un triángulo rectángulo es de 4 metros, y la longitud de la hipotenusa es de 12 metros. Encuentra la longitud de la otra pierna. Redondee su respuesta a la centésima más cercana.

21. Las longitudes de dos patas de un triángulo rectángulo son de 15 pies y 18 pies. Encuentra la longitud de la hipotenusa. Redondee su respuesta a la centésima más cercana.

22. Las longitudes de dos patas de un triángulo rectángulo son de 6 pies y 13 pies. Encuentra la longitud de la hipotenusa. Redondee su respuesta a la décima más cercana.

23. La longitud de una pata de un triángulo rectángulo es de 4 metros, y la longitud de la hipotenusa es de 8 metros. Encuentra la longitud de la otra pierna. Redondee su respuesta a la centésima más cercana.

24. La longitud de una pata de un triángulo rectángulo es de 3 metros, y la longitud de la hipotenusa es de 15 metros. Encuentra la longitud de la otra pierna. Redondee su respuesta a la décima más cercana.

25. Greta y Fritz están plantando un jardín rectangular de 13 metros por 18 metros, y lo están colocando usando una cuerda. A ellos les gustaría saber la longitud de una diagonal para asegurarse de que se forman ángulos rectos. Encuentra la longitud de una diagonal. Redondee su respuesta a la centésima más cercana. Su solución debe incluir un boceto bien etiquetado.

26. Markos y Angelina están plantando un jardín rectangular de 11 metros por 19 metros, y lo están colocando usando una cuerda. A ellos les gustaría saber la longitud de una diagonal para asegurarse de que se forman ángulos rectos. Encuentra la longitud de una diagonal. Redondee su respuesta a la décima más cercana. Su solución debe incluir un boceto bien etiquetado.

27. La base de un cable tensor de 24 metros de largo se encuentra a 10 metros de la base del poste telefónico que está anclando. ¿Qué tan alto llega el cable de tipo arriba del poste? Redondee su respuesta a la centésima más cercana. Su solución debe incluir un boceto bien etiquetado.

28. La base de un cable tipo de 30 pies de largo se encuentra a 9 pies de la base del poste telefónico que está anclando. ¿Qué tan alto llega el cable de tipo arriba del poste? Redondee su respuesta a la centésima más cercana. Su solución debe incluir un boceto bien etiquetado.

29. Sendero de Senderismo. Una ruta de senderismo corre hacia el sur durante 8 kilómetros, luego gira hacia el oeste por unos 15 kilómetros, y luego se dirige hacia el noreste por un camino directo hasta el punto de partida. ¿Cuánto dura todo el sendero?

30. Rastro Animal. Un rastro de animales corre hacia el este desde un abrevadero por 12 kilómetros, luego va hacia el norte por 5 kilómetros. Entonces el sendero gira hacia el suroeste por un camino directo de regreso al abrevadero. ¿Cuánto dura todo el sendero?

31. Ventana Superior. Una escalera de 10 pies se apoya contra la pared de una casa. ¿Qué tan cerca de la pared debe estar el fondo de la escalera para llegar a una ventana a 8 pies sobre el suelo?

32. ¿Qué tan alto? Una escalera de 10 pies se apoya contra la pared de una casa. ¿Qué tan alta será la escalera si la parte inferior de la escalera está a 4 pies de la pared? Redondee su respuesta a la décima más cercana.

RESPUESTAS

1. 20 metros

3. 20 metros

5. √315 metros

7. $\sqrt{445}$metros

9. $\sqrt{217}$metros

11. 10 metros

13. 8 metros

15. $\sqrt{520}$metros

17. 18.25 metros

19. 16.9 metros

21. 23.43 pies

23. 6.93 metros

25. 22.20 metros

27. 21.82 metros

29. 40 kilómetros

31. 6 ft.

Search

Text Color

Text Size

Margin Size

Font Type